Фильтрация шума очень важная вещь, при работе с различными датчиками. Сигнал, получаемый от них всегда приходит с шумами, и важно уметь их грамотно отфильтровать. Качественная фильтрация шума способна уменьшить погрешность и увеличить качество измерения датчика. Этим мы сегодня и займемся.
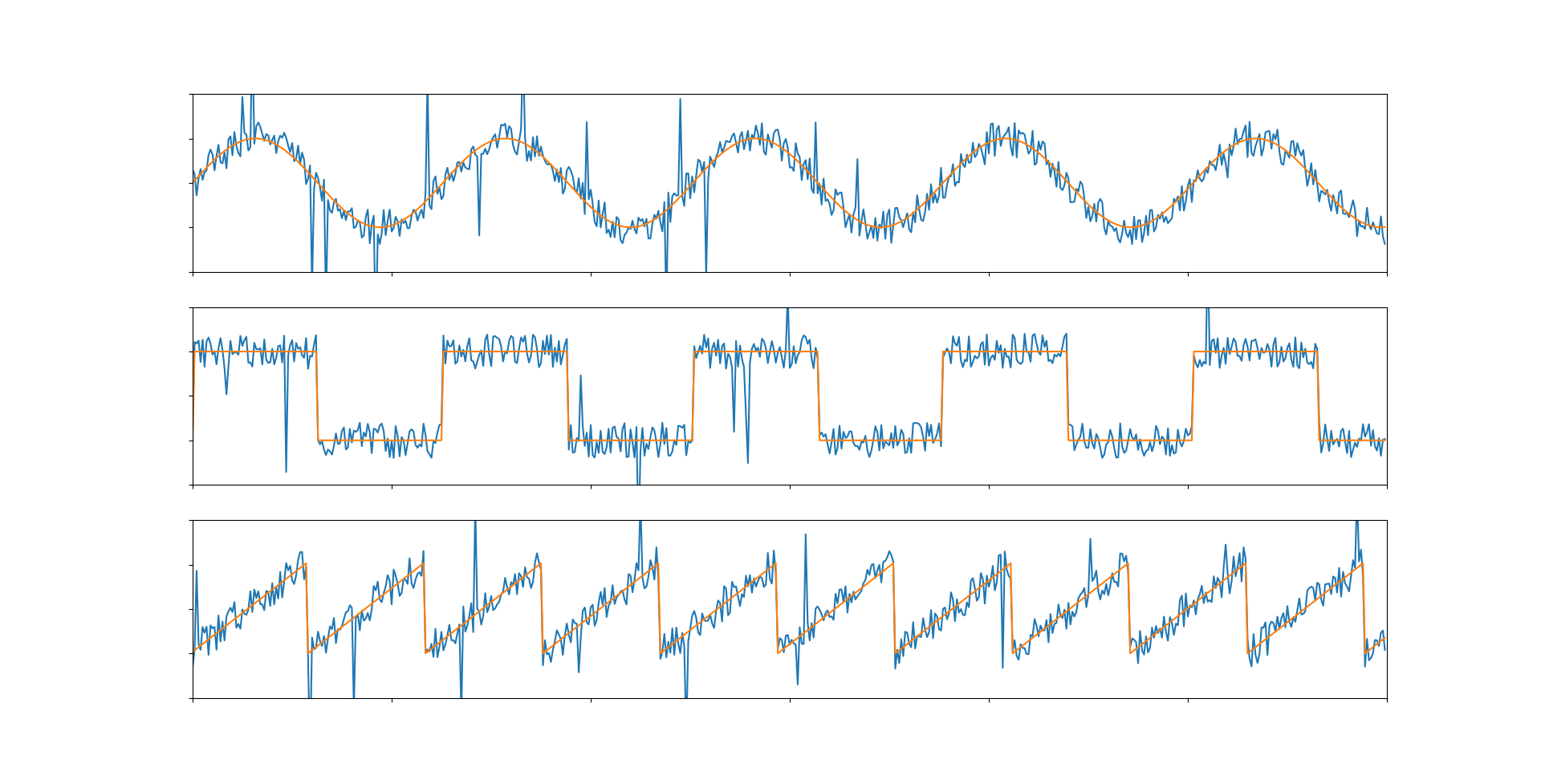
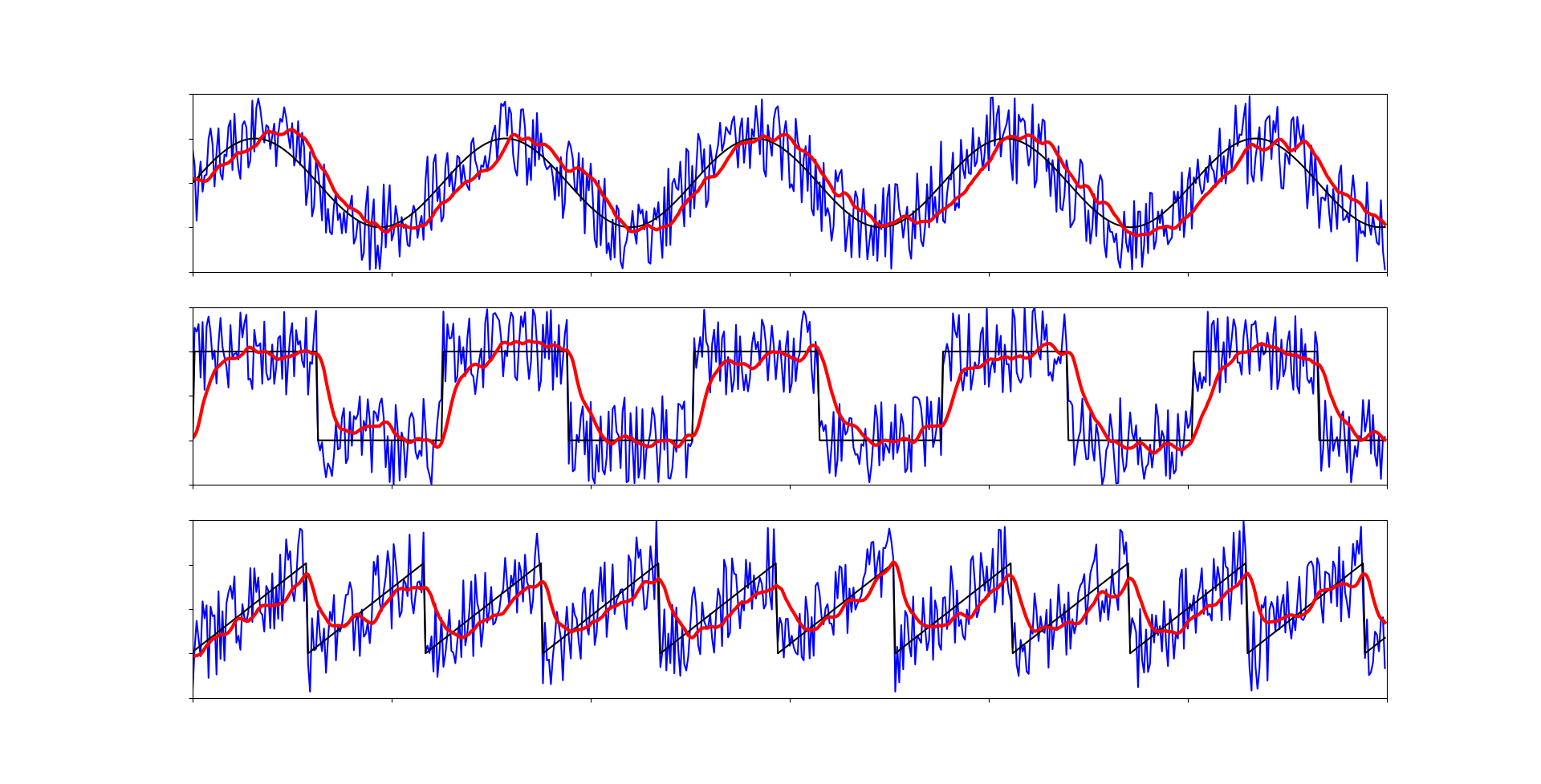
Примерами будут три графика - синусоида, квадратный сигнал (или дискретный, или цифровой) и треугольный сигнал (или пилообразный).
Код для вывода графиков
import matplotlib.pyplot as plt
from math import sin
# Generals variables
length = 30
resolution = 20
# Creating arrays with graphic
sinus_g = [sin(i / resolution) for i in range(length * resolution)]
square_g = [(1 if p > 0 else -1) for p in sinus_g]
triangle_g = []
t = -1
for _ in range(length * resolution):
t = t+0.035 if t < 1 else -1
triangle_g.append(t)
# Output of graphs
graphics = [sinus_g, square_g, triangle_g]
fig, axs = plt.subplots(3, 1)
for i in range(len(graphics)):
axs[i].plot(graphics[i])
axs[i].set_ylim([-2, 2]), axs[i].set_xlim([0, length*resolution]),
axs[i].set_yticklabels([]), axs[i].set_xticklabels([])
plt.show()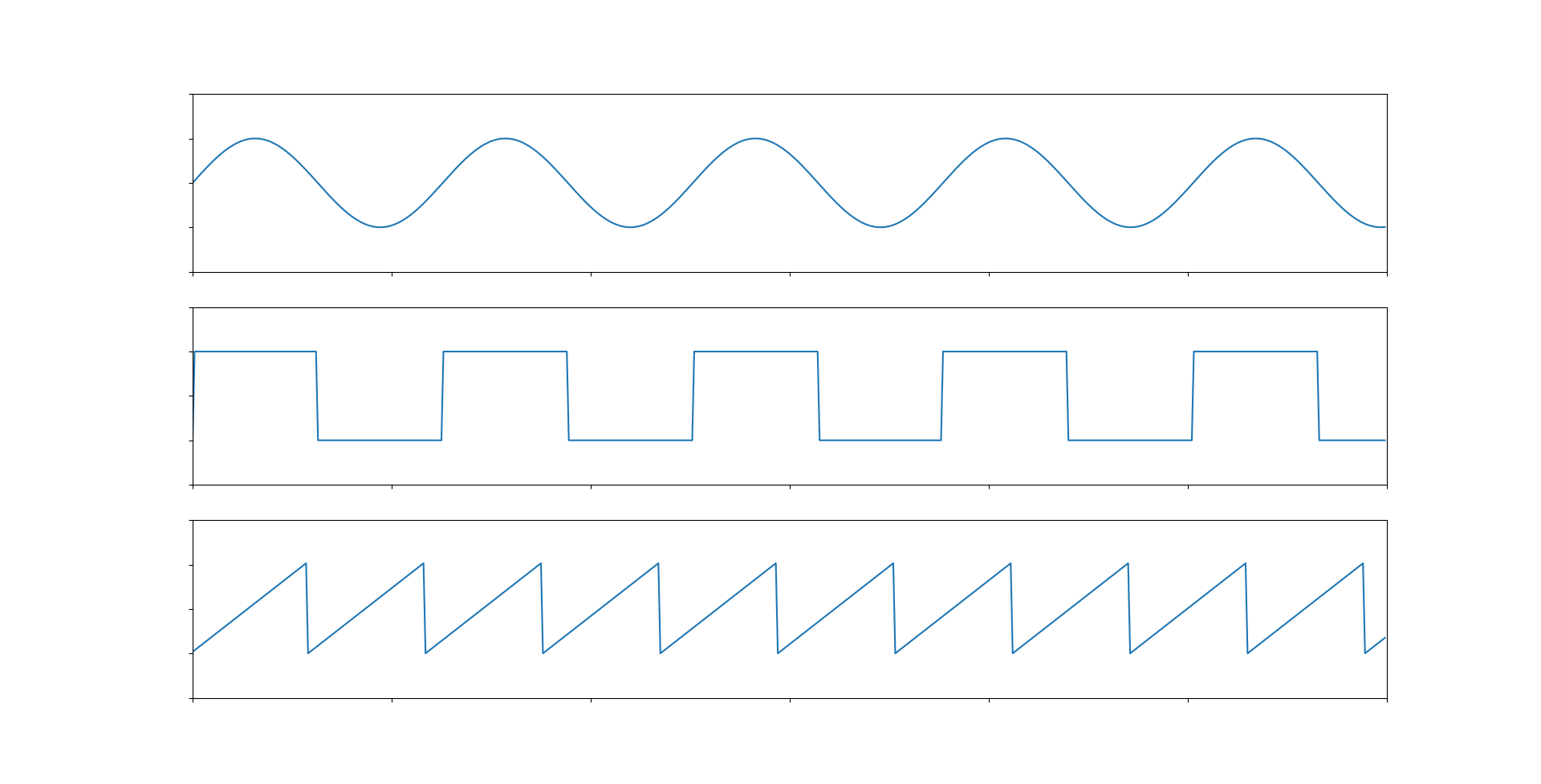
Бороться мы будем с двумя видами шума: постоянный шум (аддитивный белый гауссовский шум или АБГШ) с относительно стабильной амплитудой и случайные импульсы, вызванные внешними факторами. Амплитудой шума - стандартное отклонение зашумленного сигнала от не зашумленного.
Симулировать это мы будем данным образом.
Функция для добавление шума
def noised(func, k=0.3, prob=0.03):
o = []
for p in func:
r = (np.random.random()*2-1) * k
# Standard noise and random emissions
if np.random.random() < prob: c = p + r*7
else: c = p + r
o.append(c)
return o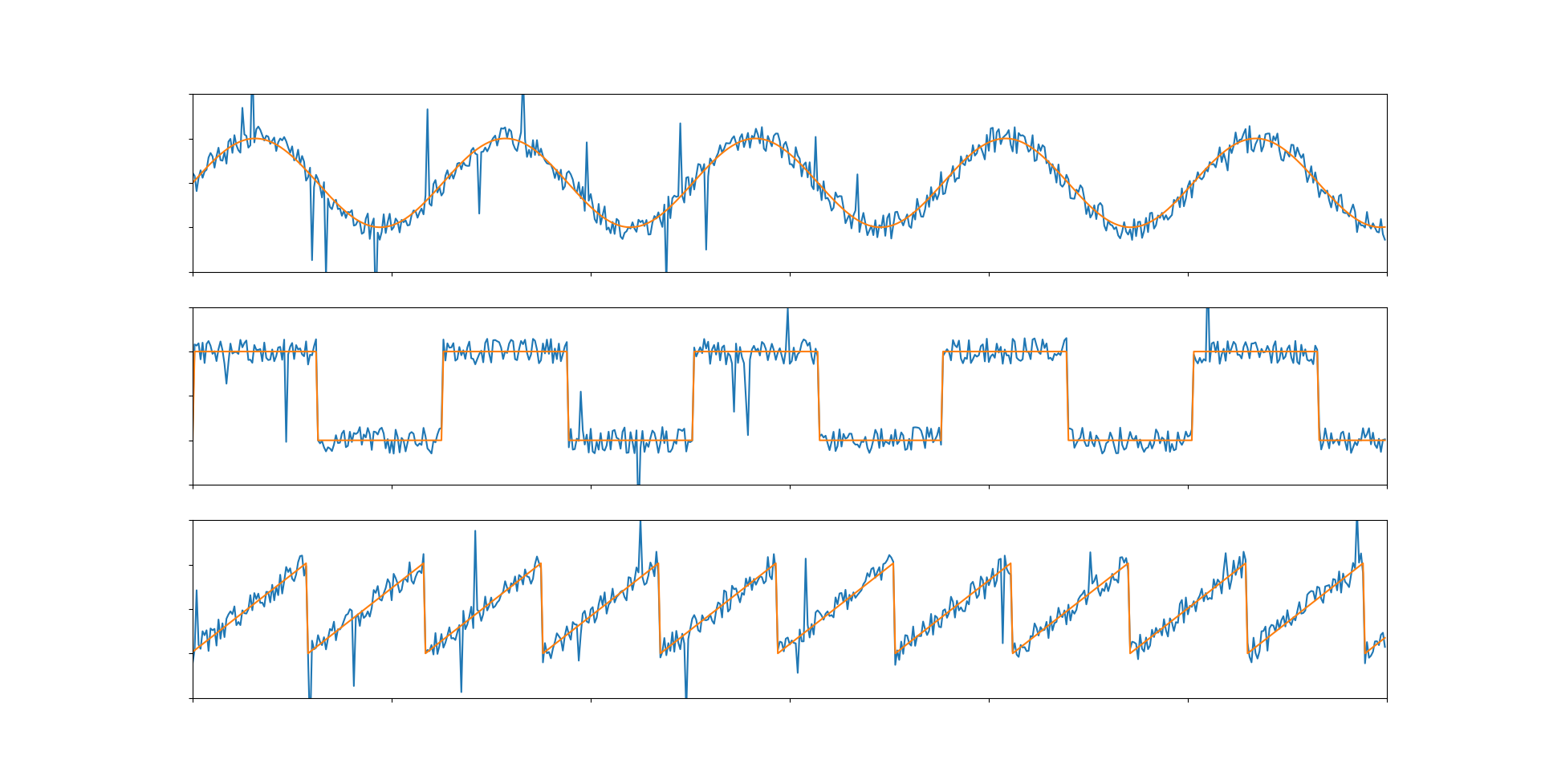
Среднее арифметическое
Как по мне, самый очевидный способ минимизировать шум. Для его реализации потребуется ввести буфер нескольких предыдущих значений, каждый раз, когда опрашивается датчик буфер сдвигается (первый элемент удаляется, а новое значение датчика добавляется в конец или как-нибудь по другому, главное фиксированный размер буфера). От его размера и будет зависеть результат и быстродействие кода. С фильтрацией алгоритм справляется очень неплохо. Но его проблема заключается в производительности. Контроллеру приходится делать множество вычислений с плавающей точкой, что может сказаться на скорости выполнения кода. Но если датчик не следует очень часто опрашивать, то этот метод отлично подойдет.
Код фильтрация графика средним арифметическим
def arith_mean(f, buffer_size=10):
# Creating buffer
if not hasattr(arith_mean, "buffer"):
arith_mean.buffer = [f] * buffer_size
# Move buffer to actually values ( [0, 1, 2, 3] -> [1, 2, 3, 4] )
arith_mean.buffer = arith_mean.buffer[1:]
arith_mean.buffer.append(f)
# Calculation arithmetic mean
mean = 0
for e in arith_mean.buffer: mean += e
mean /= len(arith_mean.buffer)
return mean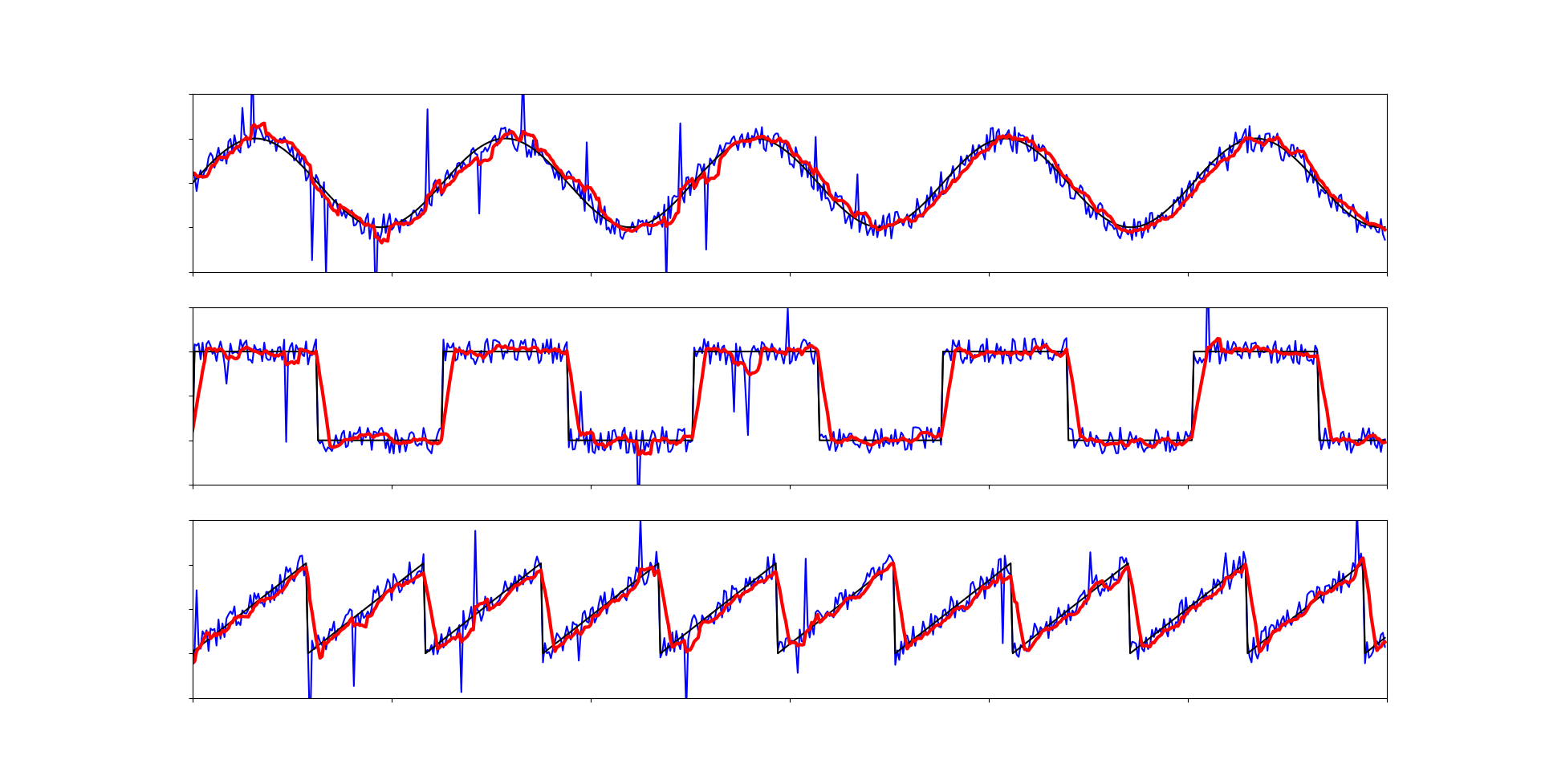
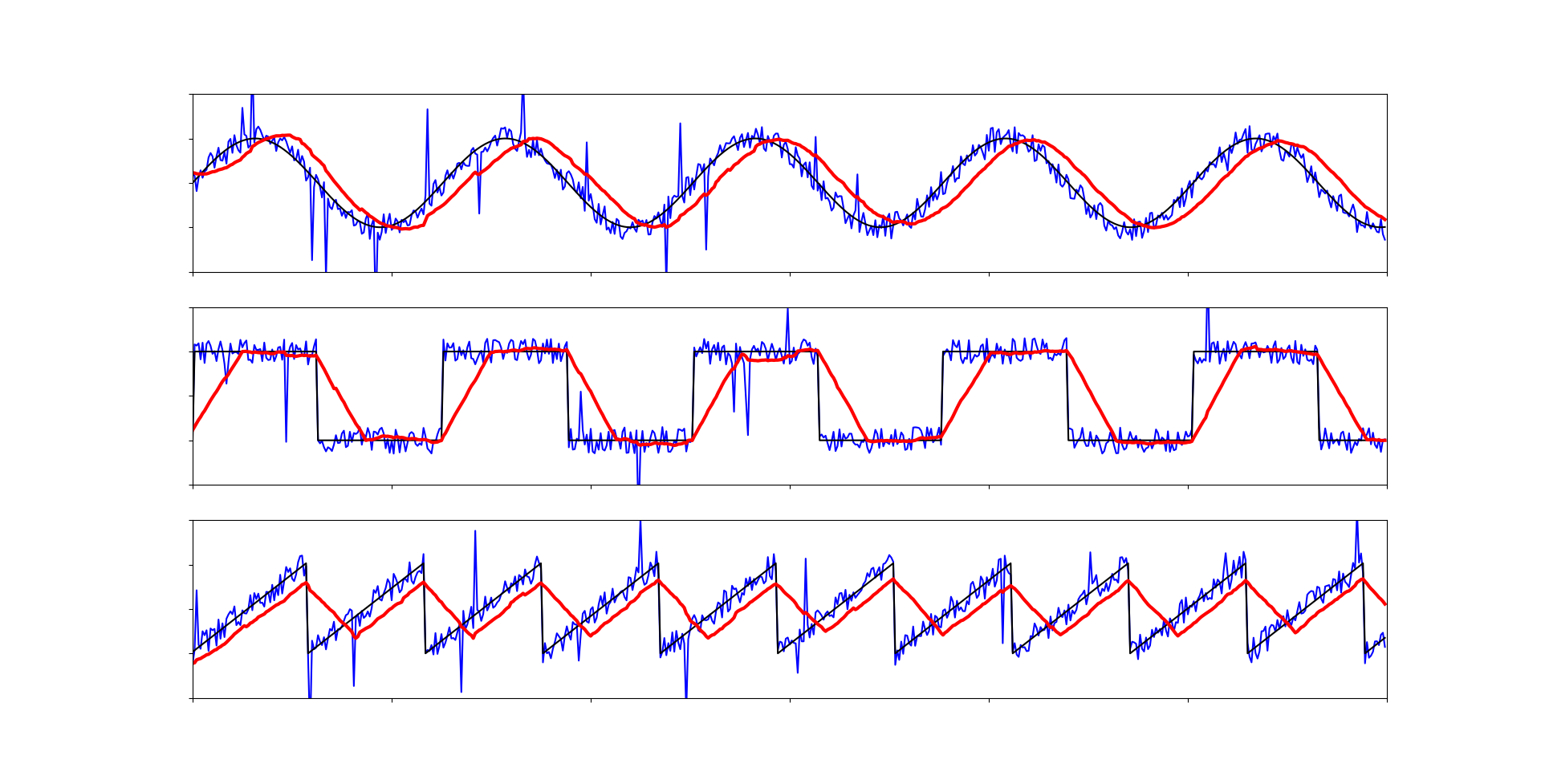
Как мы видим, при увеличении буфера квадратный и треугольный сигналы сильно исказились, а синусоида сместилась. Проявляется запаздывание среднего значения. Так что, при использовании данного фильтра стоит аккуратнее подбирать размер буфера.
Медианный фильтр
Медианный фильтр предназначен справляться со случайными импульсами. Если среднее арифметическое получая на вход (10, 12, 55), выдаст 25.67, то медиан выдаст 12. На первый взгляд не так просто понять как он устроен, но со своей задачей он справляется отлично. На просторах интернета я нашел лаконичное исполнение. Но оно подойдет только в случаях когда длительность импульса не более одного шага, иначе придется использовать другое исполнение медианы высшего порядка.
middle = (max(a,b) == max(b, c)) ? max(a, c) : max(b, min(a, c)); // c++middle = max(a, c) if (max(a, b) == max(b, c)) else max(b, min(a, c)) # pythonКод медианного фильтра
def median(f):
# Creating buffer
if not hasattr(median, "buffer"):
median.buffer = [f] * 3
# Move buffer to actually values ( [0, 1, 2] -> [1, 2, 3] )
median.buffer = median.buffer[1:]
median.buffer.append(f)
# Calculation median
a = median.buffer[0]
b = median.buffer[1]
c = median.buffer[2]
middle = max(a, c) if (max(a, b) == max(b, c)) else max(b, min(a, c))
return middle
Медианный фильтр справился почти со всеми импульсами. К тому же этот алгоритм совершенно прост в вычислении. И используя его в комбинации с каким-либо другим другим фильтром можно получить максимальный результат.
Экспоненциальное бегущее среднее и адаптивный коэффициент
Этот фильтр по своей сути схож с первым, а главное он более простой по вычислениям. Работает он так: к предыдущему фильтрованному значению прибавляется новое, и каждое из них помножено на собственный коэффициент, сумма которых равна 1. Коэффициент k подбирается от 0 до 1 и означает важность нового значения по сравнению с предыдущем, то есть чем больше k, тем больше важность нового нефильтрованного значения и фильтрованный график ближе к изначальному.
normalised = new * k + normalised * (1-k) # Эта формулаnormalised += (new - normalised) * k # А лучше этаАдаптивный коэффициент нужен для корректной фильтрации квадратных сигналов. Реализуется он в одну строчку и означает, что если предыдущее фильтрованное значение слишком далеко от нового (то есть корректный сигнал изменился), то k увеличиваем чтобы момент смены сигнала был четко виден, а иначе k оставляем нормальным.
k = s_k if (abs(new - normalised) < d) else max_kКод фильтра экспоненциального бегущего среднего с адаптивным коэффициент
def easy_mean(f, s_k=0.2, max_k=0.9, d=1.5):
# Creating static variable
if not hasattr(easy_mean, "fit"):
easy_mean.fit = f
# Adaptive ratio
k = s_k if (abs(f - easy_mean.fit) < d) else max_k
# Calculation easy mean
easy_mean.fit += (f - easy_mean.fit) * k
return easy_mean.fit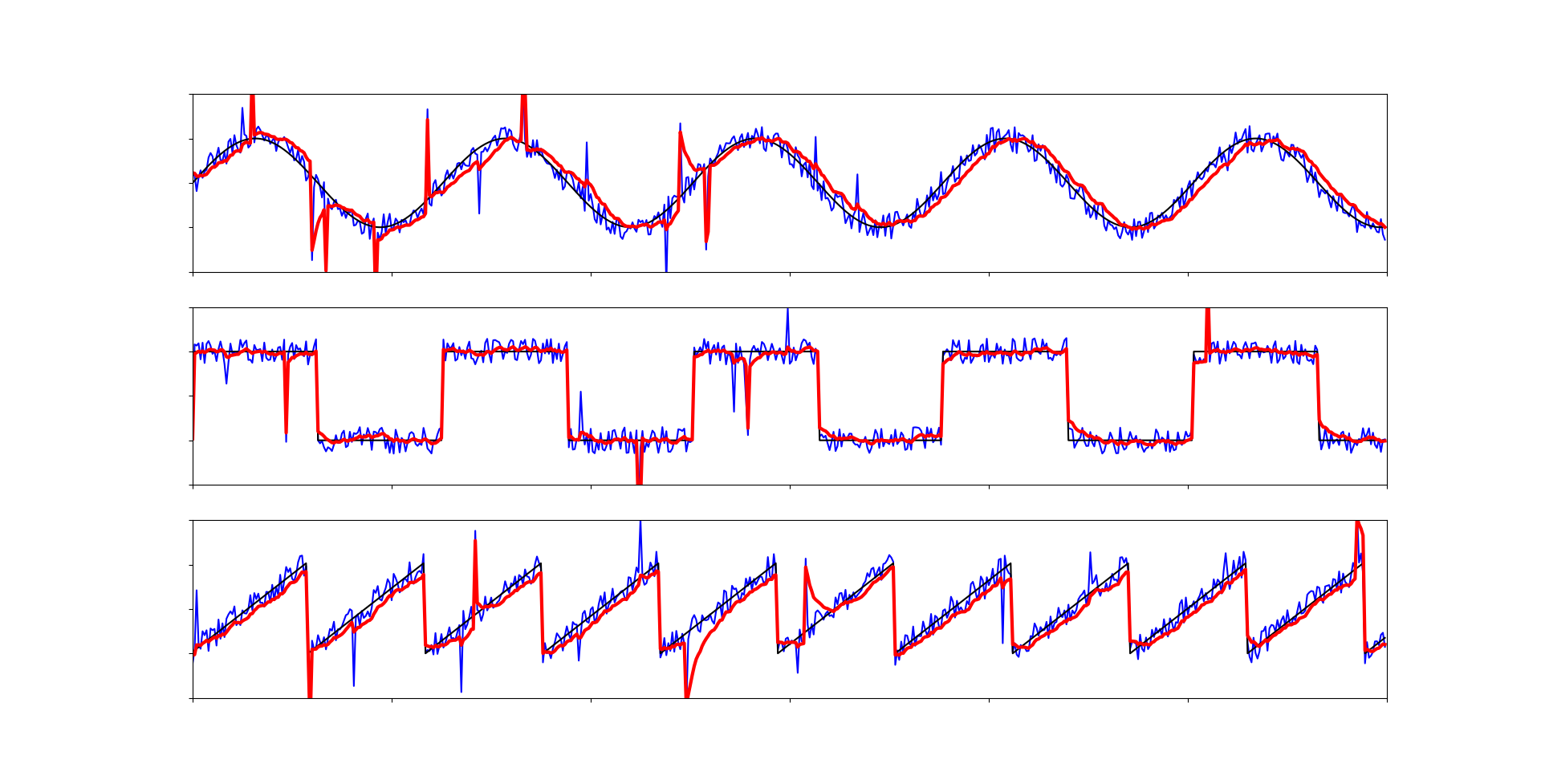
Работает достаточно хорошо, но из-за адаптивного коэффициента появляются некие артефакты в моментах с импульсами, так как они достаточно велики, чтобы определиться как составляющие квадратного сигнала. С этим можно бороться, увеличивая параметр d (требуемое расстояние для определения квадратного сигнала), но есть решение элегантнее. И тут нам как раз нам потребуется медианный фильтр. Если перед подачей данных на бегущее среднее, прогнать их через медиану, то можно получить качественный и быстродейственный алгоритм для фильтрации сигнала.
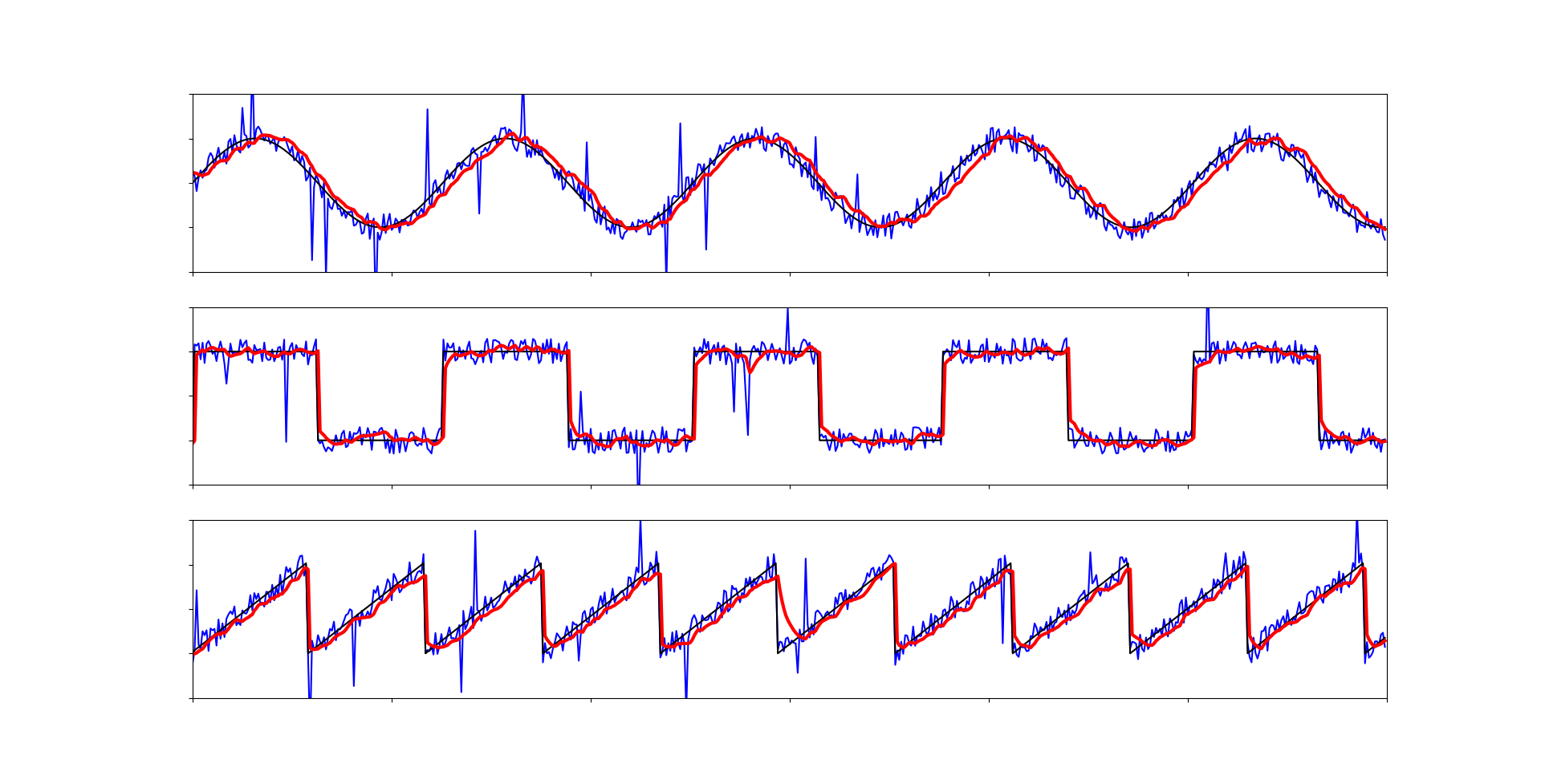
Все артефакты исчезли. Данная связка алгоритмов является одной из самых эффективных и быстродейственных. Она может быть применена практически везде.
Применение связки фильтров
def normalise(func):
o = []
for p in func:
res = median(p)
res = easy_mean(res)
o.append(res)
return oФильтр Калмана
Еще один фильтр, принцип работы которого не столь очевиден для каждого. Из всего кода необходимо знать, что r - это приблизительная амплитуда шума, а q - ковариационное значение процесса, и его следует подбирать самостоятельно. Если вы хотите разобраться в устройстве фильтра Калмана поподробнее, можете прочитать эту статью с википедии, а код я взял и отредактировал с этой страницы.
Код фильтра Калмана
def kalman(f, q=0.25, r=0.7):
if not hasattr(kalman, "Accumulated_Error"):
kalman.Accumulated_Error = 1
kalman.kalman_adc_old = 0
if abs(f-kalman.kalman_adc_old)/50 > 0.25:
Old_Input = f*0.382 + kalman.kalman_adc_old*0.618
else:
Old_Input = kalman.kalman_adc_old
Old_Error_All = (kalman.Accumulated_Error**2 + q**2)**0.5
H = Old_Error_All**2/(Old_Error_All**2 + r**2)
kalman_adc = Old_Input + H * (f - Old_Input)
kalman.Accumulated_Error = ((1 - H)*Old_Error_All**2)**0.5
kalman.kalman_adc_old = kalman_adc
return kalman_adc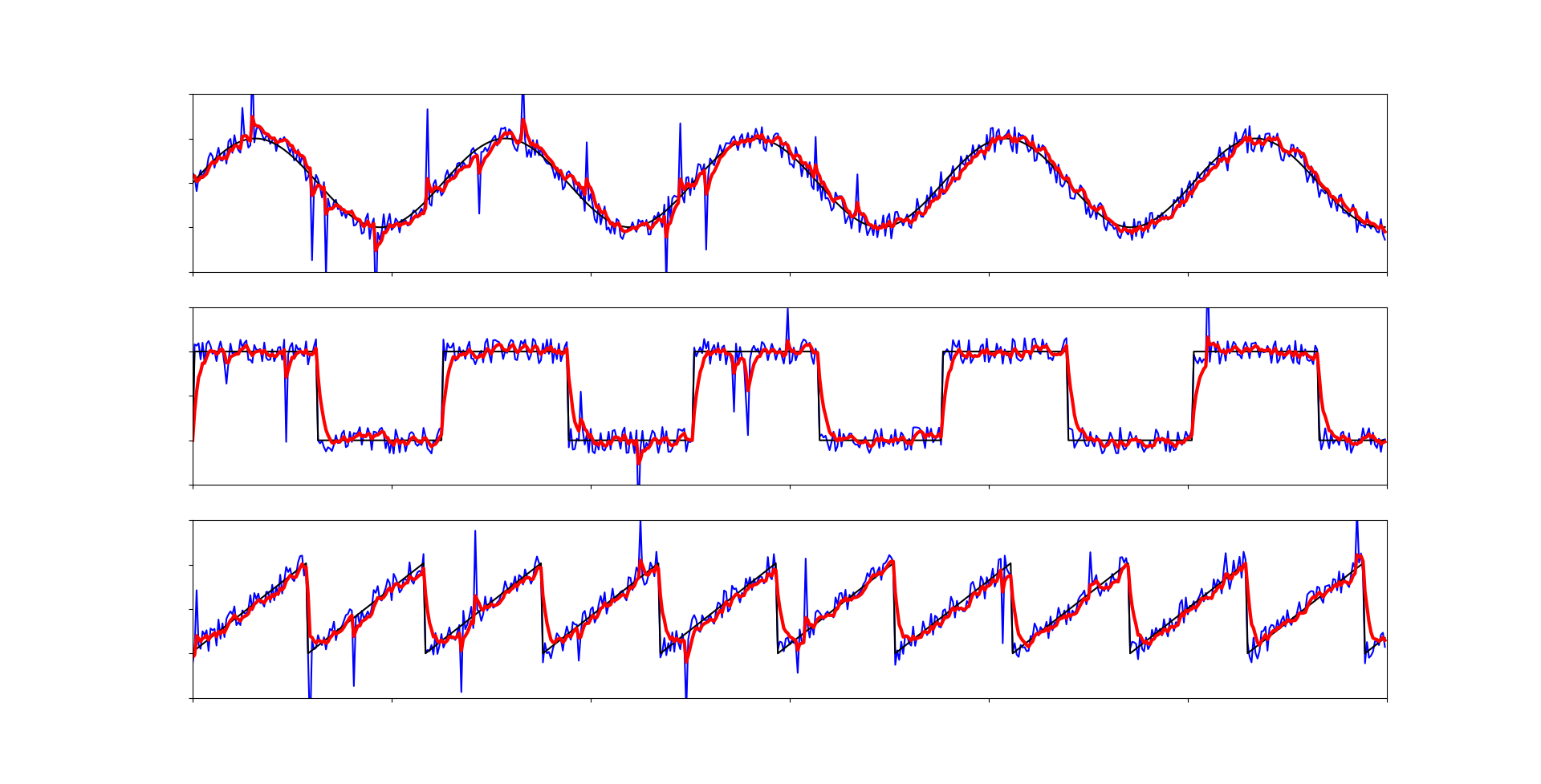
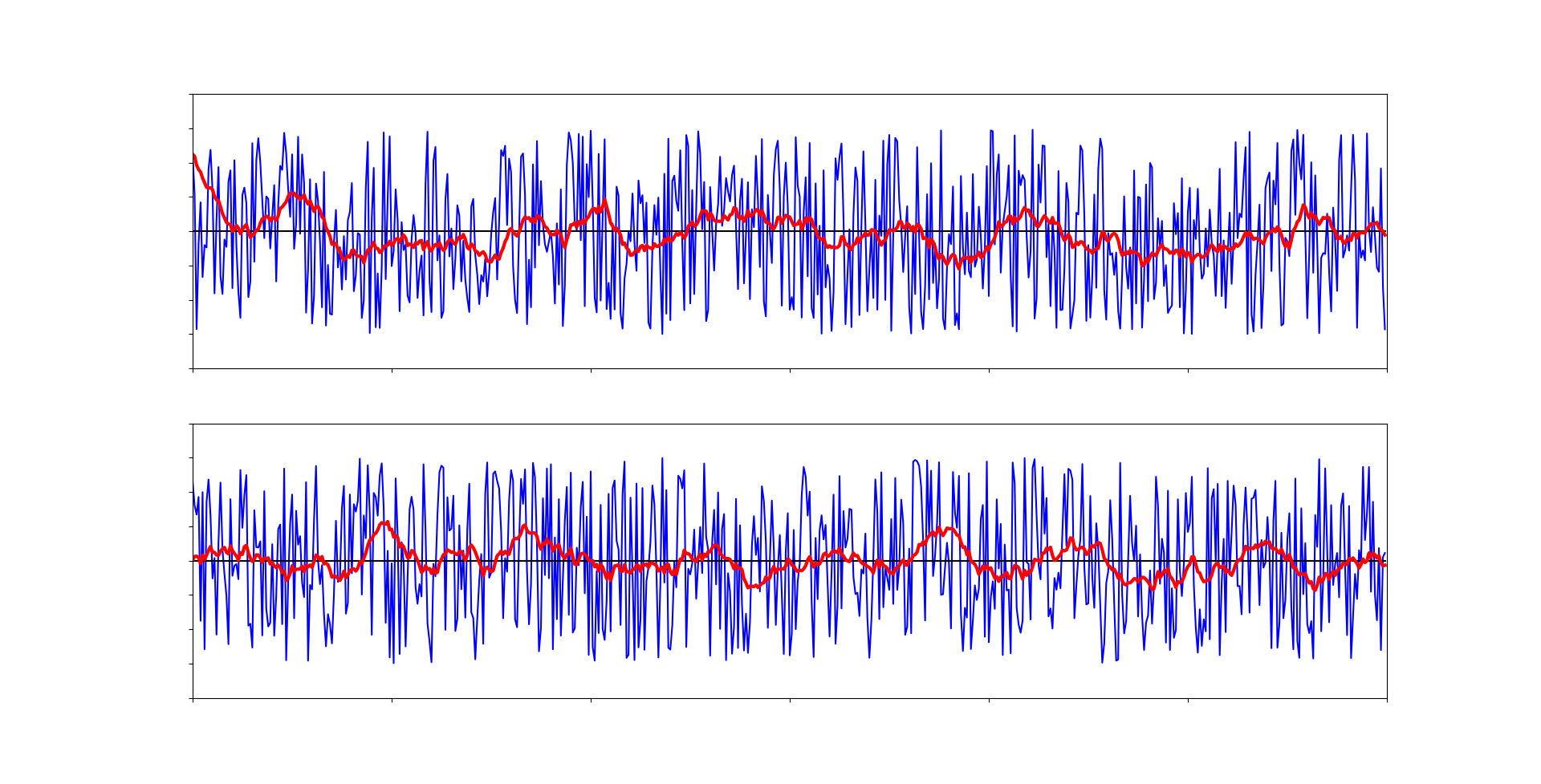
Со своей задачей фильтр справляется, но он не всегда подойдет из-за множества вычислений с плавающей точкой.
Какой фильтр выбрать?
Это зависит от обстоятельств в которых фильтр будет использоваться. Естественно стоит попробовать каждый, но практически для каждого случая подойдёт вариант №2 из списка ниже. Напомню, что наиболее выгодная связка - медианного фильтра с другим. Пройдемся вкратце по перечисленным фильтрам из данной статьи:
Медианный фильтр - самый быстродейственный алгоритм, применятся для отсеивания случайных импульсов, наиболее эффективен в связках с другими алгоритмами.
Экспоненциальное бегущее среднее с адаптивным коэффициент - универсальный, и простой фильтр, подойдет в большинстве ситуаций
Среднее арифметическое - эффективный, но не всегда столь быстродейственный алгоритм
Фильтр Калмана - универсальный способ фильтрации любого сигнала, но громоздкий по вычислениям
Кстати, если вы работаете со средой arduino, то там присутствует удобный инструмент визуализации графиков из значений переданных в порт, статья об этом. Это может упростить работу с сигналами.
В данной статье я не стал затрагивать большую часть терминологии ради доступности. И естественно, фильтры предоставленные в этой статье - это лишь малая часть от всех существующих, и если вы не нашли интересующую информацию по данной теме или предоставленные фильтры не дали достаточный результат, то я рекомендую поподробнее разобраться в теме цифровой фильтрации.
И на последок исходники кодов, и еще несколько примеров...
Код для визуализация графиков
import matplotlib.pyplot as plt
from math import sin
from _f import *
# Generals variables
length = 30
resolution = 20
# Creating arrays with graphic
sinus_g = [sin(i / resolution) for i in range(length * resolution)]
square_g = [(1 if p > 0 else -1) for p in sinus_g]
triangle_g = []
t = -1
for _ in range(length * resolution):
t = t+0.035 if t < 1 else -1
triangle_g.append(t)
# Output of graphs
graphics = [sinus_g, square_g, triangle_g]
fig, axs = plt.subplots(3, 1)
for i in range(len(graphics)):
noised_f = noised(graphics[i])
axs[i].plot(noised_f, color='blue')
axs[i].plot(graphics[i], color='black')
axs[i].plot(normalise(noised_f), linewidth=3, color='red')
axs[i].set_ylim([-2, 2]), axs[i].set_xlim([0, length*resolution]),
axs[i].set_yticklabels([]), axs[i].set_xticklabels([])
plt.show()
Код с фильтрами
import numpy as np
np.random.seed(58008)
def normalise(func):
o = []
for p in func:
res = median(p)
res = easy_mean(res)
o.append(res)
return o
def noised(func, k=0.3, fitob=0.03):
o = []
for p in func:
r = (np.random.random()*2-1) * k
# Standard noise and random emissions
if np.random.random() < fitob: c = p + r*7
else: c = p + r
o.append(c)
return o
def arith_mean(f, buffer_size=10):
# Creating buffer
if not hasattr(arith_mean, "buffer"):
arith_mean.buffer = [f] * buffer_size
# Move buffer to actually values ( [0, 1, 2, 3] -> [1, 2, 3, 4] )
arith_mean.buffer = arith_mean.buffer[1:]
arith_mean.buffer.append(f)
# Calculation arithmetic mean
mean = 0
for e in arith_mean.buffer: mean += e
mean /= len(arith_mean.buffer)
return mean
def easy_mean(f, s_k=0.2, max_k=0.9, d=1.5):
# Creating static variable
if not hasattr(easy_mean, "fit"):
easy_mean.fit = f
# Adaptive ratio
k = s_k if (abs(f - easy_mean.fit) < d) else max_k
# Calculation easy mean
easy_mean.fit += (f - easy_mean.fit) * k
return easy_mean.fit
def median(f):
# Creating buffer
if not hasattr(median, "buffer"):
median.buffer = [f] * 3
# Move buffer to actually values ( [0, 1, 2] -> [1, 2, 3] )
median.buffer = median.buffer[1:]
median.buffer.append(f)
# Calculation median
a = median.buffer[0]
b = median.buffer[1]
c = median.buffer[2]
middle = max(a, c) if (max(a, b) == max(b, c)) else max(b, min(a, c))
return middle
def kalman(f, q=0.25, r=0.7):
if not hasattr(kalman, "Accumulated_Error"):
kalman.Accumulated_Error = 1
kalman.kalman_adc_old = 0
if abs(f-kalman.kalman_adc_old)/50 > 0.25:
Old_Input = f*0.382 + kalman.kalman_adc_old*0.618
else:
Old_Input = kalman.kalman_adc_old
Old_Error_All = (kalman.Accumulated_Error**2 + q**2)**(1/2)
H = Old_Error_All**2/(Old_Error_All**2 + r**2)
kalman_adc = Old_Input + H * (f - Old_Input)
kalman.Accumulated_Error = ((1 - H)*Old_Error_All**2)**(1/2)
kalman.kalman_adc_old = kalman_adc
return kalman_adc
Ещё интересный эксперимент: я построчно загрузил зашумленную картинку своего кота и пропустил её через фильтр Калмана.

Комментарии (38)

Nagdiel
10.11.2021 12:39+13Такую статью было бы неплохо начать с того, чтобы определить какие бывают виды шума (аддитивный, мультипликативный, импульсный и т.д.) и с какими из них Вы собираетесь бороться. Выбор способа фильтрации зависит как от характера фильтруемого сигнала, так и от характера действующего в канале шума.
Медианный фильтр предназначен для борьбы с импульсным шумом. Похоже, что Ваша реализация медианного фильтра станет бесполезной, если ширина импульсов будет больше одной единицы дискретизации.Фильтр Калмана
Еще один фильтр, принцип работы которого не столь очевиден для каждого. Из всего кода вам необходимо знать, что r — это приблизительная амплитуда шума, а q следует подбирать самостоятельно.
Хотелось бы понять, что такое амплитуда шума (или шире — амплитуда случайного процесса), к тому же еще и приблизительная? И по каким принципам следует подбирать q?
Усредняющий фильтр может быть реализован по рекурсивной схеме, поэтому выводы о большой вычислительной сложности такого способа фильтрации не выглядят обоснованными.
iShrimp
10.11.2021 18:06Против редких импульсных помех существуют медианные фильтры различной ширины, взвешенные медианы, LULU и др., но важно знать, какую долю отсчётов могут составлять помехи. В случае, когда помехи частые и высокочастотные, я использовал гибрид медианного фильтра и среднего арифметического - берём 5 последовательных значений, сортируем по возрастанию, отбрасываем крайние, а остальные усредняем. Реализация очень простая:
из 5 значений находим максимальное и минимальное;
вычитаем их из общей суммы и результат делим на 3.
Интересно, у этого фильтра есть название? Не могу нагуглить ничего похожего.

Nagdiel
10.11.2021 20:45Тут, пожалуй, полезно упомянуть еще о таких обстоятельствах.
1) Медианный фильтр не даст эффект, если ширина импульса помехи превышает половину ширины окна фильтра.
2) Ранговые фильтры обычно требуют большого числа операций сравнения (для сортировки последовательности или поиска ранговых статистик), а в случае двумерной фильтрации дополнительно накладывается тот факт, что такие фильтры не являются сепарабельными. Поэтому утверждать, что медианный фильтр по вычислительным затратам лучше, чем другие сопоставимые по размеру окна фильтры я бы, пожалуй, не стал. Особенно, если речь идет о применении алгоритма фильтрации на сигнальном процессоре, адаптированном скорее на такие операции, как умножение с накоплением.Интересно, у этого фильтра есть название? Не могу нагуглить ничего похожего.
Вот именно такой вариант мне лично не попадался. Если я правильно понял, получается тот же усредняющий фильтр, но с коррекцией на возможность появления выбросов. Подобные эвристики, надо сказать, встречаются часто. Можно было бы, например, отбрасывать значения не по принципу минимума и максимума в окне, а сравнивать с фиксированным или адаптивным порогом (опять же как пример, выбрасывать из статистики значения у которых отклонения от матожидания превышают K оценочных значений СКО и т.п.). Можно просто усреднять с весами, обратно зависящими от прогнозируемого значения СКО (дисперсии). Или еще один пример. Если используется фильтра Калмана, можно анализировать отклонение в текущей точке от прогноза, и, если оно большое, не делать обновление, а использовать прогнозируемое значение на данном шаге. В принципе, при резких отклонениях какое-то время экстраполяция на основе прогноза может быть достаточно удовлетворительной, и при этом не требуется ранжировать элементы в каждом положении окна фильтрации.

adeshere
11.11.2021 02:09+2Я вот тоже подумал, что белый шум на практике встречается очень редко (во всяком случае у нас в геофизике). Гораздо чаще приходится иметь дело с фликкер-шумом, а импульсные помехи обычно следуют пачками, во всяком случае при геофизическом мониторинге. Особенно если они техногенные... Поэтому статье плюс, но при развитии темы было бы интересно увидеть чуть более развернутые и реалистичные модели шумов.
Ну и понятно, что размер буфера должен быть параметром метода, а никак не константой. Вообще, при фильтрации реальных сигналов больше всего времени обычно уходит на выбор оптимальных размеров окон для каждого фильтра. Я понимаю, что это переусложнит статью (и тогда она может потерять в наглядности). Но теперь "Введение в тему" уже есть, поэтому в следующей статье (если продолжение будет) можно было бы копнуть чуть поглубже...
А еще можно было бы добавить в статью абзац про причинные и симметричные фильтры. Если сигнал обрабатывается не в реальном времени, а ретроспективно (это довольно широкий класс научных задач), то симметричное окно обычно дает более качественные результаты.
Кстати, кроме прямоугольного и экспоненциального окна, рассмотренных в статье, существует огромное множество других сглаживающих ядер. Лично мне больше нравится гауссиан - он довольно эффективно эмулирует частотную фильтрацию для сигналов с пропусками (а у нас они есть всегда). Дело в том, что обычные частотные фильтры имеют знакопеременные фильтрующие (сверточные) последовательности, и при наличии пропусков это часто приводит к проблемам. Если же пересчитывать фильтр для каждого нового набора пропущенных наблюдений в окне, то это ужасно долго. (Заранее рассчитать все варианты фильтра можно только для очень маленьких окон - число комбинаций растет, как 2^N).
В такой ситуации гауссиан представляется неплохим компромиссным решением: при вычислении свертки одновременно считается сумма Sw весовых коэффициентов фильтра, и затем результат умножается на 1/Sw, что эквивалентно перенормировке последовательности. Получается быстро и дешево... ну а неизбежное искажение АЧХ на участках с сигнала с пропусками обычно не очень критично.

sci_nov
10.11.2021 13:11+2Достоинство этой публикации - простота, позволяющая неплохо познать основы, так сказать "затравка" для начинающих. А терминологию можно позже изучить, по советским книжкам.

akhkmed
10.11.2021 14:31Спасибо за ваш комментарий, благодаря нему прочитал вашу статью про сглаживание. Подскажите, смотреть на АЧХ фильтра есть смысл ведь только если известна АЧХ шума? Но как правильно усреднять(уточнять) результаты измерения, если измеряемая величина постоянна, а измерений произведено несколько в случайные моменты времени?

sci_nov
10.11.2021 15:23Видимо да, т.е. если известна СПМ шума. Последний вопрос не понял: если величина константа, то зачем ее несколько раз измерять?

Nagdiel
10.11.2021 15:36Вероятно здесь имеют в виду, что измерения сопровождаются шумом. Например, камера смотрит на стационарный фон но измерения яркости каждого пикселя зашумлены из-за теплового дрейфа и ошибок дискретизации. В этом случае яркость отдельного пикселя во времени есть константа, но наблюдаемая в виде аддитивной смеси с шумовыми отсчетами.
Ну или просто величина медленно меняется так, что на каком-либо отдельном интервале наблюдения ее значение можно принять в качестве константы.
sci_nov
10.11.2021 15:45Тогда именно СПМ шума важна, когда мы измеряем в пространственной точке. Это фильтр Винера.

sci_nov
10.11.2021 15:47Квадрат АЧХ фильтра, G(f), должен стремиться к обратной СПМ шума: G(f) ~ 1 / N(f)

sci_nov
10.11.2021 15:53и, скорее всего, калмановский фильтр сойдется к винеровскому при правильной его настройке, т.е. при учете именно СПМ шума (т.е. динамической модели системы, генерирующей шум).

Nagdiel
10.11.2021 16:35+1Если, я правильно помню теорию, то для такой сходимости достаточно чтобы сигнал и шум были стационарными процессами. Фильтр Винера как раз для такой модели и строится.
Фильтр Калмана, в свою очередь, допускает нестационарность процессов.

sci_nov
10.11.2021 15:33Еще зависит от цели: отфильтровать шум, при этом не исказив сильно сигнал, т.е. зависит от баланса между степенью фильтрации шума и степенью искажения сигнала. По факту, АЧХ фильтра всё равно важна, равно как и ФЧХ.

FGV
10.11.2021 13:33+1Как то странно реализован фильтр "Калмана" у Вас и тот что по ссылке. Совсем не похож на тот что приведен в вики.

lexasss
10.11.2021 15:02Довольно очевидная оптимизация фильтра Калмана:
def kalman(f, q=0.25, r=0.7): if not hasattr(kalman, "Accumulated_Error"): kalman.Accumulated_Error_Sq = 1 kalman.kalman_adc_old = 0 if abs(f-kalman.kalman_adc_old) / 50 > 0.25: # здесь необходимо пояснение констант нот Old_Input = f*0.382 + kalman.kalman_adc_old*0.618 # возможно, здесь тоже else: Old_Input = kalman.kalman_adc_old Old_Error_Sq = kalman.Accumulated_Error_Sq + q**2 H = Old_Error_Sq / (Old_Error_Sq + r**2) kalman_adc = Old_Input + H * (f - Old_Input) kalman.Accumulated_Error_Sq = (1 - H) * Old_Error_Sq kalman.kalman_adc_old = kalman_adc return kalman_adcМожно ещё оптимизировать, вынеся квадраты q и r в переменные доступные извне и вызывая kalman(f) с одним параметром.
И тогда тяжёлых вычислений не останется

robomakerr
10.11.2021 15:51Было бы интересно послушать про более эффективные фильтры, типа Ходрика-Прескотта.
Или основанные на заранее известной динамической модели сигнала.
Nagdiel
10.11.2021 16:04+1Фильтр Ходрика-Прескотта, как я понял из его описания, предназначен для определенной цели — устранения циклической составляющей во временных рядах и выделения тренда. Эта задача отличается от классической постановки задачи фильтрации сигналов. Кроме того, говорить об эффективности и сравнивать эффективность чего-либо имеет смысл только применительно к конкретной задаче, а не абстрактно.
Или основанные на заранее известной динамической модели сигнала.
Фильтр Калмана основывается на модели сигнала (линейной) и модели шума измерений. Существуют обобщения для и нелинейных моделей, например — UKF. Кроме того, фильтр Калмана при определенных вводных, для которых он и выводится, является оптимальным с точки зрения минимума среднекваратичной ошибки, что отвечает на вопрос его эффективности/неэффективности в этих условиях.
robomakerr
11.11.2021 22:16Ну давайте считать циклическую составляющую шумом)
Эффективность — допустим, пускай это будет наилучшая фильтрация при минимальной задержке.
Если я правильно понял, фильтр Калмана использует только статистическую модель сигнала, без учета динамики (формы кривой)?
Вообще, откуда он берет модель сигнала? Сам считает постепенно, или ему её надо в готовом виде подать?
FGV
12.11.2021 04:39Вообще, откуда он берет модель сигнала? Сам считает постепенно, или ему её надо в готовом виде подать?
Модель системы задается матрицами F, B, Q. Дальше основываясь на этой модели фильтр на каждом шаге рассчитывает ковариационную матрицу P и прогноз текущего состояния объекта x.

robomakerr
12.11.2021 22:26Получается, модель в «состав фильтра» не входит, её пользователь сам должен как-то определить? Тогда термин «фильтр» сбивает с толку, это скорее алгоритм использования модели.
И тогда не совсем понятно, если у нас уже есть модель (например «сигнал — это синусоида»), зачем нам фильтр. Можно просто аппроксимировать входные зашумленные данные синусоидой, это и будет наилучший из возможных фильтров (наверное).
FGV
13.11.2021 16:25Получается, модель в «состав фильтра» не входит, её пользователь сам должен как-то определить?
Нет, модель системы входит в фильтр. Пользователь много чего должен определить для фильтра, например тот же вектор состояния объекта (набор координат с которым будет работать фильтр).
И тогда не совсем понятно, если у нас уже есть модель (например «сигнал — это синусоида»)
Модель не сигнала, модель системы! Короче говоря набор диф. уравнений связывающих элементы вектора состояния между собой. Используя данную модель производится оценка дисперсии вектора состояния.
Вобще для чистого наблюдения с течением времени ФК вырождается в ФНЧ 1-го порядка:
y = y + (x-y)*k,
где: y - выход ФК, x - вход, k = Q/(R+Q). Q,R - константы (параметры модели).

Nagdiel
12.11.2021 06:16Эффективность — допустим, пускай это будет наилучшая фильтрация при минимальной задержке.
Наилучшая по какому критерию? Для каких моделей?
Тот же Ходрик-Прескотт использует определенный критерий оптимальности, который, как я могу предположить, все таки введен эвристически из предположения о наличии тренда и циклических составляющих. Эффективность этого подхода в сравнении с другими можно оценить только экспериментально.
В фильтре Калмана задаются динамическая (линейная) модель сигнала и модель процесса наблюдения (измерения) в терминах пространства состояний. Стохастическая составляющая обусловлена наличием формирующего шума и шума измерений.
Борьба с циклическими составляющими и выделение тренда в каких-либо процессах — это, конечно, не та задача, для которой разрабатывался фильтр Калмана. Шумом обычно называют быстропротекающие случайные процессы, чаще всего отличимые по частотным составляющим от полезного сигнала. Как мне показалось, обсуждаемая статья написана именно в контексте борьбы именно с такими шумами.

Refridgerator
10.11.2021 15:58+4Среднее арифметическое можно выполнять за O(1), используя линию задержки — на каждой итерации прибавляя новое значение и вычитая старое, задержанное на необходимое количество отсчётов. Такая реализация хоть и не является устойчивой, но её устойчивость можно обеспечить либо в целочисленной арифметике, либо введя обратную связь с рекурсивным фильтром низких частот. Аналогичным образом можно реализовать и некоторые другие варианты среднего, со взвешенными коэффициентами.
Также в статье не рассмотрена фильтрация низких частот FIR и IIR фильтрами в целом, разновидностью которых и являются «бегущее среднее» и «экспоненциальное бегущее среднее», причём далеко не самыми оптимальными. В частности, для «бегущего среднего» существуют частоты, которые будут полностью подавлены из-за сложения в противофазе (когда период среднего арифметического кратен периоду синусоиды).
iShrimp
10.11.2021 17:02+1Конечно, для начала нужно правильно поставить задачу и оценить, хотя бы приблизительно, спектральные диапазоны полезного сигнала и шума (чем меньше они пересекаются, тем задача проще), их плотности распределения (медианный фильтр нужен в случае тяжёлых хвостов) и наличие корреляции.
Также надо знать, допустима ли задержка, или требуется отклик в реальном времени. Если задержка допустима, то лучше использовать симметричные фильтры, чем "скользящее среднее", которое вообще пора запретить в реальных приложениях :)

Refridgerator
11.11.2021 15:15+1Симметричные фильтры для задач подавления широкополосного шума мало подходят. Намного лучше подходит использовать в качестве ядра свёртки непосредственно оконные функции, как классические, так и новые. А ещё лучше использовать МНК с тригонометрическим базисом и перекрытием в 2 или 4 раза.
А про запрет скользящего среднего полностью поддерживаю.

adeshere
11.11.2021 01:36Мы у себя в программе уже очень давно именно так и делаем - считаем суммы для скользящего среднего инкрементально. Аналогично считаются всякие корреляции, регрессии и другие статистики скользящего окна (там же тоже идет накопление всяких сумм, которые затем каким-то способом комбинируются). Однако при вычислениях с плавающей точкой это приводит к накоплению ошибок округления. Поэтому пришлось добавить в настройки конфигурации специальный параметр - как часто программа пересчитывает среднее арифметическое заново. Когда длина рядов - десятки и сотни миллионов точек, а размер окна фильтрации - десятки и сотни тысяч, выбор между скоростью и точностью вычислений уже вполне становится компромиссным.
Но у нас специфические задачи: данные, как правило, обрабатываются не в реальном времени, а постфактум. Поэтому большие задержки, возникающие на некоторых точках, не слишком критичны.

belav
12.11.2021 11:51Суть статьи: есть такие фильтры, их можно иногда использовать, а ещё бывают помехи разные. можно попробовать каждый фильтр по отдельности или совместно... где результат будет похож на "правду", тот и используйте.

DmitrySukharev
12.11.2021 15:25+1Треугольный сигнал? Может всё же пилообразный?

pfg21
12.11.2021 18:25Пиловидный сигнал по сути подвид треугольного :)

Refridgerator
14.11.2021 14:47У треугольного сигнала гармоники затухают сильнее, а чётные гармоники отсутствуют вообще. Так что ни о каком подвиде не может быть и речи. К тому же названия сигналов по их форме — это стандарт.


stranger_shaman
Левая картинка смотрится лучше
Mihahanya Автор
Да, есть такое. Так получилось из-за того, что фильтр сгладил не только шум, но и более резкие переходы между цветами. К тому же я подавал на фильтр изображение строчками. Поэтому картинка выглядит более размытой по горизонтали.
Но в общем то так изображения никто и не фильтрует, я это сделал, потому-что было интересно, что из этого выйдет.
omxela
Вот ту хорошо бы сказать, имхо, что у медианного фильтра есть одно достоинство, которое часто необходимо: он сохраняет резкие перепады. Так что на зверьке можно попробовать двумерный медианный фильтр (в любом нормальном редакторе изображений он есть).