В работе построена объектная имитационная модель пула потоков, за основу которой взята реализация, используемая в СУБД MySQL, MariaDB и Percona Server. Описаны входные потоки модели и примеры их распределений. Приведены результаты апробации модели, согласующиеся с известными паттернами зависимости производительности от входных параметров. Практическое значение модель имеет как инструмент статического и динамического выявления наиболее значимых для производительности параметров и их оптимального выбора.
Введение
Имитационное моделирование используется для эффективного принятия решений не только в прикладных предметных областях, таких как различные отрасли народного хозяйства и военное дело, но также и в проектах, связанных с разработкой программного обеспечения и проектированием сложных IT-систем. Одной из таких систем является пул потоков (трэдпул), активно применяемых в самых разнообразных программных продуктах на протяжении последних примерно 25 лет. Данная технология появилась как альтернатива концепции «одно соединение – один поток», т.к. позволяет во многих случаях не только экономить ресурсы, но и повысить производительность программного продукта в целом. Она заключается в переиспользовании уже существующего потока для обработки следующей задачи.
Существует множество различных реализаций трэдпула, наиболее подробный обзор которых приведен в [9]. По отдельным реализациям имеется большое количество материалов. Так, один из первых трэдпулов для брокера объектных запросов CORBA описан в [13], трэдпул для Android — в [1], для сервера приложений Oracle GlassFish – в [10]. Поучительным примером эффективного использования модели трэдпула в Python для решения сложной научной задачи является [23]. Трэдпул от компании Microsoft для CLR описан в фундаментальном труде [16], а последняя реализация доступна в [20]. Собственное расширение модели потоков Java в виде трэдпула разработано в отечественном академическом исследовании [21]. Большое внимание уделяют этому вопросу также разработчики известных СУБД, в частности, MySQL [14], MariaDB[18], Percona Server[12]. Особенностями подхода, использованного в этих реализациях, является разделение всего трэдпула на группы потоков, где каждая группа имеет свои упорядоченные по приоритетам очереди запросов на обслуживание и свои подгруппы активных, ожидающих и свободных потоков; отдельный поток-таймер в таком трэдпуле отслеживает застрявшие потоки и запросы. Забегая вперед, отметим, что модель именно такой разновидности трэдпула рассматривается в данной работе.
Все трэдпулы характеризуются большим количеством параметров, которые назначаются
проектировщиком и оказывают влияние на итоговую эффективность трэдпула. Основным
из них является размер трэдпула, который задает ширину параллелизма (concurrency level), в качестве которой, например, для упомянутых выше СУБД-реализаций является количество групп. Этот выбор определяется множеством факторов, такими как общая нагрузка на сервер и профиль этой нагрузки (workload). Так, для CPU-ориентированной (CPU-bound) нагрузки и нагрузки, ориентированной на ввод-вывод (IO-bound), даже при одном и том же количестве
одновременных соединений оптимальные значения размера трэдпула могут коренным образом различаться. Именно поэтому большое число работ содержит в том или ином виде рекомендации, как же выбирать этот параметр. Назначать его следует, подстраивая под меняющуюся нагрузку. Делать это можно как из общих соображений, не отслеживая изменение произвоидельности и не пытаясь ее оптимизировать, так и с учетом ее изменения.
Первый подход рассмотрен в работах [1][7][8][10][11], где приведены различные вариации формул, опирающихся на доступное число процессоров, среднее время обслуживания запроса на CPU и среднее время простоя CPU из-за ввода-вывода, а также на известный в теории очередей закон Литтла. Что же касается алгоритмов с оптимизацией производительности, то здесь наибольших результатов добилась Microsoft. В получивших широкую известность работах [5][6] рассмотрено применение известного в теории метода HillClimbing для оптимизации размера трэдпула, практические же результаты этого применения описаны в [19]. В [4] описана, а в [20] реализована вариация HillClimbing-подхода, основанная не на вычислении градиента, а на преобразованиях Фурье, как обладающая большей устойчивостью к случайным воздействиям. Другие теоретические подходы к решению задачи динамического выбора размера трэдпула предложены в [9] и [17]. Кроме того, [17], опубликованная в 2021 году, содержит полную и актуальную библиографию вопроса.
Вместе с тем, дать более полное и глубокое представление о том, как же работает такая сложная система как трэдпул, может помочь имитационная модель. Итоговая производительность (выраженная, например, в среднем числе обслуженных запросов в единицу времени) зависит не только от размера трэдпула, но и от других параметров. Чтобы установить значимость их влияния требуется большое количество длительных и дорогих натурных экспериментов на рабочих серверах, а хорошо спроектированная имитационная модель позволит сделать это гораздо быстрее, собственно, это и есть ее основное достоинство для любых задач. Этот подход к исследованию трэдпула на данный момент апробирован еще довольно слабо. Можно отметить работу [2] (где использован специфический и малодоступный инструментарий) и недавнюю работу украинских специалистов [15], где применены стохастические сети Петри. Подход к моделированию и оптимизации трэдпула с помощью сетей Петри используется также в [22]. В данной работе предлагается имитационная модель трэдпула, где за основу моделируемой системы взята реализация, описанная в [12]. Сама модель реализована на языке C++ с помощью схемы, описанной в [24], позволяющей гибко учесть все алгоритмические нюансы системы в полном объеме. В разделе II описан сам трэдпул, в разделе III – архитектура предложенной модели, в разделе IV – некоторые результаты ее валидации, в разделе V – выводы и рекомендации по ее применению.
Описание моделируемого трэдпула
Если опустить вторичные детали, граф вызовов функций трэдпула выглядит так (рис. 1):
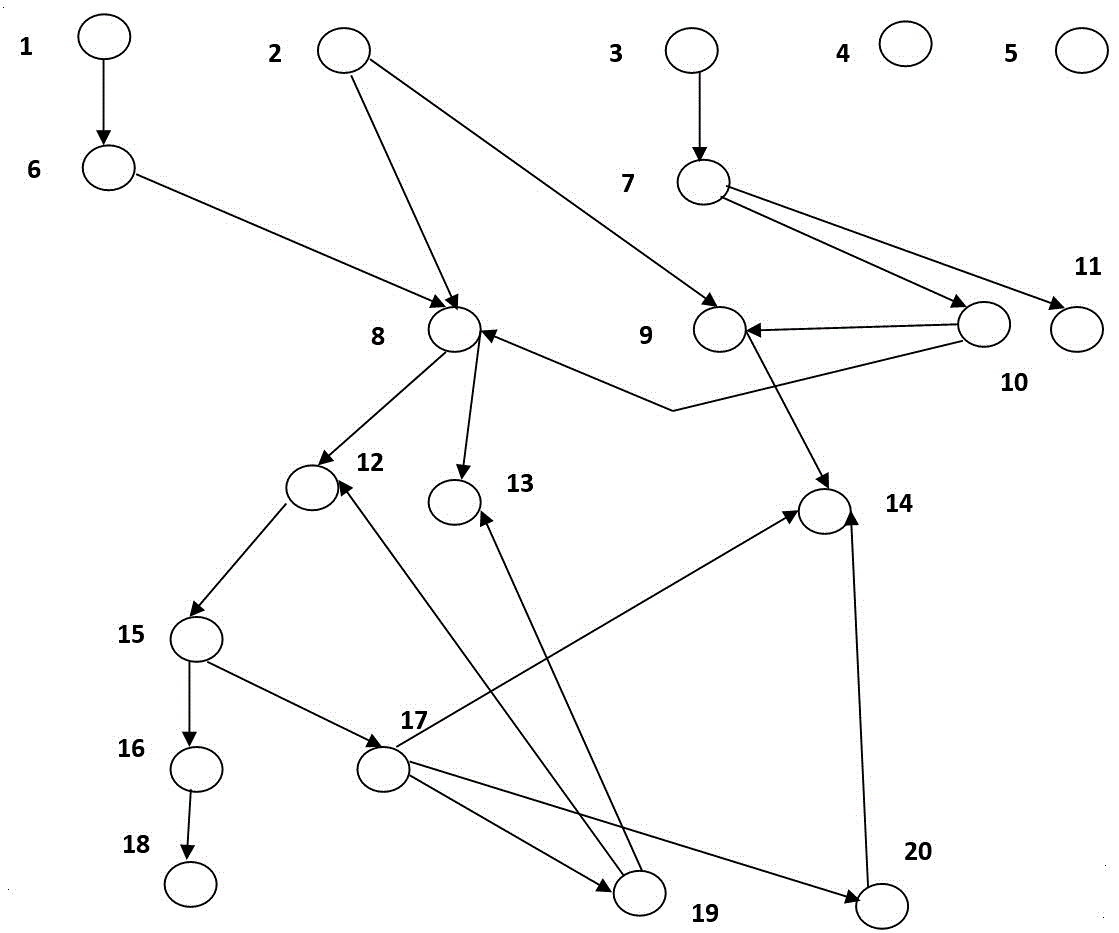
Рис. 1. Граф вызовов функций трэдпула, где обозначения соответствуют следующим функциям (Таблица 1):
Таблица 1. Описание функций трэдпула.
| Имя функции | Описание функции | Имя функции | Описание функции |
|---|---|---|---|
1 add_connection
|
Добавляет новое соединение, выбирает для него группу потоков | 11 timeout_check
|
Проверяет, не истек ли таймаут для обработки запроса; удаляет соединение, если истек |
2 wait_begin
|
Коллбэк для начала простоя потока из-за I/O | 12 create_worker
|
Создает новый поток |
3 start_timer
|
Запуск потока-таймера для отслеживания застрявших потоков | 13 wake_thread |
Будит неактивный поток |
4 set_tp_size
|
Задает размер трэдпула | 14 too_many_threads
|
Проверяет, не слишком ли много в группе активных потоков |
5 wait_end
|
Коллбэк для окончания простоя потока | 15 worker_main
|
Основная функция для потока из трэдпула |
6 queue_put
|
Запись нового соединения в очередь | 16 handle_event
|
Подготовка к выполнению запроса |
7 timer_thread
|
Основная функция для потока-таймера | 17 get_event
|
Назначает соединение готовому к работе потоку (дает ему работу) |
8 wakeCreateThread
|
Создает новый поток или будит неактивный | 18 process_request
|
Выполнение запроса потоком |
9 queues_are_empty
|
Проверяет, пусты ли очереди | 19 listener
|
Поток-поллинг, повторная выборка соединений на дескрипторе группы |
10 check_stall
|
Обрабатывает застрявшие потоки | 20 queue_get
|
Выборка соединения из очереди |
Описание имитационной модели
Перечислим случайные величины, являющиеся входными для модели и генерируемые датчиком случайных чисел в соответствии с выбранным распределением:
-
Входной поток соединений – распределение интервалов времени между вызовами функции
add_connection.
-
Длительность создания нового потока — тайминг для функции
create_worker.
-
Длительность одного раунда активности потока: от начала обработки запроса до первого вызова
wait_begin, либо между вызовамиwait_endиwait_begin, либо междуwait_endи завершением обработки запроса.
-
Длительность одного раунда простоя CPU: между вызовами
wait_beginиwait_end.
-
Количество активных раундов за время обслуживания одного запроса.
-
Время между завершением обслуживания запроса и выбором того же персистентного соединения процедурой поллинга для назначения ему нового потока и обслуживания следующего запроса.
Выходные значения модели – среднее число обслуженных запросов в секунду (queries per second) и средняя длительность обслуживания запроса (latency).
Модель реализована на следующих предметных классах: Threadpool (синглетон), Threadgroup, Connection, Thread, Timer(синглетон). Для экземпляров класса Thread установлены состояния:
-
creating – создание потока;
-
active – обслуживание запроса;
-
waiting – ожидание ввода-вывода;
-
idle – простой потока, когда запрос обслужен, а новый еще не назначен;
-
polling – в этом состоянии может находиться только поток, занятый поллингом (listener).
Для экземпляров класса Connection установлены состояния:
-
in usual queue – соединение ожидает назначения потока в обычной очереди;
-
in prio queue – соединение ожидает назначения потока в льготной очереди;
-
threading – соединению назначен поток, запрос обслуживается;
-
between – запрос обслужен, соединение ожидает выборки потоком-listener’ом.
Возможные переходы между состояниями показаны на рис. 2 и 3.
 |
 |
| Рис.2. Модель состояний для класса Thread | Рис. 3. Модель состояний для класса Connection |
Параметрами, которыми исследователь может варьировать для их оптимизации, помимо размера трэдпула (количества групп), являются следующие свойства класса Threadgroup:
-
oversubscribe – максимальное количество активных потоков в группе (по умолчанию – 3)
-
queue_put_limit – создать новый поток внутри функции queue_put, если число активных потоков в группе меньше данного значения (по умолчанию – 0)
-
create_thread_limit – не создавать поток в функции create_worker, если число активных потоков в группе превышает данное значение (по умолчанию – 1)
-
listener_wake_limit – не будить idle-поток в потоке listener, если число активных потоков в группе превышает данное значение (по умолчанию – 0)
-
listener_create_limit – не создавать новый поток в потоке listener, если число активных потоков в группе превышает данное значение (по умолчанию – 1).
Структура модели в виде графа взаимных вызовов методов классов приведена на рис.4. Названия методов даны в таблице 2. Основной цикл модели выглядит так (листинг 1).

Рис. 4. Структура имитационной модели
Таблица 2. Методы классов имитационной модели.
| Класс:: метод | Класс:: метод |
|---|---|
Threadpool::run |
12. Threadgroup::check_stall
|
Timer::run |
13. Threadgroup::queue_put
|
Threadpool::add_connection |
14. Threadgroup::queue_get
|
Threadgroup::run |
15. Connection::to_threading
|
Threadpool::check_stall |
16. Thread::to_polling
|
Threadgroup::add_connection |
17. Threadgroup::get_connection_from_polling
|
Threadgroup::assign_connection_to_thread |
18. Connection::to_usual_queue
|
Thread::to_active |
19. Thread::to_idle
|
Thread::to_waiting |
20. Connection::to_prio_queue
|
Connection::to_between |
21. Threadgroup::wake_thread
|
Threadgroup::listener |
22. Threadgroup::create_worker
|
Листинг 1.
#define NUMBER_OF_TACTS 60000000 /*in mcs */
int main() {
Threadpool *tpl = Threadpool::getInstance();
Timer *tmr = Timer::getInstance();
/*initialize random number generator*/
srand((unsigned)time(0));
for (long i = 0; i < NUMBER_OF_TACTS; i++) {
Tpl->run();
Tmr->run();
}
delete tpl;
delete tmr;
return 0;
}
Отдельно остановимся на вопросе, каким образом моделируются затраты времени CPU на переключение контекста процесса, т.к. именно по этой причине увеличение числа групп с некоторого момента приводит к деградации. Пусть – число активных потоков,
– число CPU, причем
,
– время переключения контекста (параметр модели),
– время обслуживания запроса (в терминах теории очередей – длина заявки). Тогда за 1 такт модельное время для всех заявок продвинется не на 1, а на величину
,
заявок выполнятся за время
и производительность равна
заявок в единицу времени, т.е. с ростом
она действительно снижается. Таким образом, формулируем правило: при выполнении условия
для всех активных потоков остаточная длина заявки уменьшается на величину
, в противном же случае действуем так: у произвольно взятых
из
активных потоков остаточную длину уменьшаем на единицу, у остальных
остаточная длина не изменяется. Второй случай соответствует ситуации, когда время переключения контекста слишком велико и использовать дисциплину разделения процессора не имеет смысла. Усеченные квадратные скобки в условии означают деление с округлением вверх.
Апробация модели и результаты
Валидность модели проверялась на контрольных примерах, где выходные результаты модели (производительность и средняя длительность исполнения запроса) сравнивались при той же моделируемой нагрузке с результатами, полученными на реальном сервере с помощью известной утилиты тестирования производительности MySQL sysbench. Модель показала расхождение с данными sysbench по обоим выходным параметрам в пределах 2%. В этом разделе мы рассмотрим результаты работы модели для двух принципиально различных профилей нагрузки – CPU-bound и IO-bound. Вот примеры различия во входных данных.
На рис. 5 и 6 показаны гистограммы для собранных данных (около 1000 наблюдений) для длительности одного раунда активности CPU в микросекундах. На рис. 7 и 8 показаны гистограммы для длительности одного раунда ожидания CPU (иными словами, нахождения потока в состоянии waiting). В первом случае (CPU-bound нагрузка) замеры производились для 1024 персистентных соединений с сервером при 32 ядрах, во втором случае (IO-bound нагрузка) – 128 соединений с более трудоемкими запросами при 64 ядрах. Из рисунков видно,
что длительность ожидания ввиду гораздо более значительного удельного веса операций
ввода-вывода в запросах во втором случае значительно выше. Это означает бОльшее время
простоя процессора и, соответственно, возможность эффективной установки размера трэдпула выше количества физических CPU.
На рис. 9 и 10 показаны зависимости производительности от размера трэдпула, построенные
с помощью имитационной модели. Продолжительность моделирования – 60 млн. тактов (микросекунд), т.е. 1 минута, количество CPU 72. Эти графики хорошо соответствуют известным паттернам такой зависимости, классифицированным, например, в [3]. Из графика видно, что при CPU-bound нагрузке размер трэдпула выше числа CPU не дает эффекта – процессоры и так постоянно загружены. Поэтому здесь основная цель модели – не столько максимизировать выход, сколько минимизировать размер трэдпула. Для IO-bound
нагрузки картина иная – производительность продолжает расти и после значения 72, достигая максимума при размере около 185, затем начинает снижаться из-за конкуренции потоков на CPU и затрат на смену контекста процесса.
 |
 |
| Рис 5. Длительность active-раунда для CPU-bound профиля | Рис 6. Длительность active-раунда для IO-bound профиля |
 |
 |
| Рис 7. Длительность wait-раунда для CPU-bound профиля | Рис 8. Длительность wait-раунда для IO-bound профиля |
 |
 |
| Рис 9. “concurrency level – throughput” для CPU-bound | Рис 10. “concurrency level – throughput” для IO-bound |
Заключение
Итак, где и каким образом можно применить построенную модель трэдпула – как для описанной в этой работе реализации, так и для любой другой:
-
Выявление настроек и локальных алгоритмических решений, к изменению которых производительность трэдпула наиболее чувствительна, и формирование на этой основе рекомендаций для инженера-проектировщика и администратора СУБД.
-
Выявление зависимости выходных величин от вида и параметров входных распределений.
-
Поиск оптимальных значений настроек и выявление их зависимости от количественных и качественных показателей нагрузки на сервер.
-
Динамическая оптимизация настроек трэдпула: по ходу работы трэдпула собирается и обрабатывается статистика, на основании которой периодически запускается модель для быстрого поиска оптимальных значений наиболее важных настроек.
-
Machine Learning: наполнение training data set, где представленному в количественном виде профилю нагрузки соответствует набор оптимальных параметров пула потоков. Этот data set далее можно будет использовать в реальной работе сервера СУБД для оптимизации пула потоков по собранному в run-time профилю.
Результаты применения имитационной модели будут продемонстрированы в последующих публикациях.
Список литературы
1: Better performance through threading. — developer.android.com/topic/performance/threads
2: Boer F.S., Grabe I., Jaghoori M.M., Stam A., Yi W. Modeling and Analysis of Thread-Pools in an Industrial Communication Platform. – ICFEM’09: Proceedings of the 11-th International Conference on Formal Engineering Methods, November 2009, pp.367-386.
3: Dongping X. Performance study and dynamic optimization design for threadpool systems (2004). – digital.library.unt.edu/ark:/67531/metadc780878/m2/1/high_red_d/835380.pdf
4: Fuentes E. Concurrency – Throttling Concurrency in the CLR 4.0 Threadpool
(September 2010). – docs.microsoft.com/en-us/archive/msdn-magazine/2010/September/concurrency-throttling-concurrency-in-the-clr-4-0-threadpool
5: Hellerstein J.L., Morrison V., Eilebrecht E. Applying Control Theory in the Real World. – ACM’SIGMETRICS Performance Evaluation Rev., Volume 37, Issue 3, 2009, pp. 38-42.
6: Hellerstein J.L., Morrison V., Eilebrecht E. Optimizing Concurrency Levels in the .NET Threadpool. – FeBID Workshop 2008, Annapolis, MD USA.
7: Ilinchik A. How to set an ideal thread pool size (April 2019). – engineering.zalando.com/posts/2019/04/how-to-set-an-ideal-thread-pool-size.html
8: Java Concurrency in lock optimization and optimization thread pool. -programmersought.com/article/84012626442
9: Nazeer S., Bahadur F. Prediction and Frequency Based Dynamic Thread Pool System. – Int. J. of Comp. Sci. and Information Security, Vol. 14, No. 5, May 2016, pp.299-308.
10: Oracle® GlassFish Server 3.1 Performance Tuning Guide. — docs.oracle.com/cd/E18930_01/pdf/821-2431.pdf
11: Pepperdine K. Tuning the Size of Your Thread Pool (May, 2013) – infoq.com/articles/Java-Thread-Pool-Performance-Tuning
12: Percona Server for MySQL: Thread Pool. — www.percona.com/doc/percona-server/5.7/performance/threadpool.html
13: Pyarali I., Spivak M., Cytron R. Evaluating and Optimizing Thread Pool Strategies for Real-Time CORBA. – ACM’SIGPLAN Notices, Volume 36, Issue 8, August 2001, pp.214-222.
14: Ronstrom M. MySQL Thread Pool: Summary (October 2011). — mikaelronstrom.blogspot.com/2011/10/mysql-thread-pool-summary.html
15: Stetsenko I., Dyfuchyna O. Thread Pool Parameters Tuning Using Simulation. – In book: Adv. in Comp. Sci. for Engineering and Education II (ed. Hu Z.), Springer 2020, pp.78-89.
16: Terrell R. Concurrency in .NET: Modern patterns of concurrent and parallel programming. – Simon and Schuster Publishing House, 2018, 568 pp.
17: Timm J. An OS-level adaptive thread pool scheme for I/O-heavy workloads. – Master thesis, Delft University of Technology, 2021 (repository.tudelft.nl)
18: Thread Pool in MariaDB. – mariadb.com/kb/en/thread-pool-in-mariadb
19: Warren M. The CLR Thread Pool ‘Thread Injection’ Algorithm (April 2017). – codeproject.com/Articles/1182012/The-CLR-Thread-Pool-Thread-Injection-Algorithm
20: github.com/dotnet/coreclr/blob/master/src/vm/win32threadpool.cpp
21: Акопян М.С. Расширение модели ParJava для случая кластеров с многоядерными узлами. – Труды ИСП РАН, том 23, 2012.
22: Бабичев С.Л., Коньков К.А., Коньков А.К. Использование пула вычислительных потоков со статическим планированием. – Труды МФТИ, т.4, № 3, 2012, с.162-170.
23: Клячин В.А. Реализация параллельного алгоритма геометрического хеширования на основе пакета NumPy и пула процессов. – Вестн. Волгогр. Гос. Ун-та, сер. 1, Мат.-Физ., 2015, выпуск 4 (29), с.13-23.
24: Труб И.И. Объектно-ориентированное моделирование на C++. –Питер, 2005. – 416с.

