Всем привет! Меня зовут Дима Лунин, и я аналитик в Авито. Как и в большинстве компаний, наш основной инструмент для принятия решений — это A/B-тесты. Мы уделяем им большое внимание: проверяем на корректность все используемые критерии, пытаемся сделать результаты более интерпретируемыми, а также увеличиваем мощность критериев. Про это всё мы уже написали две статьи на Хабр, вот первая часть, а вот — вторая.

В текущем посте я хочу рассказать, как ещё сильнее увеличить мощность критериев для A/B-тестирования, используя машинное обучение. В некоторых моментах буду ссылаться на две предыдущие статьи, так что если вы их ещё не читали, самое время это исправить.

Кратко, о чём я собираюсь рассказать:

1. Что такое CUPED-метод.

2. Как улучшить CUPED-алгоритм. CUPAC, CUNOPAC и CUMPED — подробно про каждый из них. 

3. Как использовать Uplift-модель в качестве статистического критерия. Здесь я продемонстрирую все прелести bootstrap-технологий.

4. Как использовать все модели сразу для достижения лучшей мощности.

5. Насколько эти методы вместе с парной стратификацией лучше, чем обычный CUPED.

Отдельно отмечу, что такие методы, как CUNOPAC, CUMPED, критерий на основе Uplift-модели и критерий, объединяющий несколько критериев, были разработаны и придуманы нашей командой.

Задачи для проверки критериев

Прежде чем приступить к рассказу о критериях, хочу показать, для каких задач годятся описанные далее алгоритмы.

Поюзерные A/B-тесты. Здесь вы одним пользователям показываете новый дизайн, новые фишки и так далее, а в другой группе оставляете всё как было. Ждёте какой-то срок и смотрите с помощью статистического критерия, прокрашен тест или нет.

Конечно, в таких экспериментах хочется иметь наиболее мощный критерий: так мы сможем проверить больше гипотез за меньшее время. Ещё примеры, зачем может потребоваться большая мощность у критерия, можно найти в статьях выше.

Но бывают случаи, когда такое не получается сделать. Например, вы тестируете новую рекламу на билбордах или телевидении. Тогда вы не можете одним пользователям в Москве показывать новую рекламу, а вторым в этот момент завязать глаза.

То же самое с новыми продуктами. Мы в Авито тестировали в своё время новые услуги продвижения. Если бы мы проводили обычный поюзерный A/B-тест, то в поисковой выдаче были бы два типа объявлений: с новыми услугами продвижения и со старыми. И это нарушило бы чистоту эксперимента: при раскатке у нас все объявления будут с новыми услугами в поисковой выдаче, а результаты A/B мы получили на смешанной поисковой выдаче. Здесь поможет другой тип экспериментов.

Региональные A/B-тесты. Давайте перейдём к новой статистической единице — региону. Например, будем показывать нашу рекламу или введём новые услуги только в половине регионов России. Тогда всё честно: рекламу в одном регионе не увидят пользователи из других регионов (а точнее число тех, кто увидит, будет пренебрежимо мало). И выдача объявлений не пересекается по регионам. Так что пользователям Ростовской области можно разрешить купить новые услуги продвижения, а в Краснодарском крае — нет, они друг на друга не влияют.

С точки зрения математики это означает, что вместо гигантского количества пользователей в A/B-тесте у нас будет примерно 85 элементов-регионов: 42 из них — в тесте и 43 — в контроле. В этом случае мы также можем применять статкритерии, которые используются для поюзерных экспериментов. Но элементов всего 85, нормально ли они себя покажут? Не будут ли критерии строить некорректный доверительный интервал?

Главный минус таких тестов — они слишком шумные. Чтобы задетектировать хоть какой-то эффект, надо, чтобы он был огромным. Поэтому если будет алгоритм, который сможет очень сильно увеличить мощность критерия, или, что эквивалентно, сократить доверительный интервал для эффекта, это будет мегаполезно для бизнеса.

На этих двух задачах я и буду тестировать все представленные далее критерии и на них же покажу результаты. Теперь предлагаю перейти к сути статьи. Начнём с CUPED-алгоритма.

CUPED

CUPED (Controlled-experiment Using Pre-Experiment Data) — очень популярный в последнее время метод уменьшения вариации. Чтобы понять, как он работает, рассмотрим искусственный пример.

Пусть ваша метрика — выручка, и эксперимент длится месяц. Вы собрали данные во время эксперимента, какая выручка от пользователей в тесте и в контроле:

В итоге метрики очень шумные: в тесте даже на трёх точках видно, что значения разнятся от 50 до 150, а в контроле — от 20 до 200 рублей. С помощью T-test получились следующие результаты: +10±20 ₽ на одного пользователя, результат не статзначим. Как это исправить?

Давайте добавим информацию с предпериода: сколько эти пользователи тратили в среднем в месяц до начала эксперимента. При правильном сетапе теста матожидание этой величины одинаково в тесте и в контроле. Тогда:

Будем теперь смотреть на дельту. Это разница выручки на экспериментальном периоде минус средняя выручка на предпериоде в месяц.

Во-первых, почему так можно? В тесте и в контроле мы вычитаем с точки зрения матожидания одно и то же, потому что в правильно проведённом A/B-тесте контроль и тест ничем не отличаются на предпериоде. Поэтому, когда мы смотрим на разницу, эти вычитаемые величины нивелируются.

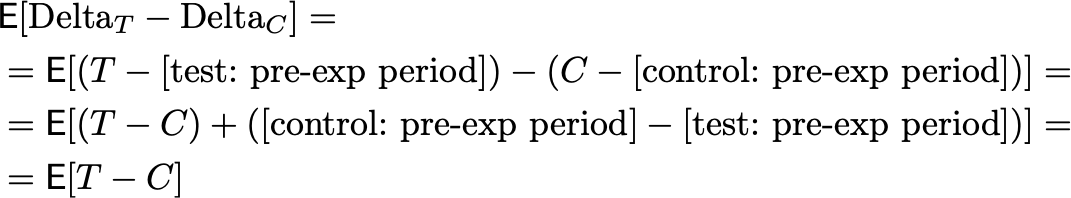
Здесь:

• T — экспериментальная метрика в тесте.

• C — экспериментальная метрика в контроле.

Во-вторых, зачем нам всё это?

Посмотрим на разброс значений в delta: в контроле от -10 до 6 рублей, а в тесте от -10 до 20 рублей. Это намного меньше того разброса, что мы видели ранее. Поэтому и доверительный интервал сократится: результат станет +15±5 ₽ для одного пользователя, и он уже статзначим! Почему дисперсия уменьшилась? Потому что мы смогли объяснить часть данных в эксперименте с помощью предпериода. 

А теперь посмотрим на CUPED более формально. 

Основная идея CUPED-метода: давайте вычтем что-то из теста и из контроля так, чтобы матожидание разницы новых величин осталось таким же, как и было. Но дисперсия при этом уменьшилась бы:

Где A и B — некоторые случайные величины (ковариаты). Тогда утверждается, что если θ будет такой, как указано в формулах далее, то дисперсия будет минимально возможной для таких статистик.

В примере выше θ я взял равной 1, но на самом деле, лучше было подобрать значение по этой формуле. Тогда формула для дисперсии получается такой:

Поэтому, чем больше корреляция по модулю, тем меньше будет дисперсия.

Также важно помнить: чтобы метод работал корректно, достаточно, чтобы матожидания A и B совпадали:

Ещё больше интересных и нетривиальных моментов про CUPED расписано в прошлой статье. В частности, там есть информация о том, как построить относительный CUPED-критерий.

Осталось понять, что брать в роли A и B. Чаще всего для них берут значения той же метрики, но на предэкспериментальном периоде. В примере выше мы брали среднюю выручку за месяц. Чем хорош такой способ:

1. Матожидание метрики на предпериоде будет одним и тем же в тесте и в контроле — иначе у вас некорректно поставлен A/B-тест. А значит, CUPED даст правильный результат.

2. В большинстве случаев метрика на предпериоде сильно коррелирует с экспериментальным периодом. Отсюда получается, что и дисперсия сильно уменьшится.

Но кроме значения метрики на предпериоде можно использовать результаты ML-модели, обученной предсказывать истинные значения метрик без влияния тритмента. С хорошей моделью можно достичь большего уменьшения дисперсии. Давайте поговорим о том, как это сделать.

CUPAC

CUPAC (Controlled-experiment Using Prediction As Covariate) — первая вариация на тему CUPED с ML. Как я уже писал выше, давайте попробуем использовать предсказание в качестве ковариаты. Распишу сам предлагаемый алгоритм на примере определённой задачи. Для ваших задач вы сможете переиспользовать алгоритм по аналогии.

Пусть у нас есть A/B-тест, где:

• Дата начала — 1 июня.

• Длительность теста составляет 1 месяц.

• Наша ключевая метрика — выручка.

• 1 месяц уже прошёл.

Чтобы оценить такой тест, мы проделаем следующую операцию из трёх основных шагов:

1. Соберём датасет для предсказания (или «экспериментальный датасет») и обучения.

2. На обучающем датасете обучим нашу модель, подберём гиперпараметры, а на экспериментальном будем предсказывать таргет, используя фичи с предпериода.

3. Мы получили новую ковариату и запускаем обычный CUPED-алгоритм.

На схеме это можно изобразить так:

Как собрать экспериментальный и обучающий датасеты?

На иллюстрации сине-красный датасет — экспериментальный, а бирюзовый — обучающий, собранный до 1 июня. Одним цветом отмечено, что пользователи друг от друга в среднем ничем не отличаются, разными цветами — между ними есть разница.

Теперь опишем сам алгоритм в тексте. Повторим в цикле, пока не жалко:

1. Вычитаем из текущей даты длительность эксперимента. Начинаем с 1 июня, потом получим дату 1 мая, потом — 1 апреля и так далее.

2. Теперь собираем таргет. Для каждого юзера сохраняем его суммарные траты у нас на сайте за этот месяц. Для 1 июня это экспериментальная выручка за июнь (и уже за июнь вся выручка известна), для мая это выручка за май, когда ещё не было никаких отличий между тестом и контролем, и так далее.

   • Тут у нас получатся один сине-красный датасет с экспериментальной выручкой (и она отлична у теста с контролем) и много бирюзовых датасетов, где пользователи в среднем неразличимы.

3. И теперь собираем датасет фичей. Главная особенность состоит в том, что фичи должны быть собраны до текущей рассматриваемой даты. То есть для 1 июня все фичи должны быть собраны по данным до 1 июня, аналогично для остальных дат.

   • Например, количество заходов на сайт за N месяцев до рассматриваемой даты (за 2 месяца до 1 июня; за 2 месяца до 1 мая и так далее).

   • Выручка от пользователя за разные промежутки времени (за 1 месяц, за 2 месяца и так далее).

   • Сколько месяцев назад зарегистрировался пользователь.

4. Ни в одном из датасетов нет фичи тестовая или контрольная группа. Важно, чтобы пользователи по обучающим фичам в тесте и в контроле были полностью идентичны.

Что важно проверить: нужно, чтобы матожидания новых ковариат совпадали. А для этого достаточно, чтобы признаки ML-модели в среднем не отличались в тесте и в контроле. Далее идёт теоретическое пояснение этому факту.

Теоретическое пояснение

Обозначим X и Y — фичи пользователей в тесте и в контроле. То есть наша случайная величина — это вектор фичей. Тогда, если тест и контроль подобраны корректно (случайно или с помощью парной стратификации):

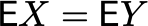
Что произойдет, когда мы обучим модель? Она просто преобразует вектор признаков одного пользователя в число с помощью некоторой функции F. Тогда: 

Обозначим A := F(X), B := F(Y). Тогда, как я писал выше в CUPED, метод будет корректен.

Вот и всё! Это полный пайплайн работы CUPAC-алгоритма. Теперь я попытаюсь объяснить, зачем нужен тот или иной шаг.

Вопросы и ответы к методу

Зачем нужен обучающий датасет?

Чтобы не было переобучения. Если объяснять простыми словами, то это приводит к тому, что доверительный интервал заужается и становится некорректным. И ошибка первого рода будет не 5, а, например, 15%. А теперь поподробней.

Допустим, мы бы обучались прямо на экспериментальном датасете и на нём же предсказывали. Рассмотрим пример:

Пусть у нас есть один признак для обучения, и функция выручки пользователя зависит от признака рыжей линией на рисунке. Допустим, мы возьмём какую-то легко переобучаемую модель: например, полином 10-й степени. Обучим её на синих точках-примерах (экспериментальном датасете в терминах CUPAC). В таком случае текущая модель практически идеально предскажет их значения.

Подставим в CUPED предсказание, получим эффект 0 и дисперсию 0, потому что модель везде всё верно предсказала. Имеет ли это какое-то отношение к реальной картине? Нет! Видно даже, что в реальности синие точки не лежат на рыжей линии, а значит, некоторый шум в данных точно есть.

Мы видим, что в других точках, где модель не обучалась, она ведёт себя совершенно не так, как истинная функция выручки. Это значит, что если бы мы насемплировали другую выборку пользователей, то эффект и дисперсия в CUPED были бы другими! Итого, мы обучились не на генеральную совокупность, а на частичный, увиденный в обучении, пример. Это и есть проблема переобучения.

Почему нельзя собирать обучающие фичи на том же периоде, на котором мы и предсказываем?

Во время эксперимента так делать нельзя, потому что мы могли повлиять на этот признак тестируемым тритментом. И тогда фичи в тесте и в контроле будут различны в этих группах, а полученные на таких данных ковариаты будут иметь разное матожидание в зависимости от группы. А значит, CUPED применять нельзя.

На обучающем датасете мы тоже не можем использовать такие признаки, потому что тогда обучающий и экспериментальный датасеты будут различны по структуре.

Зачем лезть так далеко в историю? Не достаточно ли для обучающего датасета взять датасет, собранный, например, для 1 мая? 

В принципе, такой вариант подойдёт, но чем больше обучающий датасет, тем лучше обучится модель. Плюс мы можем добавить временные признаки в качестве обучающих фичей: номер года, категорийную фичу месяца, сезон.

А что, если наша метрика — конверсия?

Так вместо задачи регрессии у нас задача классификации. И можно использовать вероятность модели в качестве ковариаты. При этом можно точно также оставить регрессионную модель.

Как обучать модель?

Об этом я расскажу дальше.

Про результаты работы критерия: как и ранее, я буду сравнивать алгоритмы по метрике «ширина доверительного интервала». Чем она меньше, тем лучше.

• На поюзерных тестах: уменьшение доверительного интервала на 1000 A/A-тестах в среднем на 4% относительно CUPED.

• На региональных тестах: уменьшение доверительного интервала на 1000 A/A-тестах  в среднем на 22% относительно CUPED.

Если вы решите реализовать этот или любой другой алгоритм из статьи, то обязательно проверьте его корректность!

Это всё, что здесь можно рассказать. Теперь перейдём к «нечестному» CUPAC и избавимся от большинства шагов в алгоритме.

CUNOPAC

CUNOPAC (Controlled-experiment Using Not Overfitted Prediction As Covariate) — чуть более простая, чуть менее корректная и чуть более мощная модель, чем CUPAC. В вопросах к CUPAC я писал, что обучающий датасет нам нужен, ведь иначе может возникнуть проблема переобучения. Но я предлагаю забыть про эту проблему!

Главное, о чём надо помнить в таком случае — вы можете построить некорректный критерий! Он будет строить зауженный доверительный интервал, и вместо 95% случаев будет покрывать лишь 85%. Но об этом я расскажу далее.

Алгоритм работы критерия такой:

1. Соберём экспериментальный датасет для предсказания.

2. На нём обучим нашу модель, подберём гиперпараметры, и на нём будем предсказывать таргет, используя фичи с предпериода. Обучаемся на всем датасете сразу! И предсказываем весь датасет. Ничего не откладываем на валидацию (да, метод рискованный).

3. Мы получили новую ковариату и запускаем обычный CUPED-алгоритм.

На схеме это можно изобразить так:

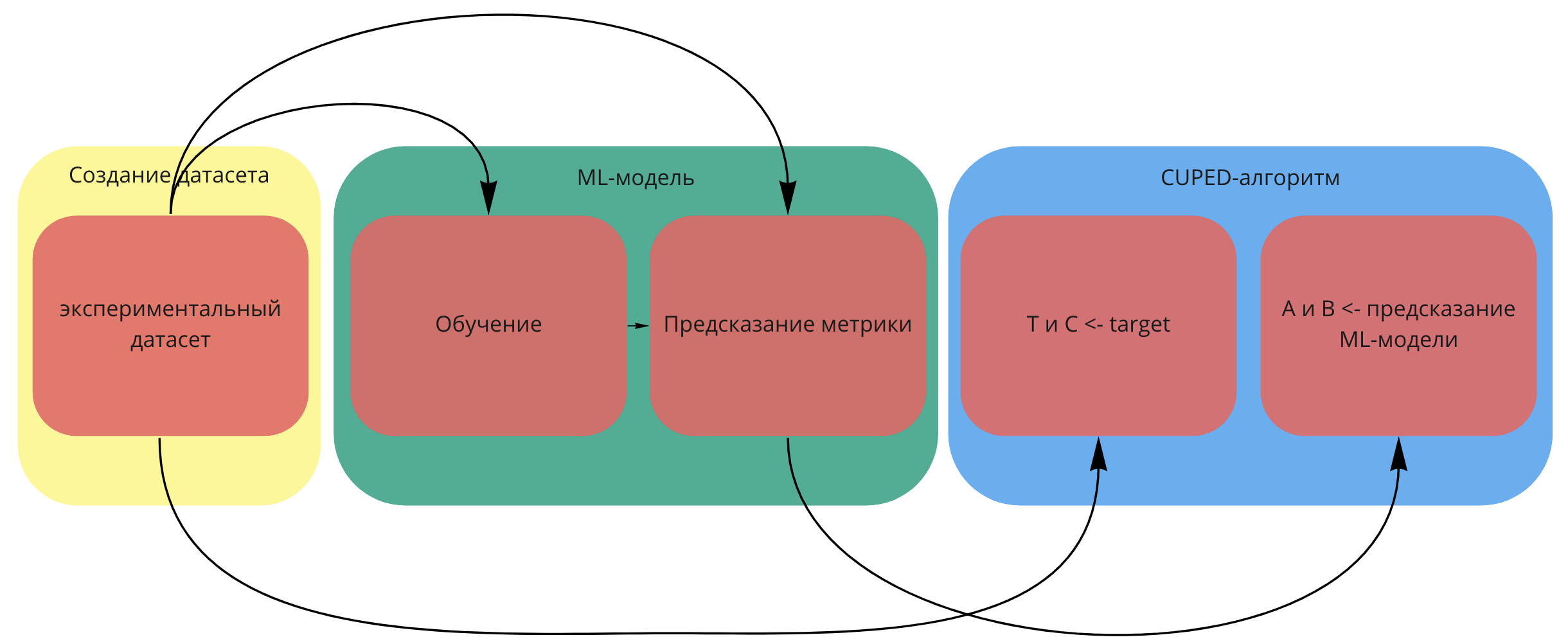
Датасет собираем также, как и в CUPAC-алгоритме, только обучающий датасет больше не нужен:

Теперь вопрос: как подобрать модель, которая не переобучится? Мы решили этот вопрос так: отбираем небольшое количество фичей и используем только линейные модели.

Рассмотрим пример: что, если взять CatBoost-алгоритм или линейную регрессию в качестве ML-алгоритма внутри критерия? Посмотрим на реальный уровень значимости (или False Positive Rate), полученный при проверке метода на 1000 А/А-тестах:

• Линейные модели: 0.055 (при alpha=0.05), результат статзначимо не отличается от теоретического alpha.

• CatBoost: 0.14 (при alpha=0.05), результат статзначимо отличается от теоретического alpha!

То есть CatBoost ошибается примерно в 3 раза чаще, чем должен был! Он переобучается, заужает доверительный интервал и поэтому критерий некорректен. Что это значит на практике? Что вы в 3 раза чаще будете катить изменение, которое на самом деле не имеет никакого эффекта. Поэтому CatBoost нельзя использовать внутри CUNOPAC, а линейные модели можно. При этом я не говорю, что CatBoost плохой алгоритм! Он отличный, просто он легче переобучается.

Есть ли переобучение у линейной модели? Наверняка есть, но оно настолько мало, что не влияет на эффект.

А почему качество CUNOPAC лучше, чем у CUPAC?

Возникает вопрос: а почему качество может стать лучше, чем у CUPAC?

1. В предыдущей модели CUNOPAC мы обучаемся на исторических данных, и в этот момент не учитываем текущие тренды и сезонность, а в текущей CUNOPAC эти недостатки убраны.

2. Наша цель — найти наиболее скоррелированную метрику с T-C, ведь в таком случае дисперсия уменьшится максимально возможным способом. А так как в CUPAC при обучении вообще никак не участвует метрика T (а лишь значения метрики без какого-либо тритмента), то результат вполне ожидаемо будет менее скоррелирован, чем у модели, которая обучалась в том числе и на значениях метрики T. Поэтому, качество у CUNOPAC должно быть лучше, чем у CUPAC.

3. Ну и наконец, как показали наши эксперименты, в CUPAC лучше всего также сработали линейные модели (что было для нас удивительно, бустинги и деревья показали себя хуже). CUNOPAC дал буст по качеству, так как тоже использует линейные модели.

Что ещё хочется отметить: это очень опасная модель! Если модель переобучиться, вы будете заужать доверительный интервал и ошибка будет больше заявленной. Поэтому снова предупреждаю: обязательно проверьте ваш критерий!  

Результаты работы критерия:

• На поюзерных тестах: уменьшение доверительного интервала на 9% относительно CUPED.

• На региональных тестах: не удалось использовать, реальный уровень значимости сильно больше тестируемых 5%, слишком мало регионов. Модель просто всегда переобучается.

Проверено на 1000 A/А-тестах.

А теперь обсудим, как построить пайплайн обучения модели для этих двух критериев.

Автоматизация ML-части критериев

Поговорим про основную часть алгоритмов. Что у нас есть: обучающий и экспериментальный датасеты, которые мы будем скармливать модели. В случае CUNOPAC это один и тот же датасет. Расскажу, как я воплотил ML-часть алгоритмов, но это не значит, что у меня получилась идеальная автоматизация: возможно, вы сможете придумать лучше. При этом, если вы плохо понимаете идеи и алгоритмы машинного обучения, то можете пропустить эту часть. Она никак не повлияет на осознание всех алгоритмов далее.

Краткая иллюстрация:

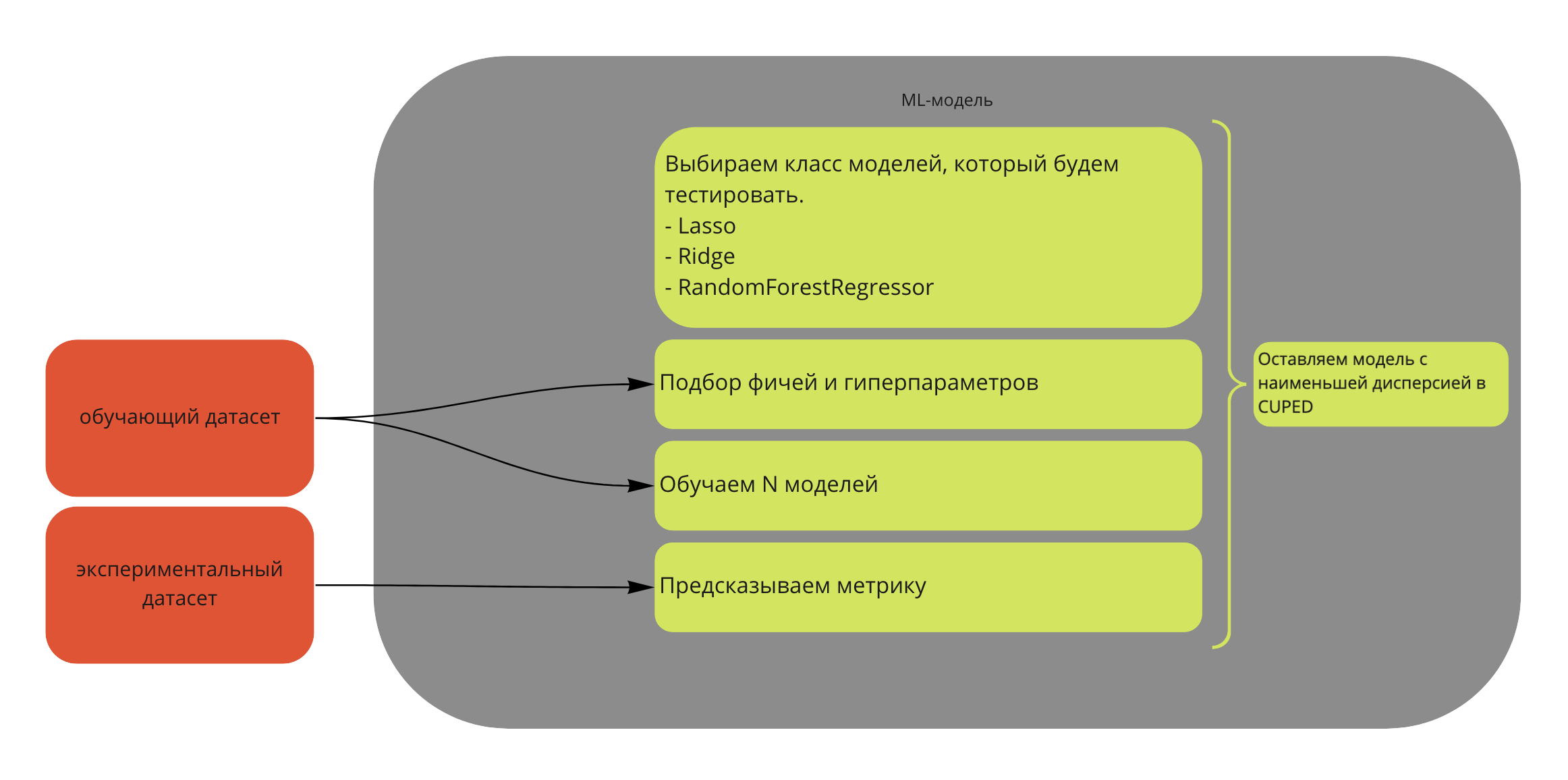
Шаг 1. Выбираем класс моделей, который будем тестировать. Например, я использовал:

Для CUPAC: Lasso, Ridge, ARDRegression, CatBoostRegressor, RandomForestRegressor, SGD, XGBRegressor.

Для CUNOPAC: Lasso, ARDRegression, Ridge.

Дополнительно: для адекватности я нормирую все признаки с помощью StandardScaler.

Шаг 2. Выбираем фичи для обучения. Ограничим сверху количество используемых фичей и воспользуемся одним из алгоритмов подбора признаков:

1. Жадный алгоритм добавления/удаления признаков (например, SequentialFeatureSelector из библиотеки scikit-learn на Python).

2. Алгоритм на основе feature_importance параметра фичей у модели (SelectFromModel из библиотеки scikit-learn на Python). Самый быстрый из алгоритмов.

3. Add-del алгоритм (добавляем фичи, пока качество улучшается, потом выкидываем фичи, пока качество улучшается, повторим процедуру снова, пока не сойдёмся).

4. Всё, что ещё найдёте или придумаете.

Единственное замечание: если у алгоритма отбора фичей можно задать функцию оценки для качества модели, то стоит использовать специальную функцию-скоррер:

def cuped_std_loss_func(y_true, y_pred):
    theta = np.cov(y_true, y_pred)[0, 1] / (np.var(y_pred) + 1e-5)
    cuped_metric = y_true - theta *  y_pred
    return np.std(cuped_metric)

Так вы будете оценивать ровно ту величину, которую вы хотите оптимизировать — ширину доверительного интервала у CUPED-метрики.

Шаг 3. Следующая остановка — выбор гиперпараметров. Мы считаем в этот момент, что все обучающие признаки уже выбраны. Есть следующие варианты:

1. Перебор по GridSearchCV.

2. Перебор по RandomizedSearchCV.

3. Жадный перебор по одному параметру:

   • сначала подбираем по функции cuped_std_loss_func первый в списке гиперпараметр;

   • потом подбираем второй в списке, при учёте выбранного первого гиперпараметра и т.д. Пример с кодом:

start_params = {
    'random_state': [0, 2, 5, 7, 229, 13],
    'loss': ['squared_loss', 'huber'],
    'alpha': np.logspace(-4, 2, 200),
    'l1_ratio': np.linspace(0, 1, 20),
} # Пример перебора параметров для SGD
def create_best_model_with_grid_search(pipeline, start_params, X, y):
        final_params = {}
        params = []
        for param in start_params.items():
            params_dict = {}
            params_dict[param[0]] = param[1]
            params.append(params_dict)
         
        score = make_scorer(cuped_std_loss_func, greater_is_better=False)
        for param in params:
            search_model = GridSearchCV(pipeline, param, cv = 2, n_jobs = -1,
                                        scoring = score)
            search_model.fit(X, y)
            final_params = {**final_params, **search_model.best_params_}
            pipeline.set_params(**final_params)
        return pipeline, final_params

Плюс такого метода: скорость по сравнению с первым методом. Вместо всех возможных комбинаций здесь перебирается линейное количество вариантов. Все значения гиперпараметров будут рассмотрены по сравнению со вторым методом.

Минус: GridSearchCV даст лучшее качество, но работать будет сильно дольше.

Ещё, конечно, можно объединить предыдущий шаг с этим: для каждого набора фичей подобрать гиперпараметры и измерять качество по cuped_std_loss_func. Но это работает очень долго. Можно также устроить сходящуюся процедуру из этих двух шагов: выбираем признаки, выбираем гиперпараметры, снова выбираем признаки с подобранными значениями гиперпараметра и так далее.

Шаг 4. Отлично, после обучения у нас есть N моделей с первого шага с подобранными гиперпараметрами и обучающими признаками для каждой из них. Отберём из них одну модель, которая даёт наилучшее качество на экспериментальном датасете по cuped_std_loss_func. Почему так можно сделать, я расскажу, когда буду описывать Frankenstein-критерий. 

А пока перейдём к третьему критерию, который, грубо говоря, не является ML-критерием.

CUMPED

Почему нам вообще нужна только одна ковариата? Почему нельзя использовать сразу N ковариат? Именно на этой идее построен алгоритм CUMPED (Controlled-experiment Using Multiple Pre-Experiment Data).

Ранее в CUPED было так:

А теперь в CUMPED будет так:

При этом не обязательно использовать только две ковариаты, их может быть сколько угодно!

Зачем нам вообще может потребоваться N ковариат? Почему одной недостаточно?

Как я писал в CUPED-алгоритме, из-за того, что часть метрик T и C описывается данными из ковараиты, мы и сокращаем дисперсию. А если признаков будет не один, а сразу несколько, то мы лучше опишем нашу метрику T и C, а значит сильнее сократим дисперсию. Это то же самое, что и в машинном обучении: что лучше, использовать один признак для обучения или несколько различных фичей? Обычно выбирают второе.

Теперь опишем первую версию предлагаемого алгоритма CUMPED:

1. Соберём один экспериментальный датасет, как сделали это в CUNOPAC.

2. В цикле по всем признакам, которые использовались ранее для предсказания метрики:

   • Образуем CUPED-метрику T', С', используя в качестве ковариат текущие признаки в цикле.

   • В следующий раз в качестве изначальных метрик будут использоваться новые CUPED-метрики. То есть на следующей итерации цикла вместо текущих метрик T и C будут использоваться полученные сейчас T', C'.

Если расписать формулами, то:

Где наша итоговая CUMPED-метрика это T^N, C^N, а A_i, B_i — это признаки пользователя, собранные на предпериоде. Раньше мы на них обучали модель, а сейчас используем в качестве ковариат. Коэффициенты тета подбираются следующим образом:

Вот и весь алгоритм. Но! Если бы вы его реализовали, то он, вероятно, показал бы себя хуже, чем обычный CUPED-алгоритм. Почему?

В этом алгоритме есть одна беда:

Порядок применения ковариат важен! Если сначала вычесть ковариату A_1, а потом ковариату А_2, то дисперсия может быть больше, нежели в случае, когда вы сначала вычтете A_2, а потом A_1.  Вы можете сами расписать формулы, и увидеть, что две эти случайные величины будут иметь разную дисперсию.

Поэтому предлагается применять ковариаты в «жадном» порядке: сначала ищем наилучшую ковариату, уменьшающую дисперсию сильнее всего, потом следующую ковариату, уменьшающую дисперсию лучше всего для T^1, C^1  и т. д. То есть в первой версии алгоритма мы берём не случайную ковариату, а ту, которая на текущий момент сильнее всего уменьшает доверительный интервал.

На рисунке представлен итоговый алгоритм CUMPED:

Иллюстрация подбора наилучшей ковариаты:

Вопросы и ответы к методу

Можно ли подобрать коэффициенты theta_1, theta_2, ... theta_N в алгоритме неким другим способом, чтобы дисперсия была меньше?

Да, можно. Текущий алгоритм не является оптимальным, потому что если решать задачу,

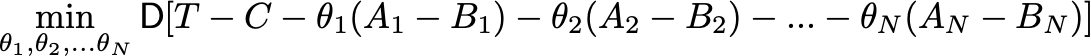
то оптимум у коэффициентов будет другим! Но для этого надо взять производную N раз по каждой theta, приравнять производные к 0 и решить N уравнений относительно N неизвестных. Не самая приятная задача, хотя есть методы, которые могут численно найти ответ для неё. Также я не считаю, что дисперсия в таком решении сильно уменьшится относительно того, что я получил описанным жадным алгоритмом. Я не реализовывал такой вариант, так что буду рад, если кто-то решит сравнить эти два алгоритма.

А алгоритм может остановиться? Если признаков в обучающем датасете будет бесконечно много, то как понять, что пора остановиться?

Никак. Если посмотреть на CUPED-алгоритм, то дисперсия в новых CUPED-метриках не больше изначальной дисперсии. Поэтому в теории можно использовать бесконечно много ковариат, просто большинство из них будут иметь нулевой коэффициент theta.

На практике всё не так радужно: к сожалению, мы не знаем истинной ковариаты, а лишь её состоятельную оценку, полученную на текущих данных. А оценка, как известно, практически всегда отличается от настоящего значения. Поэтому в реальности посчитанный коэффициент theta в алгоритме всегда будет не нулём, и мы всё время будем уменьшать выборочную дисперсию, даже если метрика и ковариата не скоррелированны. А это может привести к тому, что мы заузим доверительный интервал. А значит и ошибка первого рода будет больше заявленной.

В качестве примера рассмотрим на искусственных данных первый шаг алгоритма: насколько он уменьшит дисперсию. Пример будет показан на одновыборочном CUPED-критерии.

import scipy.stats as sps
import numpy as np
import seaborn as sns
 
sample_size = 100
 
sample = sps.norm(scale=10).rvs(sample_size)
 
cumpled_std_samples = []
# генерируем эксперимент 100 раз, чтобы получить какое-то распределение для оценки дисперсии
for _ in range(100):
    # истинная оценка стандартного отклонения
    estimated_mean_sample_std = np.std(sample) / np.sqrt(sample_size)
    # признаки-ковариаты в CUMPED, никак не скоррелированны с sample
    feature_matrix = sps.norm().rvs((5000, sample_size))
    # 1 шаг алгоритма
    for covariate in feature_matrix:
        # CUPED part
        theta = np.cov(sample, covariate)[0, 1] / np.var(covariate)
        sample_std = np.std(sample - theta * covariate) / np.sqrt(sample_size)
         
        # Выбор наилучшей ковариаты по уменьшению std у CUPED-метрики. Первый шаг алгоритма.
        if sample_std < estimated_mean_sample_std:
            estimated_mean_sample_std = sample_std
    cumpled_std_samples.append(estimated_mean_sample_std)
 
sns.distplot(cumpled_std_samples)

Получилось, что оценка алгоритмом стандартного отклонения в каждом случае из 100 была меньше теоретического значения 1 — стандартное отклонение равно 10, а размер выборки равен 100, значит стандартное отклонение для среднего равно 1. А это лишь первый шаг алгоритма!

А теперь хорошие новости: чем больше выборка, тем меньше будет это различие. Рассмотрим на примере, когда размер выборки равен 10000. В этом случае мы всё также будем заужать дисперсию, но в процентном соотношении сильно меньше: например в случае, когда выборка была размера 100, средний процент заужения доверительного интервала составлял 8%. А когда выборка стала размером 10000, то процент заужения относительно истинного стандартного отклонения составил 0,1%!

Поэтому во втором случае заужением доверительного интервала можно пренебречь: ничего плохо не произойдёт. Да, возможно ошибка первого рода будет не 5%, а 5,1%, но это и не страшно. Плюс в реальности размеры выборок чаще всего ещё больше.

Итого, исходя из вышесказанного, CUMPED отлично работает в случае, если выборка большого размера: и с точки зрения теории, и на проведенных 1000 A/A-тестах. То есть на поюзерных тестах его можно использовать. Но на региональных тестах с ним надо быть осторожным: в нашем случае он заработал только тогда, когда мы ограничили количество шагов алгоритма до 1.

Результаты работы критерия:

• На поюзерных тестах: уменьшение доверительного интервала на 14% относительно CUPED. Это наилучший результат среди всех представленных здесь алгоритмов.

• На региональных тестах: уменьшение доверительного интервала на 21% относительно CUPED. Но можно использовать лишь одну ковариату! Почему так, я ответил в скрытом разделе с вопросами.

Проверено на 1000 A/А-тестах.

Uplift-критерий

Всё, забыли про CUPED и всё, что с ним связано. В этом разделе я покажу, как из Uplift-модели сделать настоящий критерий. Но для начала о том, что такое Uplift-модель.

Давайте соберём датасет так же, как ранее это делали в CUNOPAC и в CUMPED, но в этот раз добавим фичу: какая группа пользователя. 1 — пользователь в тесте, 0 — в контроле.

Теперь посмотрим, как работает алгоритм:

1. Разделим датасет на K частей.

2. Будем в цикле размера K выбирать часть пользователей, которым будем предсказывать их метрику. На оставшейся части обучим ML-алгоритм. Эти два шага в ML зовутся кросс-валидацией.

3. Теперь для каждого пользователя на тестовой части предскажем его выручку, если бы он был в тесте и если бы он был в контроле. Как мы это сделаем? Поменяем в датасете фичу группы пользователя: на 1, если предсказываем выручку от него в тесте, и на 0, если предсказываем его выручку в контроле. Обозначим эти значения T_p и C_p. Теперь оценка Uplift для пользователя — это предсказанная выручка, если пользователь в тесте минус предсказанная выручка, если пользователь в контроле.

4. Повторим K раз и получим Uplift для всех пользователей.

На рисунке я кратко описал то же самое. Возможно, так будет понятней:

Мы смогли получить численную оценку эффекта для каждого пользователя. Однако есть несколько «но»:

1. Как из оценки построить доверительный интервал?

2. А если модель смещённая или некорректная? Например, она никак не учитывает группу пользователя внутри себя: тогда Uplift будет равен 0, что может быть не так. А если для тестовых юзеров он постоянно занижает предсказание, а для контрольных юзеров завышает?

Чтобы решить обе проблемы, введём ошибку предсказания:

Тогда:

То есть наш Uplift будет равен разнице предсказаний + разнице ошибок предсказаний в тесте и в контроле. Отличие по сравнению со старой формулой в том, что теперь мы добавляем ошибку предсказания: если мы занижаем предсказание на тестовых юзерах, то ошибка предсказания на тесте будет положительной. То же самое для контрольных юзеров.

Тогда численную оценку Uplift можно представить следующим образом:

Но и здесь есть проблема: размер выборок у трёх слагаемых разный! Давайте посмотрим, а что мы вообще можем посчитать для каждого пользователя.

Для пользователя в тесте:

• Значение метрики в тесте (или T в формулах выше).

• Предсказание модели, если пользователь в тесте (или T_p в формулах выше).

• Предсказание модели, если пользователь в контроле (или C_p в формулах выше).

• Ошибку предсказания модели, если пользователь в тесте (или ε_T в формулах выше).

Для пользователя в контроле:

• Значение метрики в контроле (или C в формулах выше).

• Предсказание модели, если пользователь в тесте (или T_p в формулах выше).

• Предсказание модели, если пользователь в контроле (или C_p в формулах выше).

• Ошибку предсказания модели, если пользователь в контроле (или ε_C в формулах выше).

Поэтому, размер выборок на самом деле будет таким:

• T_p, С_p: их размер равен количеству пользователей в тесте и в контроле, или |T| + |C| .

• ε_C: размер этой выборки равен количеству пользователей в контроле, или |C|.

• ε_T: размер выборки равен количеству пользователей в тесте, или |T|.

Вкратце это выглядит так:

Выпишем формулу Uplift с учётом всех вводных:

Так, а теперь вопрос. Как для такой статистики построить доверительный интервал? Ведь T_p, C_p, ε_T, ε_C ещё и коррелируют между собой? Как я упоминал в предыдущих статьях, если не знаете, как что-то посчитать теоретически, то используйте bootstrap. В данном случае достаточно забутстрапить каждого пользователя в тесте и в контроле по отдельности, а точнее их метрики T_p, С_p, ε_C, ε_T. Далее на каждой итерации внутри бутстрапа посчитаем оценку Uplift для них по формуле выше, и по этим данным построим доверительный интервал.

Замечание

В предложении выше есть небольшой подвох: на самом деле, мы должны не просто забутсрапить пользователей, но и каждый раз заново обучать модель. Когда мы обучаем модель, наши предсказания на тесте становятся зависимыми от пользователей в обучении. Если мы обучимся на одних пользователях, то предсказание будет одно, а если на других, то предсказание изменится.

Поэтому, по логике работы бутстрапа, когда мы бутстрапим пользователей для построения доверительного интервала, мы должны использовать не те значения, которые были посчитаны в первый раз на изначальном датасете, а заново обучить модель K раз (K — параметр кросс-валидации) и использовать новые метрики. 

Но на практике работает и описанный выше алгоритм, поэтому можете провести обучение один раз и не заморачиваться.

Результаты работы критерия:

• На поюзерных тестах: уменьшение доверительного интервала на 4% относительно CUPED.

• На региональных тестах: уменьшение доверительного интервала на 40% относительно CUPED. Это наилучший результат — обыгрывает CUPAC, CUMPED в 2 раза.

Почему произошло столь сильное сокращение на региональных тестах? Потому что на самом деле мы увеличили датасет в 2 раза. Если ранее размер выборки был примерно 42 на 43 (если регионов 85), то сейчас, так как модель предсказывает значения в тесте и в контроле для каждого региона, размер датасета стал 85 на 85. Есть, конечно, оговорка, что мы так увеличили только T_p и C_p, но как видим, это отлично работает.

Проверено на 1000 A/А-тестах.

Frankenstein-критерий

Вот у нас есть четыре критерия, а когда какой стоит использовать? Ранее я писал, что CUMPED лучше всего работает для поюзерных тестов, а Uplift — для региональных. А зачем я рассказывал про все остальные? Но ведь они лучше всего работают в среднем, а не всегда. На самом деле когда-то лучше может сработать CUPED, а когда-то — CUPAC или CUNOPAC. И как в каждом A/B-тесте выбрать, какой критерий сейчас лучше всего использовать?

Для ответа на этот вопрос был придуман критерий-Франкенштейн. Посмотрим на следующую схему:

Суть метода проста: берём N критериев и из них выбираем тот, который на текущий момент даёт наименьший доверительный интервал.

Какие критерии использовать внутри? У нас получилась следующая картина.

Для поюзерных тестов стоит использовать:

• CUNOPAC.

• CUMPED.

• CUPED.

CUPAC и Uplift-критерий не стоит использовать, так как они всегда работают хуже, чем CUNOPAC и CUMPED.

А для региональных тестов стоит использовать:

• Uplift-критерий.

• CUPAC.

• CUMPED.

• CUPED.

Почему критерий валиден?

Вопрос 1. Почему нет проблемы множественной проверки гипотез? Мы же провели на самом деле N тестов, и по-хорошему должны применить поправку Бонферрони/Холма. Ведь когда мы выбираем критерий с наиболее узким доверительным интервалом, мы можем как-то влиять на эффект.

Ответа два. Во-первых, проверено на 1000 А/А-тестах. Реальный уровень значимости (или ошибка первого рода) всегда был равен заданному теоретическому значению. Во-вторых, есть теоретическое объяснение. Если совсем просто, то мы смотрим не на p-value, а на ширину доверительного интервала, поэтому множественную проверку гипотез применять не надо. А теперь чуть более формально:

• Выборочное среднее и выборочная дисперсия независимы (в предположении, что CUPED-выборка из нормального распределения). Когда мы выбираем какой-то критерий, то мы выбираем его на самом деле по выборочной дисперсии. И в этот момент, если наша метрика была бы из нормального распределения, то можно было бы утверждать, что оценка эффекта никак не зависит от выборочной дисперсии. А значит, выбирая критерий по выборочной дисперсии, мы никак не влияем на оценённый эффект, то есть применять множественную проверку гипотез не надо. Можно считать, что на самом деле мы проверили результаты только одним критерием. Единственное «но»: всё это верно, если данные из нормального распределения, что на самом деле не так.

• В общем случае можно утверждать, что корреляция между выборочным средним и выборочной дисперсией стремится к 0 при увеличении размера выборки. Зависимость может и есть, но здесь играют роль три фактора: если даже она и есть, то нелинейная. Поэтому сложно придумать адекватную ситуацию на практике, когда при наиболее узком доверительном интервале будет наибольший/наименьший эффект. Хотя с точки зрения теории это вполне возможно. Далее, для нормальных случайных величин выборочное среднее и дисперсия независимы, отсюда есть шанс полагать, что и на ваших данных нет зависимости. Ну и в-третьих, у нас всё было проверено. Вы также можете проверить критерий у себя на данных и удостовериться, что всё хорошо.

Вопрос 2. Не заужаем ли мы доверительный интервал?

Для начала допустим, что на самом деле все критерии описывают одно и то же распределение, но полученное из разных семплирований. Например, пусть CUPAC и CUNOPAC строят ковариату из одного и того же распределения, просто она получилась разной в двух алгоритмах (получились разные выборки из одного распределения).

И вот здесь ответ неутешительный: да, мы можем заузить доверительный интервал. Представьте себе, что у нас N критериев, которые оперируют с нормальным распределением Norm(0, 1). Каждый из них как-то оценивает его дисперсию, и из всех этих оценок мы берём не любую, а наименьшую! Если среди этих N критериев хотя бы один критерий оценил дисперсию меньше, чем она есть на самом деле, то мы заузили доверительный интервал. При этом очевидно, что чем больше критериев, тем более вероятно, что хотя бы раз мы получим оценку дисперсии меньше реальной и ошибёмся. В качестве примера приведу код:

import scipy.stats as sps
import numpy as np
import matplotlib.pyplot as plt
 
small_number_of_criteria_std = []
large_number_of_criteria_std = []
 
# генерируем эксперимент 1000 раз, чтобы получить какое-то распределение для оценки дисперсии
for i in range(1000):
    # small_number_of_criteria, 5 критериев внутри критерия Франкенштейна
    current_std_array = []
    for i in range(5):
        # текущий критерий
        sample = sps.norm().rvs(100)
        # сохраняем std, полученное от критерия
        current_std_array.append(np.std(sample))
    # сохраняем текущее std, полученное от критерия Франкенштейна
    small_number_of_criteria_std.append(min(current_std_array))
     
    # large_number_of_criteria_std, 500 критериев внутри критерия Франкенштейна
    current_std_array = []
    for i in range(500):
        # текущий критерий
        sample = sps.norm().rvs(100)
        # сохраняем std, полученное от критерия
        current_std_array.append(np.std(sample))
    # сохраняем текущее std, полученное от критерия Франкенштейна
    large_number_of_criteria_std.append(min(current_std_array))
 
 
plt.hist(small_number_of_criteria_std, label='small number of criteria', bins='auto')
plt.hist(large_number_of_criteria_std, label='large number of criteria', bins='auto')
plt.xlabel('std')
plt.legend()
plt.show()

Мы видим, что чем больше критериев, тем сильнее дисперсия смещена в меньшую сторону. Так что если использовать очень много критериев, мы можем заузить доверительный интервал и создать некорректный критерий. 

Но на практике, во-первых, во всех критериях распределения всё же разные, во-вторых, у нас всего 3 или 4 критерия. При этом, на наших проверках, реальный уровень значимости каждый раз был заявленные alpha%. Мы проверили критерий на 1000 А/А- и A/B-тестах, как поюзерных, так и региональных, везде всё было корректно. Так что предложенный Frankenstein-критерий корректен. Но когда будете реализовывать его у себя, не забудьте дополнительно его проверить!

Результаты

Поюзерные тесты:

• Сокращение доверительного интервала на 14% относительно CUPED.

• С использованием парной стратификации: на 21%. 

Региональные тесты:

• Сокращение доверительного интервала в 1,5 раза относительно CUPED.

• С использованием парной стратификации: в 2 раза .

Получились отличные результаты! Особенно для региональных тестов.

Итого, в данной статье я постарался рассказать про такие методы, как:

• CUPED.

• CUPAC, CUNOPAC, CUNOPAC — три вариации на тему CUPED.

• Uplift-критерий — как из Uplift-модели сделать критерий.

• Frankenstein-критерий — как из нескольких критериев сделать один.

Если у вас остались вопросы, обязательно пишите. Постараюсь ответить.