Посвящаю моей любимой жене, инициировавшей домашнее чаепитие с просмотром видео.

Вместо предисловия

Идея оценить уровень справедливости при распределении ресурсов между людьми родилась в разговоре «на кухне» при просмотре видео о росте количества инфо-мошенников (в оригинале «инфо-цыган», которые «лечат» неуспех с помощью «правильной» постановки целей и «личностного роста» ). В продолжении данной тематики был приведен интересный факт из компетентного источника: «эзотерика занимает на рынке обучающих электронных курсов твердое второе место» (!). Этот факт показался мне вполне естественным ввиду того, что не всегда большое количество усилий, приложенных человеком в направлении достижения цели, приводит к ожидаемому результату. Как следствие – «ищем причины в себе». Для иллюстрации закономерности данного факта родилась модель «крошек» (на столе, за которым мы сидели после обеда) – модель справедливого распределения ресурсов, при которой тем не менее появляются «обделенные» и «обездоленные».

Описание модели

Суть модели проста: на столе равномерно разбросаны крошки, которые очень любят микробы, ползающие по столу (вместо микробов можно представить мини-муравьев, или других мелких существ, которые умеют ползать в поисках еды). Далее будем их называть точками. Точки олицетворяют людей, а крошки – материальные ресурсы, к которым люди стремятся.

Будем предполагать, что точки распределены по столу равномерно, равно как и крошки. Любое отклонение от равномерного распределения будет порождать несправедливость: преимущество в возможностях доступа к крошкам одних точек над другими. (Мы же хотим создать «справедливые» условия для всех.)

Каждая точка видит свою ближайшую крошку и движется к ней. Будем предполагать, что скорость движения точек к своим крошкам одинаковая у всех (опять-таки из соображений справедливости).

И наконец, сделаем так, чтобы между точками не было «конкуренции» («стратегия голубого океана»), пусть для каждой точки найдется своя крошка, достигнув которой она будет «счастлива». И если две точки достигают одной крошки (в разное время), то «счастье» достается обеим.

Казалось бы, мы создали мир равных возможностей. Посмотрим, так ли это на самом деле…

Исследование модели

Для начала упростим модель и перейдем от двумерности на плоскости к одномерному представлению:

Ввиду того, что распределение по каждой из осей является независимым и равномерным, упростим модель, рассмотрев одномерный случай, когда точки движутся к крошкам на прямой.

Распределение точек на прямой – равномерное, распределение крошек – равномерное также.

Моделирование произведем средствами Excel. Рассмотрим, например, 100 точек и 100 крошек на единичном отрезке (от 0 до 1). Разбросаем точки и крошки с помощью датчика псевдо-случайных чисел (в Экселе используется генерация по алгоритму «Вихрь Мерсена»). Посчитаем расстояния от каждой точки до каждой крошки. Расстояние будем рассчитывать как модуль разности между координатами точки и крошки на прямой Х.

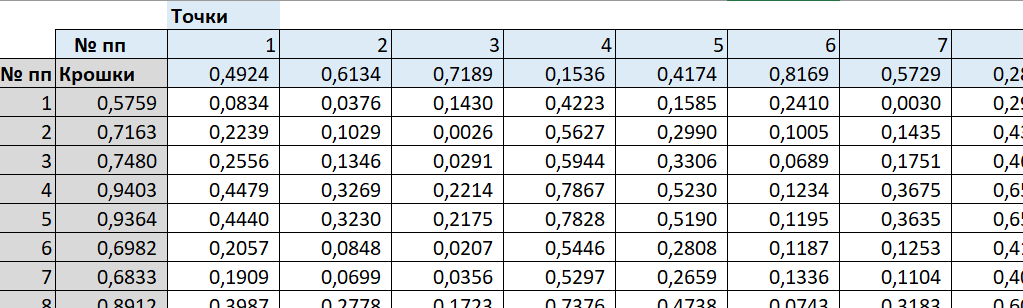
Ввиду того, что точка движется к ближайшей крошке, упорядочим расстояния от каждой точки до крошек по возрастанию. Посмотрим, как выглядят графики распределения расстояний до крошек по каждой выбранной точке:

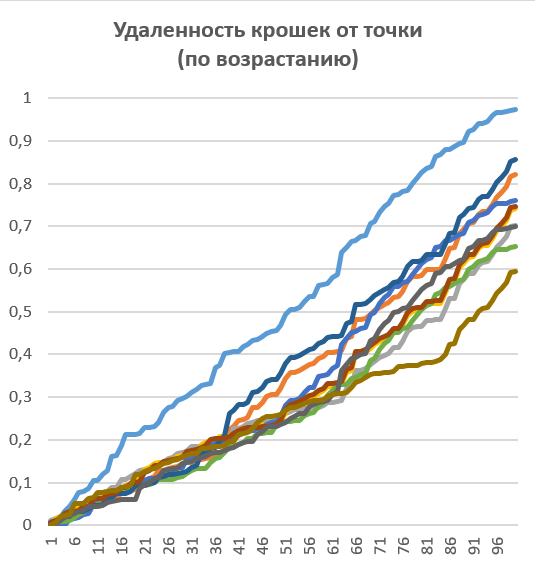
На рисунке представлены графики удаленности крошек для десяти случайно выбранных точек.

Как нетрудно видеть, графики близки к линейным, что подтверждает равномерность функции распределения случайной величины, примененной при моделировании.

Примечание: В идеале мы должны получить семейство прямых, которые начинаются в нуле, а заканчиваются в точке на интервале от 0.5 до 1. Угол наклона прямой зависит от расположения точки на интервале (0;1). Для точек, расположенных ближе к центру отрезка (0;1), максимальное расстояние до крошки стремится к 0.5 (сверху), т.к. расстояние от центра до краев равно 0.5).

Теперь выберем для каждой точки лишь одну «целевую» крошку, расстояние до которой минимальное. Получим вектор расстояний до ближайших крошек, которые нужно преодолеть каждой точке для достижения цели.

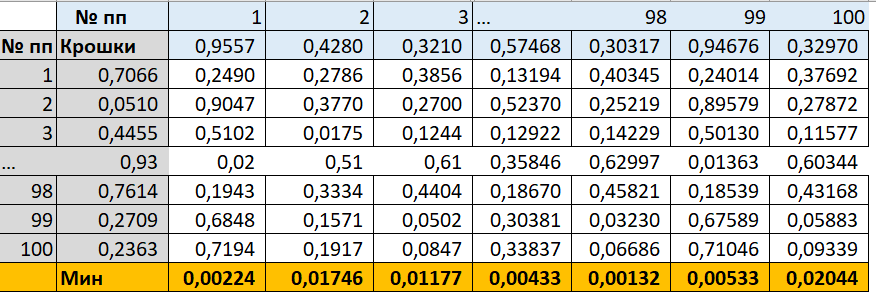
Упорядочим минимальные расстояния до крошек по возрастанию (по аналогии с тем, что мы делали выше). Получим график распределения расстояний до ближайшей крошки по точкам.

Повторим данную операцию для нескольких выборок точек и крошек.

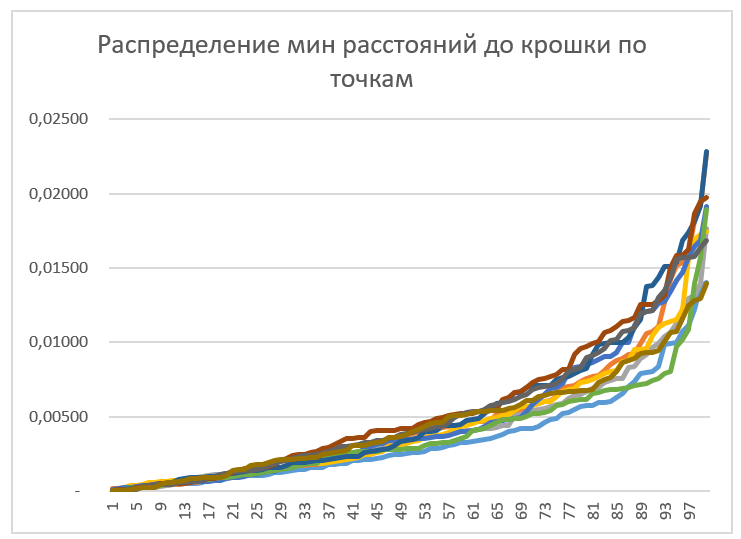
Усредним полученный результат. В нашем случае достаточно было 10 выборок минимальных расстояний, т.к. их среднее сходится к одному графику:

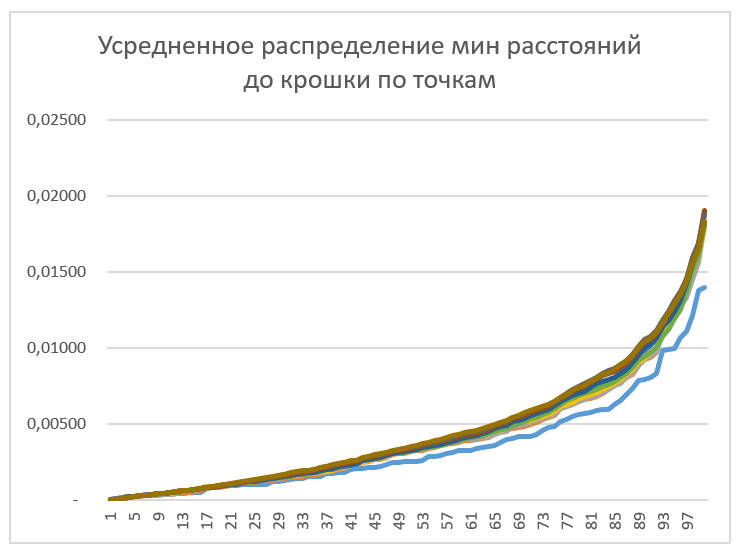
Усреднение последовательно производилось по 1,2,3…10 выборкам.

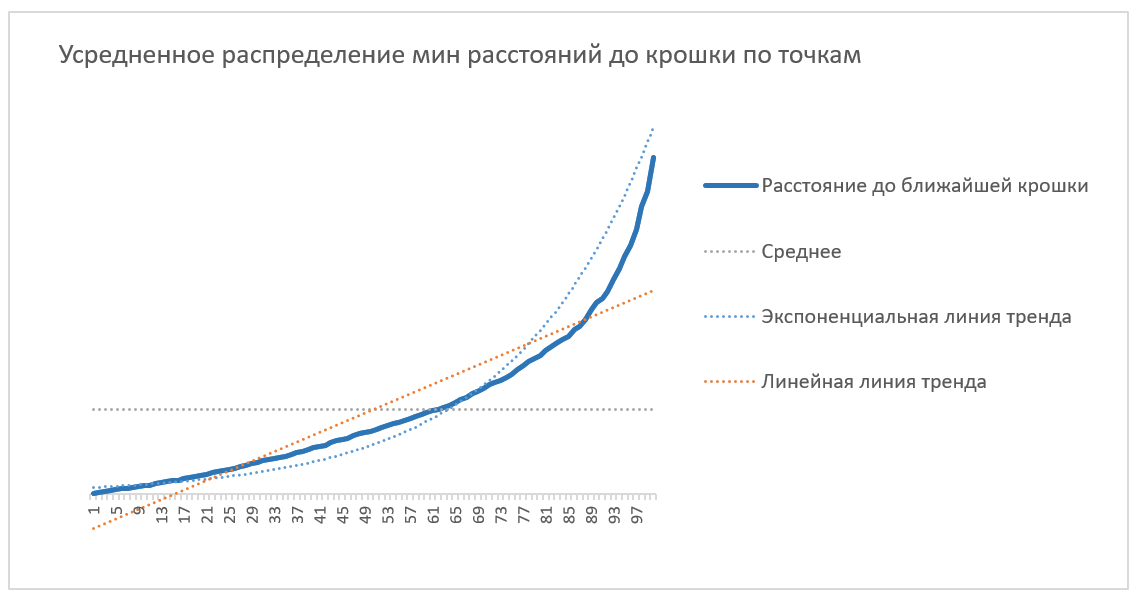
 Полученный график среднего распределения расстояний от точек до крошек не является линейным. Первая его половина больше похожа на линейную функцию, но вторая – на экспоненциальную.

Уже сейчас можно видеть, что есть точки, у которых расстояние до ближайшей крошки существенно превышает среднее. Но для того, чтобы делать выводы, представим данную кривую в несколько ином виде: на оси Х отложим отрезок расстояний до крошек от минимального до максимального, а по оси Y будем отмечать количество точек, для которых расстояние до крошки меньше заданного. Получим такой график:

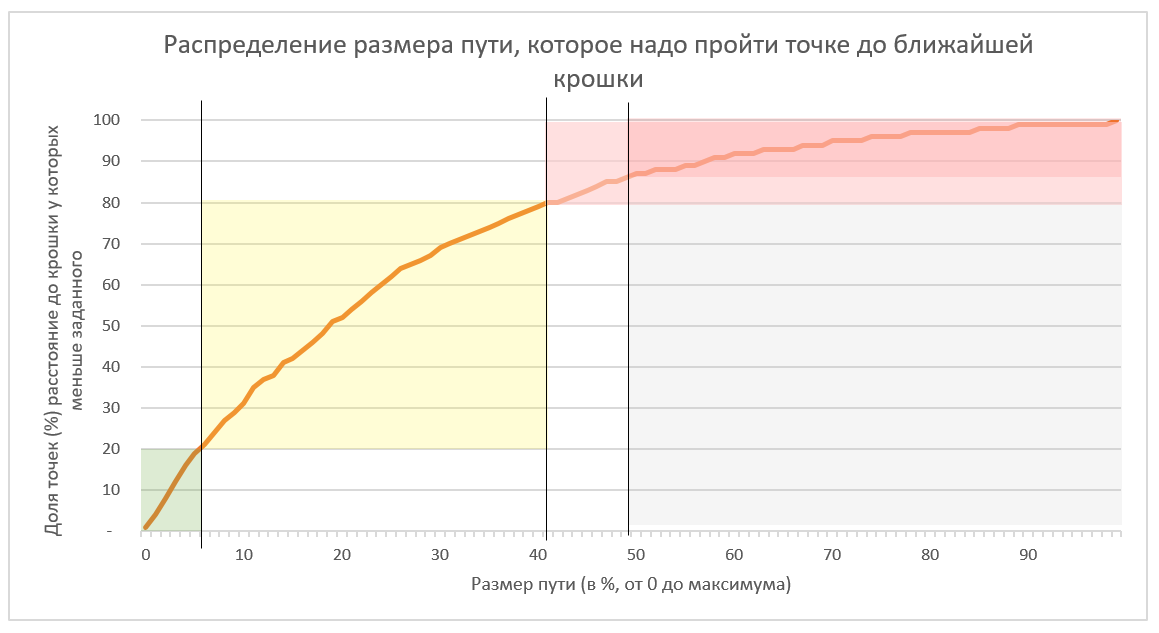
Читается данный график так:

• Зеленая область: Для 20% точек расстояние, которое надо преодолеть до крошки, не превышает 6% от максимально возможного (это «счастливцы»)

• Желтая область: для 60% точек в диапазоне от 20 до 80%) расстояние до крошки не превышает 40% от максимального («середнякам» нужно приложить не более 40% от возможных усилий, чтобы достичь цели)

• Ярко красная область: Для порядка 15% точек расстояние, которое надо преодолеть, более чем в 2 раза превышает то, которое преодолевают 80% точек для достижения цели (это «несчастные точки»).

Выводы

Удивительным образом, несмотря на то, что распределение точек и крошек было выбрано равномерным, путь движения к цели для разных точек оказался существенно различным. А именно:

Существует 20% «счастливцев», для которых путь до цели составляет порядка 15% (6/40) от пути среднестатистического индивидуума. Объем ресурсов (в т.ч. требования к личностным качествам) для достижения цели для этой категории граждан существенно ниже, чем для большинства, «в силу их рождения».  Однако количество людей, находящихся «неподалеку» от «счастья» достаточно велико для того, чтобы между ними могла возникнуть конкуренция. Но она не исключает случая, когда «дуракам везет».

С другой стороны, существует порядка 20% «несчастных», для которых путь движения к цели более чем в 2 раза (!) превышает путь 80% остальных. Что это значит на практике?

Движение обычно связано с затратами ресурсов. Это могут быть: время, деньги, энтузиазм, лояльность и пр. Есть люди, которые вложили в движение все, и даже в разы больше того, что вкладывают другие, и при этом не достигли результата. Могут ли они винить себя? Нет. Просто им не повезло с начальной точкой. Но они этого не знают…

В условиях «невезения», когда окружающую среду не удается изменить, а у других вокруг – успех при меньших вложениях, возникает ощущение бессилия, и единственный вывод, который можно сделать в этих условиях, только один – «что-то не так во мне». Именно поэтому у курсов с названием «Марафон желаний» или практик связанных с «личностным ростом» всегда будет свой клиент.

А Бога винить не нужно, он сделал все, что мог J .

PS: Интересное (и короткое) видео про обоснование собственного успеха у «голубей Скиннера» можно посмотреть в этом видео.