О пакете BinSeqBstrap
Постановка задачи
Допустим, у нас есть какая кусочно-гладкая функция f(x), к который прибавлен некий случайный шум, соответствующий условиям Гаусса-Маркова. И все хорошо, только эта самая функция f(x) – функция с неустранимым(-и) разрывом(-ами) первого рода, то есть в какой-то точке левый и правый предел этой функции равны разным числам, а у функции есть скачок. Задача – как-то нужно научить алгоритм распознавать этот скачок.
Минутка теории
Теоретические основы изложены в виньетке, написанной Кэти МакДэйд и Флориана Пэйна из Кэмбриджа, опубликованной вот тут.
Если вкратце, то функционал пакета позволяет решить 4 разные подзадачи, базовая из которых - определение места и размера единственного скачка функции при известной ширине окна h
Основа: вот эта вот длинная формула

Результат этой формулы используется для вычисления места скачка
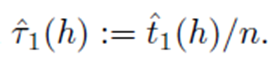
Сам метод основан на идеях непараметрической регрессии. Для определения местоположения точек разрыва выбирается окно из некоторого количества точек, и считается разница между суммами значений слева и справа. Для определения размера скачка используется разница значений сглаженной функции в определенной точек разрыва.
Практика
В коде это выглядит так:
library(BinSegBstrap)
## Часть 1
set.seed(1)
n <- 1:100
signal <- 0.1*n-5
signal[51:100] <- signal[51:100] + 5
y <- rnorm(n) + signal # Придумываем искусственные данные
est <- estimateSingleCp(y = y, bandwidth = 0.1)
est$cp # определяем точку разрыва
est$size # определяем скачок функции
plot(y, pch = 16, col = "grey30")
lines(signal)
lines(est$est, col = "red") # est$est - подогнанные значения

Часть 2. Определение параметров скачка при неизвестной величине
Собственно, к исходной формуле достраивается только алгоритм кросс-валидации, который позволяет найти лучший размер окна, в котором искать скачок.
Зададим алгоритму задачку посложнее:
set.seed(1)
n <- 1:100
signal1 <- 5-0.1*n
signal2 <- 0.01*n^2-20
signal<-c(signal1[1:50],signal2[51:100])
y <- rnorm(n) + signal
est <- estimateSingleCp(y = y)
est$bandwidth # подобранная ширина окна
est$cp # определяем точку разрыва
est$size # определяем скачок функции
plot(y, pch = 16, col = "grey30") # plot of observations, true and estimated signal
lines(signal)
lines(est$est, col = "red")
Часть 3. Проверка статистической гипотезы о наличии скачка
Объявляем нулевую гипотезу о том, что размер скачка К равен 0 (альтернативная – не равен).
Дальше с помощью бутстрэпа получаем множество оценок величины этого скачка (много-много раз решаем чуть разные задачи из п.2) и смотрим, выполняется гипотеза или нет.
В коде это выглядит так:
test <- BstrapTest(y = y)
test$outcome # Результат проверки гипотезы о нулевом скачке
test$pValue
Часть 4. Поиск всех возможных точек разрыва
Составим функцию, в которой есть две точки разрыва, и посмотрим, справится ли алгоритм с ней
set.seed(1)
signal1<-abs(-8-seq(from=-10, to=-5, length.out=50))
signal2<-3*exp(seq(from=-5, to=0, length.out=50))
signal3<-sqrt(seq(from=0, to=10, length.out=50))-4
signal <- c(signal1,signal2,signal3)
y <- rnorm(150) + signal
est <- BinSegBstrap(y = y)
est$cps # находим точки разрыва
plot(y, pch = 16, col = "grey30") # plot of observations, true and estimated signal
lines(signal)
lines(est$est, col = "red")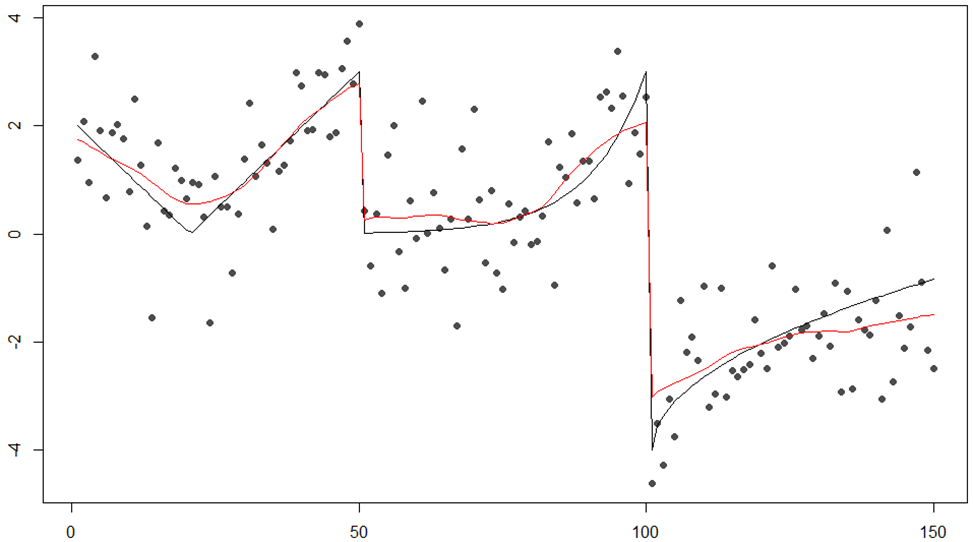
Вместо заключения
Весьма интересная задумка. Для решения практических задач в текущем состоянии пакет применим мало, к тому же редко приходится данные аппроксимировать функциями с разрывами, но как инструмент вспомогательного анализа может пригодиться. Ну и интересно потестить, до каких пределов алгоритм работает хорошо, а когда начнет пропускать разрывы / находить лишние.
Комментарии (4)

adeshere
19.02.2022 22:02+5Спасибо за публикацию. Не думал, что об этом до сих пор пишут статьи в математические журналы;-)
При анализе геодеформационных процессов разрывы в рядах возникают сплошь и рядом. Например, для наклономеров типичен дрейф нуля. Периодически ряд выходит на границу динамического диапазона, и экспериментатору приходится руками "подкручивать" ноль, чтобы вернуть сигнал в центр диапазона. На графике получается скачок уровня. Для тех, кто ведет подобные наблюдения, устранение таких скачков - это повседневная бытовая задача ;-)
Только в отличие от рассмотренной модели, на практике все немного сложнее. Во-первых, разрыв или скачок - это часто не одна точка, а некоторый переходный процесс с заранее неизвестной длительностью (хотя может быть и одна точка). Во-вторых, скачок очень часто сопровождается более или менее длительным перерывом в наблюдениях. В-третьих, после скачка в сигнале часто присутствует переходный процесс, связанный с эффектом экспериментатора (приборы довольно чувствительные и каждое посещение штольни - это стресс для прибора и катастрофа в сигнале).
Еще надо учитывать, что в период "послескачкового" пропуска наблюдений нормальный ход деформаций идет себе дальше. Поэтому нельзя просто выровнять уровень ряда на правом и левом концах перерыва. Надо как-то убрать скачок, но не исказить при этом нормальный процесс.
А еще бывают скачки непонятной природы. Он может быть как реальным эффектом в геосреде, так и локальным артефактом в постамента (треснула микропесчинка под опорой прибора). Но их тоже надо убирать чтобы, к примеру, взяться за анализ приливов.
Я вот тоже недавно получил такой ряд и задачу - подготовить его для последующей обработки. А я эту тему раньше совсем не курил, и литературу не знаю. Поэтому собрал алгоритм для устранения скачков из того, что было по рукой (в нашем пакете). Получилось примерно вот так:
1) очищаем сигнал (который с разрывами и скачками) от всех неслучайных составляющих которые можно там выделить (прилив, долговременные тренды и др.)
2) делаем медианное сглаживание в скользящем окне для подавления шума. Окно лучше взять из нечетного числа точек, чтобы сохранить амплитуду скачка, если он вдруг происходит одномоментно;
3) ряд до и после скачка аппроксимируется линейной функцией; эти функции экстраполируются навстречу друг другу;
4) вычисляется разность линейных функций на том временном интервале, который включает: а) сам скачок, плюс б) перерыв в наблюдениях после скачка, плюс в) переходный процесс после скачка. Поскольку две экстраполированные линейные функции не вполне параллельны, разность - это тоже линейная функция, у которой есть среднее значение (= амплитуда скачка) и дисперсия/сигма (= погрешность его оценки). Погрешность нужна для того, чтобы оценить искажения долговременных вариаций, которые мы вносим в сигнал, убирая скачки.5) Ну и конечно, скачок после этого убирается из исходного ряда (то есть того, который с приливом и трендами), а не из очищенного суррогата, по которому все оценивалось ;-)
Картинки
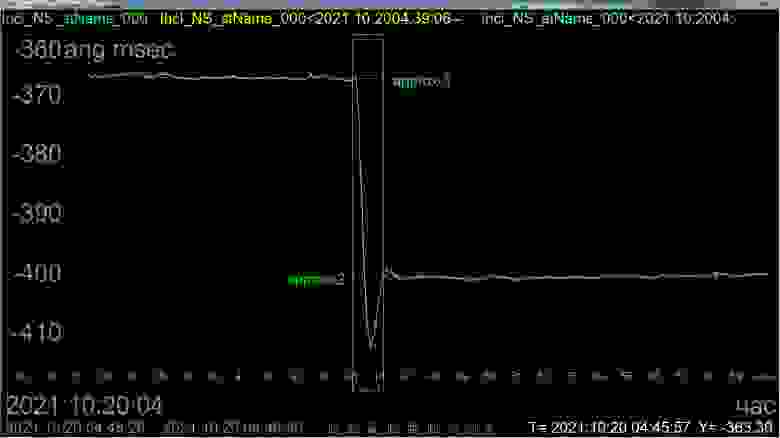
Это идея метода 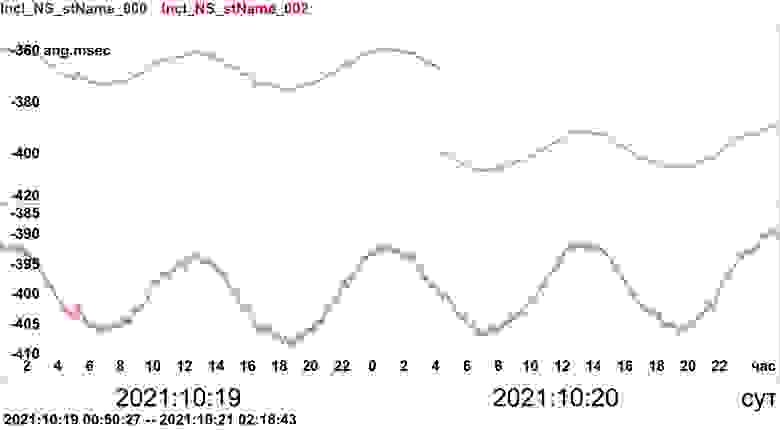
А это результат 
И он же в крупном масштабе Но поскольку все эти трюки - это сугубо техническая задача, то у нас (в статьях по анализу данных режимных наблюдений) как-то даже не принято об этом писать. Считается, что обсуждать такую тривиальщину незачем. А я вдобавок в данной тематике новичок, поэтому тем более странно с таким велосипедом публиковаться: настоящие спецы засмеют. Хотя алгоритм в общем рабочий, и с задачей справляется. Но ведь люди на этих скачках десятилетиями собачек едят, а я за пару дней на коленке сварганил...
А тут оказывается в Кембридже вон оно как - про скользящее среднее пишут. Неожиданно, да.
P.S. Код процедуры не привожу, так как он состоит из целой кучи небольших почти тривиальных функций, раскиданных по разным местам пакета, и ужасающего legacy, необходимого, чтобы юзер мог заставить все эти функции работать вместе в нужном порядке, просто нажимая на кнопочки в интерфейсе (без программирования). Вдобавок сам алгоритм не автоматический: многие настройки (особенно величину всяких оценивающих окон) юзер задает или проверяет интерактивно на графике.
P.P.S. А впрочем, для любителей ужасов вот ссылка на исходники пакета в целом ;-)

acheremuhin Автор
20.02.2022 15:16Формально, задачи все-таки разные. Вы, как я понял, говорите про временные ряды. Для них задачи определения скачка, точек излома тренда и т.д. решаются по-другому. Тут все-таки рассматривается не временной ряд, плюс у вас своя практическая специфика. Нельзя знать совсем все методы и приемы во всех областях знания. Поэтому - не бейте пианиста, он играет как умеет.





iggr63
Где взять этот пакет?
acheremuhin Автор
Он в открытом доступе. Он скачивается и устанавливается в R обычным путем