Классический критерий Манна-Уитни позволяет проверить нулевую гипотезу о равенстве распределений в двух выборках. Простота общей идеи (взять две выборки, смешать их в одну и работать с рангами значений, относящихся к первой и второй выборке) позволяет задуматься над тем, как обобщить ее на случай, если выборок больше двух.

Собственно, именно про это и рассказывается в статье Fisher, D., Oja, H. Mann-Whitney Type Tests for Microarray Experiments: The R Package gMWT / Journal of Statistical Software. 2015. Volume 65, Issue 9.

Минутка теории

Возьмем несколько выборок, и проверим гипотезу о равенстве их распределений.

Для классического случая двух выборок получим, что значение статкритерия равно математическому ожиданию величины

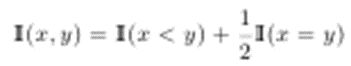
Соответственно, проверка нулевой гипотезы – это проверка гипотезы о равенстве матожидания ½ (если одно из распределений будет смещено существенно правее, то матожидание устремится к 0 или 1)

Куда интереснее все для случая, например, трех выборок.

Там уже необходимо искать матожидание выражения

Тогда нулевая гипотеза о равенстве всех этих распределение эквивалентна проверке гипотезы о равенстве статкритерия 1/6.

С альтернативными же гипотезами несколько сложнее. Авторы выделили следующие виды альтернативных гипотез:

- первый тип альтернативных гипотез – распределение какой-то пары переменные неодинаково;

- второй тип альтернативных гипотез – в одной из какой-то пары переменных распределение одной из них смещено вправо;

- третий тип альтернативных гипотез: распределение двух переменных смещено вправо относительно третьей;

- четвертый тип гипотезы: распределения всех трех переменных последовательно смещены вправо относительно друг друга

Практика

Теперь попробуем что-то посчитать. Для этого в пакете есть две основные функции – estPI и gmw

Функция estPI вычисляет непосредственно математическое ожидание приведенных выше функций (фактически, величину статкритерия), gmw – непосредственно проводит статистический тест.

Возьмем датафрейм CASchools, и проверим гипотезу о равенстве распределений величины количества студентов, которых оценивают по разным системам оценок:

library(AER)
library(dplyr)
library(gMWT)
data("CASchools")
data <- as.matrix(CASchools[,c(4,5)] %>% arrange(desc(grades)))
gmw(data[,2], data[,1],test="kw",type="external")

Р-значение: 0.5823868, что больше традиционного критического значения в 0.05, значит, мы не можем отвергнуть нулевую гипотезу о равенстве распределений. График плотности распределений, в принципе, говорит нам нечто похожее:

Посмотрим на то, как это работает в случае трех выборок. Возьмем датафрейм PSID1776 и проверим гипотезу о равенстве распределений количества часов работы для работников с разным количеством молодых детей (от 0 до 2, тех, у кого 3 ребенка, из выборки убираем)

data("PSID1976")
glimpse(PSID1976)
table(PSID1976$youngkids)
data <- as.matrix(PSID1976[PSID1976$youngkids < 3,c(2,3)] %>% arrange(desc(youngkids)))
gmw(X=data[,1], g=data[,2],test="triple")

Для данной альтернативной гипотезы р-значение равно 1, нулевую гипотезу отвергать нельзя. График распределения показывает что-то похожее

Ну а для быстрой проверки других альтернативных гипотез можно использовать функцию estPI

res_2 <- estPI(data[,1], data[,2], type="pair", goi=NULL, mc=1, order=TRUE, alg="Cnaive")
res_2
res_2 <- estPI(data[,1], data[,2], type="triple", goi=NULL, mc=1, order=TRUE, alg="Cnaive")
res_2

В данном случае обозначения групп связаны с количеством детей: группа 1 – работники, у которых нет детей; группа 2 – работники, у которых 1 ребенок, группа 3 – работники, у которых 2 ребенка.

По графику функций распределения – чем больше детей, тем левее смещено распределение.

Об этом свидетельствует значения критериев – все они меньше 0.5, что говорит о невыполнимости условия x<y – чаще встречается x>y

Дополнительно

Дополнительно функционал данного пакета может применяться для проверки гипотез о соответствии распределения некоторому закону.

Возьмем пакет LNPar, где рассматривается распределение, состоящее из смеси логнормального и распределения Парето; однако в пакете не рассматривается функционал проверки гипотез.

Берем данные датафрейма CASchools и построим график распределения величины дохода школьников

library(LNPar)
ggplot(CASchools, aes(x = income)) +
  geom_density(alpha = 0.2) 

# Подгоним под данные значения функции распределения
LPfit(CASchools$income,90,0)
# Вытащим исходные значения и создадим данные по распределению:
income <- (CASchools$income)
income_Sim <- (rLnormParMix(420,pi=.9574806,mu=2.598694,sigma=0.3307882,xmin=33.455,alpha=5.753251))
# Проверим гипотезу о равенстве распределений 
data_3 <- as.data.frame(cbind(income,income_Sim))
gmw(data_3[,2], data_3[,1],test="kw",type="external")

По результатам теста – нельзя отвергнуть гипотезу о равенстве распределений. Посмотрим на график:

Графики плотности распределений исходных и симулированных данных похожи – значит, можно сказать, что распределение значений доходов школьников подчиняется смеси логнормального и Парето-распределений.