Классические статистические тесты – это, как правило, тесты, проверяющие гипотезу о равенстве (медианы определенному значению, средних в двух независимых группах, дисперсии во многих зависимых группах, коэффициента корреляции нулю и т.д.).

Однако уже более как 30 лет существует альтернативный подход, разработанный в ходе исследований по психологии – тесты эквивалентности. Он основан на идее, например,  что некоторое  отличающееся от нуля значение корреляции все равно может считаться незначимым для конкретной решаемой задачи.

В R за реализацию тестов подобного типа отвечает пакет negligible. Рассмотрим поэтапно разные практические задачи, добавим к каждой щепотку теории и расчетов.

1) Тесты корреляции на основе эквивалентности (для нормально распределенных величин)

Подробное объяснение в статье: Goertzen,  J.  R.,  &  Cribbie,  R.  A.  (2010).   Detecting  a  lack  of  association.   British  Journal  of  Mathematical  and  Statistical  Psychology,  63(3), 527–537

Вкратце: мы проверяем сразу две нулевые гипотезы в виде –r* < r и r > r*, где r* - установленная нами граница незначимости коэффициента корреляции, r – коэффициент корреляции по нашим данным.

Практика: возьмем базу данных CASchools и проверим гипотезу о том, что коэффициент корреляции между результатами тестов по математике и чтению находится в диапазоне незначимости [-0,2 ; 0.2]

library(AER)
library(negligible)
library(tidyverse)
data(CASchools)
CASchools <- as.data.frame(CASchools)
neg.cor(v1 = CASchools$math, v2 = CASchools$read, eiU = .2, eiL = -.2)

Границы диапазона незначимости устанавливаются пользователем, исходя из задачи, и могут быть различны. Алгоритм выводит:

- величину коэффициента корреляции: 0.9229;

- 95%-ый доверительный интервал для него, посчитанный на основе бустрэпа;

- вывод по нулевой гипотезе (в нашем случае гипотеза о незначимости коэффициента корреляции отвергается).

2) Тест эквивалентности пропорций (тест 2 на 2)

Практика: возьмем базу данных CASchools и проверим гипотезу об эквивалентности пропорций в таблице для двух переменных – применяемой системе оценок (КК-06 или КК-08) и превышении медианного значения баллов по математике

v1<-as.vector(CASchools$math>median(CASchools$math))
v2<-as.vector(CASchools$grades)
tab<-table(v1,v2)
tab
neg.cat(tab=tab,alpha=.05,eiU=0.5,nbootpd=50)

Алгоритм выводит:

- значение классического критерия Крамера и его 95%-ый доверительный интервал;

- сравнение верхнего значения коэффициента Крамера и заданного пользователем значения незначимости;

- вывод по нулевой гипотезе (в нашем случае гипотеза о незначимости разницы в пропорциях принимается).

3) Тест на наличие влияния третьей переменной на корреляцию между двумя другими.

Подробнее в статье на http://doi.org/10.20982/tqmp.16.4.p424

Вкратце: строятся две модели связи между переменными:

Необходимо понять, существует ли связь между X и Y, или она вся объясняется тем, что обе эти переменные коррелируют с какой-то другой переменной М.

Практика: возьмем базу данных CASchools и проверим гипотезу о том, что коэффициент корреляции между результатами тестов по математике и чтению объясняется количеством компьютеров.

neg.esm(X = math,Y = read,M = computer,eil = -.15,eiu = .15,
        nboot =  50,data = CASchools)

Итоговый вывод по двум примененным процедурам: нулевая гипотеза о том, что прямое влияние переменных (разница между общим и косвенным эффектом) не пренебрежимо мало, не может быть отвергнута. То есть, величина прямого влияния переменных не входит в заданный по умолчанию интервал [-0.15 ; 0.15].

4) Тест эквивалентности дисперсий в независимых выборках.

Подробнее в статье на https://doi.org/10.1080/00220973.2017.1301356

Практика: возьмем базу данных CASchools и проверим гипотезу о том, что дисперсия оценок по математике среди студентов, оцениваемых по-разному, различается незначительно

neg.indvars(dv = CASchools$math, iv = CASchools$grades, eps = 0.25)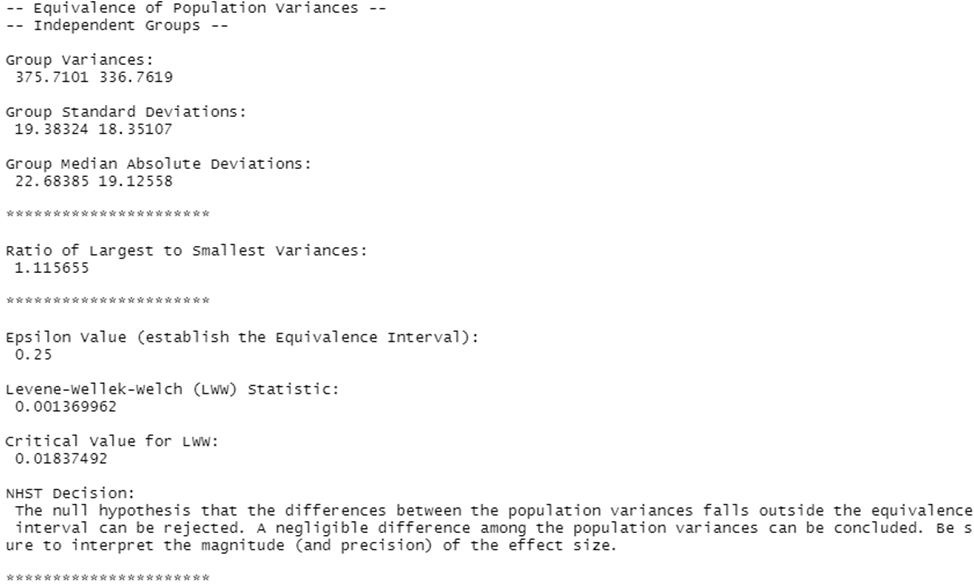

Итоговый вывод включает:

- величины групповой дисперсии, стандартного отклонения и абсолютного медианного отклонения

- рассчитанное значение отношения дисперсий

- тестовую статистику и выводы по ней (в нашем случае гипотеза о том, что величина различия между дисперсиями населения выходит за пределы интервала эквивалентности, может быть отвергнута).

Существенной сложностью широкого применения данного теста является оторванность от конкретных значений конкретного показателя величины eps, определяющей «жесткость» теста. Есть только рекомендация в одной статье использовать значение 0.25, если хотите провести консервативный тест, и значение 0.5 – если либеральный.

5) Тест на незначимость разницы средних значений в зависимых группах

Практика: возьмем датафрейм PSID7682 и проверим гипотезу о эквивалентности заработной платы в 1976 и 1982 годах

data("PSID7682")
date <- rbind(PSID7682[PSID7682$year==1976,c(13,12,14)],PSID7682[PSID7682$year==1982,c(13,12,14)])
neg.paired(outcome = date$wage, group = date$year, ID = date$id,eil=-10,eiu=10)

Итоговый вывод очень подробный – выводятся средние, дисперсии, среднеквадратичное отклонение, абсолютное медианное отклонение по группам. По сути проверяемой гипотезы можно сказать следующее: нулевая гипотеза о том, что разница между средними превышает интервал эквивалентности (который задается параметрами eil и eiu), не может быть отвергнута.

6) Тест эквивалентности на незначимости влияния предиктора в модели регрессии

Практика: построим по датафрейму CASchools модель зависимости баллов по математике от количества учителей, компьютеров и среднего дохода, проверим значимость предиктора «количество учителей»

neg.reg(formula=math~teachers+computer+income,data=CASchools,predictor=teachers,eil=-.1,eiu=.1,nboot=50)

Итоговый вывод показывает значение коэффициента при переменой, его 95%-ый доверительный интервал. Общий вывод: нулевая гипотеза о том, что коэффициент регрессии не является незначительным, может быть отклонена.

7) Тест об эквивалентности двух коэффициентов корреляции в группах

Практика: проверим по датафрейму CASchools гипотезу о эквивалентности корреляций между баллами по чтению и математике для студентов с разными системами оценок

yx1 <- CASchools %>% filter(grades=="KK-06")
yx2 <- CASchools %>% filter(grades!="KK-06")
neg.twocors(r1=cor(yx1$math,yx1$read),n1=length(yx1$math),r2=cor(yx2$math,yx2$read),n2=length(yx1$math),eiu=.15,eil=-0.15,  dep=FALSE)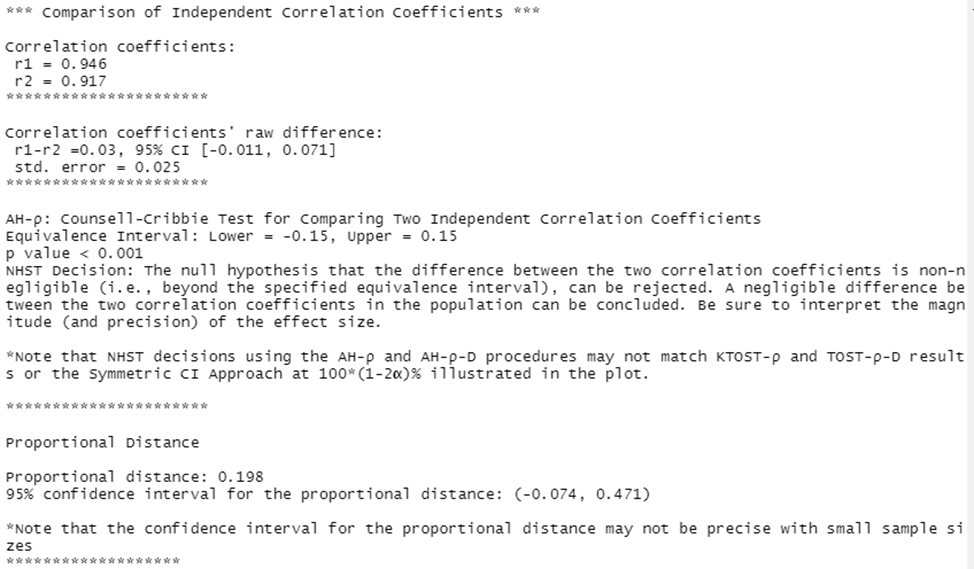

Итоговый вывод показывает значение коэффициентов корреляции, 95%-ый доверительный интервал величины разницы между ними, и позволяет сделать вывод о том, что нулевая гипотеза о незначительности разницы между двумя коэффициентами корреляции может быть отклонена.

8) Тест на незначимость разницы средних значений в независимых группах

Практика: возьмем датафрейм CASchools и проверим гипотезу о эквивалентности средних значений баллов по математику для школьников, оценивавшихся по разным системам оценки

neg.twoindmeans(dv=math,iv=grades,eiL=-1,eiU=1,data=CASchools)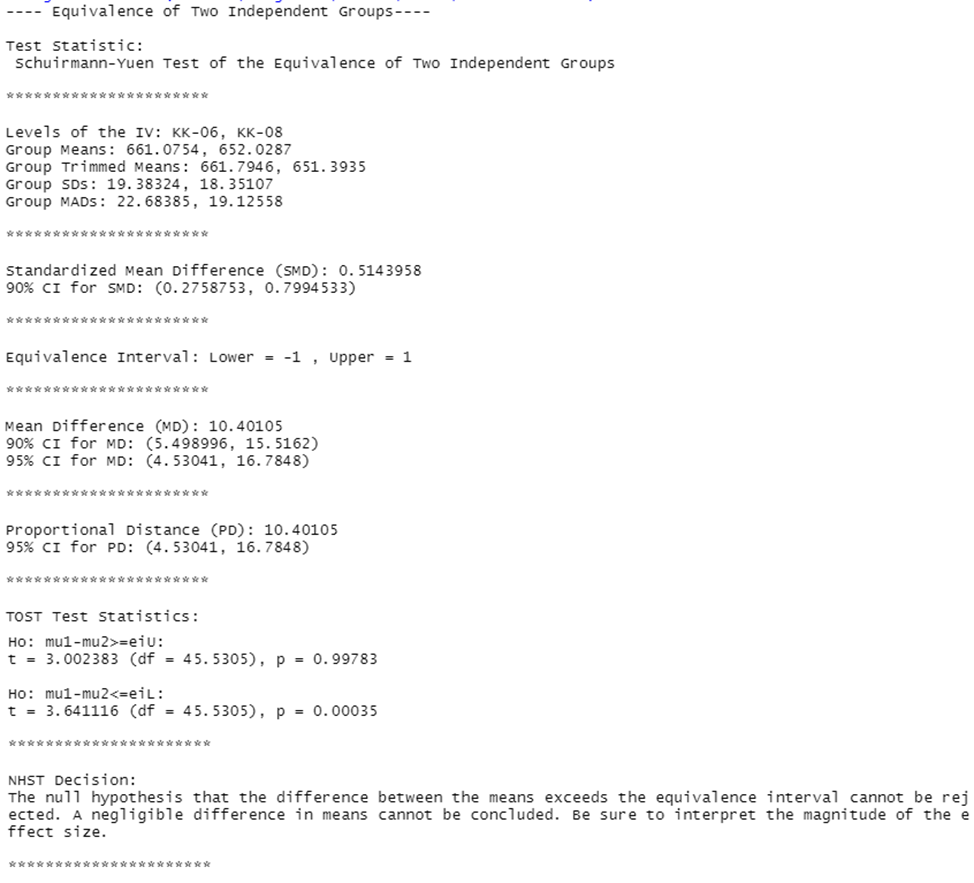

Итоговый вывод показывает значения групповых средних, стандартизированную величину разницы средних и ее 90%-ый доверительный интервал, а также результаты проверки двух статгипотез о том, что разница средних больше по модулю заданных экстремальных значений, по согласно которым нельзя отвергнуть нулевую гипотезу о том, что разница между средними превышает интервал эквивалентности.