В идеальном мире реализация статистического теста должна быть понятной, красивой и быстрой. До идеала, нам, конечно, далеко, но иногда попадаются достойные попытки к нему прийти.

Сегодня речь пойдет о пакете chisquare, который реализует классические статистические тесты на равенство пропорций — причем не только для таблиц 2*2, но и для таблиц 2*k.

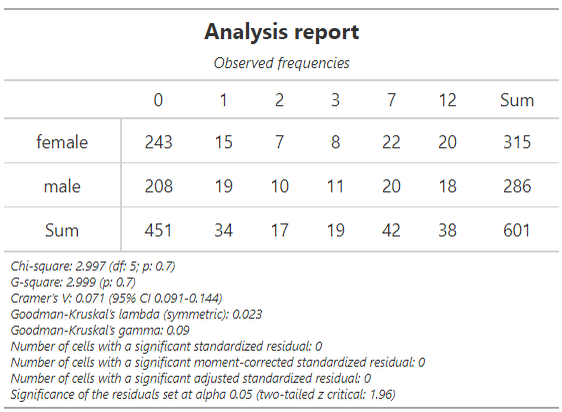
Возьмем датафрейм Affairs о супружеских изменах и построим по нему таблицу, которая отражает информацию о встречаемости у людей разных сочетаний значений переменных «пол» и «частота измен». И потом проверим гипотезу о равенстве пропорций:

library(AER)
library(dplyr)
library(chisquare)
data("Affairs")
glimpse(Affairs)
data <- unclass(table(Affairs$gender,Affairs$affairs))
res <- chisquare(data, plot.or=FALSE, reference.level=1, row.level=1)

Вся числовая статистика сохранена в переменной res; ну а существенным бонусом является то, что попутно пользователю будет выведено 7 графиков. Самыми полезными, на мой взгляд, являются первый и последний. В последнем, собственно, будет представлена обобщенная информация о результатах проверки гипотез:

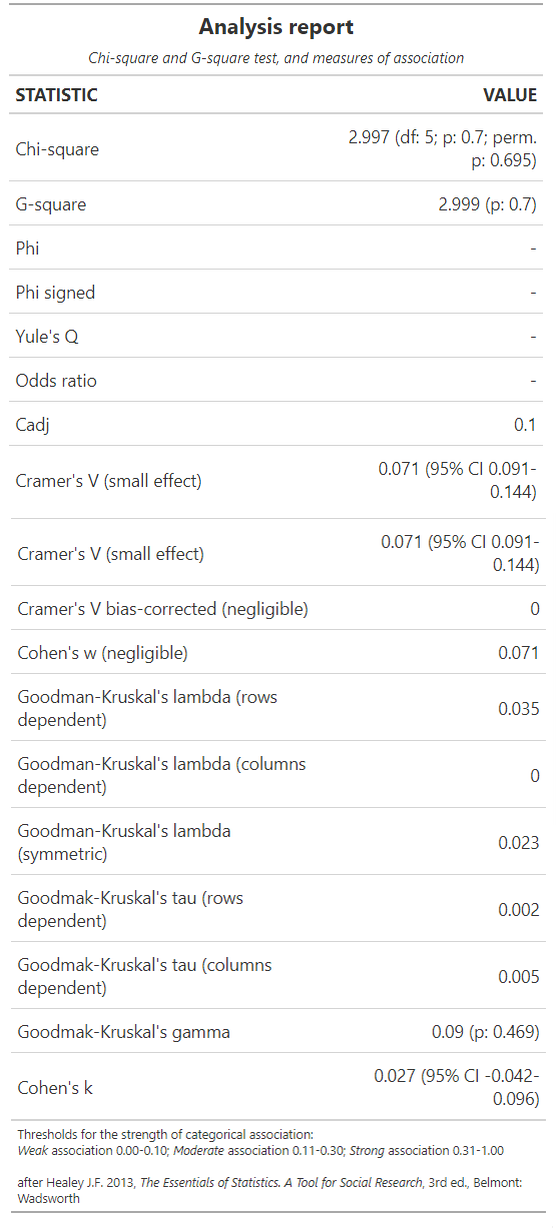
Первые два значения, собственно, показывают нам результаты проверки гипотезы (G-square – близкий к критерию хи-квадрат по смыслу статистический критерий, только рассчитываемый с помощью методов максимального правдоподобия) — в нашем случае, нельзя отвергнуть гипотезу о равенстве пропорций.

Значение Cramer's V — величина эффекта с доверительным интервалом; Goodman-Kruskal's lambda — значения показателя связи (по интерпретации схож с коэффициентом корреляции); Goodmak-Kruskal tau – расширение Phi-статистики на случай таблиц 2*k. Все строчки с прочерком — пустые, потому что соответствующие значения рассчитываются только для таблиц 2*2.

В первом же графике почти все то же самое, только там исходная таблица выведена:

Собственно, для таблиц 2*2 все также (проверим гипотезу о равенстве пропорций значений переменной «пол» для разных значений переменной «наличие детей»):

data <- unclass(table(Affairs$gender,Affairs$children))
res <- chisquare(data, plot.or=FALSE, reference.level=1, row.level=1)

Мы снова не можем отвергнуть нулевую гипотезу на уровне значимости 0.05.

Остальные графики показывают таблицу «идеальных» частот при равенстве пропорций, отклонение реальных значений от идеальных — позволяют «подсветить» самые аномальные значения, которые вносят наиболее сильный вклад в асимметрию пропорций:

В данном случае можно сказать, что число мужчин без детей должно было быть существенно больше для выполнения условий равенства пропорций.