Секунда теории
Гетероскедастичность – это ситуация, когда ошибка регрессии не удовлетворяет условию гомоскедастичности, т.е. дисперсия этой самой ошибки непостоянно. Это приводит при использовании метода наименьших квадратов к разным неприятным эффектам смещения значений оценок, что ставит под сомнение смысл всей проделанной на основании данного уравнения регрессии работы.
В странствиях по CRAN-у попался пакет skedastic, в котором реализованы 25 разных тестов гомоскедастичности – о нем и поговорим.
О тестах
Вдумчивый разбор математического основания всех реализованных тестов – это дело статьи в специализированном журнале, дело данной заметки – посмотреть, как они работают.
Возьмем из пакета UsingR данные о бриллиантах diamond и посмотрим уравнение регрессии (цена зависит от веса)
library(tidyverse)
library(ggplot2)
library(skedastic)
library(AER)
library(gvlma)
library(UsingR)
data(diamond)
ggplot(data = diamond, aes(x=carat, y=price)) + geom_point()
model_1 <- lm(price~carat, data=diamond)
summary(model_1)
gvlma(model_1)
ggplot(data = diamond, aes(x=carat, y=model_1$residuals)) + geom_point() + ylab("Error of model")
На графике видна классическая линейная зависимость. Соответствующая модель значима и даже (по версии пакета gvlma) все условия Гаусса-Маркова выполняются
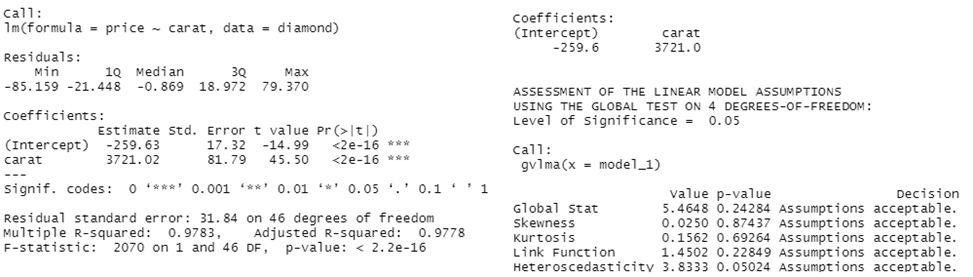
График ошибок говорит о том же самом:

Есть значительные основания полагать, что гетероскедастичности тут нет. Теперь посмотрим на результаты применения пакета skedastic (во всех тестах нулевая гипотеза: есть гомоскедастичность; при уровне значимости меньше заданного, допустим, 0.05, она будет отвергнута):

Собственно, тесты почти единодушны: 24 из 25 (кроме теста Хонды) указали, что нулевая гипотеза не может быть отвергнута, значит, можно смело говорить про гомоскедастичность.
Эксперимент
Самое интересное, правда, другое – вопрос о том, насколько эти тесты определяют гетероскедастичность, когда у нас она есть. Создадим искусственный датафрейм по формуле y = ax+b+e(1+s|x|) при разных значениях s. При s=0 у нас классическая гомоскедастичность (ошибки происходят из нормального распределения), при s=1 – классическая гетероскедастичность (когда дисперсия ошибок растет при увеличении х по модулю). Логично предположить, что нормальное поведение теста в этих случаях – обратная пропорциональность p-значения от значения s. Каждый тест проводился 100 раз на разных значениях a и b, его результаты потом усреднялись. Соответствующие графики представлены ниже:
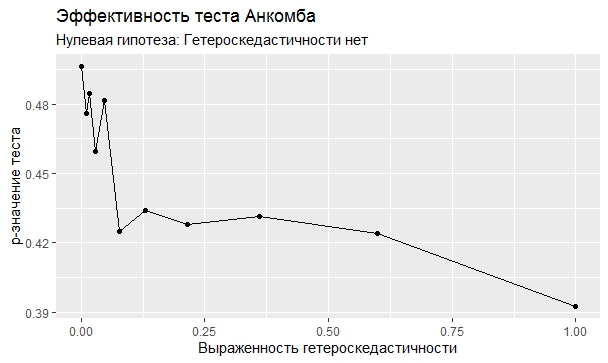
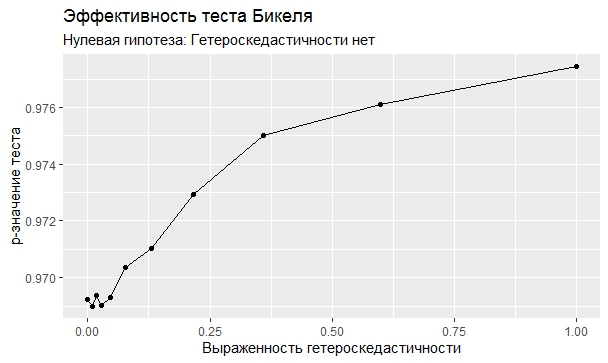
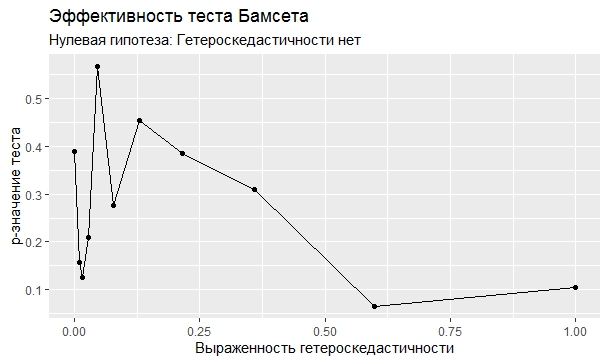

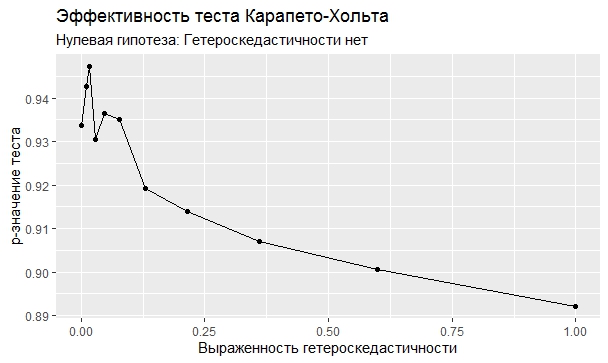
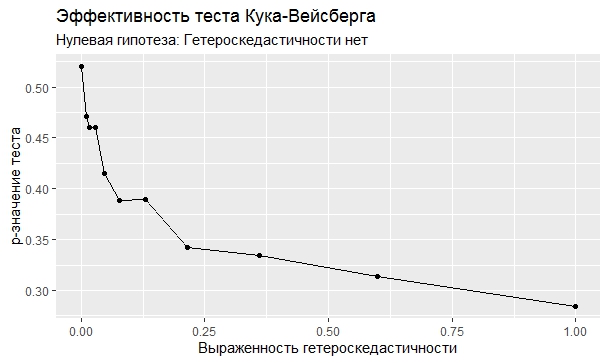
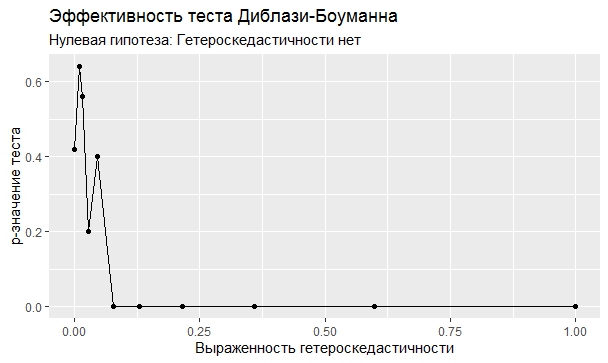
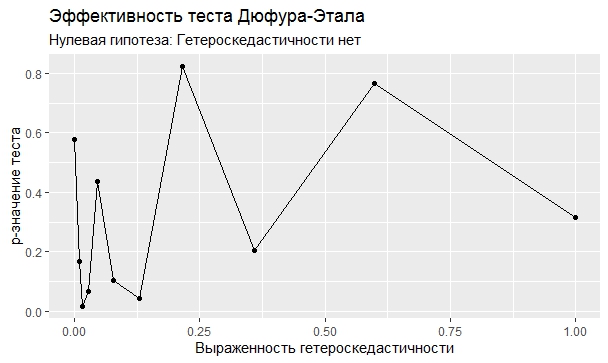
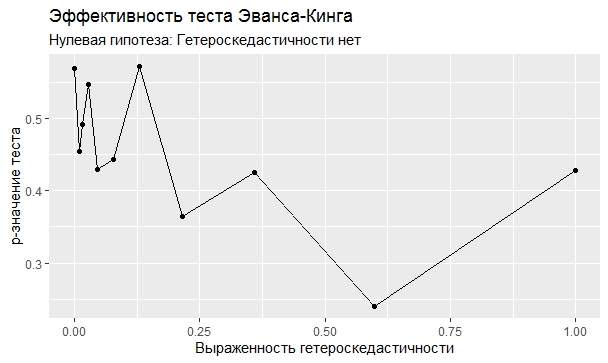
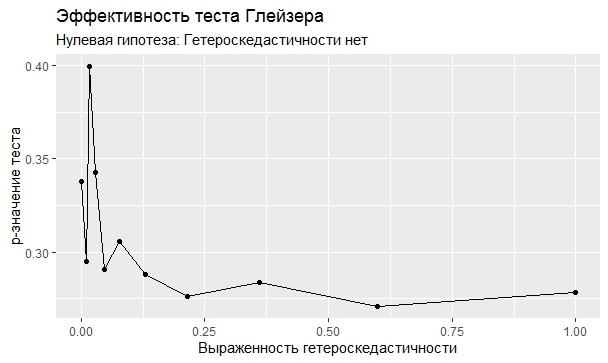
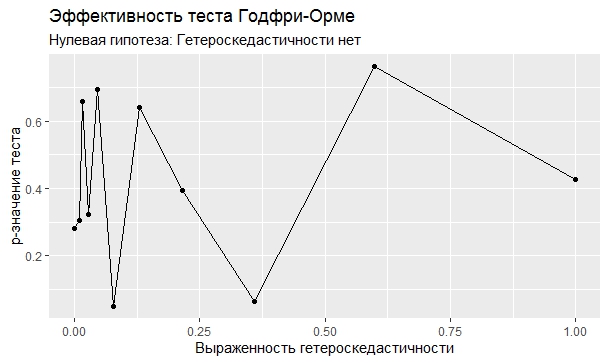
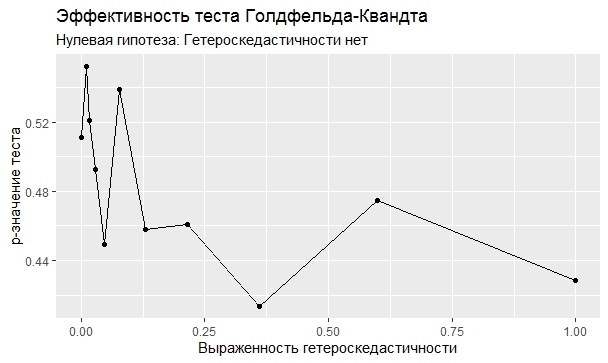
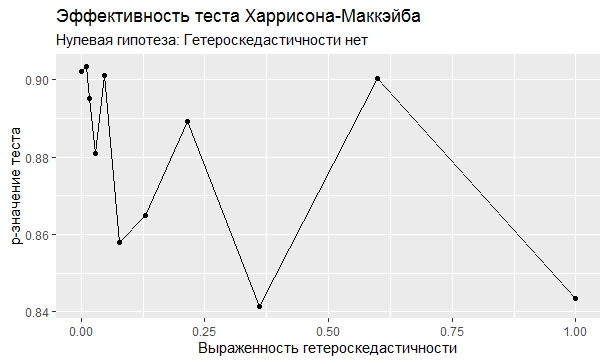
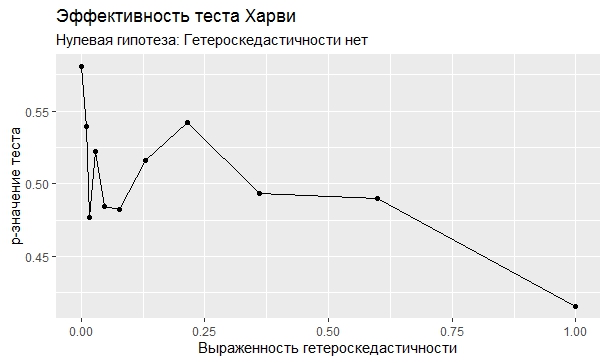
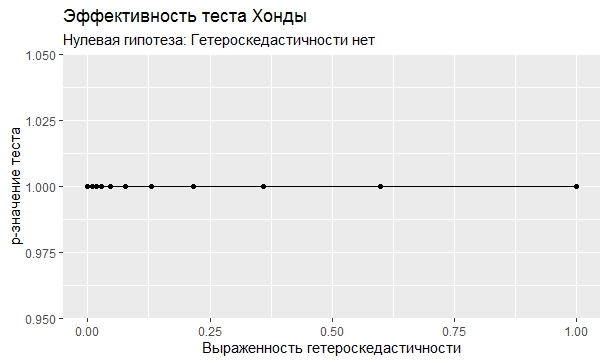
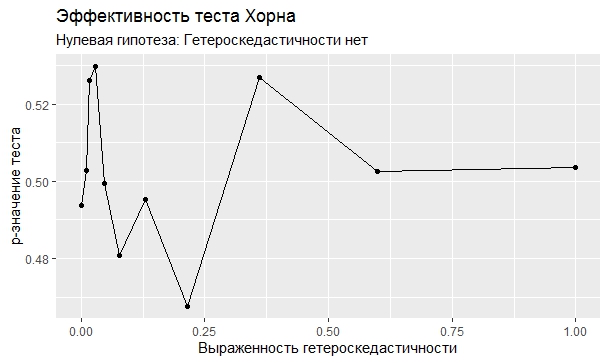
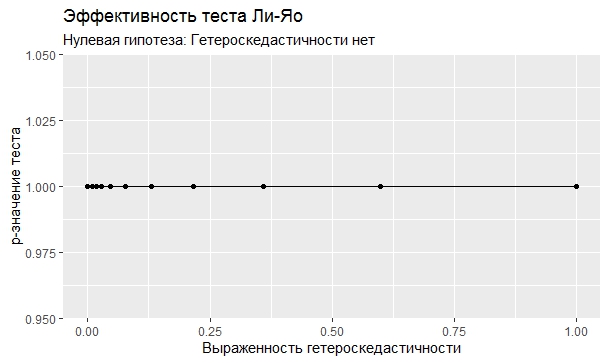
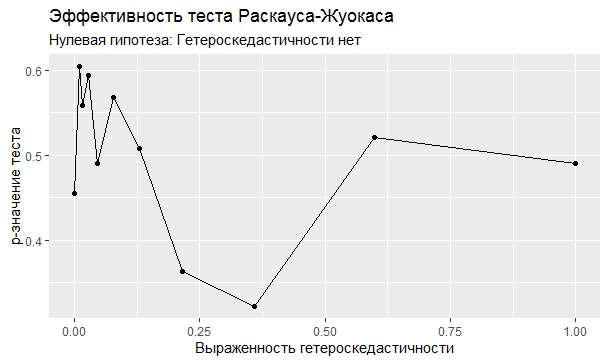
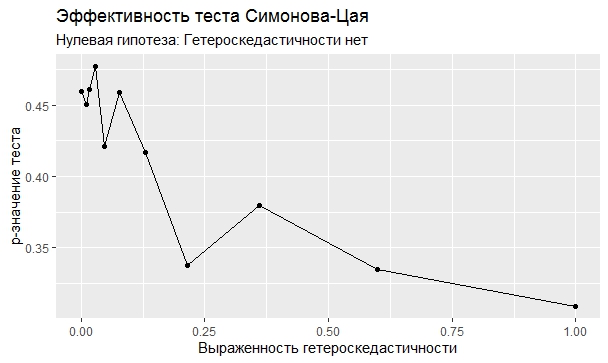
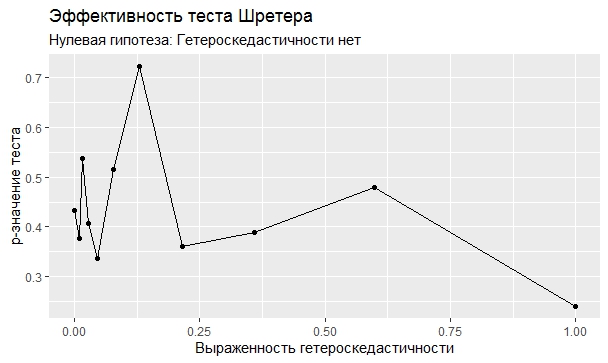
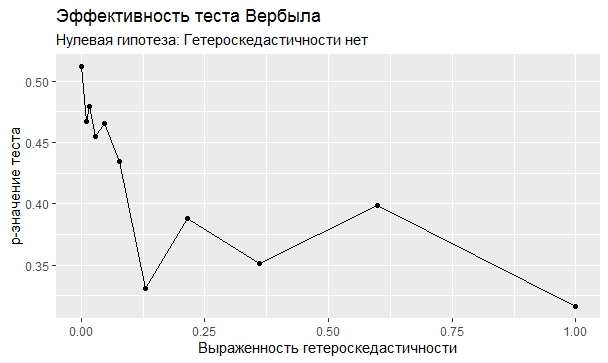
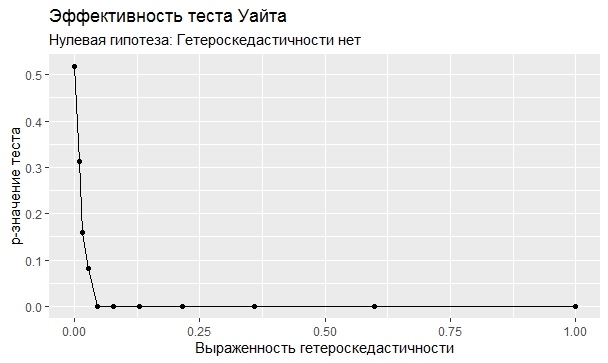
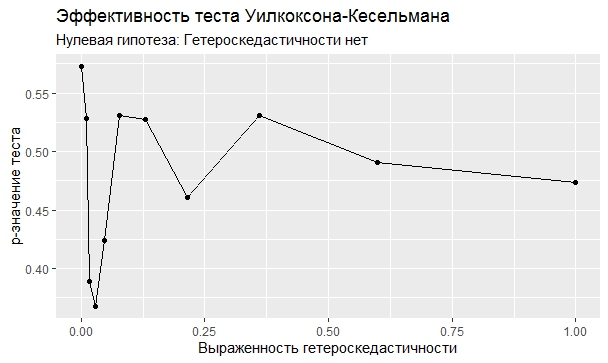
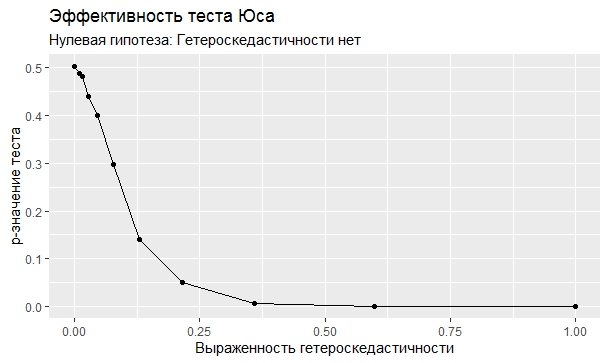
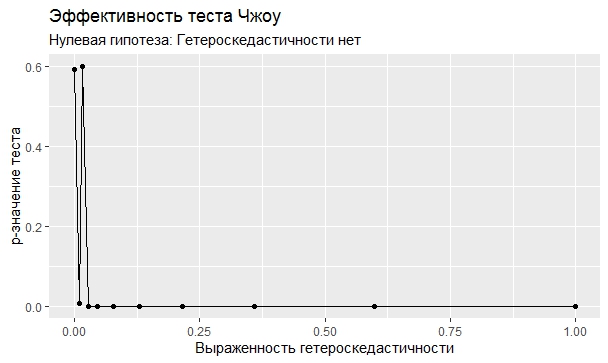
Собственно, тестов, определяющий данный вид гетероскедастичности, всего 4 (из 25): Диблази-Боуманна, Уайта, Юса и Чжоу. Это говорит о том, что даже если вам тесты показали, что у вас все хорошо, это не значит, что оно так и есть. И это также повод внимательно посмотреть и определить области эффективности этих тестов.
Все материалы, в т.ч. статьи авторов-изобретателей тестов, есть на https://github.com/acheremuhin/Heteroscedacity
Комментарии (3)

adeshere
26.07.2022 15:01Кто-то что-нибудь понял?
Картинки говорят сами за себя, но статья могла бы быть гораздо понятнее (и полезнее для очень многих читателей), если добавить в ее начало преамбулу про анализ остатков, т.е. ошибок аппроксимации данных какой-то моделью. Обычно модель можно считать хорошей, если эти ошибки не только малы, но и случайны. Множество математических методов в том или ином виде опираются на гипотезу о случайности шумов и, соответственно, ошибок. Поэтому если вдруг выясняется, что ошибки не случайны, то это серьезный повод задуматься про адекватность модели. Вот простой пример: пусть некоторая величина меняется по параболическому закону, а мы видим только результат измерений и пытаемся аппроксимировать эту зависимость прямой линией. Зашумленный фрагмент параболы может быть очень похож на прямую, но если посмотреть на остатки аппроксимации, то там будет виден явный "зигзаг", что сразу же наведет на мысль о недостаточности линейной модели.
Вот нарисовал пару иллюстраций
прямо на своем "рабочем столе", даже не подбирая параметры (если поварьировать кривизну параболы, амплитуду шума и число точек данных, то можно сделать гораздо нагляднее):
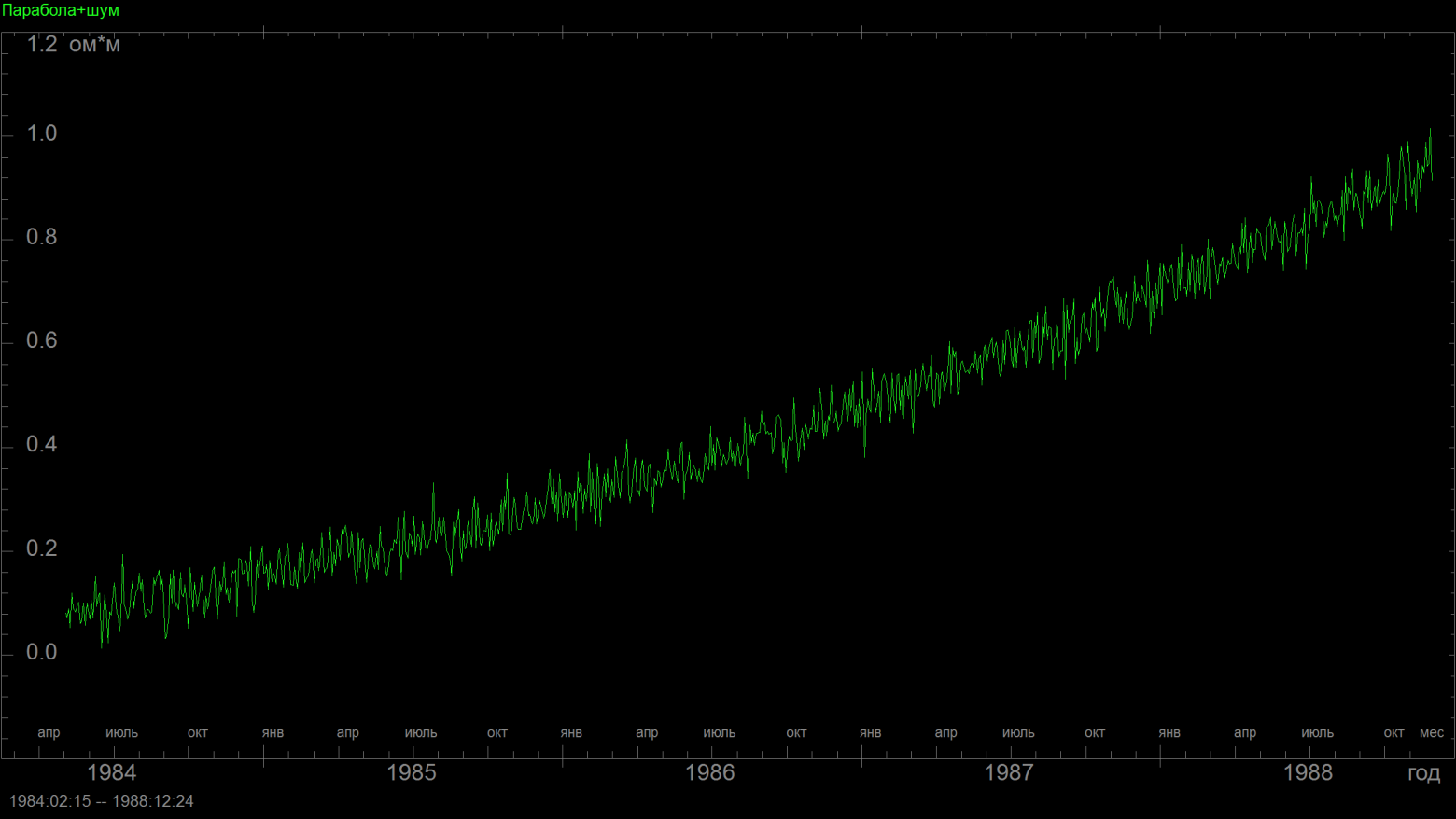
Это фрагмент параболы с шумом, - график довольно похож на линейный рост.
А вот параметры линейной аппроксимации:
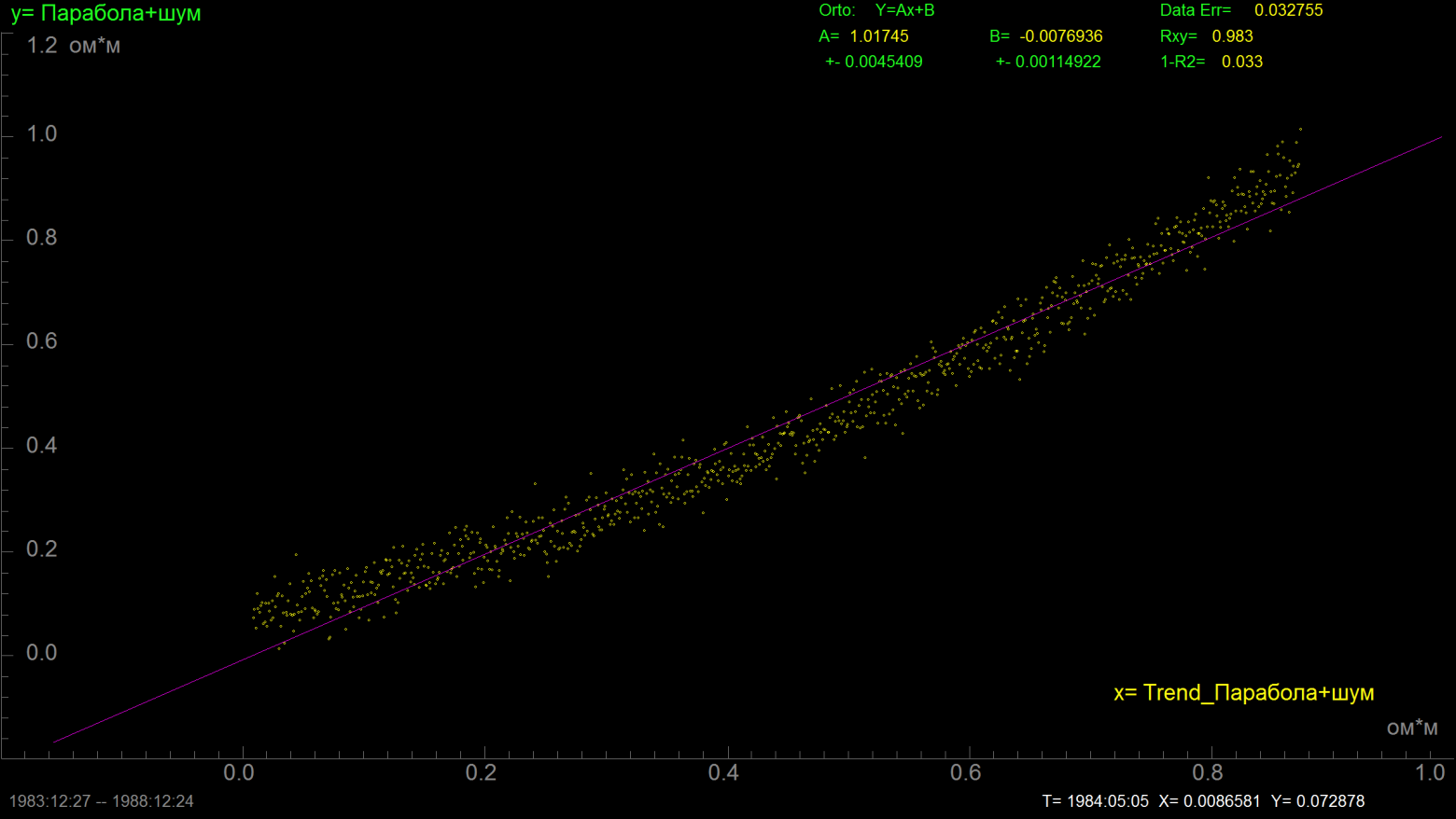
Коэффициент корреляции 0.983, 1-R^2=0.033, линейная модель объясняет более 98% дисперсии сигнала... она почти идеальна? Но посмотрим-ка теперь на график остатков:
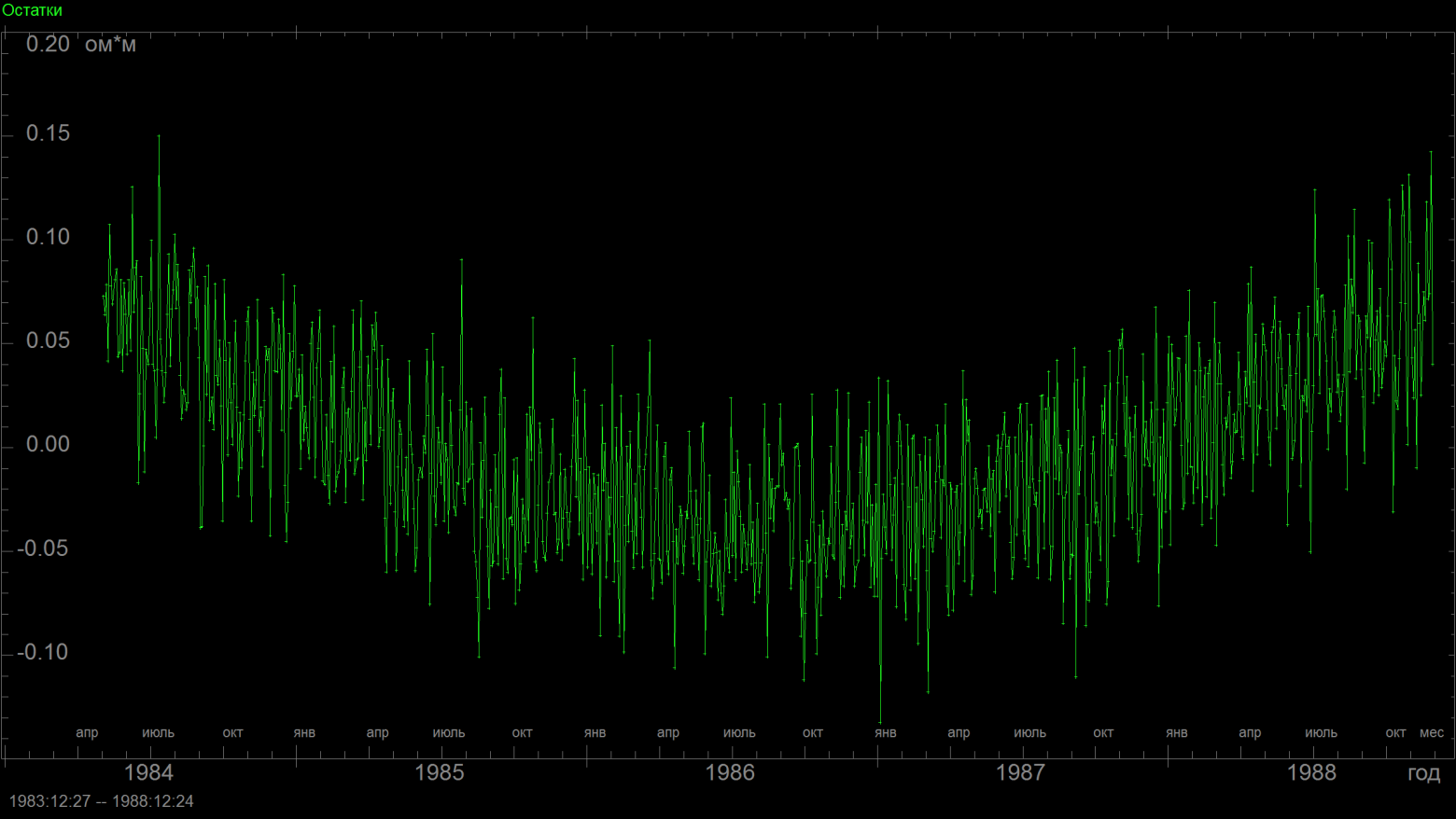
По нему сразу же видно, что в данных есть еще какая-то неучтенная, но абсолютно четкая динамика. Да, конечно, внимательный исследователь мог бы это заметить уже по первому графику, а тем более по второму. Но когда у тебя сотни таких рядов, то часто на изучение таких подробностей нет времени. Картинки листаются со скоростью прокрутки экрана... потом чуть внимательнее смотрим на таблицу со значениями на 1-R^2, где все почти на нуле... все нормально?
А вот график остатков даже при самом беглом просмотре не оставляет ни малейших сомнений, что с моделью что-то не так ;-)
Ну а теперь самое главное: неслучайность остатков может быть самой разной. То есть там может присутствовать не только динамика (закономерное изменение) средних значений, но и динамика дисперсии. В частности, дисперсия остатков сплошь и рядом будет расти со временем, если ряд имеет тенденцию к экспоненциальному росту, а амплитуда флуктуаций пропорциональна текущему уровню (а это типичнейшая ситуация в эконометрике). Поэтому при построении любых моделей и аппроксимаций очень важно не просто оценивать погрешность модели, но и анализировать остатки на предмет выявления там скрытых (неучтенных моделью) зависимостей и закономерностей. Собственно, обсуждаемая статья именно этому и посвящена. Поэтому мне очень жаль, что она написана в расчете на крайне узкого специалиста, а у большинства остальных читателей возникает впечатление "ничего не понятно". Тема-то ведь важная и полезная...
А еще для законченности и завершенности в статье не хватает хотя бы беглого пояснения основных идей, на которые опираются тесты Диблази-Боуманна, Уайта, Юса и Чжоу. Как рассчитывается критическая статистика теста, и почему она хорошо реагирует на отсутствие гетероскедастичности? Подчеркну: не хватает не формул для расчета статистик (они легко ищутся), а именно внятного, на пальцах, описания идей. Ведь базовые идеи у практически всех статистик весьма ясные и понятные. Вообще, сейчас довольно модно начинать изучение анализа данных с освоения программ и обучения правильному порядку "нажимания кнопок". При этом математика, которая стоит за всем этим, иногда кажется сложной и непонятной. Хотя на самом деле там все очень просто! Точнее, формулы могут быть очень заумными, но вот стоящие за ними идеи - почти всегда просты и прозрачны. Но понять эти идеи, просто читая инструкции к программе, можно далеко не всегда. Тут как никогда важен диалог с преподавателем (лектором). Именно этим и хороши многие хабросстатьи, что они "про идеи", а потом в обсуждении - диалог.
Поэтому, во-первых, спасибо Артему @acheremuhin за его цикл статей по статистике. А во-вторых, большая просьба к нему же не забывать рассказывать про идеи, прежде чем придавливать читателя полезными, но не всегда простыми для понимания фактами ;-)

acheremuhin Автор
26.07.2022 15:09+1Спасибо за комментарии и замечания. Я попробовал в черновике начать про идеи - но получалось очень много, и я решил в заметке не писать. Но внушение принято и понято, будем исправляться дальше.





Harrix
Кто-то что-нибудь понял?