Расскажу про алгоритм обучения с подкреплением Q-learning и его применении в сфере майнинга процессов. Алгоритм позволяет оптимизировать бизнес-процесс, превращая его из хаотичного графа, с большим количеством связей и ветвлений, в понятный и однозначный оптимальный путь исполнения.

Reinforcement Learning
Reinforcement Learning (RL) - одна из парадигм машинного обучения (ML). Основной задачей RL является обучение агентов, которые принимают решения и взаимодействуют с заданной средой. Оно происходит на основе системы наград, которые поощряют их за успешные решения. Такая формулировка задачи подходит для многих реальных задач – искусственный интеллект в компьютерных играх, контроль трафика, оптимизация путей и другие, в том числе и оптимизация бизнес-процессов, которые состоят из набора решений.
Q-Learning
Q-Learning является одним из наиболее простых в реализации RL методов. Он является model-free алгоритмом, то есть не основан на моделях. Некоторые исследователи пытаются дополнить идею с использованием методологии ML. Одним из результатов таких попыток является, например, архитектура Deep Q Networks. В данной статье рассматривается классический Q-learning.
Важной предпосылкой для такой оптимизации является Марковское свойство – каждое действие зависит исключительно от предыдущего. Это позволяет принимать решения на основе нескольких состояний, а не всего пути.
Обучение основывается на Q-таблице, которая для каждого состояния s и каждого возможного действия из этого состояния a хранит Q-значения. Q-таблица инициализируется нулями и заполняется в процессе обучения.
Заполнение таблицы происходит на основе решений агентов. Они могут выбирать действия с помощью exploitation и exploration. В режиме exploitation агенты выбирают действие с максимальным Q-значением:

При exploration действие выбирается случайно. Выбранным действием агент переходит в следующее состояние s’. Случайные выборы позволяют заполнять новые части таблицы.
Выбор между режимами происходит случайно. На практике вероятность exploitation устанавливают более высокой.
Обновление Q-таблицы происходит по формуле:
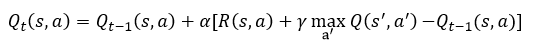
Выражение в квадратных скобках называется Temporal Difference. Оно включает в себя:
1. R(s, a) - награду за действие a в состоянии s
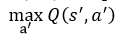
Q-значение в следующем состоянии s’. Выбор s’ происходит по описанной выше логике.
Будущие значения дисконтируются с коэффициентом

– таким образом близкие награды более важны, чем далекие, и результатом оптимизации является кратчайший путь до наибольшего значения.
Пример
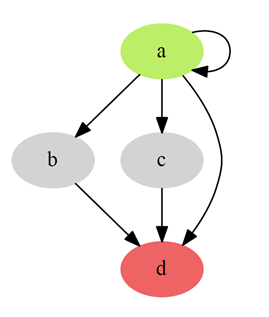
Рассмотрим простой пример. Мы хотим найти кратчайший путь из вершины, а (отмечена зеленым) в вершину d (отмечена красным) на некотором графе G:

Задаем вознаграждения: прохождение через существующее ребро будет стоить 15 единиц, а попадание в финальную вершину d – 999 единиц. При попадании в вершину d проход по графу будет останавливаться. Для простоты будет предполагать

Составим таблицу наград для агента:
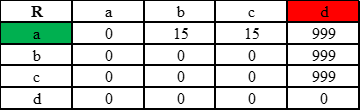
Инициализируем Q-таблицу нулями:
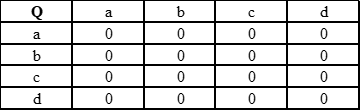
Первый проход фактически случаен. Пусть выбран путь <a, b, d>. Из-за нулевых Q значений агент заполняет таблицу значениями наград.
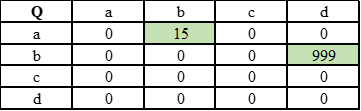
Далее при exploitation агенты выбирают путь <a, b, d>.
Ко второй итерации Q-значения сходятся.
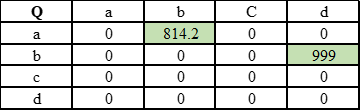
При случайном выборе пути <a, c, d> его значения сходятся таким же образом.
Далее агент выбирает случайно путь <a, d>. Тогда значение (a, d) заполняется следующим образом:
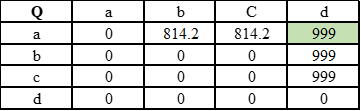
В режиме exploitation агент будет выбирать переход <a,d>.
Значения таблицы сошлись. Для поиска оптимального пути надо из вершины a через максимальные Q-значения прийти в вершину d.
Оптимальный путь - <a,d>.
Финальный граф выглядит так:
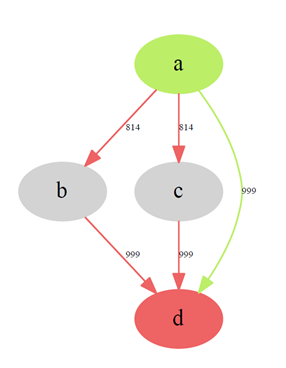
Недостижимые вершины и циклы
Недостижимые вершины можно исключать на этапе выбора действия или выучить их с помощью отрицательных наград. На этапе exploitation агенты не будут проходить через несуществующие ребра за счет их низкого Q-значения. Дополнительно, в задачах часто вводится штраф за циклы в пути.
Python реализация
Для начала необходимо создать матрицу Q-значений и матрицу наград. Для демонстрации утверждений выше добавим в граф G цикл в вершине a – назовем его G’.
import numpy as np
# Дизайн наград
cycle_fine = -60 # Штраф за цикл
absence_fine = -999 # Штраф за несуществующий переход
step_reward = 15 # Награда за существующий переход
finish_reward = 999 # Награда за завершение
# Матрица ребер графа
adjacency_matrix = np.array([[1, 1, 1, 1],
[0, 0, 0, 1],
[0, 0, 0, 1],
[0, 0, 0, 0]])
# Инициализируем обе матрицы нулями
reward_matrix = np.zeros_like(adjacency_matrix)
q_matrix = np.zeros_like(adjacency_matrix) # Заполняется алгоритмом
# Заполняем матрицу наград
mask = (adjacency_matrix != 0)
# Заполняем наградой за прохождение существующие ребра
reward_matrix[mask] = step_reward
# Заполняем значениями существующие переходы в финальное состояние
reward_matrix[:, -1][mask[:, -1]] = finish_reward
# Заполняем несуществующие переходы штрафом за отсутствие
reward_matrix[~mask] = absence_fine
# Заполняем имеющиеся циклы штрафом за циклы, циклы которых нет в adjacency_matrix заполняем штрафом за отсутствие
diagonal_mask = np.diagonal(adjacency_matrix != 0)
diagonal_values = cycle_fine * diagonal_mask
diagonal_values += absence_fine * ~diagonal_mask
np.fill_diagonal(reward_matrix, diagonal_values)
Результат выполнения:
array([[ -60, 15, 15, 999],
[-999, -999, -999, 999],
[-999, -999, -999, 999],
[-999, -999, -999, -999]])
Далее матрицу наград и Q-матрицу можно подать в алгоритм обучения.
# Обучение
# Заполняем Q-значения
import random
epochs = 1000
eps = 0.2 # Доля exploration
alpha = 1 # Скорость обучения
gamma = 0.8 # Коэффициент дисконтирования
num_states = reward_matrix.shape[1] - 1
for i in range(epochs): # Количество прогонов
# Засчитываем окончание, когда происходит переход в последний столбец таблицы
state = 0
while state != num_states:
eps_hat = random.uniform(0, 1) # Случайная величина, на основе которой выбирается режим
if eps_hat < eps:
# Exploration
action = np.random.choice(range(0, num_states + 1))
else:
# Exploitation
action = np.argmax(q_matrix[state, :])
# Заполняем Q-таблицу в соответствии с формулой
q_matrix[state, action] += alpha * (reward_matrix[state, action] + \
gamma * np.max(q_matrix[action, :]) \
- matrix[state, action])
state = action
После 1000 итераций матрица сошлась:
array([[ 739, 814, 814, 999],
[-199, -199, -199, 999],
[-199, -199, -199, 999],
[ 0, 0, 0, 0]])
Получаем граф, который выглядит следующим образом:
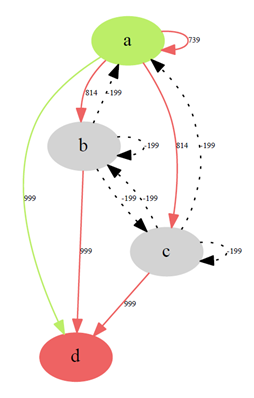
Чтобы найти оптимальный путь сделаем проход по максимальным значениям Q-матрицы.
state = 0
print(state, end = "->")
while state != num_states:
action = np.argmax(q_matrix[state, :])
print(action, end = "->")
state = action
print("end")
0->3->end
Вывод 0 -> 3 соответствует пути <a,d>, который является оптимальным решением задачи.
Process Mining
Одним из основных методов майнинга процессов является представление лога в виде графа процесса. Лог – набор данных, который содержит некоторое количество описаний выполнения одного и того же процесса. Лог содержит стадии процесса, время выполнения отдельных стадий, время между стадиями, исполнителя и другие характеристики процесса.
Графы бизнес-процесса выглядят крайне запутано – имеют большое количество связей, вершин, циклов и бутылочных горлышек (стадий, которые могут замедлять процесс). В виде графа процесс может быть подан в Q-learning. Наиболее простой случай – поиск кратчайшего пути в процессе. Такой алгоритм, например, реализован в программной среде SberPM. Развить алгоритм можно через использование времени выполнения ребра или других признаков в наградах.
Q-learning достаточно тяжелый с вычислительной точки зрения – его вычислительная сложность
Он может быть заменен на более легковесные алгоритмы для поиска кратчайшего пути. Q-learning однако создает матрицу с наградами, которая может быть использована для представления субоптимальных, но близких к оптимуму ветвей процесса или нескольких оптимумов.

