К старту флагманского курса по Data Science реализуем и сравним свёрточную сеть и сеть с механизмом самовнимания. С помощью t-SNE покажем, что и каким образом изучается в графовой сети с механизмом самовнимания. За подробностями приглашаем под кат.

Графовые сети внимания по вполне понятным причинам — один из самых популярных типов графовых нейросетей. В графовых свёрточных сетях у всех соседних узлов важность одинаковая. Очевидно, что так быть не должно.

Эта проблема решается в графовых сетях с механизмом внимания. Чтобы учесть важность каждого соседнего узла, механизмом внимания каждому соединению присваивается весовой коэффициент.

Рассчитаем весовые коэффициенты и реализуем в PyTorch Geometric эффективную графовую сеть с механизмом внимания. Запустить код этого руководства можно в блокноте Google Colab.

Графовые данные

Для наших целей есть три классических набора графовых данных. Это сети научных работ, где каждое соединение узлов — цитата из научной работы.

• Cora. Состоит из 2708 работ по машинному обучению в одной из семи категорий. Признаки узла — наличие (1) или отсутствие (0) в работе 1433 элементов набора слов. Иными словами, речь идёт о бинарном «мешке слов».

• CiteSeer. Аналогичный набор данных из 3312 научных работ для классификации в одну из шести категорий. Признаки узла — наличие (1) или отсутствие (0) в работе элементов набора из 3703 слов.

• PubMed. Это набор данных из 19 717 научных публикаций о диабете из базы данных PubMed из трёх категорий. Признаки узла — взвешенные по TF-IDF векторы слов из словаря на 500 уникальных слов.

Эти наборы данных широко применялись в научном сообществе. Используя многослойные персептроны (MLP), графовые свёрточные сети (GCN) и графовые сети с механизмом внимания (GAT), сравним наши показатели точности с указанными в литературе:

Набор данных PubMed довольно большой, его обработка и обучение на нём графовой нейросети продлятся дольше. Cora — самый изученный в литературе. Поэтому возьмём CiteSeer как усреднённый вариант.

С помощью класса Planetoid в PyTorch Geometric можно напрямую импортировать любой из этих наборов данных:

from torch_geometric.datasets import Planetoid

# Import dataset from PyTorch Geometric
dataset = Planetoid(root=".", name="CiteSeer")

# Print information about the dataset
print(f'Number of graphs: {len(dataset)}')
print(f'Number of nodes: {dataset[0].x.shape[0]}')
print(f'Number of features: {dataset.num_features}')
print(f'Number of classes: {dataset.num_classes}')
print(f'Has isolated nodes: {dataset[0].has_isolated_nodes()}')

Number of graphs: 1
Number of nodes: 3327
Number of features: 3703
Number of classes: 6
Has isolated nodes: True

У нас 3327 узлов вместо 3312. На самом деле в PyTorch Geometric используется реализация CiteSeer из этой работы, где тоже показаны 3327 узлов. Но часть узлов, а именно 48, изолирована! Корректно классифицировать их без агрегирования нелегко. Построим график числа соединений каждого узла с помощью degree:

from torch_geometric.utils import degree
from collections import Counter

# Get list of degrees for each node
degrees = degree(data.edge_index[0]).numpy()

# Count the number of nodes for each degree
numbers = Counter(degrees)

# Bar plot
fig, ax = plt.subplots(figsize=(18, 7))
ax.set_xlabel('Node degree')
ax.set_ylabel('Number of nodes')
plt.bar(numbers.keys(),
        numbers.values(),
        color='#0A047A')

У большинства узлов есть только 1 или 2 соседних. Этим можно объяснить меньшие показатели точности CiteSeer, чем у двух других наборов данных.

2. Самовнимание

Термин «самовнимание» в графовых нейросетях впервые появился в 2017 году в работе Veličković et al., когда за основу взяли простую идею: не у всех узлов должна быть одинаковая важность. И это не просто внимание, а самовнимание — здесь входные данные сравниваются друг с другом:

Этим механизмом каждому соединению присваивается весовой коэффициент (показатель внимания). Пусть αᵢⱼ — это показатель внимания между узлами i и j. Вот как вычисляется встраивание узла 1, где ????— это общая весовая матрица:

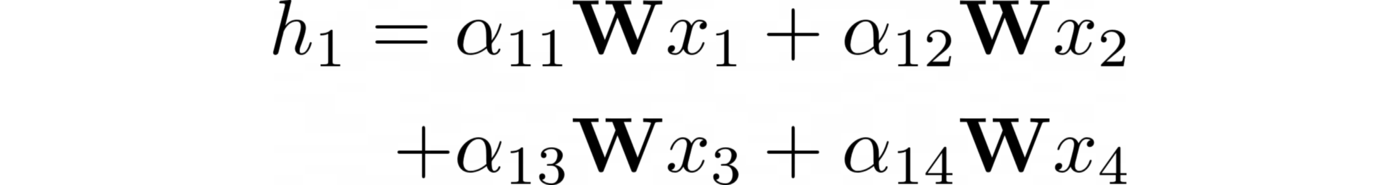
Но как рассчитать показатели внимания? Можно написать статическую формулу, но разумнее узнать их значения с помощью нейросети. Решение состоит из этих этапов:

1. Линейное преобразование.

2. Функция активации.

3. Нормализация Softmax.

Линейное преобразование

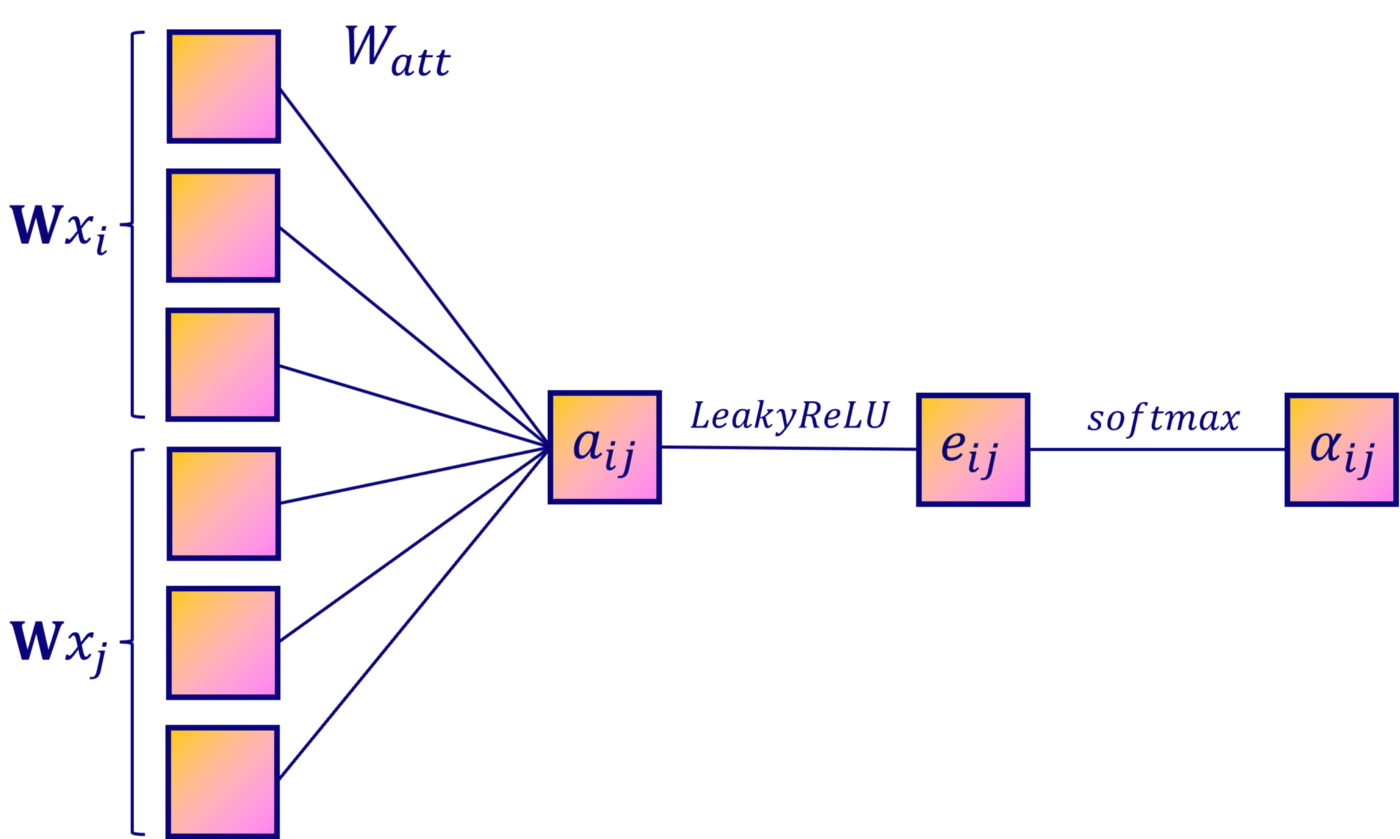
Чтобы вычислить важность каждого соединения, нужны пары скрытых векторов. Проще всего конкатенировать эти векторы из обоих узлов. Только тогда можно применить новое линейное преобразование с весовой матрицей ????ₐₜₜ:

Функция активации

Мы создаём нейросеть, поэтому второй этап — добавление функции активации. В данном случае авторы работы выбрали функцию LeakyReLU:

Нормализация Softmax

Чтобы сравнить показатели, выходные данные нейросети нужно нормализовать. И, чтобы определить, какой узел: 2 или 3 (α₁₂ > α₁₃), важнее для узла 1, узлам нужен одинаковый масштаб. В нейросетях для этого часто используют функцию softmax. Применим её к каждому соседнему узлу:

Так вычисляется каждый αᵢⱼ. Но самовнимание не очень стабильно. Чтобы повысить производительность, авторы Vaswani et al. ввели в архитектуре Transformer понятие «многоголовое внимание».

Бонус: многоголовое внимание

Удивительно, как много было сказано о самовнимании, хотя Transformer на самом деле — графовые нейросети, поэтому здесь применимы идеи из обработки естественного языка:

То есть в графовых сетях с механизмом внимания многоголовое внимание проявляется в многократном повторении тех же трёх этапов, чтобы усреднить или конкатенировать результаты. 

Вот и всё. Вместо одного h₁ получаем один скрытый вектор h₁ᵏ на каждую голову внимания. Дальше применяется одна из двух схем:

• Разные hᵢᵏ суммируются и результат нормализуется на количество голов внимания n — это усреднение.

• Объединение разных hᵢᵏ — конкатенация:

На практике первая схема применяется на выходном слое сети, вторая — на скрытом слое.

Графовые сети внимания

Реализуем графовую сеть с механизмом внимания в PyTorch Geometric. В этой библиотеке есть два слоя графового внимания: GATConv и GATv2Conv. До сих пор речь шла о первом из них, но в 2021 году Brody et al. добились улучшения, поменяв порядок операций. 

Весовая матрица ???? применяется после конкатенации, а весовая матрица внимания ????ₐₜₜ — после функции LeakyReLU. В итоге имеем:

• GatConv:

• Gatv2Conv:

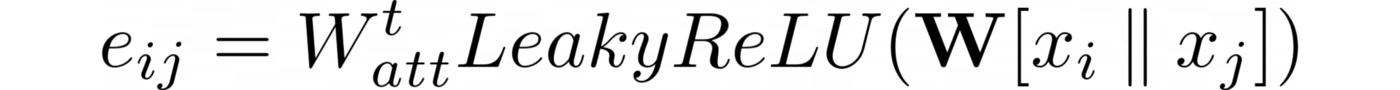
Какой слой использовать? В работе Brody et al. сказано, что Gatv2Conv неизменно превосходит GatConv.

А теперь классифицируем работы из CiteSeer. Я попытался примерно воспроизвести эксперименты авторов оригинала, излишне не усложняя их. Официальная реализация графовой сети с механизмом внимания есть на GitHub.

Слои графового внимания использованы в двух конфигурациях:

• в первом слое конкатенируются восемь выходных нейронов — это многоголовое внимание;

• во втором голова только одна, в ней и вычисляются окончательные встраивания.

Чтобы сравнить показатели точности, обучим и протестируем графовую свёрточную сеть:

import torch.nn.functional as F
from torch.nn import Linear, Dropout
from torch_geometric.nn import GCNConv, GATv2Conv


class GCN(torch.nn.Module):
  """Graph Convolutional Network"""
  def __init__(self, dim_in, dim_h, dim_out):
    super().__init__()
    self.gcn1 = GCNConv(dim_in, dim_h)
    self.gcn2 = GCNConv(dim_h, dim_out)
    self.optimizer = torch.optim.Adam(self.parameters(),
                                      lr=0.01,
                                      weight_decay=5e-4)

  def forward(self, x, edge_index):
    h = F.dropout(x, p=0.5, training=self.training)
    h = self.gcn1(h, edge_index)
    h = torch.relu(h)
    h = F.dropout(h, p=0.5, training=self.training)
    h = self.gcn2(h, edge_index)
    return h, F.log_softmax(h, dim=1)


class GAT(torch.nn.Module):
  """Graph Attention Network"""
  def __init__(self, dim_in, dim_h, dim_out, heads=8):
    super().__init__()
    self.gat1 = GATv2Conv(dim_in, dim_h, heads=heads)
    self.gat2 = GATv2Conv(dim_h*heads, dim_out, heads=1)
    self.optimizer = torch.optim.Adam(self.parameters(),
                                      lr=0.005,
                                      weight_decay=5e-4)

  def forward(self, x, edge_index):
    h = F.dropout(x, p=0.6, training=self.training)
    h = self.gat1(x, edge_index)
    h = F.elu(h)
    h = F.dropout(h, p=0.6, training=self.training)
    h = self.gat2(h, edge_index)
    return h, F.log_softmax(h, dim=1)

def accuracy(pred_y, y):
    """Calculate accuracy."""
    return ((pred_y == y).sum() / len(y)).item()

def train(model, data):
    """Train a GNN model and return the trained model."""
    criterion = torch.nn.CrossEntropyLoss()
    optimizer = model.optimizer
    epochs = 200

    model.train()
    for epoch in range(epochs+1):
        # Training
        optimizer.zero_grad()
        _, out = model(data.x, data.edge_index)
        loss = criterion(out[data.train_mask], data.y[data.train_mask])
        acc = accuracy(out[data.train_mask].argmax(dim=1), data.y[data.train_mask])
        loss.backward()
        optimizer.step()

        # Validation
        val_loss = criterion(out[data.val_mask], data.y[data.val_mask])
        val_acc = accuracy(out[data.val_mask].argmax(dim=1), data.y[data.val_mask])

        # Print metrics every 10 epochs
        if(epoch % 10 == 0):
            print(f'Epoch {epoch:>3} | Train Loss: {loss:.3f} | Train Acc: '
                  f'{acc*100:>6.2f}% | Val Loss: {val_loss:.2f} | '
                  f'Val Acc: {val_acc*100:.2f}%')
          
    return model

def test(model, data):
    """Evaluate the model on test set and print the accuracy score."""
    model.eval()
    _, out = model(data.x, data.edge_index)
    acc = accuracy(out.argmax(dim=1)[data.test_mask], data.y[data.test_mask])
    return acc

%%time

# Create GCN
gcn = GCN(dataset.num_features, 16, dataset.num_classes)
print(gcn)

# Train
train(gcn, data)

# Test
acc = test(gcn, data)
print(f'GCN test accuracy: {acc*100:.2f}%\n')

GCN(
  (gcn1): GCNConv(3703, 16)
  (gcn2): GCNConv(16, 6)
)
Epoch   0 | Train Loss: 1.782 | Train Acc:  20.83% | Val Loss: 1.79 
Epoch  20 | Train Loss: 0.165 | Train Acc:  95.00% | Val Loss: 1.30 
Epoch  40 | Train Loss: 0.069 | Train Acc:  99.17% | Val Loss: 1.66 
Epoch  60 | Train Loss: 0.053 | Train Acc:  99.17% | Val Loss: 1.50 
Epoch  80 | Train Loss: 0.054 | Train Acc: 100.00% | Val Loss: 1.67 
Epoch 100 | Train Loss: 0.062 | Train Acc:  99.17% | Val Loss: 1.62 
Epoch 120 | Train Loss: 0.043 | Train Acc: 100.00% | Val Loss: 1.66 
Epoch 140 | Train Loss: 0.058 | Train Acc:  98.33% | Val Loss: 1.68 
Epoch 160 | Train Loss: 0.037 | Train Acc: 100.00% | Val Loss: 1.44 
Epoch 180 | Train Loss: 0.036 | Train Acc:  99.17% | Val Loss: 1.65 
Epoch 200 | Train Loss: 0.093 | Train Acc:  95.83% | Val Loss: 1.73 

GCN test accuracy: 67.70%

CPU times: user 25.1 s, sys: 847 ms, total: 25.9 s
Wall time: 32.4 s

%%time

# Create GAT
gat = GAT(dataset.num_features, 8, dataset.num_classes)
print(gat)

# Train
train(gat, data)

# Test
acc = test(gat, data)
print(f'GAT test accuracy: {acc*100:.2f}%\n')

GAT(
  (gat1): GATv2Conv(3703, 8, heads=8)
  (gat2): GATv2Conv(64, 6, heads=1)
)
Epoch   0 | Train Loss: 1.790 | Val Loss: 1.81 | Val Acc: 12.80%
Epoch  20 | Train Loss: 0.040 | Val Loss: 1.21 | Val Acc: 64.80%
Epoch  40 | Train Loss: 0.027 | Val Loss: 1.20 | Val Acc: 67.20%
Epoch  60 | Train Loss: 0.009 | Val Loss: 1.11 | Val Acc: 67.00%
Epoch  80 | Train Loss: 0.013 | Val Loss: 1.16 | Val Acc: 66.80%
Epoch 100 | Train Loss: 0.013 | Val Loss: 1.07 | Val Acc: 67.20%
Epoch 120 | Train Loss: 0.014 | Val Loss: 1.12 | Val Acc: 66.40%
Epoch 140 | Train Loss: 0.007 | Val Loss: 1.19 | Val Acc: 65.40%
Epoch 160 | Train Loss: 0.007 | Val Loss: 1.16 | Val Acc: 68.40%
Epoch 180 | Train Loss: 0.006 | Val Loss: 1.13 | Val Acc: 68.60%
Epoch 200 | Train Loss: 0.007 | Val Loss: 1.13 | Val Acc: 68.40%

GAT test accuracy: 70.00%

CPU times: user 53.4 s, sys: 2.68 s, total: 56.1 s
Wall time: 55.9 s

Этот эксперимент не строгий: его нужно повторять n раз и за конечный результат принять среднюю точность со стандартным отклонением.

В этом примере сеть с механизмом внимания превосходит свёрточную по точности (70,00% против 67,70), но требует больше времени на обучение, то есть 55,9 секунд против 32,4, что может вызвать проблемы с масштабируемостью при работе с большими графами.

Авторы получили 72,5% на сети с механизмом внимания и 70,3% для свёрточной сети, что явно лучше наших результатов. Разницу можно объяснить настройками параметров в моделях, а также настройками обучения (например, patience 100 вместо фиксированного количества эпох.

Итак, чему научилась сеть с механизмом внимания? Используем мощный метод t-SNE для построения данных высокой размерности в 2D или 3D. Сначала посмотрим, как выглядели встраивания до обучения: как создающиеся из случайно инициализированных весовых матриц они должны быть абсолютно случайными:

untrained_gat = GAT(dataset.num_features, 8, dataset.num_classes)

# Get embeddings
h, _ = untrained_gat(data.x, data.edge_index)

# Train TSNE
tsne = TSNE(n_components=2, learning_rate='auto',
         init='pca').fit_transform(h.detach())

# Plot TSNE
plt.figure(figsize=(10, 10))
plt.axis('off')
plt.scatter(tsne[:, 0], tsne[:, 1], s=50, c=data.y)
plt.show()

Действительно, никакой явной структуры здесь нет. Но лучше ли выглядят встраивания, созданные из обученной модели?

h, _ = gat(data.x, data.edge_index)

# Train TSNE
tsne = TSNE(n_components=2, learning_rate='auto',
         init='pca').fit_transform(h.detach())

# Plot TSNE
plt.figure(figsize=(10, 10))
plt.axis('off')
plt.scatter(tsne[:, 0], tsne[:, 1], s=50, c=data.y)
plt.show()

Разница заметна: узлы одного класса собраны вместе. Видны шесть кластеров, соответствующих шести классам работ. Есть отклоняющиеся значения, но этого следовало ожидать: наш показатель точности далёк от идеала.

Ранее я предположил, что узлы с плохими соединениями могут негативно влиять на производительность CiteSeer. Рассчитаем точность модели для каждой связи узлов:

from torch_geometric.utils import degree

# Get model's classifications
_, out = gat(data.x, data.edge_index)

# Calculate the degree of each node
degrees = degree(data.edge_index[0]).numpy()

# Store accuracy scores and sample sizes
accuracies = []
sizes = []

# Accuracy for degrees between 0 and 5
for i in range(0, 6):
  mask = np.where(degrees == i)[0]
  accuracies.append(accuracy(out.argmax(dim=1)[mask], data.y[mask]))
  sizes.append(len(mask))

# Accuracy for degrees > 5
mask = np.where(degrees > 5)[0]
accuracies.append(accuracy(out.argmax(dim=1)[mask], data.y[mask]))
sizes.append(len(mask))

# Bar plot
fig, ax = plt.subplots(figsize=(18, 9))
ax.set_xlabel('Node degree')
ax.set_ylabel('Accuracy score')
ax.set_facecolor('#EFEEEA')
plt.bar(['0','1','2','3','4','5','>5'],
        accuracies,
        color='#0A047A')
for i in range(0, 7):
    plt.text(i, accuracies[i], f'{accuracies[i]*100:.2f}%',
             ha='center', color='#0A047A')
for i in range(0, 7):
    plt.text(i, accuracies[i]//2, sizes[i],
             ha='center', color='white')

И результаты подтверждают это предположение: узлы, у которых мало соседей, классифицировать сложнее. Таковы особенности графовых нейросетей: чем больше релевантных соединений, тем больше агрегируется информации.

Заключение

Хотя графовые сети внимания обучаются дольше, точность у них существенно выше, чем у графовых свёрточных сетей. Механизмом самовнимания вместо статических коэффициентов автоматически вычисляются весовые коэффициенты и встраивания оказываются точнее.

Графовые сети внимания — де-факто стандарт во многих задачах с применением графовых нейросетей. Однако большее время обучения может стать проблемой при работе с крупными наборами графовых данных. Масштабируемость в глубоком обучении важный фактор: обычно больший объём данных может привести к повышению производительности.

А мы поможем вам прокачать навыки или с самого начала освоить профессию, актуальную в любое время:

• Профессия Data Scientist

• Профессия Fullstack-разработчик на Python

Выбрать другую востребованную профессию.