23.04.2022 17:05
aabzel 29 7200 Источник

Существует классическая задача:

Есть 2 емкости: 5 литров и 3 литра. Как отмерить 4 литра жидкости используя только эти 2 емкости?

Понятное дело что тут важно не сколько знание правильного ответа, а знание метода решения таких задач. Ведь вместо целевых 4х литров могут спросить отсчитать и 1,2,6,7 литров.

В этом тексте я решу эту задачу в общем виде при помощи конечного автомата. Так как тут явно можно проследить состояния и входные воздействия. Также я упомяну про малоизвестный язык Front-End разметки Dot. Методика конечного автомата хорошо изучена и поставлена на рельсы. Состоит из 3 фаз.

Фаза №1: перечислить все возможные состояния (комбинаторика)

Состояние определяется количеством жидкости в паре сосудов. Согласно комбинаторике по правилу умножения существует всего 24 состояния. Вот они все перечислены.

Фаза №2 перечислить все возможные входы. (из условий задачи)

Существует всего 5 легальных действий с бутылками. Вот их перечень.

№
№

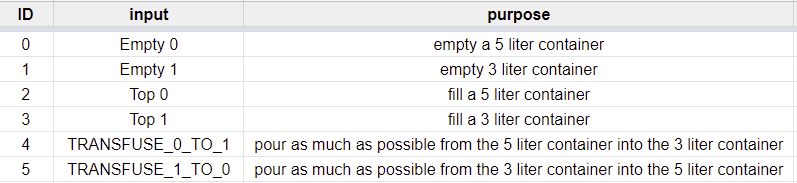
Фаза №3 составить таблицу переходов

+----+-----+-----+-----+-----+-----+-----+-----+
| #  |     |  E0 |  E1 |  T0 |  T0 | 0T1 | 1T0 |  
+----+-----+-----+-----+-----+-----+-----+-----+
| 1  | s00 | s00 | s00 | s50 | s03 | s00 | s00 |
| 2  | s01 | s01 | s00 | s51 | s03 | s01 | s10 |
| 3  | s02 | s02 | s00 | s52 | s03 | s02 | s20 |
| 4  | s03 | s03 | s00 | s53 | s03 | s03 | s30 |
| 5  | s10 | s00 | s10 | s50 | s13 | s01 | s10 |
| 6  | s11 | s01 | s10 | s51 | s13 | s02 | s20 |
| 7  | s12 | s02 | s10 | s52 | s13 | s03 | s30 |
| 8  | s13 | s03 | s10 | s53 | s13 | s13 | s40 |
| 9  | s20 | s00 | s20 | s50 | s23 | s02 | s20 |
| 10 | s21 | s01 | s20 | s51 | s23 | s03 | s30 |
| 11 | s22 | s02 | s20 | s52 | s23 | s13 | s40 |
| 12 | s23 | s03 | s20 | s53 | s23 | s23 | s50 |
| 13 | s30 | s00 | s30 | s50 | s33 | s03 | s30 |
| 14 | s31 | s01 | s30 | s51 | s33 | s13 | s40 |
| 15 | s32 | s02 | s30 | s52 | s33 | s23 | s50 |
| 16 | s33 | s03 | s30 | s53 | s33 | s33 | s51 |
| 17 | s40 | s00 | s40 | s50 | s43 | s13 | s40 |
| 18 | s41 | s01 | s40 | s51 | s43 | s23 | s50 |
| 19 | s42 | s02 | s40 | s52 | s43 | s33 | s51 |
| 20 | s43 | s03 | s40 | s53 | s43 | s43 | s52 |
| 21 | s50 | s00 | s50 | s50 | s53 | s23 | s50 |
| 22 | s51 | s01 | s50 | s51 | s53 | s33 | s51 |
| 23 | s52 | s02 | s50 | s52 | s53 | s43 | s52 |
| 24 | s53 | s03 | s50 | s53 | s53 | s53 | s53 |
+----+-----+-----+-----+-----+-----+-----+-----+

Фаза №4 отрисовать граф состояний (Helicopter view)

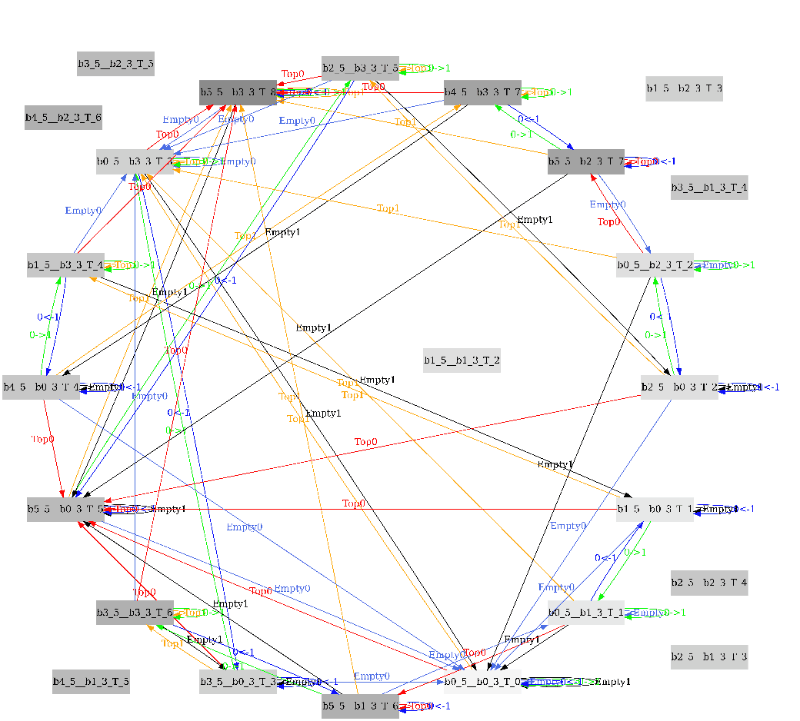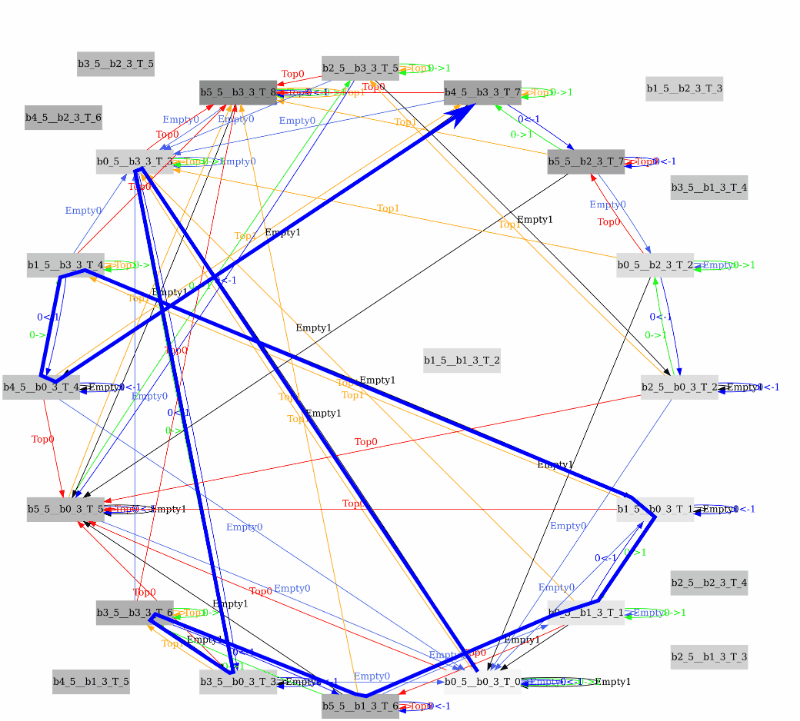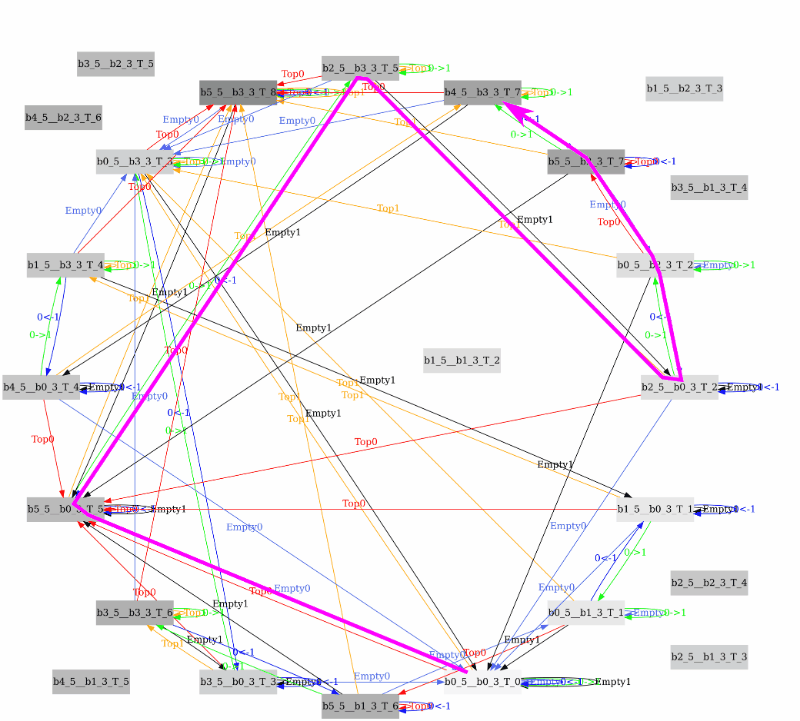
Как гласит английская народная пословица “Картинка стоит тысячи слов” (A picture is worth a thousand words). Также мой универский профессор часто говорил, что инженеры - это про схемы. Поэтому представляю блок-схему в виде ориентированного графа состояний для задачи про бутылки.

Я накропал на языке С консольную утилиту, которая прокручивает конечный автомат и сохраняет в файл составленный код на языке dot. Далее бесплатная утилита dot.exe поедает файл *.dot и преобразует его во всем известный *.svg файл. Наконец  браузер Chrome.exe поедает *.svg и отрисовывает в окне на мониторе. Язык Dot хорош тем что он имеет простой синтаксис. Dot более высокоуровневый язык, чем спецификация *.svg файлов.

Глядя на этот ориентированный граф становится очевидным, что чтобы отмерить 4 литра надо выполнить следующую  процедуру из 6-ти инструкций:

возможные действия с бутылками
возможные действия с бутылками

есть еще одно синее решение

Easy!
Вот код Dot графа для тех, кто захочет изучить граф внимательнее.

digraph G {
  b0_5__b0_3_T_0 [label="b0_5__b0_3_T_0" color=grey96 style=filled shape=box];
  b0_5__b0_3_T_0->b5_5__b0_3_T_5 [label="Top0" color=Red fontcolor=Red]
   b5_5__b0_3_T_5 [label="b5_5__b0_3_T_5" color=grey73 style=filled shape=box];
   b5_5__b0_3_T_5->b5_5__b0_3_T_5 [label="Top0" color=Red fontcolor=Red]
   b5_5__b0_3_T_5->b5_5__b3_3_T_8 [label="Top1" color=orange fontcolor=orange]
    b5_5__b3_3_T_8 [label="b5_5__b3_3_T_8" color=grey55 style=filled shape=box];
    b5_5__b3_3_T_8->b5_5__b3_3_T_8 [label="Top0" color=Red fontcolor=Red]
    b5_5__b3_3_T_8->b5_5__b3_3_T_8 [label="Top1" color=orange fontcolor=orange]
    b5_5__b3_3_T_8->b0_5__b3_3_T_3 [label="Empty0" color=royalblue fontcolor=royalblue]
    b0_5__b3_3_T_3 [label="b0_5__b3_3_T_3" color=grey82 style=filled shape=box];
    b0_5__b3_3_T_3->b5_5__b3_3_T_8 [label="Top0" color=Red fontcolor=Red]
    b0_5__b3_3_T_3->b0_5__b3_3_T_3 [label="Top1" color=orange fontcolor=orange]
    b0_5__b3_3_T_3->b0_5__b3_3_T_3 [label="Empty0" color=royalblue fontcolor=royalblue]
    b0_5__b3_3_T_3->b0_5__b0_3_T_0 [label="Empty1" color=aqua fontcolor=aqua]
    b0_5__b3_3_T_3->b0_5__b3_3_T_3 [label="0->1" color=green fontcolor=green]
    b0_5__b3_3_T_3->b3_5__b0_3_T_3 [label="0<-1" color=blue fontcolor=blue]
    b3_5__b0_3_T_3 [label="b3_5__b0_3_T_3" color=grey82 style=filled shape=box];
    b3_5__b0_3_T_3->b5_5__b0_3_T_5 [label="Top0" color=Red fontcolor=Red]
    b3_5__b0_3_T_3->b3_5__b3_3_T_6 [label="Top1" color=orange fontcolor=orange]
    b3_5__b3_3_T_6 [label="b3_5__b3_3_T_6" color=grey69 style=filled shape=box];
    b3_5__b3_3_T_6->b5_5__b3_3_T_8 [label="Top0" color=Red fontcolor=Red]
    b3_5__b3_3_T_6->b3_5__b3_3_T_6 [label="Top1" color=orange fontcolor=orange]
    b3_5__b3_3_T_6->b0_5__b3_3_T_3 [label="Empty0" color=royalblue fontcolor=royalblue]
    b3_5__b3_3_T_6->b3_5__b0_3_T_3 [label="Empty1" color=aqua fontcolor=aqua]
    b3_5__b3_3_T_6->b3_5__b3_3_T_6 [label="0->1" color=green fontcolor=green]
    b3_5__b3_3_T_6->b5_5__b1_3_T_6 [label="0<-1" color=blue fontcolor=blue]
    b5_5__b1_3_T_6 [label="b5_5__b1_3_T_6" color=grey69 style=filled shape=box];
    b5_5__b1_3_T_6->b5_5__b1_3_T_6 [label="Top0" color=Red fontcolor=Red]
    b5_5__b1_3_T_6->b5_5__b3_3_T_8 [label="Top1" color=orange fontcolor=orange]
    b5_5__b1_3_T_6->b0_5__b1_3_T_1 [label="Empty0" color=royalblue fontcolor=royalblue]
    b0_5__b1_3_T_1 [label="b0_5__b1_3_T_1" color=grey91 style=filled shape=box];
    b0_5__b1_3_T_1->b5_5__b1_3_T_6 [label="Top0" color=Red fontcolor=Red]
    b0_5__b1_3_T_1->b0_5__b3_3_T_3 [label="Top1" color=orange fontcolor=orange]
    b0_5__b1_3_T_1->b0_5__b1_3_T_1 [label="Empty0" color=royalblue fontcolor=royalblue]
    b0_5__b1_3_T_1->b0_5__b0_3_T_0 [label="Empty1" color=aqua fontcolor=aqua]
    b0_5__b1_3_T_1->b0_5__b1_3_T_1 [label="0->1" color=green fontcolor=green]
    b0_5__b1_3_T_1->b1_5__b0_3_T_1 [label="0<-1" color=blue fontcolor=blue]
    b1_5__b0_3_T_1 [label="b1_5__b0_3_T_1" color=grey91 style=filled shape=box];
    b1_5__b0_3_T_1->b5_5__b0_3_T_5 [label="Top0" color=Red fontcolor=Red]
    b1_5__b0_3_T_1->b1_5__b3_3_T_4 [label="Top1" color=orange fontcolor=orange]
    b1_5__b3_3_T_4 [label="b1_5__b3_3_T_4" color=grey78 style=filled shape=box];
    b1_5__b3_3_T_4->b5_5__b3_3_T_8 [label="Top0" color=Red fontcolor=Red]
    b1_5__b3_3_T_4->b1_5__b3_3_T_4 [label="Top1" color=orange fontcolor=orange]
    b1_5__b3_3_T_4->b0_5__b3_3_T_3 [label="Empty0" color=royalblue fontcolor=royalblue]
    b1_5__b3_3_T_4->b1_5__b0_3_T_1 [label="Empty1" color=aqua fontcolor=aqua]
    b1_5__b3_3_T_4->b1_5__b3_3_T_4 [label="0->1" color=green fontcolor=green]
    b1_5__b3_3_T_4->b4_5__b0_3_T_4 [label="0<-1" color=blue fontcolor=blue]
    b4_5__b0_3_T_4 [label="b4_5__b0_3_T_4" color=grey78 style=filled shape=box];
    b4_5__b0_3_T_4->b5_5__b0_3_T_5 [label="Top0" color=Red fontcolor=Red]
    b4_5__b0_3_T_4->b4_5__b3_3_T_7 [label="Top1" color=orange fontcolor=orange]
    b4_5__b3_3_T_7 [label="b4_5__b3_3_T_7" color=grey64 style=filled shape=box];
    b4_5__b3_3_T_7->b5_5__b3_3_T_8 [label="Top0" color=Red fontcolor=Red]
    b4_5__b3_3_T_7->b4_5__b3_3_T_7 [label="Top1" color=orange fontcolor=orange]
    b4_5__b3_3_T_7->b0_5__b3_3_T_3 [label="Empty0" color=royalblue fontcolor=royalblue]
    b4_5__b3_3_T_7->b4_5__b0_3_T_4 [label="Empty1" color=aqua fontcolor=aqua]
    b4_5__b3_3_T_7->b4_5__b3_3_T_7 [label="0->1" color=green fontcolor=green]
    b4_5__b3_3_T_7->b5_5__b2_3_T_7 [label="0<-1" color=blue fontcolor=blue]
    b5_5__b2_3_T_7 [label="b5_5__b2_3_T_7" color=grey64 style=filled shape=box];
    b5_5__b2_3_T_7->b5_5__b2_3_T_7 [label="Top0" color=Red fontcolor=Red]
    b5_5__b2_3_T_7->b5_5__b3_3_T_8 [label="Top1" color=orange fontcolor=orange]
    b5_5__b2_3_T_7->b0_5__b2_3_T_2 [label="Empty0" color=royalblue fontcolor=royalblue]
    b0_5__b2_3_T_2 [label="b0_5__b2_3_T_2" color=grey87 style=filled shape=box];
    b0_5__b2_3_T_2->b5_5__b2_3_T_7 [label="Top0" color=Red fontcolor=Red]
    b0_5__b2_3_T_2->b0_5__b3_3_T_3 [label="Top1" color=orange fontcolor=orange]
    b0_5__b2_3_T_2->b0_5__b2_3_T_2 [label="Empty0" color=royalblue fontcolor=royalblue]
    b0_5__b2_3_T_2->b0_5__b0_3_T_0 [label="Empty1" color=aqua fontcolor=aqua]
    b0_5__b2_3_T_2->b0_5__b2_3_T_2 [label="0->1" color=green fontcolor=green]
    b0_5__b2_3_T_2->b2_5__b0_3_T_2 [label="0<-1" color=blue fontcolor=blue]
    b2_5__b0_3_T_2 [label="b2_5__b0_3_T_2" color=grey87 style=filled shape=box];
    b2_5__b0_3_T_2->b5_5__b0_3_T_5 [label="Top0" color=Red fontcolor=Red]
    b2_5__b0_3_T_2->b2_5__b3_3_T_5 [label="Top1" color=orange fontcolor=orange]
    b2_5__b3_3_T_5 [label="b2_5__b3_3_T_5" color=grey73 style=filled shape=box];
    b2_5__b3_3_T_5->b5_5__b3_3_T_8 [label="Top0" color=Red fontcolor=Red]
    b2_5__b3_3_T_5->b2_5__b3_3_T_5 [label="Top1" color=orange fontcolor=orange]
    b2_5__b3_3_T_5->b0_5__b3_3_T_3 [label="Empty0" color=royalblue fontcolor=royalblue]
    b2_5__b3_3_T_5->b2_5__b0_3_T_2 [label="Empty1" color=aqua fontcolor=aqua]
    b2_5__b3_3_T_5->b2_5__b3_3_T_5 [label="0->1" color=green fontcolor=green]
    b2_5__b3_3_T_5->b5_5__b0_3_T_5 [label="0<-1" color=blue fontcolor=blue]
    b2_5__b0_3_T_2->b0_5__b0_3_T_0 [label="Empty0" color=royalblue fontcolor=royalblue]
    b2_5__b0_3_T_2->b2_5__b0_3_T_2 [label="Empty1" color=aqua fontcolor=aqua]
    b2_5__b0_3_T_2->b0_5__b2_3_T_2 [label="0->1" color=green fontcolor=green]
    b2_5__b0_3_T_2->b2_5__b0_3_T_2 [label="0<-1" color=blue fontcolor=blue]
    b5_5__b2_3_T_7->b5_5__b0_3_T_5 [label="Empty1" color=aqua fontcolor=aqua]
    b5_5__b2_3_T_7->b4_5__b3_3_T_7 [label="0->1" color=green fontcolor=green]
    b5_5__b2_3_T_7->b5_5__b2_3_T_7 [label="0<-1" color=blue fontcolor=blue]
    b4_5__b0_3_T_4->b0_5__b0_3_T_0 [label="Empty0" color=royalblue fontcolor=royalblue]
    b4_5__b0_3_T_4->b4_5__b0_3_T_4 [label="Empty1" color=aqua fontcolor=aqua]
    b4_5__b0_3_T_4->b1_5__b3_3_T_4 [label="0->1" color=green fontcolor=green]
    b4_5__b0_3_T_4->b4_5__b0_3_T_4 [label="0<-1" color=blue fontcolor=blue]
    b1_5__b0_3_T_1->b0_5__b0_3_T_0 [label="Empty0" color=royalblue fontcolor=royalblue]
    b1_5__b0_3_T_1->b1_5__b0_3_T_1 [label="Empty1" color=aqua fontcolor=aqua]
    b1_5__b0_3_T_1->b0_5__b1_3_T_1 [label="0->1" color=green fontcolor=green]
    b1_5__b0_3_T_1->b1_5__b0_3_T_1 [label="0<-1" color=blue fontcolor=blue]
    b5_5__b1_3_T_6->b5_5__b0_3_T_5 [label="Empty1" color=aqua fontcolor=aqua]
    b5_5__b1_3_T_6->b3_5__b3_3_T_6 [label="0->1" color=green fontcolor=green]
    b5_5__b1_3_T_6->b5_5__b1_3_T_6 [label="0<-1" color=blue fontcolor=blue]
    b3_5__b0_3_T_3->b0_5__b0_3_T_0 [label="Empty0" color=royalblue fontcolor=royalblue]
    b3_5__b0_3_T_3->b3_5__b0_3_T_3 [label="Empty1" color=aqua fontcolor=aqua]
    b3_5__b0_3_T_3->b0_5__b3_3_T_3 [label="0->1" color=green fontcolor=green]
    b3_5__b0_3_T_3->b3_5__b0_3_T_3 [label="0<-1" color=blue fontcolor=blue]
    b5_5__b3_3_T_8->b5_5__b0_3_T_5 [label="Empty1" color=aqua fontcolor=aqua]
    b5_5__b3_3_T_8->b5_5__b3_3_T_8 [label="0->1" color=green fontcolor=green]
    b5_5__b3_3_T_8->b5_5__b3_3_T_8 [label="0<-1" color=blue fontcolor=blue]
   b5_5__b0_3_T_5->b0_5__b0_3_T_0 [label="Empty0" color=royalblue fontcolor=royalblue]
   b5_5__b0_3_T_5->b5_5__b0_3_T_5 [label="Empty1" color=aqua fontcolor=aqua]
   b5_5__b0_3_T_5->b2_5__b3_3_T_5 [label="0->1" color=green fontcolor=green]
   b5_5__b0_3_T_5->b5_5__b0_3_T_5 [label="0<-1" color=blue fontcolor=blue]
  b0_5__b0_3_T_0->b0_5__b3_3_T_3 [label="Top1" color=orange fontcolor=orange]
  b0_5__b0_3_T_0->b0_5__b0_3_T_0 [label="Empty0" color=royalblue fontcolor=royalblue]
  b0_5__b0_3_T_0->b0_5__b0_3_T_0 [label="Empty1" color=aqua fontcolor=aqua]
  b0_5__b0_3_T_0->b0_5__b0_3_T_0 [label="0->1" color=green fontcolor=green]
  b0_5__b0_3_T_0->b0_5__b0_3_T_0 [label="0<-1" color=blue fontcolor=blue]
    b1_5__b1_3_T_2 [label="b1_5__b1_3_T_2" color=grey87 style=filled shape=box];
    b1_5__b2_3_T_3 [label="b1_5__b2_3_T_3" color=grey82 style=filled shape=box];
    b2_5__b1_3_T_3 [label="b2_5__b1_3_T_3" color=grey82 style=filled shape=box];
    b2_5__b2_3_T_4 [label="b2_5__b2_3_T_4" color=grey78 style=filled shape=box];
    b3_5__b1_3_T_4 [label="b3_5__b1_3_T_4" color=grey78 style=filled shape=box];
    b3_5__b2_3_T_5 [label="b3_5__b2_3_T_5" color=grey73 style=filled shape=box];
    b4_5__b1_3_T_5 [label="b4_5__b1_3_T_5" color=grey73 style=filled shape=box];
    b4_5__b2_3_T_6 [label="b4_5__b2_3_T_6" color=grey69 style=filled shape=box];
}

Можно отрисовать граф на этом сайте и сохранить его в *.svg.

Graphviz Online
dreampuf.github.io

Редактировать *.svg можно при помощи бесплатной программы Inkscape.exe.

Эта задача может служить отличной иллюстрацией для обучения теории конечных автоматов FSM. Конечные автоматы повсеместно используются в промышленной разработке, например, системного программного обеспечения.

Существует 8 недостижимых состояний: 1/5_1/3; 1/5_2/3; 2/5_1/3; 2/5_2/3; 3/5_1/3; 3/5_2/3; 4/5_1/3; 4/5+2/3. В эти состояния никак не попасть как только не переливай содержимое сосудов. Если вы захотите завалить человека на собеседовании, то можно попросить его "как перелить жидкости так чтобы в каждой бутылине осталось по 2 литра?" или "как перелить жидкости так чтобы в каждой бутылке осталось по 1 литру?".

Формально можно отмерить не только 4 лита, а все значения от 1 до 8 включительно.

Вывод

Как видите, язык Front-End разметки Dot отлично подходит для автоматической отрисовки сложной векторной графики. Конечно dot тула несовершенна и даже планарные графы строит с пересечениями ребер. Если вы знаете тулу которая гарантирует планарность, то укажите это в комментариях.

Буду признателен, если пришлете описания подобного рода логических задач в комментариях к тексту.

Комментарии (29)


  1. vvviperrr
    23.04.2022 17:25
    #24292758
    +2

    никогда не понимал, как самуэль джексон так быстро ее решил в экстремальной ситуации. я сидел тупил минут 5.

    о, превью изменилось. ну теперь мой камент не имеет смысла. спасибо, автор.


    1. REPISOT
      23.04.2022 23:07
      #24293236
      +2

      Насчет экстремальной ситуации не скажу, но мне понадобилось секунд 15-20. Все дело в опыте. У нас такие задачи в школе постоянно давали. На две емкости, весы и монеты и прочее.


    1. tuxi
      23.04.2022 23:49
      #24293304
      +2

      Вот вам 2 канистры емкостью 5 и 3 литра, наполненные водой (то есть вода уже в канистрах и больше ее брать негде). Сделайте мне 2 раза по 4 литра)
      Казалось бы такая мелочь, а решение уже совсем другое (если вообще есть)

      Правильная постановка задачи, уже половина решения.


      1. LuchS-lynx
        24.04.2022 02:05
        #24293418
        +1

        формально если канистры симметричные, то, канистру наклонить и выливать воду пока она своей поверхностью не "рассечет" канистру по диагонали от одного края на днище до диаметрально противоположного края на верхнем срезе. Вернуть канистру в нормальное положение. то мы получим четко пол канистры. 5/2=2,5л, 3/2=1,5л, 2,5+1,5=4л, но такое решение упирается в симметрию формы


      1. Bronx
        24.04.2022 10:30
        #24293732
        +2

        если вообще есть

        Я так полагаю, что есть ещё какая-то пустая безразмерная ёмкость, в которую нужно будет отлить вторые 4 литра? Тогда


        <3, 5, 0> : [1->3] : 
<0, 5, 3> : [2->1] : 
<3, 2, 3> : [1->3] : 
<0, 2, 6> : [2->1] : 
<2, 0, 6> : [3->2] : 
<2, 5, 1> : [2->1] : 
<3, 4, 1> : [1->3] : <0, 4, 4>

        где <...> — векторы состояния (объём воды в емкостях 1, 2 и 3),
        и [x->y] — переходы "перелить из x в y сколько можно"


        Пустая ёмкость должна вмещать больше 6 литров (если ровно 6, то решение можно укоротить на один шаг)


        1. Bronx
          25.04.2022 00:09
          #24294840

          Но, вообще говоря, это то же самое решение, что и для исходной задачи, просто внешняя среда заменена на специальную ёмкость, и шаги типа "вылить всю воду в окружающее пространство" заменены на "вылить всю воду в ёмкость 3"


    1. Enverest
      24.04.2022 10:52
      #24293756

      Превью не изменилось. КПДВ видно в списке статей, а внутри поста картинки нету. Boomburum — это баг или так задумано?


      1. Dolios
        24.04.2022 11:26
        #24293782
        +1

        Сейчас превью и статья, насколько я знаю, это просто разные тексты. Кто-то там одно и то же размещает, кто-то нет.


  1. vesper-bot
    23.04.2022 17:50
    #24292794
    +4

    не далее как пару недель назад я пытался написать именно общее (N ведер, X1...XN объемы, вектор начального состояния, вектор целевого состояния) решение задачи с ведрами на Прологе. Не осилил, хотя технически ничего сверхсложного, вроде бы.


    А ещё — я не вижу в этой статье вообще ничего содержательного про dot. Только "породил текст прогой на С, скормил его проге на dot, получил SVG". Мало! Как минимум нужно описать, почему вообще dot, а не какая-нибудь утилита для генерации SVG.


    1. kenoma
      23.04.2022 21:52
      #24293118
      +1

      dot поразительно похож на популярные языки разметки uml типа Mermaid или PlantUML, никогда не ощущал особых проблем при переходе между ними. Ценность dot разве что в том, что рендеринг графа может быть осуществлен с помощью разных средств визуализации и что сам dot может рендерить громадные графы. Правда, ценность последнего сомнительна.


  1. Asparagales
    23.04.2022 19:00
    #24292892
    +2

    Взять и налить в 5-литровую емкость 5л. жидкости, а затем из нее наполнить 3-литровую емкость. В первой емкости останется два литра. Выливаете жидкость из обоих емкостей и повторяете процесс. Так мы отмеряли 4 л. В условиях задачи не сказано, что эти литры должны быть в этих емкостях, а не на полу, так что все правильно. Если что, ответить вам скоро не смогу из-за кармы. Нет, доту мы не знаем, мы и так эти задачки щелкаем за минуту.


    1. screwer
      23.04.2022 19:04
      #24292896
      +4

      В крепком орешке именно что сказано - надо было поставить на весы 4кн чтобв отключить бомбу.


    1. Alexashka
      23.04.2022 23:05
      #24293230
      +8

      Вылить 3л в 5л первый раз, во второй раз в трехлитровой останется 1 литр. Опорожнить пятилитровую. Вылить в нее литр из трешки и налить еще одну трешку.


      1. ramiil
        23.04.2022 23:12
        #24293252
        +7

        Налить в пятилитровку. Перелить в трёхлитровку. В пятилитровке останется два, вылить на землю из трёхлитровки, налить из пятилитровки оставшиеся два литра в трёшку и снова наполнить пятилитровку. Отлить из пятилитровки в трёхлитровку литр воды. В пятилитровке останется ровно четыре литра.


      1. xaosxaos2
        24.04.2022 10:13
        #24293716

        А если вот так, у вас только две канистры 5л и 3л, наполненные водой, доп. ёмкостей нет, воды другой нет.


        1. randomsimplenumber
          24.04.2022 16:36
          #24294186

          Не всякая задача имеет решение.


          1. MikeLP
            24.04.2022 20:44
            #24294502

            Можно половину 5 литров слить и половину 3 литров слить. :)


            1. randomsimplenumber
              24.04.2022 21:35
              #24294608

              Хорошо тому живётся, кто в уме умеет считать интеграл по объему и у кого глаз-ватерпас ;)


            1. Alexandroppolus
              26.04.2022 02:10
              #24297906

              Половину можно вылить, например, из цилиндрической ёмкости, но в условии ни слова о форме..

              Кстати, вспомнилась не совсем стандартная задачка на переливания


  1. edo1h
    23.04.2022 19:56
    #24292958
    +7

    язык программирования? серьёзно?


  1. Rsa97
    23.04.2022 20:35
    #24293002

    Этот пункт я пропущу так как таблица получится циклопических размеров. По правилу умножения 24*5=120 строк
    Таблица получится ровно на 24 строки. Каждая строка содержит все переходы из одного состояния, а состояний у вас 24.


    1. Tyusha
      23.04.2022 22:14
      #24293148
      +1

      Я так понимаю для состояния возможны действия: наполнить из источника 5, наполнить изисточника 3, слить 5, слить 3, перелить 5 в 3, перелить 3 в 5. Но для некоторых состояний не всё действия возможны, например, когда сосуд пуст, сливать его бессмысленное, нового состояния не возникнет.


      1. Rsa97
        24.04.2022 00:46
        #24293366
        +3

        Это неважно. Таблица задаёт переходы из состояния в состояние под действием входных символов. Поскольку у нас 24 состояния, то в таблице будет 24 строки. Поскольку у нас 6 входных символов, то в таблице будет 6 колонок переходов плюс колонка исходного состояния.
        Обозначим состояния через sXY, где X — количество воды в 5-литровой бутыли, Y — количество воды в 3-литровой. Входные символы (действия) обозначим как E5 — опустошить 5-литровую бутыль, E3 — опустошить 3-литровую, F5 — заполнить 5-литровую, F3 — заполнить трёхлитровую, 5T3 — перелить из 5-литровой в 3-литровую, 3T5 — из 5-литровой в 3-литровую бутыль.
        Тогда таблица переходов будет выглядеть так:

        +-----+-----+-----+-----+-----+-----+-----+
|     |  E5 |  E3 |  F5 |  F3 | 5T3 | 3T5 |
+-----+-----+-----+-----+-----+-----+-----+
| s00 | s00 | s00 | s50 | s03 | s00 | s00 |
| s01 | s01 | s00 | s51 | s03 | s01 | s10 |
| s02 | s02 | s00 | s52 | s03 | s02 | s20 |
| s03 | s03 | s00 | s53 | s03 | s03 | s30 |
| s10 | s00 | s10 | s50 | s13 | s01 | s10 |
| s11 | s01 | s10 | s51 | s13 | s02 | s20 |
| s12 | s02 | s10 | s52 | s13 | s03 | s30 |
| s13 | s03 | s10 | s53 | s13 | s13 | s40 |
| s20 | s00 | s20 | s50 | s23 | s02 | s20 |
| s21 | s01 | s20 | s51 | s23 | s03 | s30 |
| s22 | s02 | s20 | s52 | s23 | s13 | s40 |
| s23 | s03 | s20 | s53 | s23 | s23 | s50 |
| s30 | s00 | s30 | s50 | s33 | s03 | s30 |
| s31 | s01 | s30 | s51 | s33 | s13 | s40 |
| s32 | s02 | s30 | s52 | s33 | s23 | s50 |
| s33 | s03 | s30 | s53 | s33 | s33 | s51 |
| s40 | s00 | s40 | s50 | s43 | s13 | s40 |
| s41 | s01 | s40 | s51 | s43 | s23 | s50 |
| s42 | s02 | s40 | s52 | s43 | s33 | s51 |
| s43 | s03 | s40 | s53 | s43 | s43 | s52 |
| s50 | s00 | s50 | s50 | s53 | s23 | s50 |
| s51 | s01 | s50 | s51 | s53 | s33 | s51 |
| s52 | s02 | s50 | s52 | s53 | s43 | s52 |
| s53 | s03 | s50 | s53 | s53 | s53 | s53 |
+-----+-----+-----+-----+-----+-----+-----+

        И откуда тут взять 120 строк?


  1. Survtur
    23.04.2022 20:49
    #24293024
    +3

    Ой, я видел шикарное видео на канале mathologer - наглядное решение этой задачи в графичечком виде.

    https://youtu.be/0Oef3MHYEC0


  1. VT100
    23.04.2022 20:57
    #24293040
    +1

    А нет ли у Вас чего-то вроде IAR Visual State(?), чтобы по псевдокоду Dot получить исходник на C? Будет разом и алгоритм и исходник.


  1. mentin
    24.04.2022 03:06
    #24293460
    +1

    Dot хорош что отличная инфраструктура для разработчиков, на любой платформе. Ну и то что ему лет 50 наверное и всё давно отполировано и исправлено.

    Из свежего, для рисования диаграмм популярен Mermaid, его можно скажем вставлять в .md файлы на GitHub.


  1. KaminskyIlya
    24.04.2022 09:47
    #24293670
    +2

    Такого рода задачи легко решаются при помощи теории групп. Мало того, именно при помощи теории групп вы сможете доказать, что задача вообще имеет решение. Числа 5 и 3 взаимно просты, а значит вы легко сможете получить любое значение: 1, 2, 3, 4, 5 литров. А вот для комбинации 6, 3 получить 2 литра уже не получится. Попробуйте доказать это или опровергнуть самостоятельно.

    И не нужно строить никаких гигантских таблиц и конечных автоматов. Яркий пример, когда знания математики программистам нужны.


  1. BubaVV
    24.04.2022 11:33
    #24293796

    Можно решить через треугольную диаграмму. Сумма высот от любой точки треугольника постоянна, все достижимые переливанием состояния лежат на краю диаграммы. Ну и ограничения по объемам легко добавить, срезав вершину

    https://www.cut-the-knot.org/triangle/glasses.shtml


  1. gdt
    24.04.2022 13:37
    #24293964

    Мы в университете решали на прологе/хаскелле через поиск (bfs/dfs) в пространстве состояний - примерно как у вас только таблица переходов нигде не хранится, а переходы из одного состояния в другой задаются как раз допустимыми действиями. Там и литры и волки с козлами и капустой и т д - все решается примерно по одинаковой методике и одинаково легко. Жаль с шахматами такое уже не прокатывает.