Math first / forpes.ru

24.06.2022 08:58

demsp 0 57 Источник

Данная статья посвящена, в основном, дробям (цепным дробям) и приближениям к иррациональным числам (в частности, приближениям к золотому сечению). Попутно затрагиваются вопросы, связанные с решением квадратных уравнений и построению "золотых" фигур.

Рассмотрим алгоритмическое решение задачи №38 из книги "Задачи для детей от 5 до 15 лет"

Вычислить сумму:

$\frac{ 1 }{ 1\cdot2 } + \frac{ 1 }{ 2\cdot3 } + \frac{ 1 }{ 3\cdot4 } + ... + \frac{ 1 }{ 99\cdot100 }$

Ниже представлен алгоритм для вычисления частичных сумм этого ряда на языке Scheme Lisp в среде drRacket (Scheme позволяет производить вычисления в обыкновенных дробях):

#lang racket 
(define series_sum  ( lambda (n)   (if (= n 0) 0      
  (+ (/ 1 (* n (+ n 1))) (series_sum(- n 1)))   ) ) ) 
  (series_sum 10) 
  (series_sum 100) 
  (series_sum 1000) 
  (series_sum 10000) 
  (series_sum 100000) 
  (series_sum 1000000)

Два последних примера drRacket вычислил с ошибкой

Эту программу можно запустить в online ide ideone.com и codepad.org.

Решение представлено как в обыкновенных, так и в периодических десятичных дробях. Кстати, чтобы перевести периодическую десятичную дробь в обыкновенную, необходимо данную дробь принять за

Далее необходимо данное равенство умножить на $10^{n}$ , где равняется периоду десятичной дроби и вычесть из данного равенства предыдущее

$99x=90 \leftrightarrow\ x=\frac{90}{99}=\frac{10}{11}$

Этот же алгоритм на Python

Ссылка на ideone.com

 def series_sum(n):     
    if n==0:         
      return 0     
    else:         
      return 1.0/(n*(n+1.0))+series_sum(n-1.0)   
print(series_sum(10)) 
print(series_sum(100))

Если рассмотреть частичные суммы в обыкновенных дробях, то можно заметить, что сумма ряда равна

$\frac{ n }{ n + 1 }$

Напомню, что

$\lim \frac{ n }{ n+1 } = \frac{ 1 }{ 1+ \frac{1}{n} } = \frac{1}{1}=1\; при \; n\to\infty$

Решение, использующее теорему Штольца

$\lim\frac{n}{n+1}=\lim\frac{(n+1)-n}{(n+2)-(n+1)}=\lim\frac{n-n+1}{n-n+2-1}=\frac{1}{1}=1$

Эту задачу можно встретить в различных книгах, посвященных математической индукции.

1.При гипотеза верна, так как $S_{1}=\frac{1}{2}$

2.Предположим, что гипотеза верна и для n=k, т.е. что

$S_{k}= \frac{ 1 }{ 1\cdot2 } + \frac{1}{2\cdot3}+...+\frac{1}{k(k+1)}=\frac{k}{k+1}$

где - некоторое натуральное число. Установим справедливость и при

$S_{k+1}= \frac{ k+1 }{ k+2 }$

$S_{k+1}=S_{k} + \frac{ 1 }{ (k+1)(k+2) } = \frac{k}{k+1} + \frac{1}{(k+1)(k+2)}=$ $=\frac{k^{2}+2k+1}{(k+1)(k+2)}=\frac{k+1}{k+2}$

Общий случай

Во втором томе "Курса дифференциального и интегрального исчисления" 363.4 рассматривается общий случай

$\sum \frac{ 1 }{ ( \alpha + n)( \alpha + n +1) } = \frac{ 1 }{ \alpha + 1 }$

Рассмотрим ещё один пример из задачника

43. Числа кроликов "Фибоначчи", образуют последовательность

$(a_{1}=1), 1, 3, 5, 8, 13, 21, 34, ...,$

в которой $a_{n+2}=a_{n+1}+a_{n}$ для всякого n = 1, 2, ... Найти наибольший общий делитель чисел $a_{100}$ и $a_{99}$ .

Ответ: Два соседних числа Фибоначчи взаимно просты, т.е. $НОД(u_{n+1},u_{n})=1$

НОД-это Наибольший Общий Делитель.

"Доказательство из книги "За страницами учебника математики" 10-11

Из равенства $u_{n+2} = u_{n+1} + u_{n}$ следует, что $НОД(u_{n+2},u_{n+1}) = НОД(u_{n+1},u_{n})$ . Пятясь таким образом назад, придём к $НОД(u_{2},u_{1}) = НОД(1,1) = 1$ , а потому два соседних числа Фибоначчи взаимно просты.

Поясню, что $НОД(u_{n+2},u_{n+1}) = НОД(u_{n+1},u_{n})$ по алгоритму Евклида, поскольку $НОД(u_{n+2},u_{n+1}) = НОД(u_{n+1},r)$ где - остаток от деления $u_{n+2}$ на $u_{n+1}$ , то в данном конкретном случае $r = u_{n}$ поскольку $u_{n+2} = u_{n+1} + u_{n}$

Кстати, по теореме Гаусса: "если число является НОД двух чисел и , то справедливо равенство , где и являются целыми числами"

Если вместо чисел и подставить соседние числа Фибоначчи, то получим тождество Кассини

$F_{n-1}F_{n+1}-F_{n}^2=(-1)^n$

Нетрудно заметить, что числа и тоже удовлетворяют условию взаимной простоты.

Эту теорему можно применить для решения задачи об алхимике и свечах из статьи "История поиска длиной в 15 лет" по ссылке

###

Приближения к золотому сечению

В следующей задаче необходимо вычислить золотое сечение, $\frac{\sqrt{5}+1}{2}\approx 1,618$

Это соотношение сторон открытки, остающейся себе подобной при отрезании квадрата, стороной которого является меньшая сторона открытки. Обычно обозначается прописной греческой буквой $\Phi$ (фи), в честь древнегреческого скульптора и архитектора Фидия, реже — греческой буквой $\tau$ (тау).

53. Для последовательности чисел Фибоначчи $a_{n}$ задачи 43 найти предел отношения

$\frac { a_{n+1} }{ a_{n} }$ при стремлении к бесконечности:

$\frac { a_{n+1} }{ a_{n} } = 2, \frac {3}{2}, \frac {5}{3}, \frac {8}{5}, \frac {13}{8},\frac {21}{13}, \frac {34}{21}$

Рассмотрим отрезки, представляющие собой разности двух соседних членов ряда $\frac{a_{n+1}}{a_{n}}$

Четные члены ряда $\frac { a_{n+1} }{ a_{n} }$ представляют растущую последовательность $x_{n}$

$\frac{ 3 }{ 2 }, \frac{ 8 }{ 5 }, \frac{ 21 }{ 13 }, ...,$

Нечетные члены ряда $\frac { a_{n+1} }{ a_{n} }$ представляют убывающую последовательность $y_{n}$

$2 , \frac{ 5 }{ 3 }, \frac{ 13 }{ 8 }, ...,$

По лемме о вложенных промежутках "Курс дифференциального и интегрального исчисления"

$c = \lim x_{n} = \lim y_{n}$

Для нашего ряда в точке справедливо равенство $\frac { a_{n+2} }{ a_{n+1} } = \frac { a_{n+1} }{ a_{n} }$

Разделив $a_{n+2} = a_{n+1} + a_{n}$ на $a_{n+1}$ , получим уравнение $\frac{a_{n+2}}{a_{n+1}} = 1 + \frac{a_{n}}{a_{n+1}}$

Произведя замену $\frac{a_{n+2}}{a_{n+1}}=x , \frac{a_{n}}{a_{n+1}} = \frac{1}{x}$ получим квадратное уравнение

$x = 1 + \frac{1}{x} \leftrightarrow x^2=x+1 \leftrightarrow x^2-x-1$

Решение этого уравнения рассматривается в конце статьи.

Если в программе geogebra соединить дугами окружности точки 2 и $\frac{3}{2}$ , $\frac{3}{2}$ и $\frac{5}{3}$ , $\frac{5}{3}$ и $\frac{8}{5}$ и т.д. - получим самоподобную фигуру

Для сравнения

Вообще, существует стандартный алгоритм вычисления чисел Фибоначчи на Python. Этот алгоритм представлен на сайте Python.org

def fib(n):
	    a, b = 0, 1
	    while a < n:
		print(a)
		a, b = b, a+b
fib(100)

Изменим данный алгоритм так, чтобы он выводил на печать приближения к золотому сечению. Для двух соседних чисел a и b будем сумму a+b делить на b

def fib(n):
	    a, b = 0.0 , 1.0
	    while a < n:
		print((a+b)/b)
		a, b = b, a+b
fib(100)

На двенадцатом шаге получим приближение, равное 1.61805 Проверить можно по ссылке

А само золотое сечение можно использовать для вычисления n-ого числа Фибоначчи.

Формула Бине выражает в явном виде значение Fn как функцию от n:

$F_{n}=\frac{(\frac{1+\sqrt{5}}{2})^n-(\frac{1-\sqrt{5}}{2})^n}{\sqrt{5}}$

Сразу можно заметить, что второе слагаемое всегда меньше единицы при любом целом неотрицательном . Поэтому, зная, что формула Бине даёт целые числа, можно утверждать, что

$F_{n}=[\frac{(\frac{1+\sqrt{5}}{2})^n}{\sqrt{5}}]$

где квадратные скобки [...] обозначают округление заключенного в них числа до ближайшего целого.

А из этого следует, что для соседних чисел Фибоначчи справедливо равенство

$F_{n+1}=[F_n \cdot \Phi ]$

В первом томе монографии Дональда Кнута "Искусство программирования" есть задача, использующая это соотношение:

Вычислить, чему равно $F_{n+1}-F_n \cdot \Phi$

На Хабре есть статья, где рассматриваются 5 способов вычисления чисел Фибоначчи, в том числе формула Бине.

Далее, если в уравнении $x = 1 + \frac{1}{x}$ в правой части заменить x на $1 + \frac{1}{x}$ то получим

$x = 1 + \frac{1}{1 + \frac{1}{x}}$

Продолжая производить замены, придём к представлению золотого сечения в виде цепной дроби

$1+ \frac{1}{1 + \frac{1}{1+ \frac{1}{1+ \frac{1}{1+ \frac{1}{1+...}}}}}$

Ниже представлен алгоритм Python для вычисления приближений к золотому сечению, использующий эту форму (форму бесконечной цепной дроби)

arr=[1.0]
def foo(a):
	b=1.0+1.0/(1.0+1.0/a[len(a)-1])
	return b
arr.append(foo(arr)) #первый шаг
arr.append(foo(arr)) #второй шаг
arr.append(foo(arr)) #третий шаг
print (arr)

На десятом шаге получим приближение, равное 1.618033985

В книге «Задачи для детей от 5 до 15 лет» есть похожий пример 54. Вычислить бесконечную цепную дробь

$1+ \frac{1}{2 + \frac{1}{1+ \frac{1}{2+ \frac{1}{1+ \frac{1}{2+...}}}}}$

Решение. Рассмотрим уравнение $\alpha = 1+ \frac{1}{2 + \frac{1}{ \alpha}}$

Согласно теоремам 236 и 235 из книги "Теория чисел":

$\alpha = \frac{ P_{1}\alpha+ P_{0}}{Q_{1}\alpha+ Q_{0} }$

Составляем таблицу значений $P_{n}$ и $Q_{n}$ при

	1	2
P	1	3
Q	1	2

так что $\alpha = \frac{ 3\alpha + 1 }{ 2\alpha + 1}, 2\alpha^{2} - 2\alpha -1 = 0$

и поскольку $\alpha > 0 ,$ то $\alpha = \frac{ 1 + \sqrt{3} }{ 2 }$

Золотое сечение может быть представлено в виде бесконечно вложенных радикалов

В некоторых случаях бесконечно вложенные радикалы могут быть тождественны некоторому рациональному числу, например выражение

$x=\sqrt{2+ \sqrt{2 +\sqrt{2 + ...} } }$ равно 2.

Для того, чтобы это увидеть, возведем обе части выражения в квадрат и отнимем число 2:

$x^{2}-2=\sqrt{2+ \sqrt{2 +\sqrt{2 + ...} } }=x \leftrightarrow x^{2}-x-2=0$

где $x_{1}=2;x_{2}=-1.$ Очевидно, что не может являться значением исходного радикала.

Вообще, $x=\sqrt{2 \sqrt{2\sqrt{2 ...} } }$ тоже равняется 2

>>> def foo(n,a):
... 	temp=a
... 	while(n>0):
... 		a=temp*(a**0.5)
... 		n=n-1
... 	return a**0.5
... 
>>> foo(50,2)
1.9999999999999993

Кстати, Рамануджан установил некоторые зависимости между бесконечно вложенными радикалами и рациональными числами

поскольку

$3=\sqrt{9}=\sqrt{1+2\cdot4}=\sqrt{1+2\sqrt{16}}$

$64=1+63=1+7\cdot9=...$

Золотое сечение можно представить в виде бесконечно вложенных радикалов таким образом:

Попробуйте самостоятельно установить справедливость данного тождества.

Данное выражение является частным случаем варианты $x_{n}=\sqrt{c+\sqrt{c+...+\sqrt{c}}}$

Курс дифференциального и интегрального исчисления, 35 (2):

"Таким образом $x_{n+1}$ получается из $x_{n}$ по формуле $x_{n+1} = \sqrt{c + x_{n} }$

...По основной теореме, варианта $x_{n}$ имеет некий конечный предел

Для определения его перейдём к пределу в равенстве

Мы получим, таким образом, что удовлетворяет квадратному уравнению $a^{2} = c + a$ Уравнение это имеет корни разных знаков; но интересующий нас предел не может быть отрицательным, следовательно, равен именно положительному корню:

$a=\frac{\sqrt{4c+1}+1}{2}"$

Значит "золотое сечение" является решением уравнения $a^{2} = c + a$ при

Далее в "Курсе дифференциального и интегрального исчисления" (353) рассматривается алгоритм вычисления обратного числа (такого числа 1/с, произведение которого на данное число с равно единице)

Пусть - любое положительное число, и положим $x_{n} = cy_{n}$ . Написанное выше рекуррентное соотношение заменится таким:

Взяв начальное значение $y_{0}$ под условием: $0<y_{0}<\frac{1}{c}$ , получим, что $y_{n}$ , монотонно возрастая, будет стремиться к $\frac{1}{c}.$

По этой схеме на счётных машинах и вычисляется число, обратное

.Ниже представлен алгоритм вычисления числа, обратного числу на языке Python:

( Ideone.com и codepad.org)

def reciprocal(c,y0,n):
	arr=[]
	for i in range(n):
		arr.append(y0)
		y0=y0*(2-c*y0)
        return arr

Функция reciprocal принимает на вход число , начальное значение $y_{0}$ , количество итераций и возвращает массив приближений к числу $\frac{1}{c}$

При $c<10\; y_{0}=0.1$

При $10<c<100\; y_{0}=0.01$

При $100<c<1000 \; y_{0}=0.001$

print reciprocal(3,0.1,5)
#[0.1, 0.17, 0.2533, 0.31411733000000003, 0.332225568981013]
print reciprocal(5,0.1,5)
#[0.1, 0.15000000000000002, 0.18750000000000003, 0.19921875000000003,0.19999694824218753]
print reciprocal(8,0.1,5) 
#[0.1, 0.12, 0.1248, 0.12499968, 0.1249999999991808]

Геометрическая интерпретация

Для приближенного вычисления обратного числа будем использовать метод касательных из книги "Digital Arithmetic".

Производной функции $y=\frac{1}{x}$ является $y'(x)=\frac{-1}{x^2}$

Касательными $y=f'(x_{0})(x-x_{0})+ f(x_{0})$ к гиперболе $y=\frac{1}{x}$ являются функции вида

$y=\frac{-1}{x_{0}^2}(x-x_{0})+\frac{1}{x_{0}}=\frac{-x+2x_{0}}{x_{0}^2}$ $y = \frac{2}{x_{0}} - \frac{x}{x_{0}^{2}}$

Вывод уравнения касательной

Уравнение прямой:

Уравнение прямой, проходящей через точку с координатами $(x_{0},y_{0}):$

$y_{0}=kx_{0}+b(II)$

Вычтем из уравнения (I) уравнение (II):

$y-y_{0}=kx-kx_{0}=\leftrightarrow y=k(x-x_{0})+f(x_{0})$

Так как угловой коэффициент касательной к графику дифференцируемой функции в точке с абсциссой $x_{0}$ равен $f'(x_{0})$ , то уравнение касательной принимает вид

$y=f'(x_{0})(x-x_{0})+f(x_{0})$

Подставляя числа вместо $x_{0}$ получим уравнения касательных

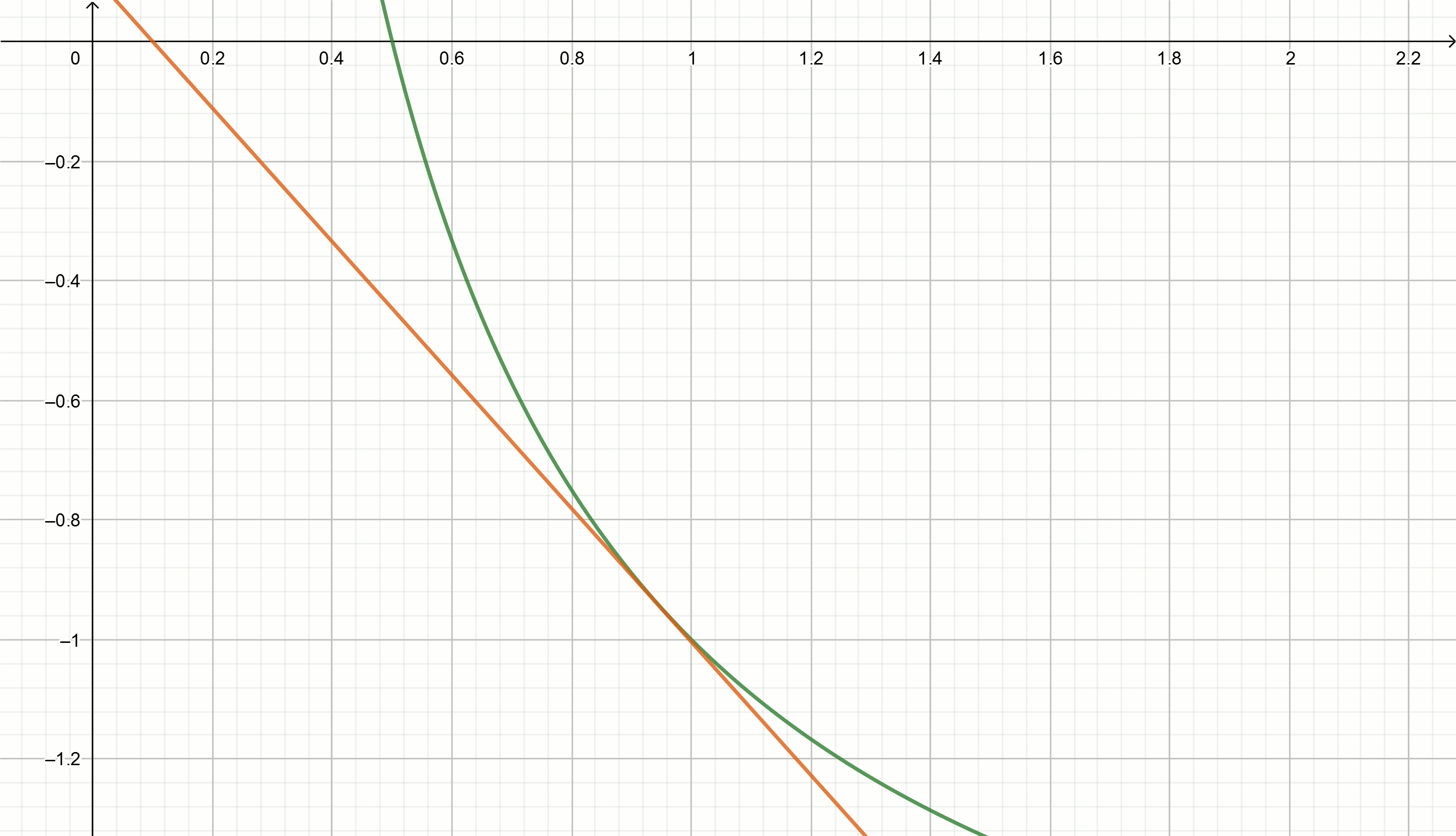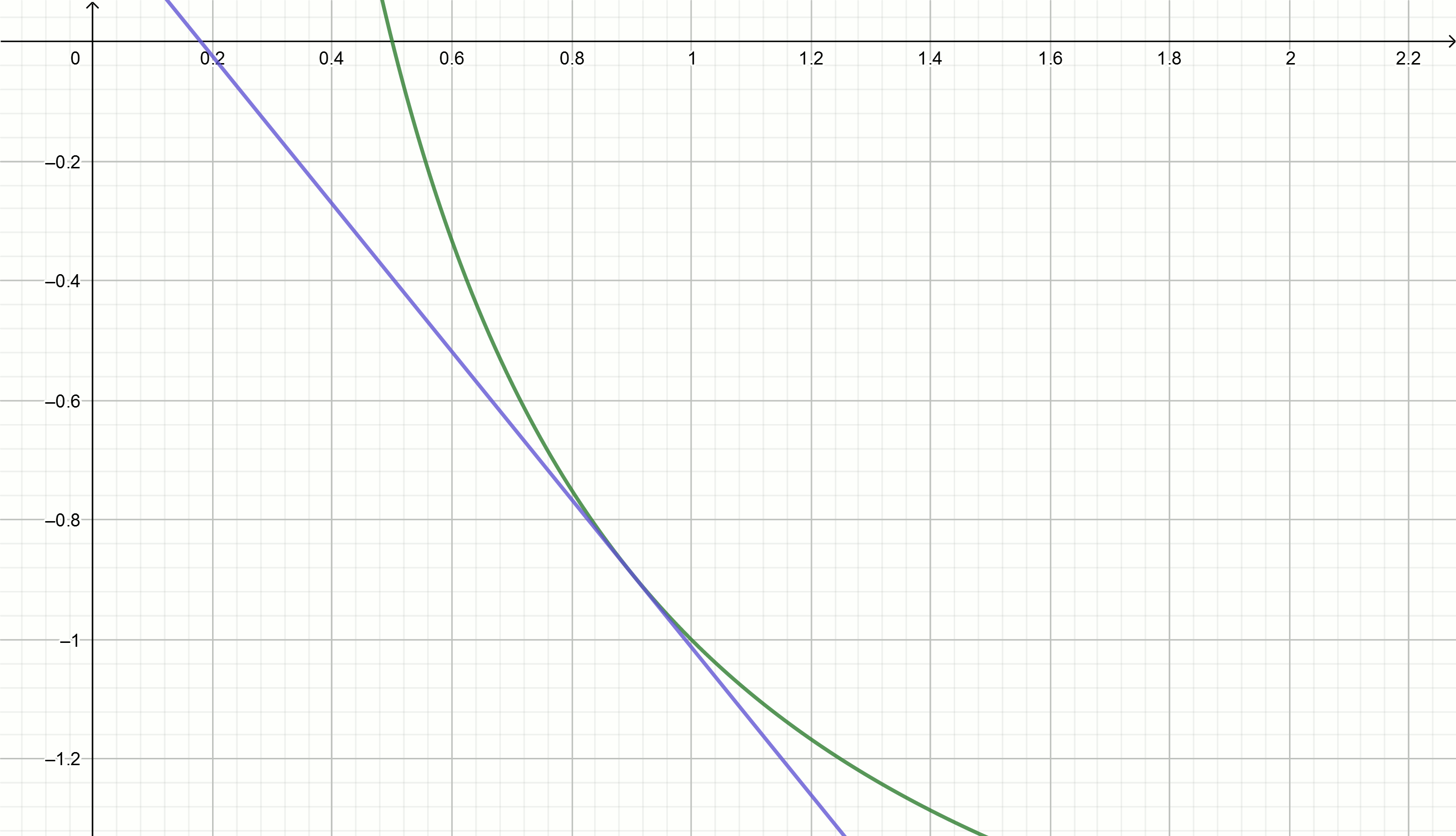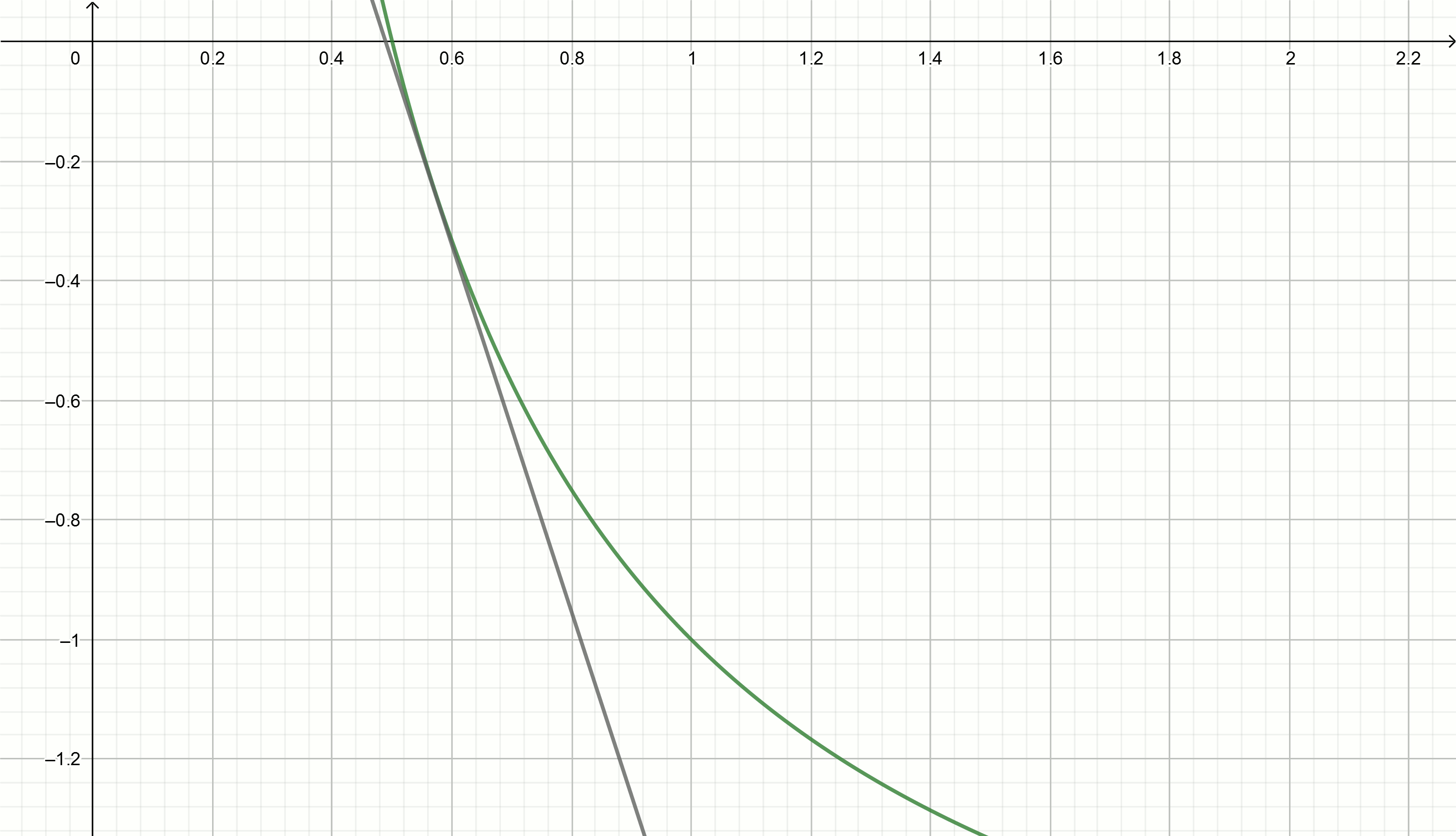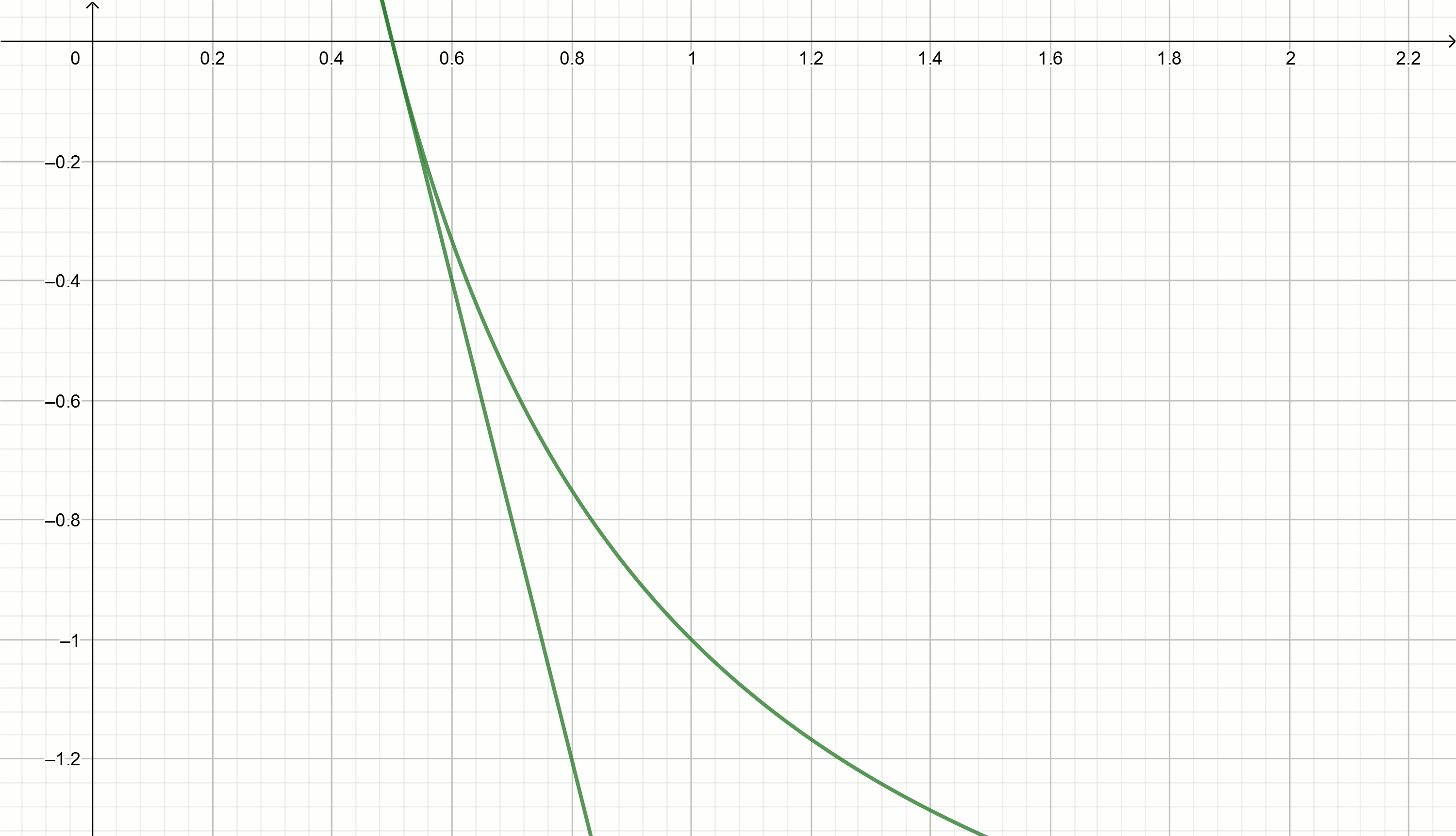
$y=2-x; \;\; y=1-\frac{x}{4}; \;\; y=\frac{2}{3}-\frac{x}{9}; \;\; y=\frac{1}{2}-\frac{x}{16}$

Построим эти графики

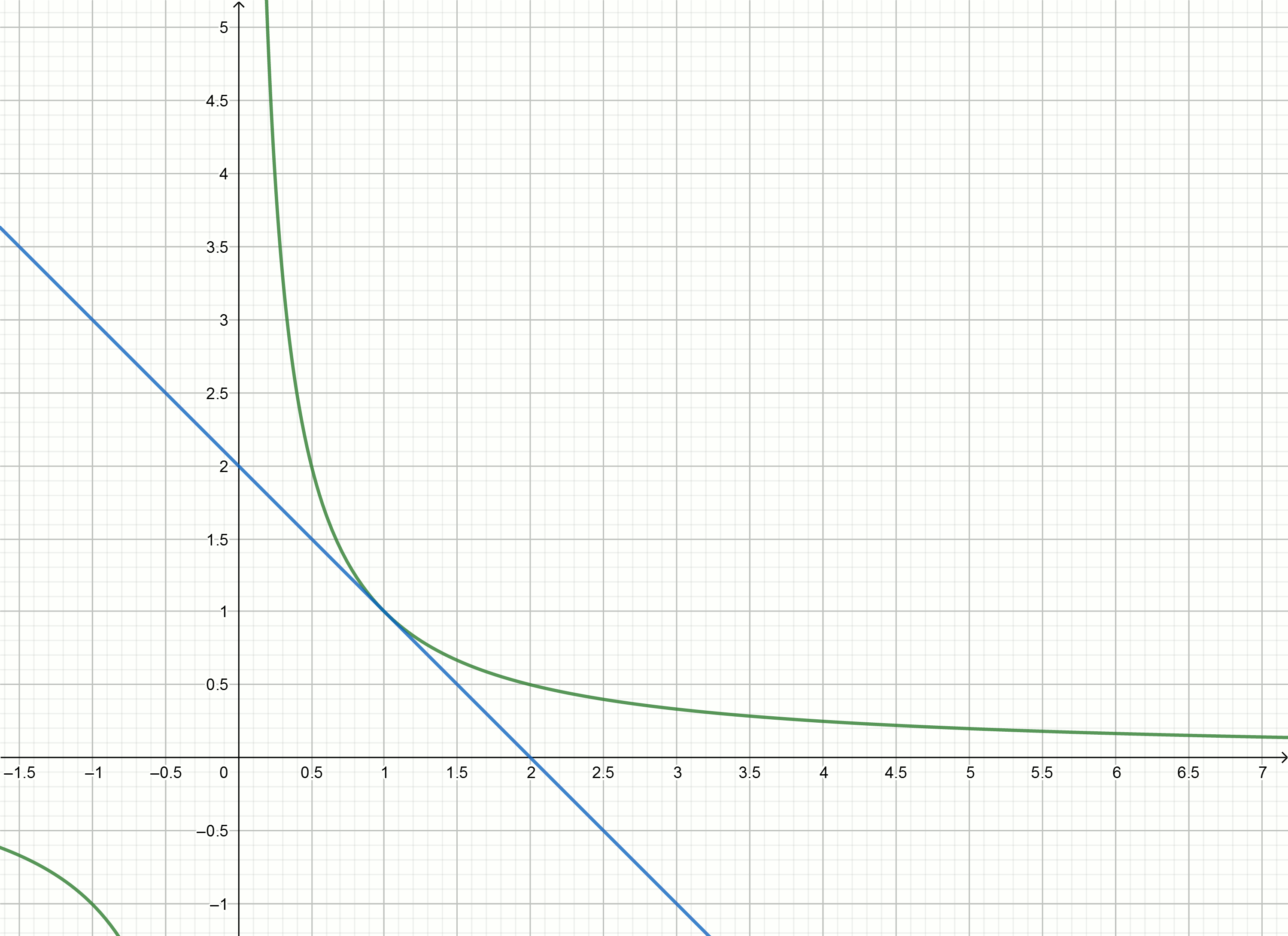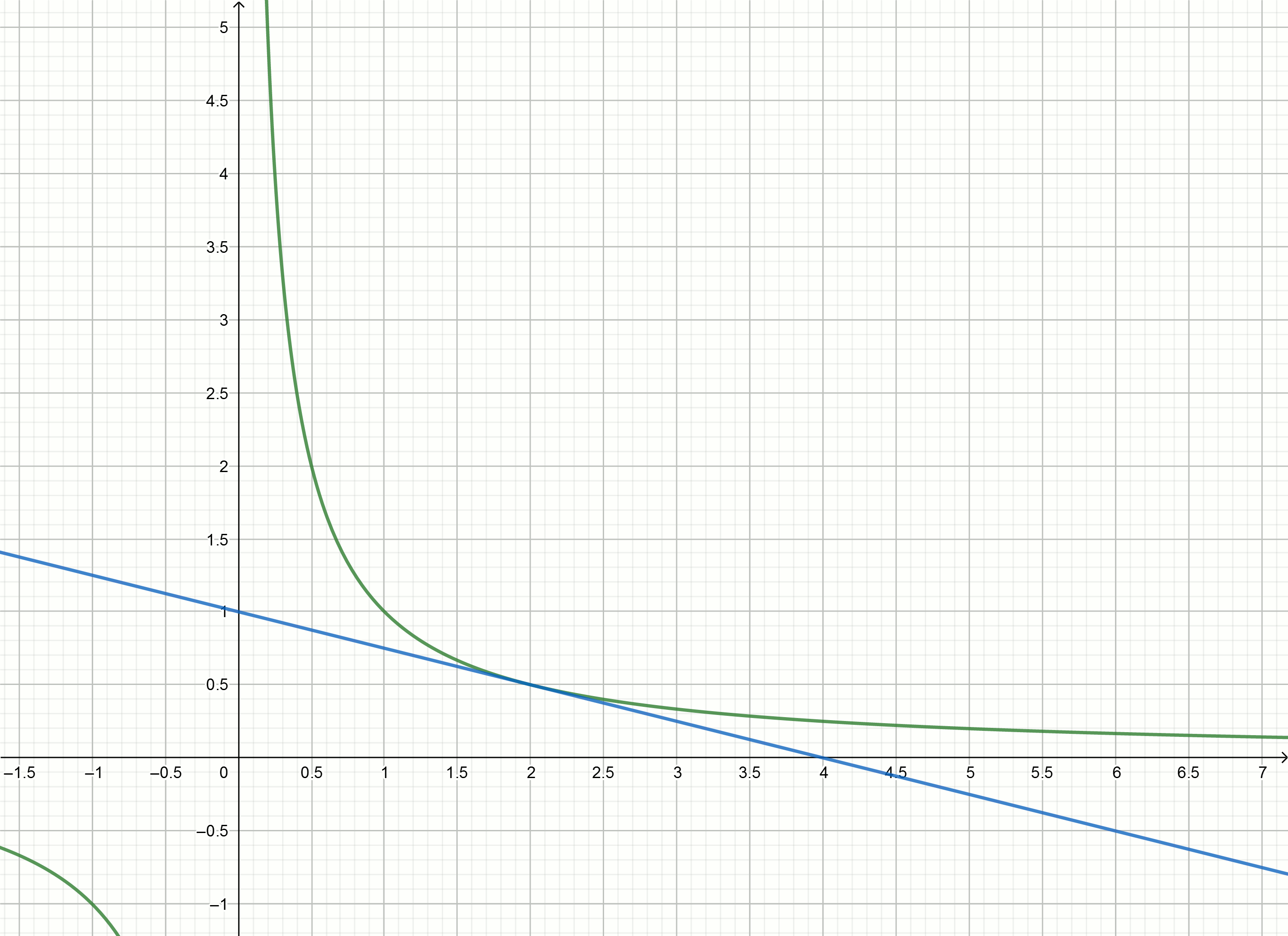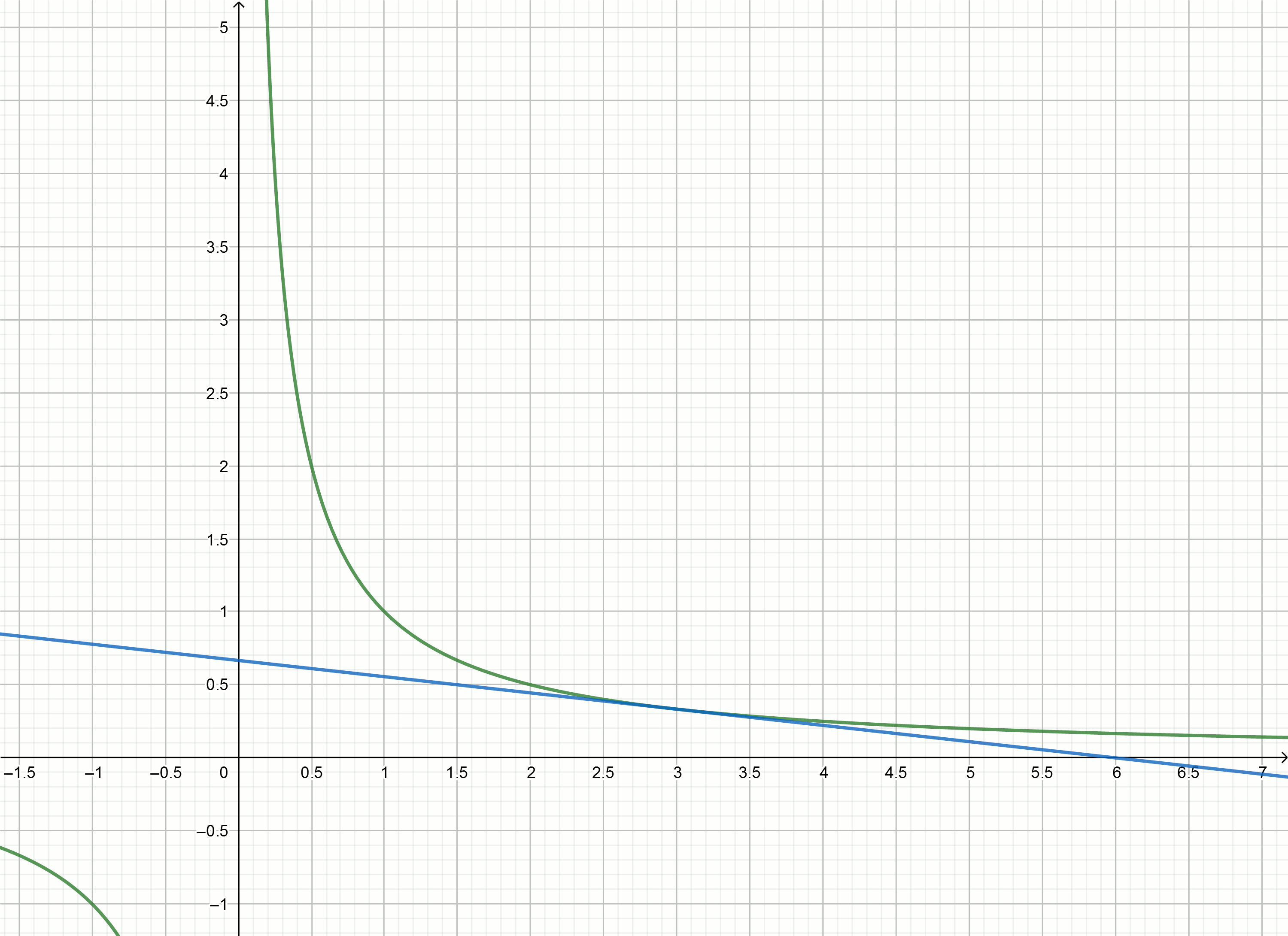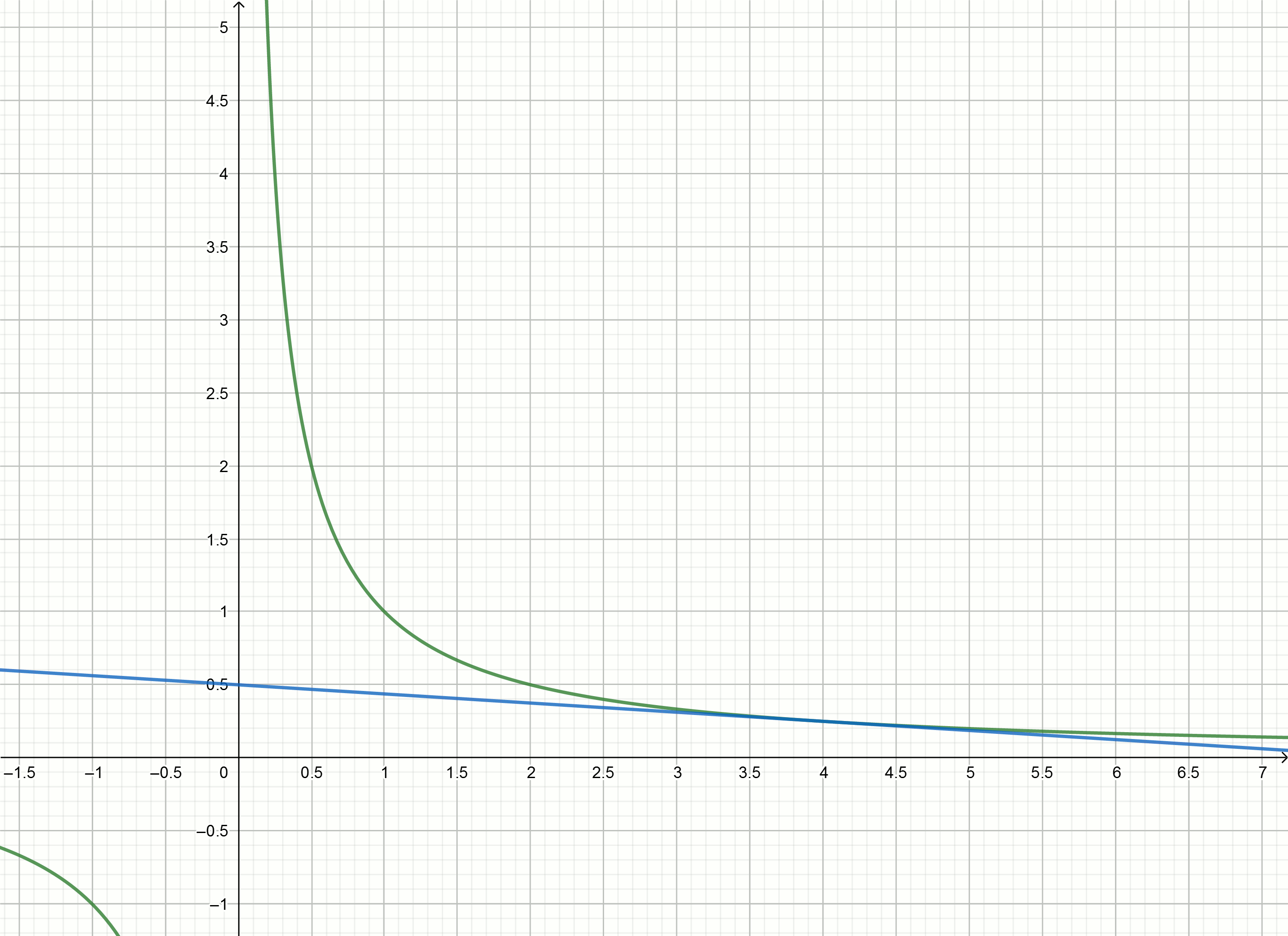
Если сдвинуть гиперболу вниз на $\alpha$ , то она пересечёт ось абсцисс в точке $\frac{1}{\alpha}$

Уравнение касательной преобразуется в $\frac{2}{x_{0}}-\frac{x}{x_{0}^2}-\alpha$

Далее, приравняв уравнение касательной к нулю и выразив , получим $x= x_{0} - \frac{f(x_{0})}{f'(x_{0})}$

Вместо $f(x_{0})$ подставим $\frac{1}{x_{0}} - \alpha$

Вместо $f'(x_{0})$ подставим $-\frac{1}{x_{0}^{2}}$

Получим выражение $x= x_{0} + (\frac{1}{x_{0}}-\alpha) x_{0}^{2}$

Раскрыв скобки, получим $x= x_{0} + x_{0}-\alpha x_{0}^{2} \rightarrow x=2x_{0}-\alpha x_{0}^2 \rightarrow x=x_{0}(2- \alpha x_{0})$

Подставим в уравнение $x=x_{0}(2-\alpha x_{0})$ и посмотрим, какие значения будет "пробегать"

При $\alpha=2$ получим (примерные значения)

Подставив эти значение в уравнение $y=\frac{2}{x_{0}}-\frac{x}{x_{0}^{2}}-2$

получим касательные, приближающиеся к

$y= 0.111 - \frac{x}{0.897} \;\; y= 0.222 - \frac{x}{0.81} \;\; y= 0.816 - \frac{x}{0.504} \;\; y= 0.857 - \frac{x}{0.49}\;\; y= 1.5 - \frac{x}{0.326} \;\; y= 2 - \frac{x}{0.25}$

Извлечение квадратного корня

Существует несколько методов для приближенного вычисления вычисления приближений квадратного корня из натурального числа.

Например алгоритм, использующий итерационный метод Герона $x_{n+1} = \frac{1}{2}x_{n}+\frac{a}{x_{n}}$ выглядит так

def square_root(a,n):        # a - подкоренное значение, n - количество циклов
        x0=1                      # первое приближение равно 1 
	arr=[]
	for i in range(n):
		arr.append(x0)       # добавляем к массиву новые приближения
		x0=0.5*(x0+a/x0)  # вычисляем приближения по формуле Герона
        return arr
print square_root(2,10)

codepad.org

Вычисление квадратного корня с помощью цепных дробей использовал Рафаэль Бомбелли

Чтобы найти значение $\sqrt{n}$ , сначала определим его целое приближение: $\sqrt {n}=a \pm r$ , где . Тогда $n=a\pm r^{2}=a^{2}\pm 2ar+r^{2}$ . Отсюда несложно вывести, что

$r={\frac {|n-a^{2}|}{2a\pm r}}$ .

Повторно подставляя полученное выражение в формулу $\sqrt {n}=a\pm r$ , мы получаем разложение в цепную дробь:

$a\pm {\frac {|n-a^{2}|}{2a\pm {\frac {|n-a^{2}|}{2a\pm {\frac {|n-a^{2}|}{2a\pm \cdots }}}}}}$

Значит можно записать алгоритм извлечения квадратного корня из натурального числа, используя разложение в цепную дробь

arr=[]
def square_root(n,a,n_count): # n-подкоренное значение, a - целая часть корня 
    x0=a                               # первое приближение равно a
    global arr
    for i in range(n_count): # результат будет больше искомой величины на a
        arr.append(x0-a)  # вычитаем a
        x0=2*a+(n-a*a)/x0
    
square_root(2.0,1.0,10) 
print(arr[9])
#Output: 1.4142139267767408

codepad.org

Для приближенного вычисления золотого сечения вычислим, чему равен $\sqrt{5}$ , прибавим к этому значению единицу и разделим получившееся число пополам

def square_root(n,a,n_count): # n-подкоренное значение, a - целая часть корня 
    x0=a                               # первое приближение равно a
    arr=[]
    for i in range(n_count): # результат будет больше искомой величины на a
        arr.append(x0-a)  # вычитаем a
        x0=2*a+(n-a*a)/x0
    return arr
 
print((square_root(5.0,1.0,10)[9]+1.0)/2.0)
#Output: 1.61842105263

ideone.com

Способ выделения целой части позволяет представить иррациональное число в виде бесконечной цепной дроби с единицами в числителях частыми числителями, равными единице. Вот пример разложения в цепную дробь числа $\sqrt{5}$ из книги "Алгебра"

$\sqrt{5}-2= \frac{\sqrt{5}-2\sqrt{5}+2}{\sqrt{5}+2}=\frac{1}{\sqrt{5}+2}$

Таким образом, $\sqrt{5} = 2+\frac{1}{\sqrt{5}+2}$

Выделим целую часть числа $\sqrt{5}+2:E\sqrt{5}+2=4$ . Значит, $\sqrt{5}+2$ можно представить в виде $4 + \alpha$ . Ясно, что $\alpha = \sqrt{5}+2-4=\sqrt{5}-2$ , поэтому $\sqrt{5}+2=4+\sqrt{5}-2$ . Снова уничтожим иррациональность в числителе второго слагаемого:

$\sqrt{5}-2 = \frac{1}{\sqrt{5}+2}$

В итоге получилось:

$\sqrt{5} = 2 + \frac{1}{4+\frac{1}{\sqrt{5}+2}}$

Проделаем еще один аналогичный шаг:

$\sqrt{5} = 2 + \frac{1}{4+\frac{1}{4+\frac{1}{\sqrt{5}+2}}}$

Нетрудно заметить, что процесс выделения целой части и образования цепной дроби в данном примере не имеет конца. В каждом новом знаменателе будет появляться и слагаемое $\sqrt{5}-2$ . Поэтому ясно, что $\sqrt{5}$ представляется в виде бесконечной цепной дроби:

$\sqrt{5} = 2, 4, 4, 4, ...$

Гипотеза

Если $d \in \mathbb{N}, \sqrt{d} \notin \mathbb{N}$ , то цепная дробь числа $\sqrt{d} + \sqrt{d}$ чисто периодическая. Эту гипотезу доказал Эварист Галуа.

Т.е. если к непериодической части дроби $1;2,2,2,... = \sqrt{2}$ прибавить целую часть $[\sqrt{2}] =1$ , то получится чисто периодическая дробь

$\sqrt{3} = 1;1,2,... \sqrt{3}+1 = 2,1,...$ $\sqrt{5} = 2;4,4,4,... \sqrt{5}+2 = 4,4,4,...$ $\sqrt{6} = 2;2,4,... \sqrt{6}+2 = 4,2,...$ $\sqrt{13} = 3;1,1,1,1,6,... \sqrt{13}+3 = 6,1,1,1,1,...$

Вычисление в облаке WolframAlpfa

WolframAlpfa производит вычисление цепных дробей с помощью операции continued fraction Вычислим значение $\sqrt{3}$ (проверить по ссылке Вычислим значение $\sqrt{3}+1$ ссылка

Если в разложении корня по методу Бомбелли

$\sqrt{n} =a\pm {\frac {|n-a^{2}|}{2a\pm {\frac {|n-a^{2}|}{2a\pm {\frac {|n-a^{2}|}{2a\pm \cdots }}}}}}$

к первому слагаемому прибавить , получим чисто периодическую дробь

$\sqrt{n}+a =2a\pm {\frac {|n-a^{2}|}{2a\pm {\frac {|n-a^{2}|}{2a\pm {\frac {|n-a^{2}|}{2a\pm \cdots }}}}}}$

Остаётся привести дробь к более привычному виду с единицами в числителе. Разделим числитель и знаменатель дроби на $|n-a^{2}|$ и получим выражение

$\sqrt{n}+a =2 a\pm {\frac {1}{\frac{2a}{|n-a^{2}|} \pm {\frac {1}{2a \pm {\frac {1}{\frac{2a}{|n-a^{2}|}\pm \cdots }}}}}}$

Таким образом display \sqrt{2}+1 = 2+ \frac{1}{\frac{2}{1} + \frac{1}{2 + \frac{1}{\frac{2}{1}+...} } } =2,2,2,... display display \sqrt{3}+1 = 2+ \frac{1}{\frac{2}{2} + \frac{1}{2 + \frac{1}{\frac{2}{2}+...} } } =2,1,... display display \sqrt{5}+2 = 4+ \frac{1}{\frac{4}{1} + \frac{1}{4 + \frac{1}{\frac{4}{1}+...} } } =4,4,4,... display display \sqrt{6}+2 = 4+ \frac{1}{\frac{4}{2} + \frac{1}{4 + \frac{1}{\frac{4}{2}+...} } } =4,2,... display display \sqrt{13}+3 = 6+ \frac{1}{\frac{6}{4} + \frac{1}{6 + \frac{1}{\frac{6}{4}+...} } } =6,\frac{3}{2},... display Напишем программу, вычисляющую приближение цепной дроби inline 6,\frac{3}{2},... inline

#lang racket define continued_fraction ( lambda (n if (= n 0 1 + 6 (/ 1 (+ 3/2 (/ 1 (continued_fraction(- n 1))))) ))) continued_fraction 4 codepad.org На четвёртом шаге получаем inline 6\frac{3818}{6305} inline, что равно inline 6,6055511...inline в то время как inline \sqrt{13}+3 \approx 6.6055512... inline.

Уравнения Пелля

Приближения к квадратному корню можно искать с помощью уравнений Пелля.

"Пусть натуральное число не является квадратом. Легко видеть, что $\sqrt{a}$ не выражается отношением натуральных чисел, т.е. не существует такой обыкновенной дроби $\frac{x}{y}$ , что $(\frac{x}{y})^2=a$

Другими словами, если натуральное число не является точным квадратом, то уравнение

не имеет решения в натуральных числах. Попытаемся в этом случае выразить $\sqrt{a}$ отношением натуральных чисел приближённо.

Если $\sqrt{a}=\frac{x}{y}$ , то $x^2-ay^2 \approx 0$

Самое близкое к нулю натуральное число — это единица. Поэтому дело сводится к решению в натуральных числах диофантова уравнения

которое носит название… уравнения Пелля."

Пояснение

Число, которое не может быть представлено в виде обыкновенной дроби $\frac{x}{y}$ ,где - целые числа, $y \neq 0$ называется иррациональным.

В статье, посвящённой квадратному корню из двух приводится доказательство иррациональности этого числа:

Допустим противное: $\sqrt{2}$ рационален, т.е. представим в виде несократимой дроби $\frac{m}{n}$ , где m-целое число, а n-натуральное число. Возведём предполагаемое равенство в квадрат:

$\sqrt{2}=\frac{m}{n} \rightarrow 2 = \frac{m^2}{n^2} \rightarrow m^2=2n^2$

Отсюда следует, что чётно, значит, чётно и . Пускай , где целое. Тогда $4k^2=n^2 \rightarrow 2k=n$

Следовательно, чётно, значит, чётно и . Мы получили, что и чётны, что противоречит несократимости дроби $\frac{m}{n}$

Значит, исходное предположение было неверным, $\sqrt{2}$ — иррациональное число.

Это означает (по Аристотелю), что

Диагональ квадрата несоизмерима с его стороной, так как если предполагать их соизмеримость, то нечётные числа равны чётным.

Доказательство иррациональности корня из простого числа следующее

Предположим, что существует несократимая дробь $\frac{m}{n}$ , такая что $\sqrt{p}=\frac{m}{n}$

Тогда, $p=\frac{m^2}{n^2} \rightarrow pn^2=m^2$

Если входит в произведение сомножителей факторизации числа , то то это число входит в произведение сомножителей факторизации числа , т.е. число делится на.

Представим как , тогда $p^2k^2=pn^2 \rightarrow pk^2=n^2$

Значит и делится на

Отсюда следует, что несократимую дробь $\frac{m}{n}$ можно сократить на (пришли к противоречию)

***

Золотая парабола

Возвращаясь к уравнению $x = 1 + \frac{1}{x} \leftrightarrow\ x^2-x-1=0$

Как было сказано выше, решением данного уравнения является золотое сечение, т.е. соотношение сторон открытки, остающейся себе подобной при отрезании квадрата, стороной которого является меньшая сторона открытки.

В прямоугольнике стороны

Если принять сторону AB за , то сторона BE прямоугольника BEFC будет равна и вследствие подобия прямоугольников BEFC и ABCD справедливо соотношение

$\frac{x}{1}=\frac{1}{x-1} \leftrightarrow\ x(x-1)=1 \leftrightarrow\ x^2-x-1=0$

Таким же образом ведётся построение золотого треугольника (это равнобедренный треугольник, в котором боковые стороны находятся в золотой пропорции с основанием).

В золотом треугольнике углы при основании равны $72^{\circ}$ ;

угол, лежащий против основания равен $36^{\circ}$

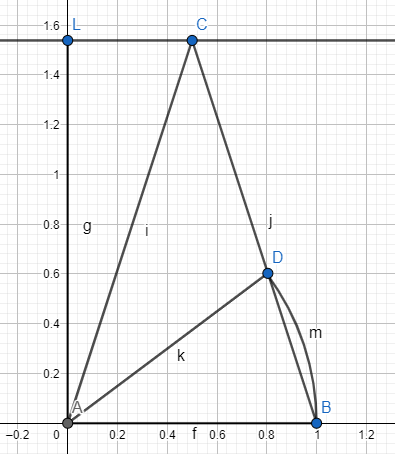
Проведём биссектрису угла при основании. Эта биссектриса является боковой стороной равнобедренного треугольника АВD, следовательно равняется единице. Также она является боковой стороной равнобедренного треугольника ACD, следовательно отрезок CD равняется единице. По теореме о биссектрисе, которая гласит, что "биссектриса при вершине треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам" получим пропорцию $\frac{AC}{AB}=\frac{CD}{BD}$

Приняв AC=BC за и BD за получим идентичную предыдущей пропорцию $\frac{x}{1}=\frac{1}{x-1} \leftrightarrow\ x(x-1)=1 \leftrightarrow\ x^2-x-1=0$

Воспользуемся теоремой Виета для решения этого уравнения

$(x-x_{1})(x-x_{2})=0$ $x^2-xx_{2}-xx_{1}+x_{1}x_{2}=0$ $x^2-(x_{1}+x_{2})x+x_{1}x_{2}=0$ $x_{1}+x_{2}=-p$ $x_{1}x_{2}=q$

Коэффициенты параболы

Значит, сумма корней $\sum x_{1}x_{2}=1$

Произведение корней $\prod x_{1}x_{2}=-1$

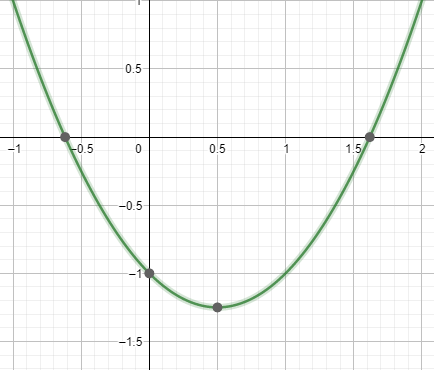
Будем приближаться к золотому сечению, увеличивая расстояние между точками пересечений ветвей параболы с осью абсцисс до тех пор, пока произведение корней уравнения не превысит единицу ( т.е. не станет меньшим -1), уменьшая разряд числа на порядок. Примем inline x_{1}=1.5inline и inline x_{2}=-0.5 inline и будем увеличивать расстояние между точками пересечений ветвей параболы с осью абсцисс на 0.1 При inline x_{1}=1.5inline и inline x_{2}=-0.5 inline произведение inline x_{1}x_{2}=-0.75 inline При inline x_{1}=1.7inline и inline x_{2}=-0.7 inline произведение inline x_{1}x_{2}=-1.19 inline Уменьшаем шаг до 0.01 При inline x_{1}=1.62inline и inline x_{2}=-0.62 inline произведение inline x_{1}x_{2}=-1.0044 inline Уменьшаем шаг до 0.001 При inline x_{1}=1.611inline и inline x_{2}=-0.611 inline произведение inline x_{1}x_{2}=-0.984321 inline При inline x_{1}=1.612inline и inline x_{2}=-0.612 inline произведение inline x_{1}x_{2}=-0.986544 inline При inline x_{1}=1.613inline и inline x_{2}=-0.613 inline произведение inline x_{1}x_{2}=-0.988769 inline и т.д. Напишем программу, реализующую данный метод def fooa,b,s,n: step=s counter=n x1=a+step x2=b+step if x1*x2<1: foox1,x2,step,counter else: #if x1*x2>1 if counter>0: printcounter x1=x1-step x2=x2-step phi=x1 printphi step=step/10 counter=counter-1 foox1,x2,step,counter foo1.5,0.5,0.1,10 На десятом шаге получаем приближение, равное 1.6180339887

P.S. Задача 27. Доказать, что остаток от деления числа inline 2^{p-1} inline на простое нечетное число inline p inline равен inline 1 inline примеры: $inline$ 2^{2} = 3a+1, 2^{4}=5b+1, 2^{6}=7c+1, 2^{10} -1 = 1023 = 10 \cdot 93 inline. из задачника В.И. Арнольда рассматривается в статье Удивительные приключения цепных дробей журнала "Квант".

Статья, в которой содержится информация о цепных дробях "Об одной задаче, которую больше не предлагают на собеседовании" ссылка

Книги

Задачи для детей от 5 до 15 лет В. И. Арнольд

Курс дифференциального и интегрального исчисления Г. М. Фихтенгольц

Теория чисел А. А. Бухштаб

За страницами учебника математики Н. Я. Виленкин, Л. П. Шибасов, З. Ф. Шибасова Алгебра Н. Я. Виленкин, Р. С. Гутер, С. И. Шварцбурд

Метод математической индукции И.С. Соминский

Digital Arithmetic Ercegovac Milos D., Lang Tomas/

Math first

Рассмотрим ещё один пример из задачника

Извлечение квадратного корня

Уравнения Пелля

Золотая парабола

Комментарии (0)