Алгоритм ECDSA (Elliptic Curve Digital Signature Algorithm) — это реализация схемы цифровой подписи, основанная на использовании эллиптических кривых и модульной арифметики.

Мы оставим подробный разбор всех тонкостей этого алгоритма и соответствующей математической теории для будущих статей. Здесь же просто покажем основные идеи, за счет которых в ECDSA реализуются алгоритмы KeyGen, Sig и Ver.

Модульную арифметику пока полностью оставим в стороне. Эта тема несложная, но требует подробного рассмотрения. Поговорим сейчас только об эллиптических кривых — для начала нам этого будет достаточно.

Эллиптическая кривая в ECDSA — это линия на плоскости, задаваемая уравнением y²=x³+a∙x+b, где a и b — такие числа, что 4∙a³+27∙b²≠0. Например, Bitcoin и Ethereum используют кривую y²=x³+7 (рис. 1).

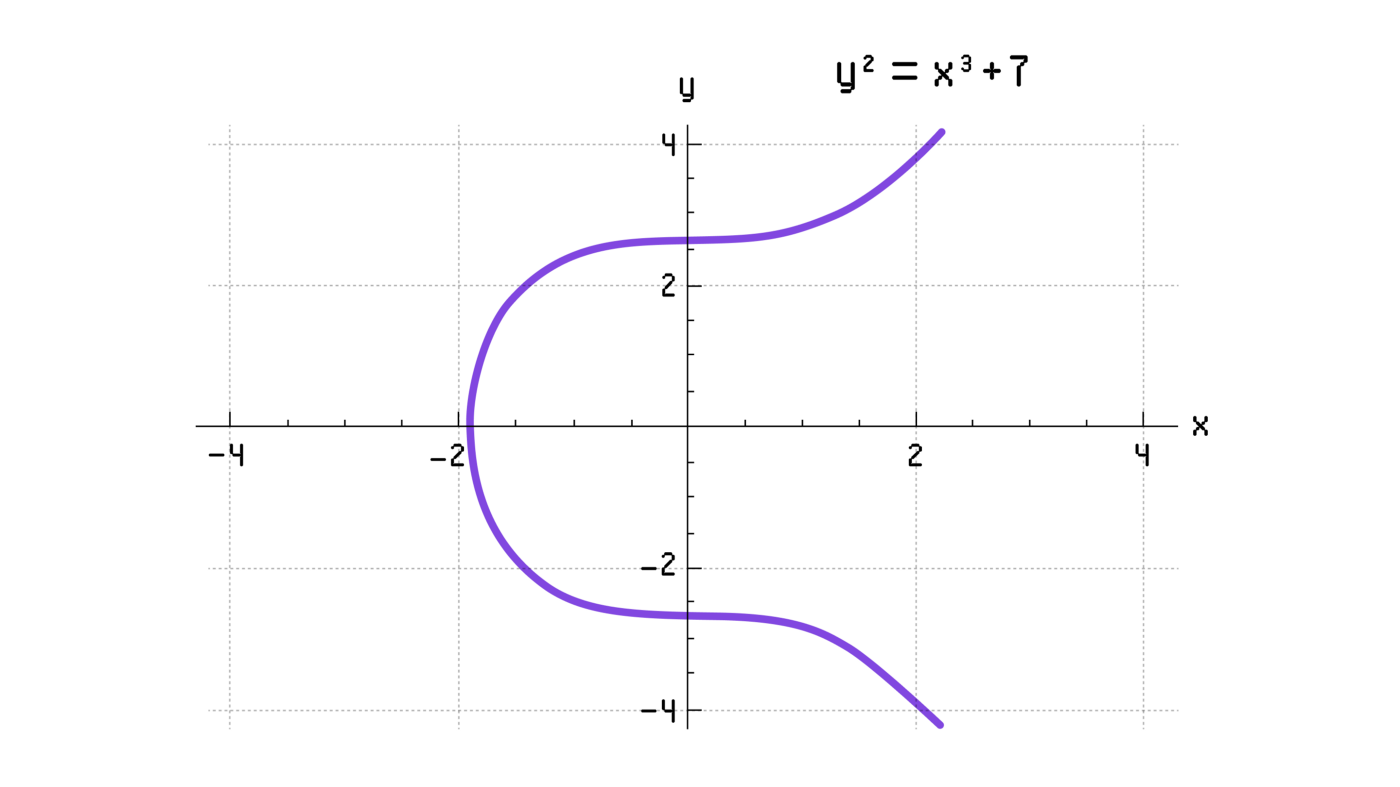
Главная особенность эллиптической кривой заключается в том, что ее точки можно по особому правилу умножать на целые положительные числа. При таком умножении¹. В результате точка перемещается определенным образом.

Если G — точка на кривой, а k — число, то для новой точки k∙G есть три варианта расположения:

1. k∙G=G, то есть умножение на k ничего не делает и точка k∙G совпадает с G. Например, умножение на единицу всегда оставляет точку на месте: 1∙G=G для любой G. Тут работает аналогия с обычными числами — умножение на 1 не меняет исходного числа. Так же и с точкой — ее положение на кривой не меняется.

2. k∙G не совпадает с G, но при этом все равно лежит на кривой. То есть в результате умножения на q точка как-то скользит вдоль кривой. На Рис. 2 приведена схема перемещений конкретной точки P по кривой y²=x³+7 при умножении на числа от 1 до 7.

3. Точки k∙G не существует. На практике это означает, что в формулах для подсчета ее координат встретилось деление на 0. В этом случае используется специальная терминология: говорят, что k∙G — это бесконечно удаленная точка и пишут k∙G=〇. 
   Например, если точка G лежит на пересечении кривой с осью x, то всегда 2∙G=〇.

Операция умножения точки на число обладает одним интересным свойством. Пусть для точки G на кривой существует такое n, для которого n∙G=〇 и пусть n наименьшее из положительных целых чисел, удовлетворяющих этому условию. Тогда среди точек G, 2∙G, …, (n-1)∙G нет совпадающих — они все разные. Более того, при умножении точки G на числа, большие n, ее перемещения по кривой зацикливаются: (n+1)∙G=G, (n+2)∙G=2∙G, …, (n+k)∙G=k∙G для любого k>0.

Таким образом, у точки G есть всего n-1 возможных позиций на кривой, куда она может переместиться в результате умножения на число. С учетом бесконечно удаленной точки 〇 получаем суммарно n возможных результатов для произведения k∙G: G, 2∙G, …, (n-1)∙G, или 〇. Число n в этой ситуации называется порядком точки G. У произвольной точки на кривой может существовать порядок, а может и не существовать. 

Например, как мы видели ранее, если точка G лежит на оси x, то 2∙G=〇. Число 2 является наименьшим целым положительным числом с таким свойством, поскольку 1∙G=G≠〇. Следовательно, для точек пересечения кривой с осью x существует всего два возможных исхода умножения на число k. Если k нечетное, то точка остается на месте, а если k четное, то точка уходит на бесконечность. Таким образом, у таких точек есть порядок и он равен 2.

Теперь рассмотрим точку G, для которой не существует такого числа n, что n∙G=〇. В таком случае оказывается, что если начать умножать точку G на всевозможные положительные целые числа, то каждый раз будет получаться новый результат. То есть, в отличие от предыдущего случая, у точки G будет бесконечно много возможных позиций на кривой и она будет менять их без повторений. В этой ситуации говорят, что порядок такой точки G равен бесконечности или что точка G имеет бесконечный порядок.

Таким образом, слово порядок используется для того, чтобы показать, сколько разных результатов можно получить, умножая току на всевозможные целые положительные числа.

Порядок точки G является конечным числом тогда и только тогда, когда существует такое n, что n∙G=〇. И порядок точки G является бесконечным тогда и только тогда, когда такого n нет. 

Переходим к алгоритму ECDSA. Алгоритм ECDSA предполагает, что в системе заранее выбрано пять параметров, одинаковых для всех пользователей. Два из них относятся к модульной арифметики в ECDSA, поэтому о них мы пока говорить не будем. Обсудим остальные три.

Первый параметр — это сама эллиптическая кривая. Чтобы определить кривую, достаточно просто выбрать два числа a и b из ее уравнения y²=x³+a∙x+b, 4∙a³+27∙b²≠0.

Второй параметр — это какое-то простое число n. Напомним, что простым называется целое положительное число, которое делится только на единицу и на себя.

Третий параметр — это такая точка G на кривой (выбранной на первом шаге), что n является порядком G. Точка G называется базовой точкой. 

Например, Ethereum и Bitcoin используют следующие значения:
a=0, b=7,
n=FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141,
G=x, y, где
x=79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798,
y=483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8.

Мы подробно рассмотрим выбор этих трех параметров в следующих публикациях, а сейчас перейдем к алгоритмам KeyGen, Sig and Ver в ECDSA.

Алгоритм создания ключей KeyGen

Секретный ключ sk выбирается случайным образом от 1 до n-1. В качестве публичного ключа pk берется точка pk=sk∙G. 

Здесь в силу вступает еще одно ключевое свойство операции умножения точки на число. Пусть даны точки G и  d∙G, где d неизвестно. Тогда оказывается, что найти d — это неразрешимая с вычислительной точки зрения задача. Этот факт называется проблемой дискретного логарифмирования для эллиптических кривых.

Отсюда следует, что, зная базовую точку G и публичный ключ pk, мы никак не сможем найти соответствующий секретный ключ sk. 

При этом, поскольку порядок точки G равен n, у нее есть всего n-1 возможная позиция на кривой, а значит, для публичного ключа существует всего n-1 возможное значение.

На выходе алгоритм выдает пару sk, pk, где sk — число, а pk — точка, то есть пара чисел.

Алгоритм создания подписи Sig

Алгоритм генерации подписи Sig принимает на вход приватный ключ sk и число m — хеш подписываемого сообщения.

А на выходе в качестве подписи выдается не одно число, а два: (r, s)=Sig(sk, m). Почему два, а не одно?

Это связано с тем, что внутри самого алгоритма присутствует выбор дополнительного случайного числа k, влияющего на вид подписи. Этот случайный параметр нужен для того, чтобы обеспечить секретность ключу sk. Если подпись полностью определятся лишь входными параметрами sk и m, то секретный ключ sk может быть вычислен на основе всего лишь двух оставленных с его помощью подписей.

Наличие случайного параметра приводит к тому, что на одних и тех же входных значениях алгоритм Sig может выдавать разный результат. Поэтому, чтобы подпись можно было проверить, необходимо поделиться некоторой информацией о параметре k. Первая компонента подписи r как раз содержит в себе эту информацию. Число r полностью определяется числом k, при его подсчете sk и m не используются. В то же время в вычислениях числа s участвуют уже все три параметра k, sk и m.

Алгоритм проверки подписи Ver

Алгоритм проверки подписи Ver принимает на вход публичный ключ pk, хеш сообщения m и подпись (r, s).

На основе подписи и хеша этот алгоритм находит два числа u₁ и u₂. Далее рассматриваются две точки на эллиптической кривой: u₁∙G и u₂∙pk (pk — точка, значит, u₂∙pk — тоже точка). 

Если подпись s была действительно посчитана с помощью ключа sk, соответствующего ключу pk, и сообщение действительно не менялось с момента создания подписи, то точки u₁∙G и u₂∙pk будут находится относительно друг друга в некотором специальном положении. Алгоритм Ver смотрит, так это или нет. Если расположение точек относительно друг друга и правда такое, какое должно быть, то подпись считается корректной, и Ver возвращает 1 (TRUE). В противном случае возвращается 0 (FALSE).

Специальная формула¹ — дополнительно расскажем в наших публикациях

Авторы:

Алексей Трошичев Вдохновитель
Артём Фомичев Математик
Инга Пашенцева Редактор
Александр Половьян Проверка фактов

Использованная литература

1. Don Johnson, Alfred Menezes, “The Elliptic Curve Digital Signature Algorithm (ECDSA)” 

2. William Stein, “Elementary Number Theory: Primes, Congruences, and Secrets”

В следующей статье мы перейдём к описанию пороговой подписи.