В этой статье мы рассмотрим несколько полезных и эффективных алгоритмов для эллиптической кривой E над полем GF(p) , заданной коротким уравнением Вейерштрасса

у^2 = х^3 + Ах + В 

•  Алгоритм генерации точки на кривой E

•  Алгоритм добавления точек

•  Алгоритм удвоения точек

•  Алгоритм нахождения целой кратной точки

•  Алгоритм нахождения целой кратной точки (скалярное умножение)

•  Алгоритм построения делителя D над кривой E с носителем supp(D) заданного размера d

•  Алгоритм Миллера для вычисления значения функции Вейля f _{n, P} по делителю D такому, что supp(D) ∩ {P, O} = ∅

•  Pairing Weil (Спаривание Вейля)

Модульные операции (целые числа) в конечном поле (или поле Галуа)

1. x mod n означает «остаток n от деления x». Другими словами, если x = an + b и a, b ∈ integer, а также 0 ≤ b ≤ n − 1, то x mod n = b .

2. Обратное : если ax = 1 mod n , то a является обратным значением x mod n . Есть два популярных метода решения :• Метод 1 : Попробуйте каждое значение для a < n, пока xa mod n = 1 .• Метод 2 : евклидов метод, который обычно используется для решения обратной задачи больших целых чисел, поэтому рекомендуется использовать метод 1 для решения обратной задачи малых целых чисел.

Операция с точками эллиптической кривой

Точка P(x ₀ , y ₀ ) на эллиптической кривой E означает: ее координаты x ₀ и y ₀ являются элементами поля, а координаты x ₀ и y ₀ удовлетворяют уравнению.

1. Добавление точек на эллиптической кривой : пусть P, Q и R будут тремя точками на эллиптической кривой. Добавление очков P + Q = R.

2. Удвоение точек на эллиптической кривой : пусть P, Q — две точки на эллиптической кривой. Удвоение очков P + P = 2P = Q

3. Скалярное умножение : пусть P будет точкой на кривой E , определенной в уравнении
   

   • Скалярное умножение nP определяется как nP = P + P + P + … + P ( n раз), где n — целое число; nP также является точкой на той же кривой E .

   • Минимальное натуральное число a при aP = O называется порядком P .

   • Скалярное умножение широко требуется в криптосистемах с эллиптическими кривыми.

Делитель

Divisor (Делитель) D на кривой E — это удобный способ обозначить мультимножество точек на E , записанное в виде формальной суммы

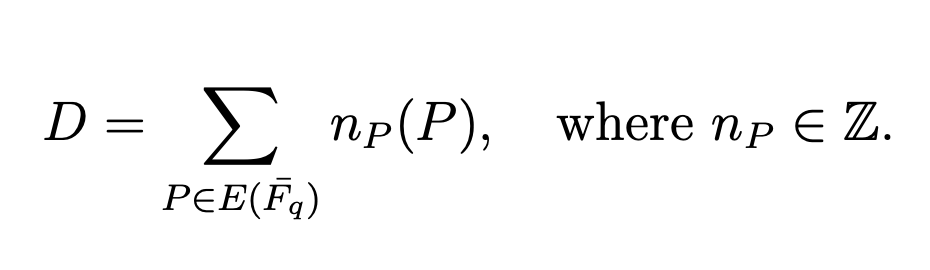
• Множество всех делителей на E обозначается Div _F q (E) и образует группу, в которой сложение делителей естественно.

• Делитель нуля: это делитель для всех n _P = 0, делитель нуля 0 ∈ Div _F q (E) .

• Если поле F _q не является конкретным, его можно опустить и просто записать как Div(E) для обозначения группы делителей.

Делитель функции f на E

Делитель функции f на E используется для обозначения точек пересечения (и их кратностей) функций f и E .

Pairing Weil

Спаривание Вейля, которое обозначается e m , принимает на вход пару точек P, Q ∈ E[m] и дает на выходе корень _m из единицы e m( P , Q) . Билинейность спаривания Вейля выражается уравнениями

e _m (P ₁ + P ₂ , Q) = e _m (P ₁ , Q) * e _m (P2, В),

e _m (P, Q ₁ + Q ₂ ) = e _m (P, Q ₁ ) * e _m (P, Q ₂ ).

Пара Вейля P и Q — это количество

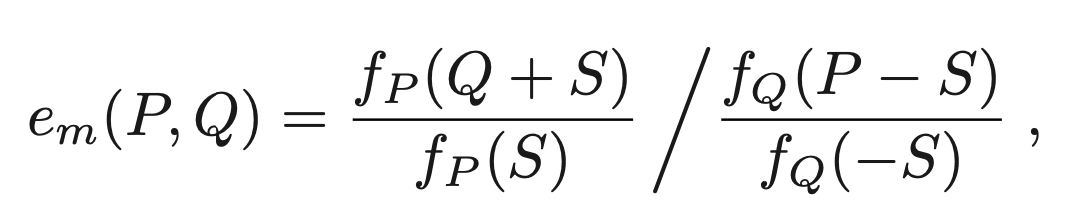
где S ∈ E — любая точка, удовлетворяющая условию S ∉ {O, P, −Q, P − Q} . (Это гарантирует, что все величины в правой части определены и отличны от нуля.) Можно проверить, что значение e _m (P,Q) не зависит от выбора f _P , f _Q и S .

Эффективный алгоритм вычисления спаривания Вейля

Пусть E — эллиптическая кривая, и пусть P = (x _P ,y _P ) и Q = (x _Q , y _Q ) — ненулевые точки на E .

Пусть λ будет наклоном линии, соединяющей P и Q , или наклоном касательной к E в P, если P = Q. (Если линия вертикальна, мы полагаем λ = ∞.) Определим функцию g _{P, Q} на E следующим образом:

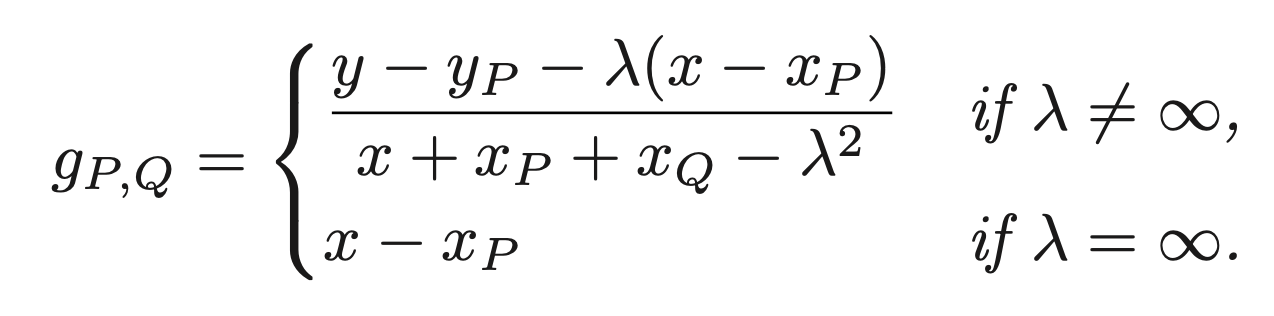
затем

div(g _{P, Q} ) = [P] + [Q] — [P + Q] — [ O ].

Алгоритм Миллера

Пусть m ≥ и запишите двоичное расширение m как

m = m ₀ + m ₁ * 2 + m ₂ * 2 ² +···+ m _{n — 1} 2 ^{n — 1}

при m _i ∈ {0, 1} и m _{n — 1} ≠ 0 . Следующий алгоритм возвращает функцию f _P , делитель которой удовлетворяет условию

div( f _P ) = m [ P ] — [ mP ] — ( m — 1 ) [ O ],

где функции g _{T, T} и g _{T, P,} используемые алгоритмом, определены в (a).

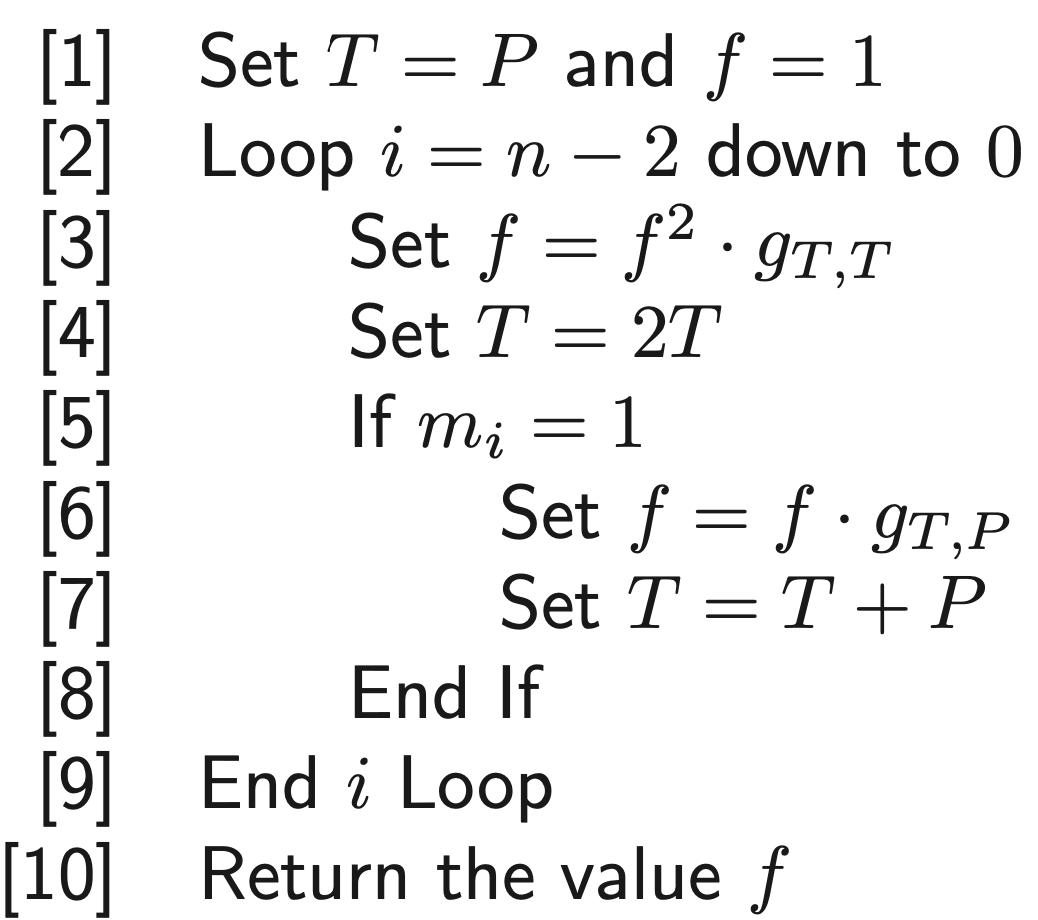
В частности, если P ∈ E[m] , то div( f _P ) = m [ P ] − m [ O ].

Требование

• Python 3.5

• numpy

git clone https://github.com/demining/CryptoDeepTools.git

cd CryptoDeepTools/04AlgorithmsForSecp256k/

pip3 install numpy

├── Curves.py             <- Набор данных эллиптических кривых
├── Divisor.py            <- Создать делитель
├── EllipticCurve.py      <- Классы эллиптической кривой и точки на эллиптической кривой
├── EuclideanAlg.py       <- Расширенный алгоритм Евклида
├── Helper.py             <- Вспомогательные функции (обратные биты, мощность по модулю) 
├── Pairing.py            <- Спаривания Вейля, а так же Алгоритм Миллера
├── Tests.py              <- Модульные тесты для функций
├── Tonelli_ShanksAlg.py  <- Алгоритм Тонелли – Шенкса
├── main.py               <- main

Исходный код

Telegram: https://t.me/cryptodeeptech

Видеоматериал: https://youtu.be/gFbiBCNPsFk

Источник: https://cryptodeep.ru/algorithms-for-secp256k/