Эта задача была предложена мне на одном из курсов по Java. В статье излагаю своё решение, а также анализ его эффективности. Обработка IP адресов необходима для многих проектов, и я надеюсь, что алгоритмы, описанные в этой статье, могут быть полезны.

Задача

В текстовом файле содержится список IPv4 адресов в десятичной записи. В каждой строчке ровно один адрес, как на примере ниже:

145.67.23.4
8.34.5.23
89.54.3.124
89.54.3.124
3.45.71.5
...

Задача написать программу для подсчёта количества уникальных адресов в данном файле. Адреса корректны, их не нужно дополнительно проверять. Однако количество адресов может быть достаточно большим, вплоть до нескольких миллиардов. Нам нужно написать программу, расходующую минимум памяти и ресурсов процессора.

В качестве примера предлагается текстовый файл: https://ecwid-vgv-storage.s3.eu-central-1.amazonaws.com/ip_addresses.zip. В распакованном виде этот файл занимает почти 120 Gb, в нём 8 миллиардов адресов, из которых один миллиард уникальных.

Командная строка

В случае небольших текстовых файлов писать отдельную программу не обязательно, — для выполнения этой задачи мы можем использовать команды операционной системы. Например, в системе Linux команда будет выглядеть так:

sort -u ips.txt | wc -l

Но на больших файлах время выполнения будет очень значительным. В итоге, вместо результата мы получим сообщение об ошибке:

sort: write failed: /tmp/sortcQjXmj: No space left on device 
0

Пишем программу

Итак, приступаем к написанию программы для решения этой задачи. Будем использовать возможности современной версии Java, такие как Stream API.

Для чтения файла используем статический метод lines(Path path) класса Files, который возвращает поток строк. Каждая строка - это текстовое представление адреса в десятичной записи. Наша задача - подсчитать количество уникальных адресов.

Схема программы будет выглядеть примерно так:

class IPCounter {
    public static void main(String[] args) {
        var path = Path.of("ips.txt");
        try (var lines = Files.lines(path)) {

            // подсчёт количества уникальных адресов
            var unique = ... 

            System.out.println(unique);
        } catch (IOException e) {
            System.err.println(e.getMessage());
        }
    }
}

Здесь мы предполагаем, что текстовый файл называется "ips.txt" и находится в рабочем каталоге программы. Для краткости напрямую используем имя файла в коде программы. Также, опускаем строки импорта.

Нам остаётся добавить код для подсчёта уникальных адресов, и ниже мы разберём возможные варианты.

Наивный способ

Наша первая попытка решить эту задачу будет выглядеть так:

var unique = lines.distinct().count();    

Так же, как и в случае с командной строкой, это решение будет работать лишь на небольших объёмах данных. На нашем тестовом файле в 120 Gb программа, запущенная на персональном компьютере с 8 Gb RAM, завершилась с ошибкой:

Exception in thread "main" java.lang.OutOfMemoryError: Java heap space
...

Действительно, для работы программе нужно сохранить миллиард уникальных объектов-строк. На 64-разрядной JVM минимальный размер объекта равен 16 байтам, и для хранения миллиарда объектов потребуется минимум 16 Gb памяти. Если же мы говорим о конкретных строках, представляющих адреса, то их длина варьируется от 7 до 15 символов, и такие объекты будут занимать в памяти размер 24 или 32 байта. Понятно, что если это решение и будет работать, то только на очень мощном компьютере с большим объёмом памяти.

Преобразуем строки в числа

Первое, что можно сделать для уменьшения объёма данных,— преобразовать представление адреса из текстового в бинарный формат. Интернет протокол четвёртой версии (IPv4) использует 32-битные (4-х байтные) адреса.

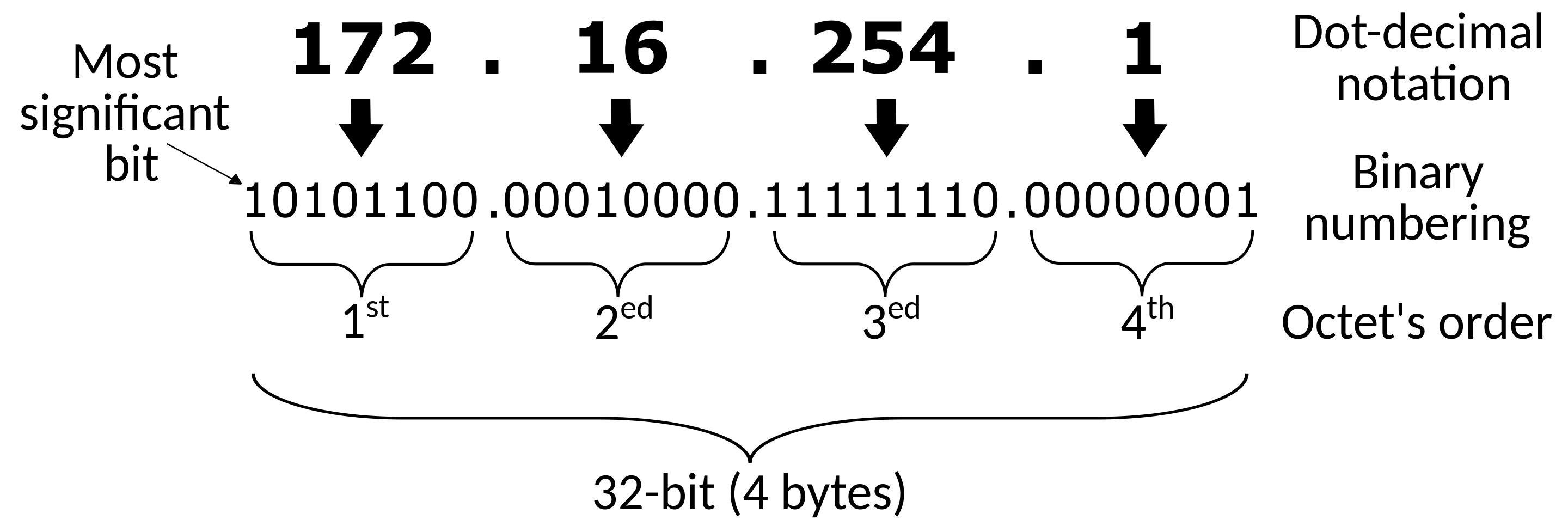
В нашем текстовом файле адреса записаны в виде четырёх десятичных чисел от 0 до 255, разделённых точками. Мы преобразуем каждое из таких чисел в байт и объединим их в целое число типа int. Таким образом каждый адрес будет занимать ровно 4 байта.

Попробуем погуглить и использовать готовый алгоритм. Например, один из алгоритмов на сайте Mkyong. Для удобства создадим отдельный класс, это позволит нам в дальнейшем легко заменить конвертер на оптимальный.

public class MkyongConverter implements ToIntFunction<String> {

    @Override
    public int applyAsInt(String ipAddress) {
        var ipAddressInArray = ipAddress.split("\\.");
        long result = 0;
        for (int i = 0; i < ipAddressInArray.length; i++) {
            int power = 3 - i;
            int ip = Integer.parseInt(ipAddressInArray[i]);
            result += ip * Math.pow(256, power);
        }
        return (int) result;
    }
}

Теперь перепишем нашу программу с использованием конвертера:

var converter = new MkyongConverter();

var unique = lines
				.mapToInt(converter)
				.distinct()
				.count();

К сожалению, при запуске программы мы получаем то же сообщение об ошибке, что и в предыдущий раз: OutOfMemoryError. Это происходит из-за того, что метод distinct() не имеет специализированной реализации для целых чисел. Если вы посмотрите исходный код реализации, то увидите, что происходит “упаковка” чисел с преобразованием в обычный стрим объектов, а затем вызов метода distinct() для обычного стрима. Если целое число занимает в памяти 4 байта, то обёртка в четыре раза больше - 16 байт.

Для решения этой проблемы мы должны создать и использовать наш собственный, оптимизированный, контейнер для представления множества целых чисел.

Контейнер для чисел

Для начала определим, какой интерфейс должен быть у нашего контейнера. Добавим самый минимум методов, необходимый для решения нашей задачи.

Мы будем использовать метод collect целочисленного стрима, поэтому посмотрим на сигнатуру этого метода:

<R> R collect(Supplier<R> supplier,
              ObjIntConsumer<R> accumulator,
              BiConsumer<R,R> combiner)

Здесь R — тип изменяемого контейнера результатов. Параметр supplier создаёт (поставляет) наш контейнер, accumulator принимает на вход контейнер и целое число, а combiner принимает на вход два контейнера и объединяет их. Последний используется, когда необходимо объединить паралельные стримы.

Так как мы будем использовать только последовательный стрим, то можно опустить реализацию метода addAll. Также контейнеру понадобится метод, который вернёт количество собранных уникальных адресов. На основании всего вышеперечисленного определяем интерфейс для нашего контейнера:

public interface IntContainer {
    // accumulator
    void add(int number); 

    // combiner
    default void addAll(IntContainer other) {
        throw new UnsupportedOperationException();
    }

    long countUnique();
}

Следующий вопрос, который нужно решить — как именно сохранять информацию.

Если у нас порядка миллиарда чисел, каждое из которых занимает 4 байта, то для их хранения нам нужно 4Gb информации. Но можно хранить не сами числа, а только информацию о том, есть ли такое число или нет. А для этого нам потребуется всего один бит. Для целых чисел типа int нужно 2³² бит, что равно 512Mb. Это значение фиксированное и не зависит от общего количества чисел, которые нужно обработать.

В Java для работы с множеством битов есть класс BitSet, который вполне подходит для наших целей.

Учтём, что индекс бита может быть от 0 до Integer.MAX_VALUE, а нам требуется сохранять информацию не только о положительных числах, но и об отрицательных. Поэтому мы создаём два сета, один для положительных чисел, второй — для отрицательных. Вот простая реализация интерфейса для контейнера, в которой мы определяем два битовых сета:

public class DualBitSetContainer implements IntContainer {
    private final BitSet positive = new BitSet(Integer.MAX_VALUE);
    private final BitSet negative = new BitSet(Integer.MAX_VALUE);

    @Override
    public void add(int i) {
        if (i >= 0) {
            positive.set(i);
        } else {
            negative.set(~i);
        }
    }

    @Override
    public long countUnique() {
        return (long) positive.cardinality() + negative.cardinality();
    }
}

Теперь подсчёт уникальных адресов будет выглядеть следующим образом:

var unique = lines
        .mapToInt(converter)
        .collect(DualBitSetContainer::new, IntContainer::add, IntContainer::addAll)
        .countUnique();

Когда мы запустим наше приложение, программа, хоть и не быстро, но успешно прочитает и обработает тестовый файл и выдаст правильный результат: 1,000,000,000 уникальных адресов.

Оптимизируем конвертер

Вернёмся к алгоритму конвертации адреса из текстового представления в число. Мы взяли готовый алгоритм из интернета. Но насколько он хорош? К сожалению, как и многие готовые решения из интернета, этот код далёк от оптимального.

Рассмотрим эту строчку:

var ipAddressInArray = ipAddress.split("\\.");

Основная проблема с производительностью в том, что здесь создаются пять новых объектов — четыре строки и массив. Эти новые объекты используются только в пределах метода и после его завершения должны быть собраны уборщиком мусора. Создание объекта — затратная операция. Виртуальная машина должна выделить и инициализировать память для этих объектов, а после работы метода эти объекты остаются в памяти до тех пор, пока не будут обработаны сборщиком мусора.

Вторая строка, на которую нужно обратить внимание, это преобразование строк в числа:

int ip = Integer.parseInt(ipAddressInArray[i]);

Здесь метод Integer::parseInt проводит проверку входных данных и может выкинуть исключение NumberFormatException.

К сожалению, это не может считаться проверкой адреса на правильность, так как метод пропускает все числа за пределами допустимого диапазона от 0 до 255. Если у нас стоит задача проверять IP адреса, то можно использовать класс InetAddress. Например, мы можем сконвертировать адрес с помощью такого кода:

String ipAddress = "172.16.254.1";

int ip = ByteBuffer.allocate(Integer.BYTES)
            .put(InetAddress.getByName(ipAddress).getAddress())
            .getInt(0);

В случае некорректного адреса метод InetAddress::getByName выкидывает проверяемое исключение UnknownHostException, которое мы должны перехватить и обработать.

Однако, по условию задачи, все адреса корректные. Нам не нужно проводить дополнительную проверку их правильности.

Что нужно, чтобы написать оптимальный метод? Во-первых, мы должны избегать создания ненужных временных объектов. Во-вторых, нам не нужно использовать сложные встроенные методы для парсинга чисел, если мы можем написать собственный простой алгоритм. Попробуем написать конвертер, удовлетворяющий этим условиям:

public class OptimizedConverter implements ToIntFunction<CharSequence> {
    private static final int DECIMAL_BASE = 10;

    @Override
    public int applyAsInt(CharSequence ipAddress) {
        int base = 0;
        int part = 0;

        for (int i = 0, n = ipAddress.length(); i < n; ++i) {
            char symbol = ipAddress.charAt(i);
            if (symbol == '.') {
                base = (base << Byte.SIZE) | part;
                part = 0;
            } else {
                part = part * DECIMAL_BASE + symbol - '0';
            }
        }
        return  (base << Byte.SIZE) | part;
    }
}

В этом алгоритме мы избегаем создания объектов и не используем “тяжёлые” методы для конвертации текста в число. Обратите внимание, мы не вызываем специальные методы класса String и поэтому можем использовать более общий интерфейс CharSequence. Это позволяет передавать в качестве параметра метода не только объекты класса String но и объекты других классов, поддерживающих этот интерфейс, например, StringBuilder.

Сравнение конвертеров

Давайте посмотрим, насколько у нас получилось улучшить быстродействие алгоритма. Для этого мы используем фреймворк JMH. Мы проводим замер скорости работы конверторов для трёх адресов разной длины. Ниже приведены результаты замера:

Как видим, для всех типов адресов наша собственная реализация работает на порядок быстрее, чем готовое решение, скопированное из интернета.

Оптимизируем контейнер

Релизация контейнера, использующая два битсета, является простой и достаточно эффективной. Однако мы можем немного улучшить эту реализацию. Универсальный класс BitSet содержит различные проверки, которые мы можем исключить в нашей собственной реализации.

В качестве основы реализации мы используем массив целых чисел типа long. Так как этот тип занимает в памяти 8 байт или 64 бита, мы можем использовать одно такое число в качестве сета для 64 чисел. Входной параметр, представляющий IPv4 адрес, занимает в памяти 32 бита. Мы разбиваем его на две части. Первая часть, 6 битов, будет значением (число от 0 до 63). Вторая часть размером 24 бита будет представлять индекс массива, где хранится это значение.

Ниже представлен пример реализации контейнера, основанный на массиве:

public class LongArrayContainer implements IntContainer {
    private static final int VALUE_SIZE = 6;
    private static final int VALUE_MASK = 077;
    private static final int STORAGE_SIZE = 1 << (Integer.SIZE - VALUE_SIZE + 1);

    private final long[] storage = new long[STORAGE_SIZE];

    @Override
    public void add(final int number) {
        final int index = number >>> VALUE_SIZE;
        final int value = number & VALUE_MASK;
        
        storage[index] |= 1L << value;
    }

    @Override
    public long countUnique() {
        return Arrays.stream(storage).map(Long::bitCount).sum();
    }
}

Данная реализация хорошо подходит для случая, когда у нас большое количество IPv4 адресов, случайно распределённых на всём возможном диапазоне. Недостаток этой реализации в том, что мы сразу выделяем 512Мб памяти.

На практике нам может потребоваться обрабатывать адреса только каких-то конкретных сегментов, например, отдельной страны. При этом многих сегментов может не быть совсем. В этом случае мы можем оптимизировать нашу реализацию по памяти, немного проиграв в производительности.

Для этой реализации мы создадим массив BitSet, где каждый индекс массива представляет собой определённый сегмент сети, при этом мы не выделяем память при инициализации BitSet. Память будет выделяться динамически, по мере необходимости. При создании контейнера мы можем задать размер сегмента.

Ниже приведён пример реализации. Здесь параметер level в конструкторе определяет количество битов для индекса массива, и может быть от 1 до 16. При уровне 1 мы получаем аналог DualBitSetContainer с динамическим выделением памяти. Наиболее оптимальным представляется уровень 8, когда создаётся массив размером 256 ячеек. В этом случае, для адресов вида 192.xxx.xxx.xxx будет выделено только 2Мб памяти под каждый сегмент.

public class BitSetContainer implements IntContainer {
    private final BitSet[] storage;
    private final int mask;
    private final int shift;

    public BitSetContainer(int level) {
        Objects.checkIndex(level - 1, Byte.SIZE * 2);
        mask = 0xFFFF_FFFF >>> level;
        shift = Integer.SIZE - level;
        storage = Stream.generate(BitSet::new).limit(1L << level).toArray(BitSet[]::new);
    }

    @Override
    public void add(int ip) {
        storage[ip >>> shift].set(ip & mask);
    }

    @Override
    public long countUnique() {
        return Arrays.stream(storage).mapToLong(BitSet::cardinality).sum();
    }
}

Перепишем нашу программу с использованием последнего контейнера:

ToIntFunction<CharSequence> converter = new OptimizedConverter();
Supplier<IntContainer> supplier = () -> new BitSetContainer(Byte.SIZE);

var unique = lines
        .mapToInt(converter)
        .collect(supplier, IntContainer::add, IntContainer::addAll)
        .countUnique();

Мы получили простой и гибкий код, где, меняя реализацию контейнера, можно оптимизировать программу для разных вариантов входных данных. И хотя по сравнению с самым первым “наивным” подходом код стал сложнее, мы сократили требования к памяти и ресурсам процессора более, чем в десять раз.

Полный код доступен в репозитории по адресу:
https://github.com/rabestro/unique-ip-addresses