Приветствую Вас, уважаемые Читатели! Сегодня я хочу поговорить о таком геометрическом понятии, как конгруэнтность. В повседневной жизни мы его не используем, ведь куда проще говорить о равенстве, чем о такой трудновыговариваемой конструкции. Однако, в математике между ними есть отличие. Давайте на примерах!
Для начала возьмем два отрезка. В графическом редакторе они у меня получились с помощью "копировать-вставить". Что мы можем сказать о них?
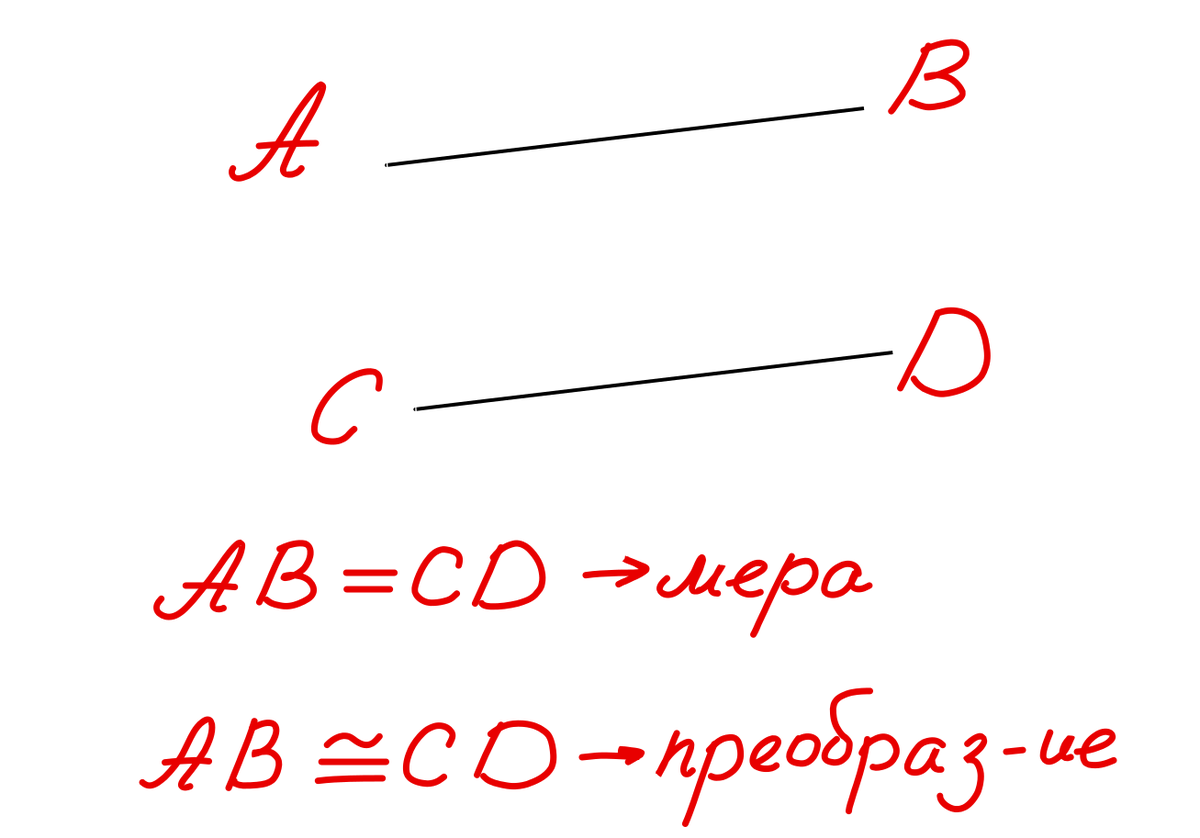
Когда мы говорим о "равенстве", мы предполагаем наличие некоторой меры, которая так или иначе сводится к числу. В нашем случае мерой является расстояние между точками или длина отрезка. В то же время мы можем говорить и о конгруэнтности отрезков, имея ввиду, что как геометрические фигуры (наборы точек) любой из отрезков можно получить из другого с помощью некоторого преобразования.
Например, в Евклидовой геометрии две фигуры называются конгруэнтными, если их можно взаимно получить из переноса, вращения и симметрии. Конгруэнтность определяется как отношение эквивалентности, обладающее свойствами рефлексивности, транзитивности и симметричности.
Теперь давайте перейдем к двумерным геометрическим фигурам. Очевидно, что треугольники, показанные на рисунке равны с точки зрения меры-площади и конгруэнтны, т.к. получены симметрией:

А что, если речь идёт о таком случае:

Здесь мера могла бы позволить нам говорить о равенстве площадей, но о конгруэнтности не может быть и речи. Однако же, если разрешить непрерывные деформации - сжатия и растяжения, все немного поменяется... В общем случае, конгруэнтность - это понятие, которое относится к теоретико-множественному представлению геометрических фигур. Апологетом этого подхода в СССР была знаменитый математик А.Н. Колмогоров.

Колмогоров вообще к определениям относился с большим вниманием. Например, категорически не любил понятие "равных" фигур (в том смысле, в котором его сейчас в школе используют), предпочитая определять их исключительно как "конгруэнтные". В качестве аргумента рисовал на доске два конгруэнтных треугольника А и B и говорил: "Ну как же эти фигуры могут быть равны? Если бы они были именно равны, то мы имели бы здесь A∩B = A = B. Это, очевидно, не так, ибо пересечение пусто A∩B = Ø!"

Этот подход, оказывается, применяется и в теории категорий, где можно отказаться от понятия равенства объектов, заменив их равенством т.н. стрелок между ними и введя понятие изоморфизма. Математика удивительна! Как здесь не вспомнить знаменитую фразу из Конституции США, написанной Томасом Джефферсоном: "Все люди равны между собой". Нет! Они создаются конгруэнтными. Они могут иметь равные права, но ни один человек не равен другому человеку.
Комментарии (14)

mayorovp
09.08.2022 15:27Что-то признаки равенства треугольников, как правило, называются именно признаками равенства, а не признаками конгруэнтности.

Sau
09.08.2022 16:00-2Теорию множеств тоже изучают, несмотря на то, что в ней присутствуют парадоксы (противоречия); далее её называют "наивная теория множеств".

StjarnornasFred
10.08.2022 10:32Наивная теория множеств - это всего лишь подмножество теории множеств (sic!). К тому же она уже более 100 лет как признана "непригодной для нужд математики" и нет смысла её рассматривать иначе как в историческом контексте.

pae174
09.08.2022 15:43+4Как здесь не вспомнить знаменитую фразу из Конституции США, написанной Томасом Джефферсоном: "Все люди равны между собой".
Это не из конституции а из декларации независимости. Фраза отдельно доставляет в связи с тем, что в тот момент вообще-то было рабство и всё такое. То есть люди, конечно, были равны. Просто некоторых за людей особо и не считали.

vassabi
09.08.2022 17:00насколько я знаю историю - всегда были варианты попасть в рабство или получить вольную. Есть ли такое место на Земле, где не было рабства?
В общем - это не неизменное состояние человека, а обстоятельства его жизни (я думаю, что наши потомки будут так же осуждать пожизненное заключение например)

Xobotun
09.08.2022 20:25+1Есть ли такое место на Земле, где не было рабства?
Пардон за бесполезный ответ, но полагаю, что как минимум Антарктида, из суши, и всё океанское дно, если по поверхности вообще.

vassabi
09.08.2022 22:41вот именно - только там где не было людей :)
PS: эх, жалко, что минуснувший не написал - что именно она\он не согласен в моем комментарии: с первым абзацем или со вторым ...
PPS: насколько я помню свой учебник древней истории из СССР, то рабство там описывалось как более прогрессивное поведение, по сравнению с принятым до рабства - т.к. охотой и собирательством прокормить удавалось только себя, то в плен чужаков никто не брал (а поступали как шимпанзе - убить и сьесть. Или просто убить). И только земледелие позволило гуманнее относиться к чужакам - оставлять их в живых (используя их подневольный труд для прокорма самого раба и его хозяина). Понятно, что более поздние времена - более сложные формы производства сделали подневольный труд настолько неэффективным, что сейчас в экономически развитых странах его используют разве что в тюрьмах ...

linuxoid
10.08.2022 07:52И даже это неверно, т.к. на океанском дне есть места, где таки были люди, правда дном оно тогда не было...

Solonchik
10.08.2022 20:23+1Пардон за бесполезный оффтопный ответ, но!
1) Джефферсон тащем-та вставил в Декларацию независимости и слова осуждения рабства, но по настоянию "кое-каких штатов" (не будем показывать пальцем) это упоминание вычеркнули из текста. Так что в его тексте с фразой "Мы исходим из той самоочевидной истины, что все люди созданы равными и наделены их Творцом определенными неотчуждаемыми правами, к числу которых относятся жизнь, свобода и стремление к счастью" - первоначально все было в порядке. Как вссегда, все испортила коллективная редактура - страшное зло, хоть в бизнес-процессах, хоть в творчестве.
2) Стыдливая изюминка в этой ситуации все-таки была. Потому что Вашингтон и Джефферсон на тот момент, насколько я помню, были примерно "плантатор намба уан" и "плантатор намба ту" по площади земель и по числу рабов, которыми владели. Вплоть до того, что Франция кредит новорожденным США выделяла под залог их земельных владений (даже если просрут, право частной собственности в Британии в тот момент более-менее священно). Отдельно доставляет, что Джефферсон еще и после смерти супруги прижил ребенка от темнокожей рабыни, но вольную ей так и не дал.
В общем, отцы-основатели США были ребята хоть куда.
P.S. Про саму же "Декларацию независимости" хоть пост пиши-кроши - интересно будет от всем, от историков до политтехнологов и пиарщиков и маркетологов IT-продуктов. Ее бы назвать "Как продать заведомо убыточный и социально токсичный продукт многомиллионным тиражом еще до релиза". Интереснейшая вещь, один из мощнейших и изящнейших пропагандистских документов в истории, который имел множество практических следствий и для Войны за Независимость США, и для современной истории. Но делать этого я, конечно же, не буду. Потому что там не только "право нации на самоопределение", но и "право нации на восстание против несправедливого правления", а я бутылочные средства не люблю ни внутрь, ни наружно.

Bronx
10.08.2022 06:58+2Конгруэнтность определяется как отношение эквивалентности, обладающее свойствами рефлексивности, транзитивности и симметричности.
А другие отношения эквивалентности этими свойствами не обладают, что-ли? Что за фигня тут написана?
Именно более общее отношение эквивалентности обладает этими тремя свойствами, а конгруэнтность — это всего лишь специальный случай для геометрических фигур. Непонятно, зачем ему уделена целая статья. Ради ссылки на Дзен?

e1vanov
10.08.2022 15:20Конгруэнтность встречается еще в нескольких разделах математики.
Дискретная математика
Опр. Функции алгебры логики
и
называются конгруэнтными, если одна получается из другой переименованием переменных. Например,
Эти функции не равны, поскольку,
, однако идейно делают одно и то же: возвращают значение одной из переменных независимо от другой.
Линейная алгебра
Опр. Матрицы
и
называются конгруэнтными, если существует такая невырожденная матрица
, что
.
Они используются для исследования квадратичных форм, например, для поиска преобразования координат, при котором уравнение формы примет наиболее простой вид: сама форма не меняется, меняется то, откуда мы на нее смотрим.

hoegni
11.08.2022 02:20Дело не в мере. Дело в том, что геометрическая фигура - это множество точек. А множества равны, если состоят из одних и тех же элементов. Очевидно, несовпадающие треугольники, даже если у них равны два углы и сторона между ними, состоят из разных точек, и, мледовательно, не являются равными множествами.Поскольку Колмогоров последовательно проводил концепцию, что математика основана на теории множеств, и внедрял эту идею в школьное образование, то для него это было важно. Ну и поскольку я учился в школе в "Колмогоровское" время, то для меня - тоже.

18741878
11.08.2022 12:13+1Я, конечно, дико извиняюсь - фотографию Курта Геделя на кой вставили? Нет, я знаю, что Гедель при испытании на право получить гражданство США тщательно изучил Конституцию и нашел в ней логические нестыковки. О чем сообщил Эйнштейну, выступавшему поручителем. И Эйнштейн его умолял не распространяться об этом, пока не закончится процедура получения гражданства.
Ну так и напишите об этом! Вместо это - посылаете на свой телеграм-канал. Который почему-то именуете "Математика не для всех", хотя правильнее было "Математика не для вас".
Жалко - не могу отминусовать


zkutch
"Когда мы говорим о "равенстве", мы предполагаем наличие некоторой меры, которая так или иначе сводится к числу."Не надо быть так категоричным, это не всегда так. Можно говорить о равентсва без введения понятия меры. Примером можно взять равенство множеств базирующее на аксиоме экстенсиональности https://proofwiki.org/wiki/Definition:Set_Equality#Axiom_of_Extension