Это мой первый серьёзный пост на подобную тему. В первую очередь я хочу очертить суть данной статьи. Тут я не буду разбирать полностью тему о генерации случайных чисел самим компьютером, за исключением одного термина для понимания разницы между Генерацией истинно случайных чисел(ГСЧ) и генерацией псевдослучайных чисел (ГПСЧ). Тут мы больше поговорим об алгоритмах которые используют языки программирования для генерации случайных чисел, и о том, почему они не случайны и не могут быть таковыми. Эта статья предназначена для тех программистов, которые минимум уже освоили функцию генерирующую случайные числа в своем языке, и хотят понять глубже эту тему. Я считаю эта тема одна из самых важных и в какой то степени сложной. Случайные числа очень полезны в различного рода алгоритмах, и понимание того, как они работают, возможно в будущем помогут вам сделать, что-то невероятное или просто полезное. А в конце я покажу свою псевдо-удачную попытку изобрести свой генератор псевдослучайных чисел.
Почему генерация случайных чисел в функциях языков программирования Не случайна?
Начнем с того, что на первый взгляд, кажется, что сгенерированное какой либо функцией число - абсолютно случайно. Но на деле - это Псевдослучайное число. Почему же его называют псевдослучайным? Суть в том, что оно получается путем вычислений. И тут мы сталкиваемся с тем, что генерация истинно случайных чисел, по определению не может быть никак вычисленной. Из-за того, что во многих подобных функциях используются алгоритмы(чаще всего похожие, либо модифицирован один и тот же), они не могут считаться истинно случайными.
Как можно получить истинно случайное число?
Я решил внедрить этот вопрос для большего понимания темы. И тут нам таки стоит ненадолго обратиться к материалам из общего определения ГСЧ самим компьютером. Хоть я и хотел в данном посте не прибегать к различного рода мудрым терминам, ведь его я пишу для новичков в данной теме. Но в этой части такие термины появятся, и эта часть окажется наверное самой сложной в этом посте. И так возвращаясь к вопросу. Как мы понимаем, для того что бы получить Истинно случайное число, у нас не должно быть каких либо вычислений, не считая входные данные, которые не всегда обязательны. И тут мы понимаем, что нужно выйти за рамки компьютера, хоть и не далеко от этих рамок, возможно даже остаться на границе с ними. Я подвожу к тому, что нам нужны какие-нибудь данные или средства из Реального мира, к тому-же, что то хаотичное. Можно взять к примеру шум вентиляторов вашего ПК или тепловой шум вашего процессора. Но опять таки эти данные нам придется обработать для получения результата, что нам не подходит.
Но тут на помощь приходит определение Энтропия. Из википедии: Энтропия - широко используемый в естественных и точных науках термин (впервые введён в рамках термодинамики как функция состояния термодинамической системы), обозначающий меру необратимого рассеивания энергии или бесполезности энергии.
А если простыми словами, то это мера хаоса в какой-либо системе, где система - это почти что угодно, в том числе и ваш ПК, или даже вся Вселенная! Из этого нас интересует лишь лишь мера хаоса. Мы пришли к хаотичности, то что нам нужно. Из этого выплывает, что на основе этого, можно собрать некое устройство, которое называют: Источник энтропии, или же Поставщик энтропии. Из википедии: Источники энтропии - используются для накопления энтропии, с последующим получением из неё начального значения, необходимого генераторам истинно случайных чисел (ГСЧ) для формирования случайных чисел. Отличие от генератора псевдослучайных чисел (ГПСЧ) в том, что ГПСЧ использует единственное начальное значение, откуда и получается его псевдослучайность, а ГСЧ всегда формирует случайное число, имея в начале высококачественную случайную величину, предоставленную различными источниками энтропии.
Тут мы наконец-таки получили ответ на основной вопрос. Хоть эта часть вышла слишком большой, но это понимание необходимо, что бы понять, что обычным алгоритмом, программно, получить истинно случайное число - невозможно. Однако не стоит этого пугаться. В большинстве случаев псевдослучайных чисел хватает. До того момента, пока вы не разрабатываете какой-либо серьезный алгоритм, в котором нужны только самые чистые данные.
Какие алгоритмы и методы используют в языках программирования для ГПСЧ?
По данному вопросу я сразу вспоминаю, про метод "Фибоначчи с запаздываниями" который используется в классе Random на платформе .NET(C#). Опять прибегнем к википедии: Запаздывающие генераторы Фибоначчи — генераторы псевдослучайных чисел, также называемые аддитивными генераторами. Однако это лишь метод, который является основой для алгоритмов.
Что такое "Аддитивные генераторы" и зачем они?
Аддитивные генераторы генерируют вместо случайных битов, случайные слова. Звучит уже страшно, но это не так сложно. Для начала нам нужно какое либо значение для данного генератора, которое будет ключом. Зная это состояние, можно составить формулу для вычисления n-ого слова генератора:
Я понимаю, что с начала это далеко не все поймут, и даже довольно опытные люди. Но с опытом это придет само, когда это вам действительно пригодится за рамками теории. Проще говоря, это основная составляющая для построения других алгоритмов на основе этого метода.
Пока что это все, что вам необходимо знать об алгоритмах генерации псевдослучайных чисел в языках программирования. Далее идут лишь разновидности алгоритмов, которые в сути своей являются этими самыми Аддитивными генераторами.
Как создать свой алгоритм для генерации псевдослучайного числа?
По сути я это рассказал в предыдущем блоке, а точнее дал основу для этого. Однако во-первых метод аддитивных генераторов не единственный, а лишь самый распространенный. А во-вторых давайте отбросим все эти скучные, пока что не понятные, и пока что не нужные формулы и правила. Давайте добавим немного фантазии и логики и сделаем на коленке свой алгоритм для ГПСЧ!
Впервые когда я задумался о подобном, я не представлял как это можно сделать. Однако немного подумав, понял, что мне нужно, что-то непостоянное. Что-либо, что после подстановки в формулу алгоритма оно тут же бы изменило свое значение. Самое не постоянное, что у меня было, это - время. А именно его миллисекунды. Я думаю, многие уже поняли какая суть была у моего алгоритма.
Снизу представлен код моего алгоритма, я его написал на языке Python. Да, я знаю, что это не самый лучший язык для написания подобных алгоритмов в плане скорости, я бы мог написать подобный код на том-же с# или с++, которые куда быстрее и лучше подходят для реализации таких алгоритмов. Однако python более человеко понятный и на нем объяснять алгоритмы куда проще.
import datetime
def gen_random_int(first, second):
if not isinstance(first, int) or not isinstance(second, int): # проверка на тип
raise ValueError("First value and secod value must be int type")
date_now = str(datetime.datetime.now())[-6:] # Выбираем из даты милисекунды
integer_for_gen = int(date_now + date_now) # Приводим милисекунды к типу int и добавляем к строке еще цифрроке
generated = 0 # Переменная для сгенерированного числа
while(True):
if generated >= first and generated <= second: # если в нашем диапозоне, прерываем цикл
break
elif first == second: # Если числа одинаковые, просто возвращаем первое или второе, не важно.
return first
integer_for_gen /= 17 # делим наши млсекунды на 17
generated = integer_for_gen # Присваиваем
return int(round(generated)) # Приводим к int для отброса дробной части, округляем и возвращаем
def main():
print(gen_random_int(2, 100))
if __name__ == "__main__":
main()Представленный алгоритм, ничто иное, как один из моих старых экспериментов. Он отлично работает с маленькими значениями, или значениями в которых разрыв между первым и вторым значение не большой. Однако я понимаю, что этот алгоритм не жизнеспособен, он далек от генерации даже псевдослучайных чисел, однако все таки числа полученные из него таки выглядят случайными. Я крайне не советую использовать такой алгоритм в реальных условиях, по крайне мене не в таком виде. Ибо при больших разрывах в значениях(200.000 и больше) Вы там вряд-ли увидите однозначные и даже 4-ехзначные числа. Но это был не плохой, маленький опыт. Отчасти у меня получилось сделать задуманное, поэтому в названии я написал "Псевдо-получилось".
Так-же можно путем таких экспериментов создать свой алгоритм, со своими уникальными данными. Это вовсе не сложно.
Итоги
После прочтения этой статьи, вы узнали, о том как работает генерация "случайных" чисел в вашем языке программирования(не важно какой это язык), и что они вовсе не случайны. А так-же, вы получили основу для создания своих алгоритмов по генерации псевдослучайных чисел. Эта тема очень обширная и большая, ни в одной статье за раз ее пройти невозможно, про нее можно писать книги. Эта статья лишь стартовая линия к началу этой огромной темы, и я надеюсь она помогла вам разобраться в основах генерации псевдослучайных чисел в программировании и не только.
Комментарии (19)

panteleymonov
03.09.2022 11:45Нет необходимости в бесконечных циклах, достаточно взять счетчик миллисекунд и отфильтровать его через функцию, например через sin. Тригонометрические или другие функцию вычислимые из ряда можно заменить на этот самый ряд и упростить его.

randomsimplenumber
03.09.2022 13:37И что получилось в результате? Сила ГПСЧ в том, что даже зная n предыдущих чисел, невозможно вычислить n+1. Даже если алгоритм генерации известен.

ReadOnlySadUser
03.09.2022 14:12+2Не обязательно же требование. Если требуется просто получать последовательности обладающие некоторыми статистическими свойствами, то соббсно пофигу на состояние и его предсказуемость.

randomsimplenumber
03.09.2022 15:30Вот ряд с прекрасными статистическими свойствами: 1 2 3 4 5 6 .. Всё равномерно. Годится? ;)

ReadOnlySadUser
03.09.2022 15:32+1Вполне, если мы, например, тестируем функцию, которая считает статистику.

GospodinKolhoznik
04.09.2022 13:32Не все равномерно. Распределение дельты Xn - Xn-1 имеет явно выраженный пик в точке 1 и провал во всей остальной области.

panteleymonov
03.09.2022 16:29+1Сила ГПСЧ в том, что даже зная n предыдущих чисел, невозможно вычислить n+1
Вот это новость! А "Линейный конгруэнтный ГПСЧ" не считается? Стандартная формула, где n+1 вычисляется как раз от предыдущего n.
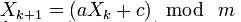
Ну и советую вам посмотреть примеры www.shadertoy.com, где основная функция для получения шума, среди прочих хешей, sin(n).

omxela
03.09.2022 21:43+1И хорошо бы дать ссылочку на известный труд Дональда Кнута, где описан конгруэнтный генератор, требования к нему, принципы создания, а также тесты, с помощью которых можно определить, "хороший" генератор или "плохой".

panteleymonov
04.09.2022 00:29Да, забыл пример своего варианта привести
https://onlinegdb.com/222WaynlG

kichrot
03.09.2022 15:17+3... Почему генерация случайных чисел в функциях языков программирования Не случайна? ...
Лично меня интересует иное, почему автор не дал определение понятия "случайность" прежде чем излагать это крайне безграмотное суждение???
Читаем научное определение:
СЛУЧАЙНОСТЬ – философская категория, выражающая один из предельных видов (классов) взаимосвязей и взаимоотношений в мире, характеризующийся отсутствием прямых закономерных связей в поведении и функционировании объектов и систем.
https://iphlib.ru/library/collection/newphilenc/document/HASHe582c0604b9932e6c8eae5
Как мы видим из определения, любое случайное событие является закономерным, но эта закономерность носит скрытый от наблюдателя характер, что создает у наблюдателя субъективное ощущение отсутствия закономерности.
По иному, понятие случайность определяют еще так:
Случайность, это непознанная закономерность.
Так, что любой генератор чисел, для наблюдателя незнающего его закономерность, генерирует всегда случайные числа.
Например, для наблюдателя незнакомому с арифметикой, генератор последовательности натуральных чисел от 0 до ထ , будет генерировать случайные числа. :)
Автор явно путает понятия "случайность" с понятиями "беспричинность" и "произвольность". :)

saaivs
03.09.2022 23:54+1Случайность, как непознанная закономерность - это очень смело, но с этим сложно согласиться.
Скорее случайность - это заведомое отсутствие закономерности.
Иначе вам придётся поставить под соменение основы современной квантовой механики. И страшного в этом ничего нет, т.к. постулироваие случайности базовых процессов физики даёт весьма интересные результаты.
А вот то, что это отчасти философская категория - согласиться можно. Но тоже с оговоркой, поскольку случайности вполне можно дать как математическую так и физическую интерпритацию.

GospodinKolhoznik
04.09.2022 13:40Однако, если этот наблюдатель не знающий арифметику попросит вас нарисовать график вашей случайной последовательности он скажет "я вижу явную закономерность".
На этом палятся многие ГПСЧ, что на их графиках зачастую можно увидеть рисунки-паттерны.

kichrot
04.09.2022 18:57Однако, если этот наблюдатель не знающий арифметику попросит вас нарисовать график вашей случайной последовательности он скажет "я вижу явную закономерность".
...
Совершенно верно. :)
Любой хаос обладает этим свойством - если наблюдатель, не знающий закономерность данного хаоса, попросит, знающего закономерность данного хаоса, нарисовать график закономерности данного хаоса, он скажет "я вижу явную закономерность". :)
Случайность, это непознанная закономерность.
Кстати, понятие "неопределенность", которым пытаются козырять невежественные "любители" квантовой теории, также указывает на непознанную закономерность:
НЕОПРЕДЕЛЕННОСТЬ - неполнота определяющих факторов.
Идеографический словарь русского языка. — М.: Издательство ЭТС. Баранов О.С.. 1995
Именно по этой причине в квантовой теории, в отношении принципа неопределенности Гейзенберга, преобладает интерпретация, в виде теории скрытых параметров. Т.е. мы в очередной раз видим, что случайность, это непознанная закономерность. :)

Politura
03.09.2022 22:51+4Одна из нужных фич широко используемых ГПСЧ - для одного и того-же значения seed, всегда получаем одну и ту-же последовательность чисел, какой-бы длинной она нам не была-бы нужна.

saaivs
03.09.2022 23:40+2Всякий, кто питает слабость к арифметическим методам получения случайных чисел, грешен вне всяких сомнений.
Само собой, не совсем в тему о ГПСЧ, но "красивое":)

GospodinKolhoznik
04.09.2022 02:13обычным алгоритмом, программно, получить истинно случайное число - невозможно
Интуитивно вроде бы так чувствуется, но доказать не могу. Существует ли доказательство сего факта?

Refridgerator
04.09.2022 07:27Начать надо с того, как проверить случайное число на истинность и возможно ли это в принципе.

sergeyzorin
05.09.2022 14:25Очень замечательная функция. И обладает замечательным свойством.
Для любых A и B таких, что A <= 0 <= B, gen_random_int(A,B) = 0. В любое время года :)


randomsimplenumber
Никогда не интересовался генераторами Фибоначчи, но няп в той формуле сумма рекурсивно полученных значений, а у вас - цикл с делением на 17. Похоже что эта программа не от этой задачи ;)