21.10.2022 23:53
honyaki 14 6000 Источник

image


В численной линейной алгебре нас интересуют точное и эффективное решение задач и понимание чувствительности задач к возмущениям. К старту флагманского курса по Data Science делимся материалом от профессора Ника Хигэма о семи грехах линейной алгебры, из-за которых теряется точность/эффективность или информация о чувствительности [к возмущениям] оказывается недостоверной.


1. Обращение матрицы


На курсе линейной алгебры мы узнаём, что решение линейной системы$Ax = b$, состоящей из $n$ уравнений, содержащих $n$ неизвестных, можно записать в виде $x = A^{-1}b$, где $A^{-1}$ — обратная матрица. При этом не всегда подчёркивается, что случаев, когда следует вычислять $A^{-1}$, очень мало. На самом деле, ($n=1$) скалярную систему $7x = 21$ нельзя решить, вычислив $x = 7^{-1} \times 21$. Вместо этого лучше выполнить деление $x = 21/7$ [прим. ред. — мы помним, что 7 в минус первой степени — это одна седьмая единицы, и, конечно, помним о свойствах умножения и деления дробей. Возможно, здесь имеется в виду разница в подходе к вычислениям в контексте вычислительной машины]. В случае $n\times n$ быстрее и точнее будет решение линейной системы (методом Гаусса) путём выбора ведущего элемента столбца, а не обращения $A$, которое в любом случае потребует LU-разложения матрицы).


Случаи, когда требуется использовать $A^{-1}$, редки, но возможны, когда диагональные элементы обратной ковариационной матрицы являются значимыми величинами, а также в некоторых алгоритмах вычисления матричных функций.


2. Формирование перекрёстного произведения матриц $A^TA$


Решение линейной задачи наименьших квадратов $\min_x\| b - Ax \|_2$, где $A$ — матрица полного ранга $m\times n$, где $m\ge n$ удовлетворяет нормальным уравнениям $A^T\!A x = A^Tb$. Поэтому естественно сформировать симметричную положительно определённую матрицу $A^T\!A$ и решить нормальные уравнения с помощью разложения Холецкого. Хотя этот метод быстрый, он численно неустойчив при слабообусловленной $A$. В противоположность этому решение задачи наименьших квадратов с разложением QR матрицы всегда численно устойчиво.


Что не так с перекрёстным произведением матриц $A^T\!A$ (известным как матрица Грама)? Она возводит данные в квадрат, что может привести к потере информации в арифметике с плавающей точкой. Например, при


$A = \begin{bmatrix} 1 & 1 \\ \epsilon & 0 \end{bmatrix}, \quad 0 < \epsilon < \sqrt{u}, $


где $u$ — единичная ошибка округления для плавающей запятой, то


$A^T\!A = \begin{bmatrix} 1 + \epsilon^2 & 1 \\ 1 & 1 \end{bmatrix} $


является положительно определённой, но, так как $\epsilon^2<u$ в арифметике с плавающей точкой $1+\epsilon^2$ округляется до $1$, получается вырожденная


$\mathrm{f\kern.2ptl}( A^T\!A) = \begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix}$,


при этом информация в $\epsilon$ потеряна.


Другая проблема с перекрёстным произведением матриц заключается в том, что $2$ — нормальное число обусловленности $A^T\!A$ — является квадратом такового для $A$. Это приводит к численной нестабильности алгоритмов, которые работают с $A^T\!A$, если число обусловленности велико.


3. Неэффективный порядок действий при определении произведения матриц


Число действий при определении произведения матриц зависит от порядка его определения (если принять, что не все матрицы $n\times n$). Иными словами, умножение матриц ассоциативно, поэтому $A(BC) = (AB)C$. В общем случае число действий при определении произведения матриц зависит от того, где поставить скобки. Один порядок может быть намного лучше других, поэтому не следует просто оценивать произведение в фиксированном порядке слева направо или справа налево. Например, если $x$, $y$ и $z$ — $n$ — векторы, то $xy^Tz$ можно определить так:


  • $(xy^T)z$: внешнее произведение векторов с последующим матрично-векторным произведением, которое требует $O(n^2)$ операций, а
  • $x (y^Tz)$: скалярное произведение векторов с последующим масштабированием вектора требует всего $O(n)$ действий.

Словом, определение места скобок в матричном произведении $A_1A_2\dots A_k$ для минимизации числа действий — это сложная задача, но для многих случаев на практике хороший порядок определить легко.


4. Предположение, что матрица является положительно определённой


Симметричные положительно определённые матрицы (симметричные матрицы с положительными собственными значениями) широко распространены, в том числе, потому, что они возникают при решении многих задач минимизации. Однако матрица, которая должна быть положительно определённой, может не быть таковой по целому ряду причин. Отсутствие или несоответствие данных при формировании ковариационной или корреляционной матрицы может привести к потере определённости, а ошибки округления могут сделать крошечное положительное собственное значение отрицательным.


Определённость подразумевает, что:


  • диагональные элементы матрицы положительны;
  • $\det(A) > 0$;
  • $|a_{ij}| < \sqrt{a_{ii}a_{jj}}$ для всех $i \ne j$.

Тем не менее ни одно из этих условий, равно как и все условия в совокупности, не может гарантировать, что матрица имеет положительные собственные значения.


Лучший способ проверить определённость, который зачастую может потребоваться сам по себе — рассчёт разложения Холецкого. функция MATLAB chol возвращает сообщение об ошибке, если разложение не удалось. При этом может быть запрошен второй выходной аргумент, в этом случае ему задаётся номер этапа, на котором случилась неудача факторизации, или 0, если факторизация прошла успешно. В случае неудачи частично вычисленный фактор $R$ возвращается в первом аргументе, и его можно использовать, например, для вычисления направления отрицательной кривизны, как это необходимо для оптимизации.


Этот грех занимает первое место в «Семи грехах оптимизации портфеля» (Seven Sins in Portfolio Optimization) Шмельцера и Хаузера, поскольку в этом случае отрицательное собственное значение в ковариационной матрице может определять портфель с отрицательной дисперсией, обещая при этом условно высокие инвестиции без риска!


5. Неиспользование структуры матрицы


Один из фундаментальных постулатов численной линейной алгебры заключается в необходимости использовать любую структуру матрицы. Особенно важно использовать разреженность (матрица с большим количеством нулей), поскольку алгоритмы, предназначенные для плотных матриц, могут оказаться непрактичными для разреженных матриц из-за обширного заполнения (нули становятся ненулевыми). Вот два примера структур, которые можно использовать.


Для задач нахождения седловой точки матрицы являются симметрично неопределёнными и имеют вид:


$\notag C = \begin{bmatrix} A & B^T \\ B & 0 \end{bmatrix}, $


где $A$ является симметричной положительно определённой. Разработка числовых методов для решения $Cx = b$ с использовании блочной структуры и возможной разреженности $A$ и $B$ оказалась весьма трудоёмкой задачей. Ещё один пример — циркулянтная матрица:


$\notag C = \begin{bmatrix} c_1 & c_2 & \dots & c_n \\ c_n & c_1 & \dots & \vdots \\ \vdots & \ddots & \ddots & c_2 \\ c_2 & \dots & c_n & c_1 \\ \end{bmatrix}. $


Важное свойство циркулянтных матриц — диагонализируемость унитарной матрицей дискретного преобразования Фурье. При помощи этого свойства $Cx = v$ можно решить за $O(n \log_2n)$, а не $O(n^3)$ операций, что потребовалось бы при игнорировании циркулянтной структуры.


В идеале программное обеспечение линейной алгебры должно обнаруживать структуру в матрице и вызывать алгоритм, использующий эту структуру. Ярким примером такого мета-алгоритма в MATLAB является функция x = A\b с обратным слешем для решения $Ax = b$. Функция с обратным слешем проверяет, является ли данная матрица треугольной (или преобразованной треугольной) матрицей, верхней матрицей Хессенберга, симметричной или симметричной положительно определённой. После такой проверки применяется подходящий метод. При этом $A$ также может быть прямоугольной. При этом задача наименьших квадратов решается, если строк больше, чем столбцов, или недоопределённая система, если столбцов больше, чем строк.


6. Определение приближения вырожденности с помощью определителя



$n\times n$ матрица $A$ является невырожденной только при ненулевом детерминанте. Поэтому можно ожидать, что малое значение $\det(A)$ указывает на почти вырожденную матрицу. Однако размер $\det(A)$ ничего не говорит о вырожденности. Действительно, поскольку $\det(\alpha A) = \alpha^n \det(A)$, мы можем получить любое значение определителя, умножив его на скаляр $\alpha$, однако $\alpha A$ имеет приближение вырожденности не больше и не меньше, чем $A$ для $\alpha \ne 0$.


Ещё одно ограничение для определителя показано на примере двух матриц:


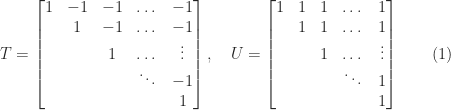
\notag T = \begin{bmatrix} 1 & -1 & -1 & \dots & -1\\ & 1 & -1 & \dots & -1\\ & & 1 & \dots & \vdots\\ & & & \ddots & -1 \\ & & & & 1 \end{bmatrix}, \quad U = \begin{bmatrix} 1 & 1 & 1 & \dots & 1\\ & 1 & 1 & \dots & 1\\ & & 1 & \dots & \vdots\\ & & & \ddots & 1 \\ & & & & 1 \end{bmatrix} \qquad (1)

В обеих матрицах есть единично диагональные и внедиагональные элементы, ограниченные по модулю $1$. Поэтому $\det(T) = \det(U) = 1$, но


$\notag T^{-1} = \begin{bmatrix} 1 & 1 & 2 & \dots & 2^{n-2}\\ & 1 & 1 & \dots & \vdots\\ & & 1 & \ddots & 2\\ & & & \ddots & 1 \\ & & & & 1 \end{bmatrix}, \quad U^{-1} = \begin{bmatrix} 1 & -1 & & & \\ & 1 & -1 & & \\ & & 1 & \ddots & \\ & & & \ddots & -1 \\ & & & & 1 \end{bmatrix}. $
Таким образом, $T$ является слабообусловленной для большого множества $n$. Фактически при изменении элемента $(n,1)$ матрицы $T$ до $-2^{n-2}$ матрица становится вырожденной! В противоположность этому $U$ всегда хорошо обусловлена. Определитель не позволяет отличить слабообусловленную $T$ от хорошо обусловленной $U$.


7. Определение обусловленности при помощи собственных значений


Для любой $n\times n$ матрицы $A$ и любой нормы согласованной матрицы справедливо, что $\|A\| \ge |\lambda_i|$ для всех $i$, где $\lambda_i$ являются собственными значениями $A$. Поскольку собственные значения $A^{-1}$ — это $\lambda^{-1}$, число обусловленности матрицы $\kappa(A) = \|A\| \, \|A^{-1}\|$ ограничено снизу отношением наибольшего собственному значению к наименьшему по абсолютной величине, т. е.:


$\notag \kappa(A) \ge \displaystyle\frac{ \max_i |\lambda_i| } { \min_i |\lambda_i| }. $


Но, как показала матрица $T$ в (1), эта связь может быть очень слабой.


Число обусловленности характеризует вырожденные, а не собственные значения 2-нормальной матрицы. В частности


$\notag \kappa_2(A) = \displaystyle\frac{\sigma_1}{\sigma_n}, $


где $A = U\Sigma V^T$ — сингулярное разложение матрицы с $U$ и $V$ ортогональностью и $\Sigma = \mathrm{diag}(\sigma_i)$, $\sigma_1 \ge \sigma_2 \ge \cdots \ge \sigma_n \ge 0$. Если $A$ симметрична, то, например, множества $\{ |\lambda_i| \}$ и $\{\sigma_i \}$ идентичны, но в целом собственные $\lambda_i$ и вырожденные $\sigma_i$ значения могут заметно различаться.


А мы разобраться с математикой, чтобы вы прокачали карьеру или стали востребованным IT-специалистом:



Чтобы посмотреть все курсы, кликните по баннеру:



Краткий каталог курсов

Data Science и Machine Learning



Python, веб-разработка



Мобильная разработка



Java и C#



От основ — в глубину



А также


Комментарии (14)


  1. fire64
    22.10.2022 00:38
    #24841156

    Очень интересно, но ничего непонятно.

    Спасибо за статью, к сожалению слабость математического аппарата, не позволяет оценить всю красоту статьи, но все равно спасибо.


  1. AAngstrom
    22.10.2022 04:08
    #24841336
    +13

    По поводу пункта 1: извините, но как же задолбала эта хрень, распространяемая людьми скорее по привычке, чем от каких-то тайных знаний. Во-первых, утверждение "решать систему уравнений методом Гаусса проще, чем делать LU-разложение" -- это какой-то логический парадокс. Стандартный метод LU-разложения (например в LAPACK'е) -- это и есть метод Гаусса. Во-вторых, обращение матрицы -- это решение системы уравнений с правой частью равной единичной матрице. Поэтому, в-третьих, если матрица А не является почти вырожденной, а правая часть не отличается на много порядков от единичной матрицы, нет никакой разницы, решаете ли вы систему уравнений или сначала считаете обратную матрицу, а затем умножаете на правую часть. В-четвёртых, бывают ситуации, когда нужна именно обратная матрица, которая является конечным результатом, и тогда смотри пункт 2.

    Не знаю, может и были когда-то времена, когда обратную матрицу считали методом Крамера (или бог его знает, какими ещё методами), и кто-то мудрый возвестил, что вместо обращения матрицы надо решать систему линейных уравнений, но в нынешнее время эти задачи решаются эквивалентными методами, и нет никакой разницы, как именно получать численное решение системы уравнений Ax = B.


    1. domix32
      22.10.2022 16:12
      #24842126

      которое в любом случае потребует LU-разложения матрицы

      не знаю где вы увидели "проще, чем LU-разложение"


    1. masai
      22.10.2022 17:23
      #24842236

      Во-первых, утверждение "решать систему уравнений методом Гаусса проще,
      чем делать LU-разложение" -- это какой-то логический парадокс.
      Стандартный метод LU-разложения (например в LAPACK'е) -- это и есть
      метод Гаусса

      Такого утверждения нет, виноват кривой перевод. В оригинале было: «it is faster and more accurate to solve a linear system by LU factorization (Gaussian elimination) with partial pivoting than by inverting A (which has, in any case, to be done by LU factorization)».

      Во-вторых, обращение матрицы -- это решение системы уравнений с правой частью равной единичной матрице.

      В статье речь идёт о системе, где правая часть — вектор. С точки зрения количества вычислений есть разница между решением системы, у которой правая часть матрица, и системы, у которой правая часть — вектор.

      нет никакой разницы, решаете ли вы систему уравнений или сначала считаете обратную матрицу, а затем умножаете на правую часть

      На практике разница есть. Я ради интереса попробовал решить систему с матрицей 10000x10000 на своём ноутбуке. Обращение матрицы с умножением в среднем заняло 20 с, а решение системы напрямую — в среднем 5 с. Так что разница очень даже ощутимая.


      1. AAngstrom
        22.10.2022 19:52
        #24842468

        Если в правой части вектор, то понятно, что решать систему просто быстрее, но вся эта телега про "решайте систему, а не инвертируйте матрицу" обычно также повторяется для случая, когда в правой части стоит матрица. И аргументы идут именно как раз в духе того отрывка, что Вы привели: "it is faster and more accurate to solve a linear system than by inverting". Да, оно может быть "faster" (максимум в 4 раза по умножениям), но только в случае вектора в правой части, а про "more accurate" я как раз и писал, что это не так, кроме клинических случаев, в которых в любом случае LU-разложение не подходит.

        Меня это задело, потому что я регулярно встречаю на форумах эти "лекции" (как правило вместо ответа на соврешенно другой вопрос) на тему того, как это плохо обращать матрицу, вместо этого надо решать систему уравнений. Но если в правой части тоже матрица, то просто так, в общем, нельзя сказать, что лучше. Выбор метода должен зависеть от того, что конкретно нужно посчитать, и нередко оказывается, что лучше сначала инвертировать матрицу.


        1. masai
          22.10.2022 22:11
          #24842710

          Я понимаю. Лишь хотел заметить ради справедливости, что эта статья всё же ничего такого криминального не утверждает.


          1. AAngstrom
            22.10.2022 22:33
            #24842768

            На самом деле, Хайэм -- крутой вычматист (приходилось разбираться в его статьях по интерполяции), и если отбросить пункт 1, то на остальные пункты (особенно 2, 5, 6 7) действительно стоит обратить внимание.


  1. sunnybear
    22.10.2022 06:32
    #24841418
    +2

    "При этом задача наименьших квадратов решается, если строк больше, чем столбцов, или недоопределённая система, если столбцов больше, чем строк." -> "При этом, если строк больше, чем столбцов, то решение ищется по методу наименьших квадратов. А если столбцов больше, чем строк, то решается задача недоопределенной системы."


  1. N-Cube
    22.10.2022 08:04
    #24841480
    +8

    Просто адский гуглотранслейт, читать невозможно. Для практического использования все базовые алгоритмы реализованы в библиотеках и там же сделаны необходимые проверки на вырожденность матриц и прочее, а вот частные случаи чтобы решить, нужно знать теорию. Например, в библиотеке Python numpy предлагается реализация алгоритма наименьших квадратов (МНК), но нет взвешенного МНК, который часто бывает нужен. К счастью, это легко обходится с помощью нормирующей матрицы (которая постоянно нужна для реальных задач, но в статье выше о ней вообще не упомянули) - легко, при определенных ограничениях на коэффициенты. К примеру, я об этом писал в статье на хабре «Линейная алгебра для спутниковой интерферометрии» https://habr.com/ru/post/597227/


  1. Codenamed
    22.10.2022 11:32
    #24841730
    +5

    Я понимаю, что это перевод, но уж если вы переводите специализированную статью для широкой аудитории, то стоило хотя бы не самые базовые определения, вроде обусловленности, привести в начале статьи или в соответствующей части. А то это неуважение к аудитории просто.


  1. thevlad
    22.10.2022 18:02
    #24842292

    Еще бы хорошо, написать про регуляризацию, когда на практике, если матрица может быть вырождена, заместо: M*b=a, стоит решать min ||M*b - a|| (если система имеет хотя бы одно решение, то будет 0, иначе ближайшая точка), (псевдо-инверсии тоже из этой оперы)


  1. homocomputeris
    22.10.2022 20:46
    #24842566
    +1

    Ника Хигэма

    ААААААА

    перекрёстного произведения

    Это шо за зверь?

    определении произведения матриц

    Называется "вычисление".


  1. omxela
    22.10.2022 21:53
    #24842674

    Библиотеки, конечно, хорошо. Но тот, кто использует численные методы, знает, что каждая задача особенная в том или ином смысле. Эти особенности могут испортить жизнь при стандартном подходе. С другой стороны, они же могут позволить что-то улучшить и ускорить, иногда существенно. По всем вопросам, затронутым в статье, есть давняя и обширная литература. Помню, на меня сильное впечатление произвела книжка Форсайта-Малькольма-Моулера "Машинные методы математических вычислений" издательства МИР 1980 г.


  1. AndrewSu
    22.10.2022 22:10
    #24842708

    В противоположность этому решение задачи наименьших квадратов с разложением QR матрицы всегда численно устойчиво.

    Очень сильные сомнения в верности этого утверждения.