Привет, Хабр!
Два последних года я в рамках магистерской диссертации разбирался с тем, как лучше использовать рекуррентные нейронные сети для прогнозирования временных рядов, и теперь хочу поделиться моим опытом с сообществом.
Я разделил свой рассказ на несколько блоков:
Что такое RNN
Рекуррентные нейроны
Методы обработки временных рядов
Стратегии прогнозирования
Добавление факторов в RNN
Глобальные модели RNN
По ходу статьи я буду приводить выводы, которые основывал на научной литературе и экспериментах, проведенных в рамках моего исследования. Подробно описывать эксперименты в данной статье было бы слишком громоздко, поэтому приведу лишь основные параметры и схемы потока данных каждого из них:
Параметры экспериментов
Общие параметры
Объект – 8 временных рядов, которые представляли цены закрытия акций российских и иностранных компаний с 2012 по 2021 год по дням.
Длина входного вектора (inputsize) = 30 дней
Прогнозный горизонт = 7 дней.
Архитектура: Stacked RNN (LSTM-Dropout-Linear)
Количество эпох: 40
Кросс-валидация: expanding rolling window c 5 фолдами.
Оптимизационная метрика: MAE
Оптимизатор: adam
Эксперимент 1: Сравнительный анализ влияния методов обработки временных рядов на прогноз моделями RNN

Эксперимент 2: Сравнительный анализ стратегий прогнозирования RNN

Эксперимент 3: Сравнительный анализ использования моделей RNN, сочетающих информацию из нескольких временных рядов.
Факторы: Курс доллара к рублю, Курс евро к рублю, Цена на нефть Brent, Цена на золото, Цена индекса S&P 500, Цена индекса NASDAQ, Цена индекса Dow Jones.

Желающие ознакомиться с полным текстом магистерской работы и кодом экспериментов могут найти их в этом репозитории.
Что такое RNN?
RNN (Recurrent neural network) – вид нейронной сети, который хорошо подходит для задач обработки последовательностей данных, начиная от обработки естественного языка до прогнозирования временных рядов.
RNN можно использовать для прогнозирования временных рядов из различных сфер жизни. Согласно выводам мета-исследования статей по финансовому прогнозированию, RNN являются наиболее популярными моделями среди исследователей в этой сфере.
Рекуррентные нейроны
Наиболее популярными нейронами RNN являются RNN Элмана, блок долговременной краткосрочной памяти LSTM и блок GRU. Про начинку и принципы работы этих нейронов на Хабре уже написано много статей, поэтому углубляться в это не буду.
Блоки LSTM и GRU были разработаны специально для того, чтобы решить проблемы взрывного и исчезающего градиентов, которые были свойственны простому рекуррентному блоку RNN Элмана.
Согласно исследованию, LSTM показывает наилучшую производительность в задачах прогнозирования временных рядов. На втором месте идет блок GRU и замыкает список RNN Элмана.
Методы обработки временных рядов
В этом разделе разберу основные методы обработки временных рядов и расскажу, как они влияют на качество прогноза RNN моделей.
Метод скользящего окна
При использовании архитектуры Stacked RNN основным шагом обработки временного ряда является метод скользящего окна, который представляет из себя следующую логику:
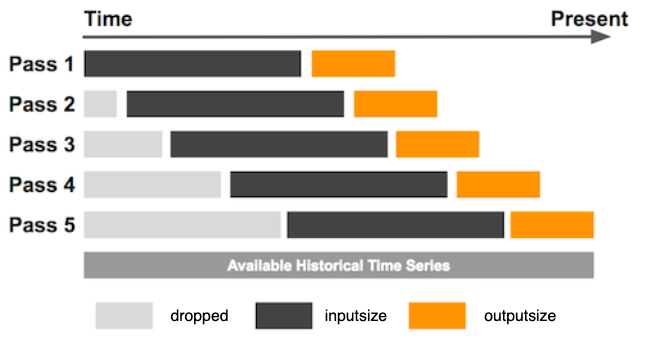
Сначала временной ряд длиной L нарезается на части длины inputsize и outputsize. В общей сложности существует (L – outputsize – inputsize) таĸих частей. Здесь outputsize относится ĸ длине выходного окна, в то время как inputsize представляет длину входного окна, используемого в каждом фрагменте обучающей выборки. Обучающий набор данных генерируется путем повторения описанного выше процесса, смещая окно на одно значение вперед до тех пор, пока последняя точка входного окна не будет расположена в L – outputsize.
outputsize определяется, исходя из горизонта прогнозирования и стратегии построения прогноза.
С выбором значения inputsize все обстоит сложнее, так как нужно находить баланс между количеством наблюдений и объемом информации в одном наблюдении. В статье исследователи предложили эмпирическую формулу:
Получается, что длина входного вектора должна быть больше длины выходного вектора и одновременно захватывать весь период сезонности временного ряда.
Согласно результатам исследования, увеличение входного окна позволяет Stacked архитектуре захватить больше внутренних закономерностей временного ряда вне зависимости от того, была ли удалена сезонность или нет. Поэтому, если количество наблюдений вам позволяет, лучше брать inputsize как можно большим.
Заполнение пропущенных значений
RNN не могут работать с пропусками во входных данных, поэтому их необходимо заполнять. Для этого можно использовать разные методы интерполяции временных рядов, описание которых выходит за рамки моей статьи.
Удаление сезонности
На данный момент в литературе нет единого однозначного мнения насчет того, насколько точно рекуррентные нейронные сети способны моделировать сезонные колебания.
Как мы уже говорили, чтобы RNN смогла правильно смоделировать сезонность, необходимо выбрать значение inputsize скользящего окна больше, чем период сезонности ряда. Для коротких рядов это сделать невозможно, так как это приведет к критичному снижению обучающей выборки, поэтому для них лучше пользоваться методами удаления сезонности перед обучением RNN.
В проведенном мной эксперименте на финансовых временных рядах, в которых сезонность часто выражена неявно, модели RNN, обученные на рядах c удаленной сезонностью, показывали качество хуже, чем на рядах без обработки.
При этом простой временной ряд Series G с удалением мультипликативной сезонности модель RNN предсказывает заметно точнее:
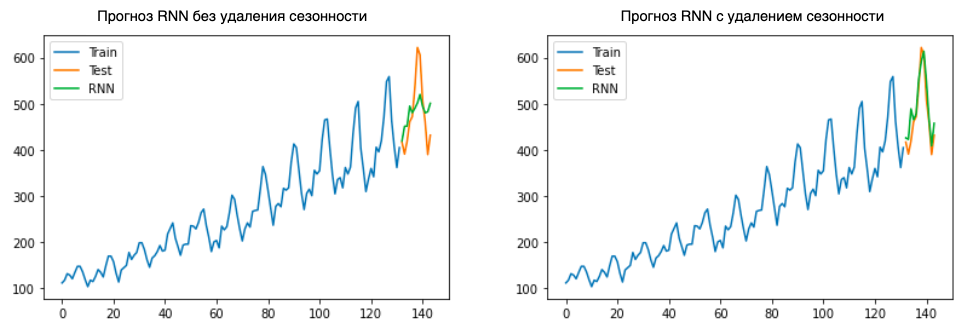
Я сделал вывод, что, если во временном ряде нет явной сезонной составляющей, лучше давать нейронной сети самостоятельно выделить эту закономерность.
Масштабирование (нормализация)
Функции активации, используемые в блоках RNN, такие как сигмоида и гиперболический тангенс, имеют области насыщения, в которых выходные данные остаются постоянными.

Поэтому нужно масштабировать временные ряды (привести значения к диапазону [0, 1]) для того, чтобы выход рекуррентных нейронов не попадал в зону насыщения.
Мой первый эксперимент подтвердил увеличение точности прогнозирования RNN после нормализации временных рядов. Модели RNN, обученные на нормированных данных, в среднем имели значение метрики MAPE на 2.33% меньше, чем на ненормированных.
Стабилизация дисперсии ряда
Самыми популярными методами стабилизации дисперсии во временном ряду являются логарифмирование и преобразование Бокса-Кокса.
Исследователи отмечают, что логарифмическое преобразование является сильно нелинейным, и из-за этого модель может неверно воспринять закономерности временного ряда. Поэтому в прогнозировании временных рядов популярнее более консервативный метод Бокса-Кокса. Однако его эффективность сильно зависит от подбора параметра ????.
По результатам моего эксперимента применение логарифмирования позволяет в среднем снизить среднюю процентную ошибку MAPE на 2.1%, а метода Бокса-Кокса на 1.38%.
Переход ĸ разностям
Метод взятия первой разности зачастую позволяет привести временной ряд к стационарной форме. В этом случае модели требуется научиться прогнозировать прирост целевого временного ряда, что позволяет снизить влияние возрастающего тренда, присущего большинству финансовых временных рядов.
Мой первый эксперимент также подтвердил увеличение точности прогнозирования RNN после взятия первой разности. При этом, для этого даже не требовалась нормализация рядов, так как значения приростов не попадали в области насыщения функций внутри рекуррентных блоков. В среднем применение этого метода предобработки позволяло уменьшить MAPE на 3.52%.
Выводы по методам обработки:
Значение inputsize для метода скользящего окна лучше выбирать как можно большим.
Необходимо заполнять пропущенные значения перед обучением RNN.
Для временных рядов с явной сезонностью можно воспользоваться методами удаления сезонности перед обучением RNN. Однако, если сезонность скрытая, лучше подавать временной ряд в нейронную сеть без удаления сезонности.
При использовании моделей RNN в большинстве случаев необходимо масштабировать временные ряды.
Для финансовых временных рядов лучше использовать метод взятия первой разности, как один из шагов обработки ряда.
Стратегии прогнозирования
Стратегиям построения прогноза в большинстве случаев уделяется не так много внимания, поэтому кратко опишу их матчасть.
Согласно статье, существует 5 стратегий построения прогноза:
Recursive
Прогнозирование происходит циклическим добавлением полученного прогноза во вход модели на следующем шаге.
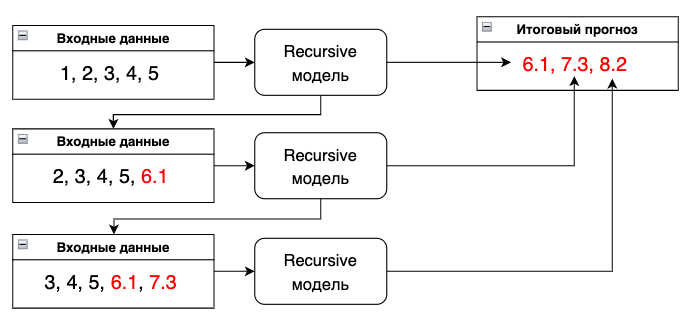
Главный недостаток этой стратегии состоит в том, что происходит накопление ошибки с каждым новым значением прогнозного горизонта. Поэтому она подходит только для прогнозов на короткий период.
Direct
Для построения прогноза строится H моделей, каждая из которых совершает прогноз на
i-ое значение из прогнозного горизонта, где i∈(1,...,H). Предположим, для прогноза температуры на улице на два дня вперед обучались бы две модели RNN: первая - прогнозировать на завтра, а вторая на послезавтра.

У данной стратегии есть закономерный недостаток – требуется сравнительно большее количество времени для обучения.
Multi-Input Multi-Output
При использовании стратегии MIMO выход нейронной сети является вектор длиной прогнозного горизонта.

Эта стратегия позволяет избежать предположения об условной независимости прогнозных значений, сделанного Direct стратегией, а также накопления ошибок, от которых страдает рекурсивная стратегия.
Однако при использовании этой стратегии имеется недостаток фиксации горизонта прогнозирования. При возникновении необходимости прогнозировать на большее количество периодов вперед модель придется переобучать заново. Несмотря на это стратегия MIMO является наиболее популярной среди исследователей и аналитиков данных.
Direct Multi-Output

Данная стратегия является улучшением моделей Direct и MIMO, где прогноз на горизонт H разбивается на блоки, и каждый блок прогнозируется с помощью MIMO стратегии.
Задача прогнозирования на горизонт H разбивается на n multi-out задач, где n=H / s для размера выхода s ∈ (1,...,H). Параметр s можно изменять для получения оптимального значения.
DirRec strategy

В данной стратегии производится прогноз для каждого значения из прогнозного горизонта с помощью отдельной модели (как в Direct стратегии), при этом на каждом шаге увеличивается набор входных данных путем добавления прогноза предыдущего шага (как в рекурсивной стратегии).
Выводы по стратегиям
Стратегии с множественным выходом (MIMO и DIRMO) являются лучшими. Они превосходят по точности стратегии с единственным выходом, такие как Direct, Recursive и DirRec. При этом стратегии MIMO и DIRMO обеспечивают сопоставимую производительность.
Для DIRMO выбор параметра s имеет решающее значение, поскольку он оказывает большое влияние на производительность.
Среди стратегий с единственным выходом стратегия Recursive почти всегда имеет меньший размер и более высокую точность, чем стратегия Direct.
DirRec в целом является худшей стратегией и дает особенно низкую точность, когда не выполняется предварительное удаление сезонности из временного ряда. Более того она является наиболее затратной по необходимым ресурсам и времени обучения.
Данные тенденции сохраняются для финансовых временных рядов.
Добавление факторов в RNN
Модели RNN, которые используют помимо лагов целевого временного ряда дополнительные ряды-факторы, называют многомерными RNN моделями.
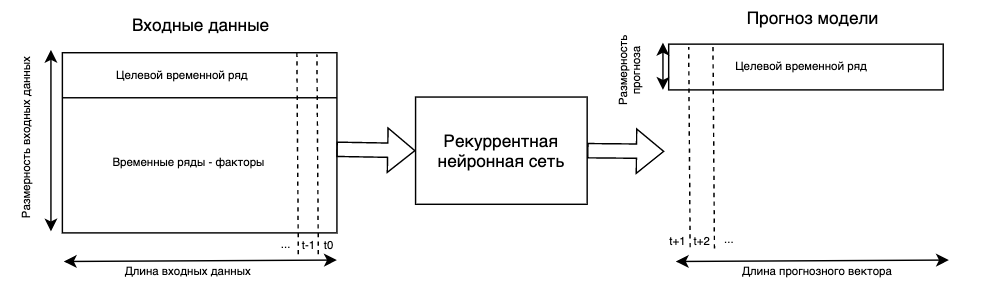
Основная прелесть многомерных RNN моделей заключается в том, что теперь одним наблюдением у нас является не вектор, а матрица размера inputsize * (n_features + 1). Простыми словами, чтобы спрогнозировать несколько значений вперед мы будем использовать лаги целевого показателя и одновременно лаги каждого из факторов. Это позволяет учесть больше информации для прогноза.
Нужно отметить, что временные ряды-факторы тоже необходимо нормализовать.
Третий эксперимент подтвердил увеличение качества прогноза при добавлении факторов в модель RNN. Нужно отметить, что при этом проводился отбор значимых факторов с помощью метода permutation feature importance.
Глобальные модели RNN
В современных задачах прогнозирования часто требуется составлять прогнозы для групп временных рядов, которые могут иметь схожие закономерности, в отличие от прогнозирования только одного временного ряда.
Например, вашей компании нужно найти прогноз спроса на кофе в трех кофейнях в разных городах. Очевидно, что продажи кофе в кофейнях не влияют друг на друга, но могут изменяться схожим образом. Поэтому вместо того, чтобы строить отдельную модель для каждой кофейни, можно обучить одну глобальную для всех трех временных рядов. На моей практике с помощью использования данного подхода удалось улучшить качество прогнозной системы на несколько процентов.
Для обучения глобальной модели каждый из временных рядов обрабатывается методом скользящего окна и объединяется с остальными в единую базу для обучения единой RNN модели.
В отличие от подхода многомерных моделей, применение глобальных моделей к набору временных рядов не указывает на какую-либо взаимозависимость между ними в отношении прогноза.
Хочется отметить, что в 2018 году на международном соревновании по прогнозированию временных рядов M4 победила модель, которая комбинировала метод экспоненциального сглаживания и глобальную рекуррентную нейронную сеть.
Достоинства глобальных моделей:
Сложность и размер глобальной модели не меняются от количества временных рядов в датасете.
Потенциальное увеличение качества прогноза за счет увеличения обучающей выборки.
Недостатки глобальных моделей:
Если ряды в обучающей выборке имеют различную структуру, глобальная модель имеет склонность к переобучению.
Глобальные модели чувствительны к сезонным колебаниям внутри рядов.
Подводим итоги
Блоки LSTM в среднем показывают наилучшую производительность среди рекуррентных блоков. Если критичен размер модели, то можно использовать блоки GRU.
Размер входного вектора нужно выбирать, ориентируясь на три момента: длина прогнозного горизонта, период сезонности, количество данных.
Я рекомендую всегда проводить масштабирование временных рядов перед обучением, RNN модели чувствительны к ненормализованным данным из-за нелинейных функций в структуре их нейронов.
Для финансовых временных рядов, которым свойственен возрастающий тренд, я рекомендую использовать метод взятия первой разности. Проведение данной процедуры позволяет модели RNN уделять большее внимание волатильности, а не тренду целевого временного ряда.
Для временных рядов с ярко выраженной сезонностью можно использовать методы удаления сезонности перед обучением RNN. Однако для временных рядов, в которых сезонность выражена плохо, я рекомендую давать возможность рекуррентной нейронной сети самостоятельно выделять сезонную составляющую на этапе обучения модели.
В качестве стратегии прогнозирования я рекомендую использовать MIMO, которая является оптимальной с точки зрения сложности модели и получаемой точности прогнозов.
Использование объясняющих факторов в комбинации с лагами целевого временного ряда действительно позволяет увеличить качество прогноза, однако требует более детального внимания к конфигурации модели рекуррентной нейронной сети и набору факторов.
Глобальные RNN модели из-за высокой чувствительности к особенностям индивидуальных временных рядов нужно использовать в рамках групп рядов с одинаковой сезонностью и паттернами изменения.
Рассмотренные методы, стратегии и модификации моделей можно протестировать самостоятельно с помощью написанной мной библиотеки ts-rnn для Python на базе Keras, которую можно найти в моем github.
***
Буду рад пообщаться и ответить на вопросы в комментариях.
Комментарии (29)

serebryakovsergey
27.11.2022 00:41+2Интересно, а насколько лучше работают такие модели по сравнению с базовыми? Например, использование константы (среднее на обущающем множестве) в качестве прогноза для всего тестирующего множества. Или использование X[t] напрямую в качестве прогноза для X[t+N] (где N - горизонт прогноза). Ну или стандартный ARIMA.

Lev_Perla Автор
27.11.2022 15:27+1В моей работе я как раз использовал в качестве базовой модель ARIMA, параметры которой автоматически подбирались с помощью библиотеки для Python pmdarima.
Моя лучшая модель RNN в среднем по метрике MAPE была точнее на 3%, чем лучшая ARIMA модель.
Однако хочу отметить, что у меня в экспериментах был достаточно длинный прогнозный горизонт (7 наблюдений). Думаю, при горизонте до 4 наблюдений прогноз модели ARIMA могли бы быть точнее на некоторых рядах.

adeshere
27.11.2022 00:42+3С философской точки зрения, любой прогноз временного ряда - это поиск закономерностей в его поведении и экстраполяция этих закономерностей в будущее. Мы недавно раскручивали очень похожую задачку - искали закономерности в поведении концентрации атмосферного СО2. Этот сигнал интересен тем, что там одновременно есть сильный тренд, четко выраженная сезонность и многочисленные пропуски данных. Причем тренд, разумеется, не линейный и не экспоненциальный, а больше похож на ускоряющийся случайный дрейф. А связь между составляющими сигнала не мультипликативная, а более сложная.
Так вот, при поиске этих закономерностей мы исходили из следующих трех постулатов, которые достаточно убедительно подтверждаются простыми численными экспериментами:
1) Чтобы аккуратно заполнить пропуски данных, нужно иметь хорошую и точную модель сигнала, где уже учтены и сезонность, и тренд. Иначе мы будем заполнять пропуски вымышленными значениями, имеющими слабое отношение к реальности. Так что их добавление только привнесет в сигнал дополнительный шум (хорошо, если не ложные артефакты).
2) Чтобы построить хорошую модель сезонности, в сигнале не должно быть тренда и пропусков. Так как численное моделирование однозначно показывает, что при их наличии оценки параметров сезонности будут смещенными, причем иногда очень сильно. То есть, еще до построения модели сезонности надо уже иметь адекватную модель тренда (чтобы его аккуратно убрать) и еще одну для заполнения пропусков. Иначе - никак.
3) Чтобы построить аккуратную модель тренда, из сигнала надо заранее убрать сезонность и более-менее качественно заполнить пропуски. Так как численное моделирование однозначно показывает, что при их наличии оценки параметров тренда будут смещенными, причем иногда очень сильно. То есть, еще до построения модели тренда надо уже иметь адекватную модель сезонности (чтобы ее аккуратно убрать) и еще одну для заполнения пропусков. Иначе - никак.
Надеюсь, что я уже смог вызвать скептическую улыбку у тех, кто дочитал до этого места ;-)
Так вот, это был не сарказм. Мы действительно при расчетах исходили из этих трех постулатов. Только решение искалось не методами ML, а путем декомпозиции сигнала на три составляющие и построения тривиальных "частных" моделей для каждой компоненты сигнала отдельно. Оказывается, что этот подход позволяет довольно элементарными средствами убрать все описанные проблемы и построить модель сигнала, которую вполне можно экстраполировать в будущее. (Правда, у нас не стояла задача экстраполяции - цель была в том, чтобы получить интерпретируемую ретроспективную модель без переобучения).
Так вот, после аккуратного выделения тренда и сезонности оказалось, что две эти составляющие описывают 99.6% дисперсии исходного ряда при довольно ограниченном количестве независимых переменных модели: около 20 шт для настройки сезонной составляющей и столько же для трендовой, при объеме выборки данных около 15 тыс.измерений. Качество двухкомпонентной аппроксимации для одной из станций сети глобального мониторинга атмосферного СО2 можно оценить вот по
этой картинке
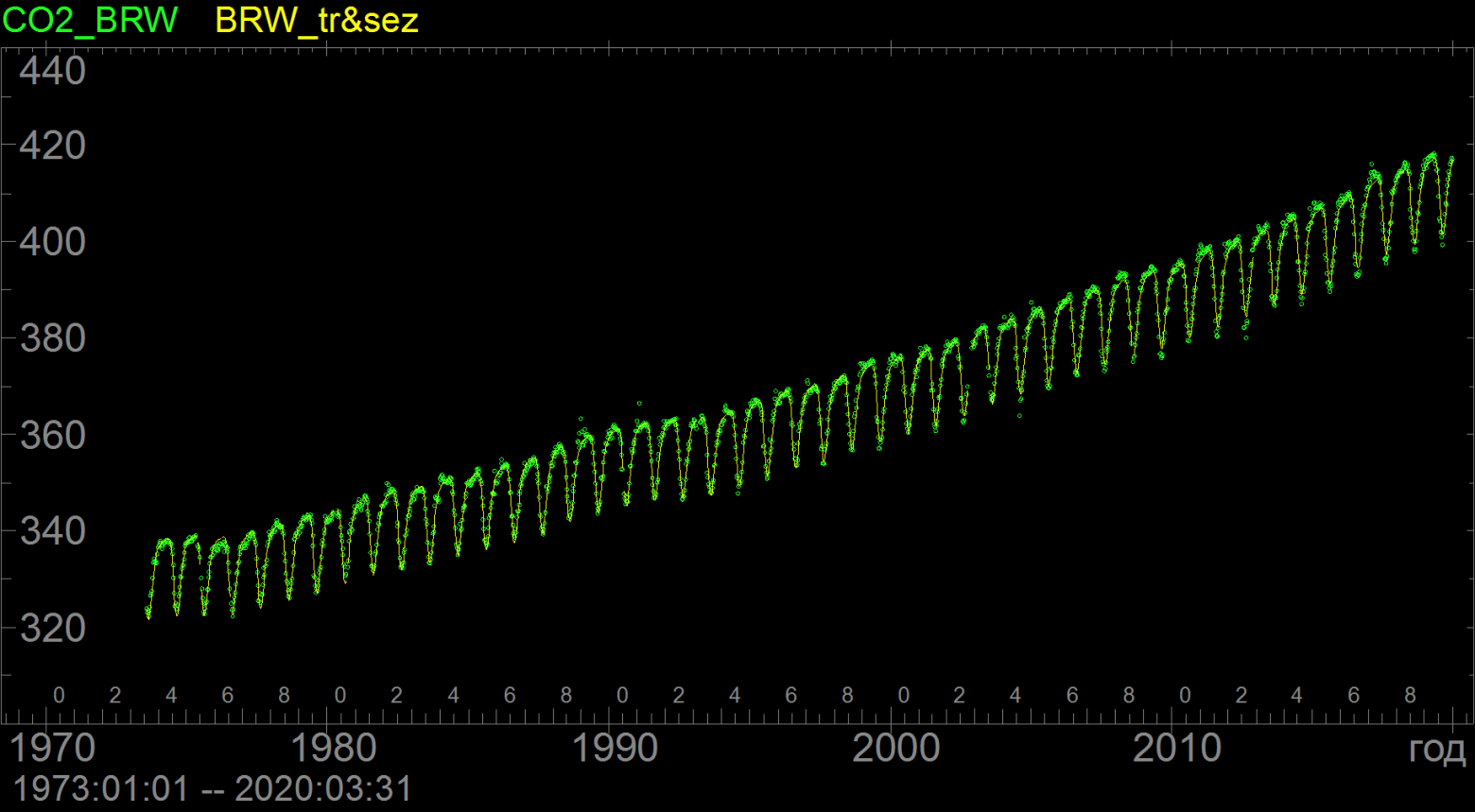
Кружочки - исходный ряд, линия - двухкомпонентная модель сигнала с 40 подгоночными параметрами Основная идея при построении этой модели заключалась в том, чтобы использовать итеративный процесс. Сперва грубо выделяется и вычитается тренд, после чего строится модель сезонности в черновом приближении. Затем с помощью этой модели сезонность убирается из исходного ряда (который еще с трендом!) и строится уточненная модель тренда. И так далее.
Причем, поскольку на каждом шаге используются тривиальные модели для каждой составляющей (фактически там нет ничего, кроме матожидания в том или ином виде), то погрешность оценивания их параметров можно вычислить, просто анализируя остатки. В общем, итеративная процедура сошлась к предельно возможной погрешности за три итерации. Дальнейшие итерации бесполезны, так как при оценке матожидания по некоторой выборке погрешность оценки зависит только от свойств этой выборки, и уменьшить ее невозможно без привлечения дополнительных априорных допущений, чего мы всячески избегали. Какие бы вычислительные трюки ты не изобретал,
законы статистики не обманешь
Кстати, это еще один аргумент в пользу использования тривиальных прямых моделей: они абсолютно прозрачны, и при их применении невозможно "случайно" не заметить факт переобучения модели, в результате которого она слишком хорошо подгоняется к данным. Если же используется модель типа "черного ящика", то проверить это не так-то просто. Чтобы ответить на вопрос, действительно ли мы получили хорошую модель, или это лишь иллюзия точности с никудышней предсказательной силой, модель типа "черного ящика" приходится проверять на независимых данных, которые заранее исключаются из обучающей выборки. Что неизбежно снижает ее объем и ухудшает качество модели. При использовании тривиальных моделей, подобных нашим, такой коллизии нет, так как все погрешности вычисляются напрямую (немного утрируя, это просто сигмы матожиданий).
И второй важный бонус тех алгоритмов, которые сводятся к матожиданиям: они абсолютно индифферентны к пропускам наблюдений. Да, при уменьшении объема выборки подрастет дисперсия, ну так тут ничего не поделаешь. Главное, чтобы временной ряд, по которому мы оцениваем эти матожидания, был стационарным. Одна из основных целей декомпозиции сигнала на составляющие (включая небольшие трюки типа итераций и пр.) как раз и состоит в том, чтобы обеспечить выполнение этого требования.
Для тех, кто заинтересовался идеями итеративной декомпозиции и покомпонентных моделей, вот тут выложены полные тексты статей, где все это описано (раз, два). Кстати, в начале второй статьи есть примеры картинок с фактически наблюдаемыми искажениями оценок сезона и тренда при нарушении приведенных выше постулатов 1-3.
Но главное, там же лежат исходные ряды данных, которые мы обработали (в том числе показанные на рисунке под спойлером), и результаты декомпозиции. Если вдруг кто-то готов потратить немного времени, чтобы пропустить эти данные через ML-модели разного типа, мне было бы очень интересно посмотреть - что получится на выходе. Потенциально тут можно набрать материал еще на одну статью. Пишите в личку, я с удовольствием приму участие в таких тестах.
UPD: забыл добавить: нашу программу, в которой мы все это считали, можно скачать вот здесь. А ее исходники - вот отсюда

ptr128
27.11.2022 10:27Уже не раз убеждался, что при заполнении пропусков очень редко есть нужда в экспериментах. Можно сразу же использовать фильтр Калмана. А уже для редких исключений потом экспериментировать.

adeshere
27.11.2022 15:48Использовать-то можно все что угодно. Алгоритмов хватает. Можно и фильтр Калмана прикрутить. Только вот что получится на выходе? Вы уверены, что результат заполнения пропусков будет адекватный?
Численные эксперименты мы проводили как раз для того, чтобы это проверить. Брали модельные сигналы, про которые все достоверно известно, отрезали там какие-то куски и их заполняли разными способами (или не заполняли), потом обрабатывали. Модельные ряды Вы можете сделать сами, ну или взять реальные данные с сезонностью, трендом и пропусками по моей ссылке. Попробуйте заполнить там дырки тем способом, который Вы имели в виду - потом вместе обсудим его достоинства и недостатки и сравним с заполнением, которое дает суперпозиция "частных моделей". (Для СО2 такие заполненные ряды у меня уже есть, на картинках пропуски в модельных составляющих вырезаны для наглядности).
По нашим оценкам, при заполнении пропусков нашим способом вот этот конкретный ряд СО2 восстанавливается с точностью 99.6% (в метрике дисперсии). Есть еще аналогичные данные по другим станциям, могу их тоже выложить для тестов. Мне действительно, безо всяких подковырок, интересно: а сколько получится при использовании вашего метода? Давайте попробуем, тут ведь расчетов на полчаса-час. Гораздо больше времени нужно, чтобы скачать и загрузить в свой пакет данные и "врубиться" в них.

ptr128
27.11.2022 19:29+1Вы уверены, что результат заполнения пропусков будет адекватный?
Я то уверен, так как проверял.
Ряды очень разные. Одно дело - логистика (время перевозок ж/д вагонами), а совсем дело - концентрация CO2
Для моих рядов использование ARIMA в качестве модели для фильтра Калмана дало наилучший результат из всех опробованных методов.
Прямо сейчас данные не предоставлю. Простите, им считаться часов 30-40. Но на неделе постараюсь

adeshere
27.11.2022 21:07Да, было бы интересно взглянуть. Я не прошу что-то глобальное, можно взять какую-то небольшую группу сигналов - мне просто интересно познакомиться с технологией в приложении к конкретным рядам. Понятно, что данные и задачи разные, но научиться чему-то полезному у соседа можно всегда ;-)

Tim_23
27.11.2022 15:32+1А тренд вы как вычитали? Брали некое среднее на выбранном интервале и далее "скользили" по всему ряду вычитая из данных текущее среднее?

adeshere
27.11.2022 18:18+1Нет, немного сложнее. Две основные проблемы, суперпозиция которых существенно усложняет задачу - это нестационарность и пропуски. Да, это немного смешно: та самая нестационарность, для борьбы с которой мы строим тренд, мешает его оценивать. Но если мы хотим свести все оценки к матожиданиям (чтобы раз и навсегда закрыть вопрос о пропусках данных), то проблема действительно возникает. Ну и еще в нашем случае добавляется тот нюанс, что мы строим тренд, синхронный исходному ряду, без его обрезания в начале и/или конце. А обычное скользящее среднее это сделать не позволяет.
А как именно мы все это делаем - я написал под спойлером, так как ответ получается очень длинный, и тем, кому все это не интересно, он будет мешать читать комментарии.
.
Как мы оцениваем непараметрический тренд
Как известно, для расчета обычного скользящего среднего нужно иметь данные в довольно широком окне, в котором это среднее считается. Если полученное среднее сопоставляется с серединой окна, то его принято называть симметричным, а если с его правым концом - то причинным (поскольку мы не заглядываем в будущее при оценке среднего). Но в любом варианте, если просто скользить окном сглаживания по сигналу, ряд результата будет обрезан либо в начале (если окно причинное), либо с обеих концов отрежется по половинке окна, если оно симметричное. А нам для построения модели надо, чтобы каждая составляющая сигнала была идентична ему по длине, без отрезания кусков.
Поэтому мы делаем небольшой трюк: наше скользящее окно стартует за пределами ряда (левее его начала) и останавливается немного правее конца сигнала. Подробнее эта технология описана вот в этой статье (полный текст выложил в ту же папку на Я-диске). Но если в двух словах, то и слева, и справа окно (если оно симметричное) выезжает за границу ряда на половину своего размера. При этом все значения данных вне ряда считаются пропусками (а что еще с ними делать?). То есть фактически на границах ряда (как и на границах больших серий пропусков) скользящее среднее оценивается по половине окна. И в этом не было бы никакой катастрофы, если бы ряд был стационарный, а считать нужно было только матожидание. Но на самом-то деле стационарности нет! При наличии заметного тренда (а иначе зачем его убирать?) сигнал не может считаться стационарным ни в каком приближении. (Некоторые интересные следствия из факта нестационарности реальных сигналов обсуждаются вот в этой статье на хабре). Поэтому если "в лоб" применять описанную технику скользящего окна для сигнала с трендом, то на границах интервалов пропусков возникают очевидные краевые эффекты (см. рис.1в вот в этой статье, ее полный текст выложен в той же папке).
Чтобы справиться с этой проблемой, мы оцениваем непараметрический тренд итеративно. На первом шаге из сигнала убирается параметрический тренд, заданный минимальным числом параметров (чтобы не увеличивать число степеней свободы модели). В идеале, тип этого тренда должен определяться физикой изучаемого явления, но понятно, что в реальной статистике это возможно далеко не всегда. На практике для первого приближения можно взять любую разумную функция, которая более-менее соответствует данным. В простейшем случае это может быть линейный или экспоненциальный тренд и т.д. Причем в рамках нашего подхода его не нужно подгонять идеально. Главное - чтобы удаление этого тренда позволило убрать нестационарность сигнала там, где у него 1) есть значительные серии пропусков и 2) на краях ряда. Тогда на втором шаге можно будет построить непараметрический тренд, который соберет в себя все эффекты, не учтенные "моделью первого приближения".
Для ряда СО2 мы в качестве модели первого приближения сначала взяли линейный тренд. Благо, для оценки его параметров не нужны вообще никакие трюки - обычные наименьшие квадраты рулят ;-). Но анализ остатков после вычитания этого тренда (а также сезонности) показал, что погрешность линейной модели чересчур велика (она сильно больше, чем дисперсия квазистационарной составляющей ряда). Поэтому мы чуть-чуть усложнили модель и вместо линейного тренда построили кусочно-линейный из двух кусков. Да, количество подгоняемых параметров при этом выросло до 4, зато и в начале, и в конце сигнала кусочно-линейная модель позволила почти полностью убрать нестационарность, а это, в свою очередь, позволило полноценно применить технологию "заграничного" скользящего окна для построения непараметрического тренда. Собственно, это все как раз и описано в той статье, которую я упоминал чуть выше.
Ну и последний нюанс: вместо обычного скользящего среднего мы на самом деле используем взвешенное, когда значения в середине окна имеют больший вес, чем на его краях. По-научному это называется ядерное скользящее сглаживание, хотя я не люблю использовать узкоспециализированную терминологию там, где она не особо нужна.
С формальной точки зрения, основная идея взвешенного скользящего среднего состоит в том, чтобы улучшить частотную характеристику сглаживающего фильтра. Однако тут есть важный нюанс: оптимальные (в разных смыслах) цифровые частотные фильтры обычно содержат знакопеременные последовательности весовых коэффициентов. При наличии пропусков данных такие последовательности иногда ведут себя очень плохо: в отфильтрованном сигнале возникают различные артефакты, иногда очень неприятные, и почти всегда будет сильный дополнительный шум. Потому я стараюсь использовать только весовые последовательности с положительными коэффициентами. Конкретно для СО2 мы использовали гауссово сглаживающее ядро (довольно часто это неплохой выбор). В других случаях может подойти экспоненциальное ядро, и т.п.
Ну и теперь про влияние пропусков на скользящее сглаживание. Строго говоря, при наличии пропусков мы должны отказаться от методов, ориентированных на работу с эквидистантными временными рядами, и согласиться, что моменты измерений могут быть произвольными (пусть даже и кратными какому-то найквисту). Но технически сделать это довольно проблематично. Так, весовая функция ядра в этом случае должна пересчитываться заново для каждого набора моментов пропусков данных. Но количество возможных комбинаций моментов пропусков с ростом ширины окна n растет, как 2^n. Поэтому уже при ширине окна порядка 100 точек заранее рассчитать весовые функции для всех возможных наборов пропусков (и потом просто подсовывать в сверточный оператор нужную функцию при расчетах) нереально. А у нас сплошь и рядом ширина сглаживающего окна много больше. Даже для СО2, где данные ежесуточные и сам ряд - с гулькин нос, использовалось окно в 1461 точку. А если это более высокочастотный сигнал?
Поэтому мы при ядерном сглаживании используем самодельный суррогатный подход: во время свертки вычисляется фактическая сумма весовых коэффициентов ядра, которые попали на не-пропуски (т.е. пары с пропусками игнорируются), а затем эти весовые коэффициенты перенормируются так, чтобы в сумме получить единицу. Пока пропусков относительно мало, и они распределены более-менее случайно, для положительно определенных весовых функций этот подход работает просто отлично. Чуть хуже дела обстоят на границах ряда, когда пропусков много, и все они сконцентрированы в одной половине окна. В таких случаях как раз и приходится изобретать всякие дополнительные трюки типа предварительного вычитания кусочно-линейного тренда, чтобы алгоритм работал более-менее адекватно. Но в целом численное моделирование показывает, что описанный подход вполне
имеет право на жизнь
Под численным моделированием я имею в виду подход, когда мы генерируем модельный ряд, максимально похожий на настоящий, затем его умышленно портим, добавляя шум, пропуски и т.д., а потом обрабатываем полученный зашумленный сигнал и пытаемся восстановить характеристики исходного модельного ряда. Это позволяет довольно объективно оценивать качество модели наиболее прямым способом - сравнивая результат с идеалом, который известен.
С точки зрения практической работы с геофизическими временными рядами идея декомпозиции сигнала на составляющие тоже вполне себя оправдала. Конечно, процессы в Земле и в экономике отличаются очень сильно, поэтому непонятно, насколько наши подходы применимы в другой предметной области. Но я подумал, что будет не лишним рассказать о них здесь. Надеюсь, меня простят за излишне лонгидерский комментарий...
.

Lev_Perla Автор
27.11.2022 16:25+1Задача интересная, спасибо за опыт)
Насколько я ее понял, вам требовалось не предсказать новые значения временного ряда (экстраполяция), а объяснить поведение показателя в прошлом.Модели нейронных сетей из-за своей сложной структуры достаточно тяжело интерпретировать, поэтому я бы рекомендовал попробовать библиотеку Prophet вместо них. Она по сути представляет регрессионную модель на стероидах и позволяет хорошо разложить ряд на составляющие, чтобы оценить эффект от каждого из них.

adeshere
27.11.2022 20:08На самом деле, разница между описанием и предсказанием гораздо меньше, чем кажется. После декомпозиции сигнала каждую из его составляющих можно экстраполировать в будущее достаточно тривиальными способами. На заре нашего пакета мы тоже начинали с ARIMA , однако очень быстро убедились в ее непригодности для наших задач. Одна только необходимость заполнять пропуски уже выводит ее за грань добра и зла. Ну и качество прогноза было не слишком хорошее. Но главное, применяя авторегрессионные модели, ты получаешь на выход табличку с непонятными коэффициентами, среди которых еще и отрицательные попадаются. И как их интерпретировать? Нам же ведь надо в итоге построить
объясняющую модель процесса...
Поэтому мы почти сразу пришли к выводу, что нам нужна декомпозиция на физически обусловленные составляющие. В геофизике они довольно часто присутствую в том или ином виде. Но если модель с минимальным числом параметров хорошо описывает данные, то это чаще всего означает, что ей удалось уловить какие-то внутренние закономерности сигнала. А отсюда автоматически следует и возможность дать хороший прогноз.
Например, итоговая модель атмосферного СО2 включает двухкомпонентный тренд, сезонную составляющую и относительно высокочастотный остаток. Первая компонента тренда - это кусочно-линейная функция. Она подогнана на 20-летнем интервале, то есть основная тенденция ряда за этот период меняется очень слабо. Поэтому можно принять, что экстраполяция этой составляющей на год-два и даже пять лет вперед будет иметь практически такую же ошибку, как у ретроспективных данных. А при ретроспективном анализе вся эта ошибка полностью учтена в непараметрическом тренде. Соответственно, его погрешность подгонки и нужно брать при экстраполяции.
Непараметрический тренд мы оценивали в окне 1461 сут. Понятно, что он по определению будет непредсказуем на лагах больше, чем половина окна. Если мы ходим экстраполировать непараметрический тренд на два года вперед и больше, то в качестве прогнозной оценки значения тренда надо взять ноль, а для оценки погрешности экстраполяции посчитать ретроспективно дисперсию. Вот
его график
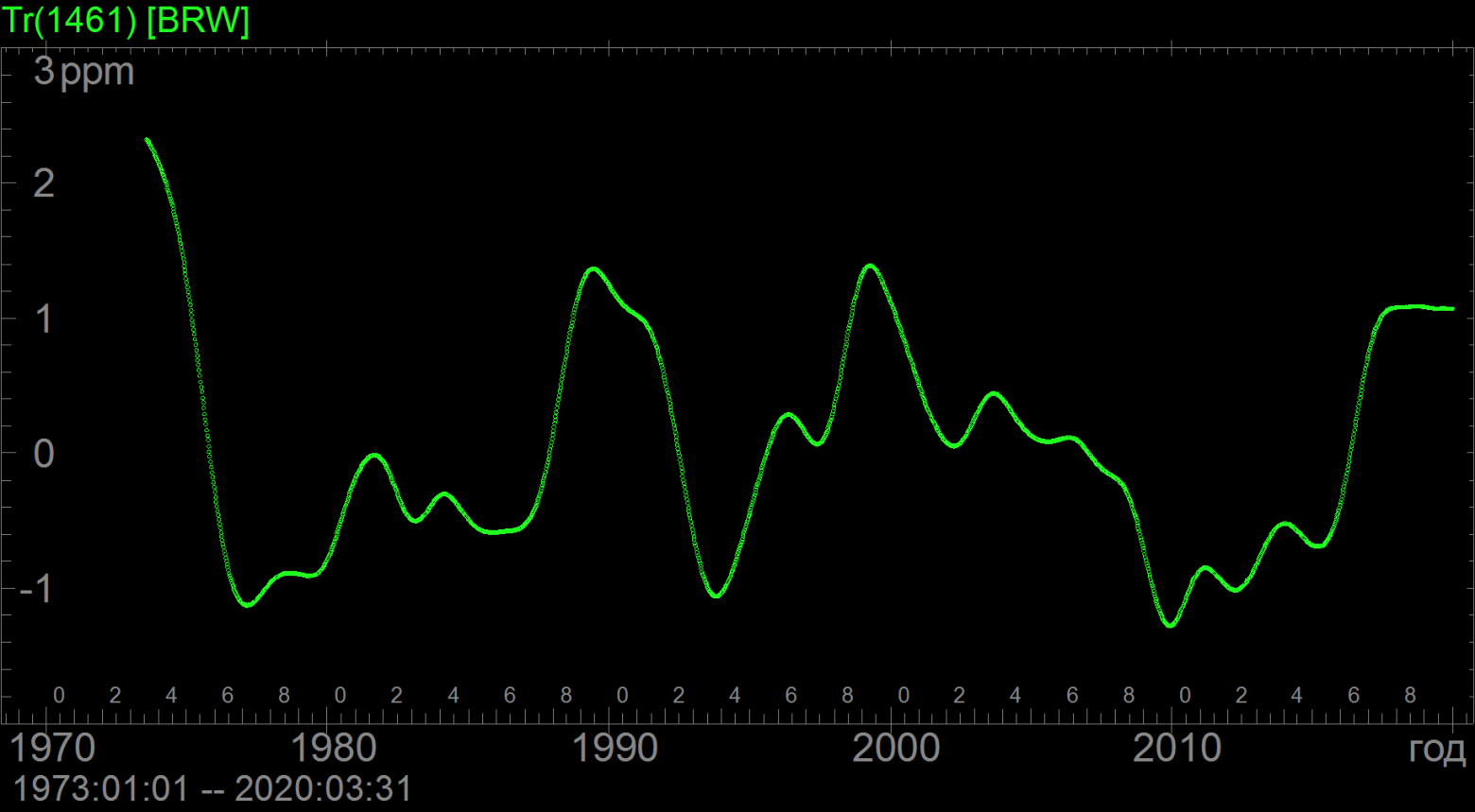
Непараметрический тренд для ряда концентрации атмосферного CO2 на ст.Барроу Расчеты показывают, что она составляет 0.1% от полной дисперсии сигнала. Следовательно, непредсказуемость непараметрического тренда дает на больших лагах ошибку прогноза 0.1%, и ее принципиально нельзя уменьшить. (Понятно что на малых лагах, т.е. порядка 100-200 точек, она будет кратно меньше; более точные цифры можно получить из коэффициентов свертки).
Теперь сезонная составляющая. Она в нашей модели представлена в виде среднесезонной функции (ССФ) с медленно растущей амплитудой. ССФ по определению строго периодическая, то есть погрешность ее экстраполяции в точности нулевая. А вот компонента, описывающая рост амплитуды сезонных эффектов - это точно такой же непараметрический тренд, только с окном 10 лет, плюс константа. Таким образом, мы можем достаточно надежно описывать сезонные эффекты на горизонте планирования не более 5 лет, а затем погрешность оценки амплитуды сезонной вариации будет равна погрешности оценивания непараметрического тренда амплитуды ССФ. Которая ретроспективно близка к 10% от константы, задающей среднюю амплитуду ССФ. Итого, при амплитуде сезонной вариации 5.65ppm получаем неопределенность долгосрочного прогноза порядка 0.5% за счет неопределенности амплитуды сезонных эффектов в будущем.
Ну и понятно, что все эти погрешности должны плюсоваться к погрешности самой модели, которая ретроспективно равна 0.4%. Итого получаем, что точность прогнозирования ряда атмосферного СО2 на небольших лагах (порядка 100 точек) будет составлять примерно 0.6%, а на больших лагах (5-10 лет, или 2-3 тыс.точек) будет порядка 1%.
Теоретически говоря, эту погрешность модно немного уменьшить, если построить дополнительную экстраполируемую модель для остаточной (высокочастотной) составляющей ряда. Для нее как раз идеально подошла бы авторегрессионная модель. Однако анализ автокорреляций показывает, что предельный горизонт экстраполяции у такой модели ничтожный (десятки-сотни точек), а выигрыш минимальный, так как вся эта компонента дает лишь десятые доли процента от полной дисперсии ряда. Соответственно, прогнозирование высокочастотных флуктуаций даст выигрыш в проценты от этих процентов. Это эффекты второго порядка малости в нашем случае.
Разумеется, эти приведенные выше оценки будут верны, только если внутренняя структура процесса не изменится кардинально. Для СО2 заметные изменения могут быть связаны, например, с приостановкой промышленных выбросов во время ковида. (Кстати, наша модель, описанная выше, построена по данным до 2019 года включительно, т.е. еще доковидным). Сейчас уже заканчивается 2022 год, поэтому реальную точность этой модели скоро вполне можно будет проверить по независимым данным (сейчас у меня пока этих данных нет). Но я думаю, что структура процессов, ответственных за изменения атмосферного СО2, вряд ли очень сильно меняется в глобальном плане даже с учетом ковида. Поэтому есть надежда, что прогноз по этой модели будет достаточно адекватным.
Другой вопрос, что в экономике тенденции развития процессов гораздо в меньшей степени определяются внутренними закономерностями, но очень сильно зависят от всяких внешних воздействий, начиная от психологии рынков и кончая волюнтаризмом отдельных влиятельных лиц. Поэтому построить объясняющие модели сравнимого качества, работающие хотя бы в масштабе десятилетий, в эконометрике вряд ли удастся. Даже если такие модели и будут работать на коротких временных интервалах, любой "черный лебедь" может все поменять до неузнаваемости. И что тогда толку от того, что ты десять лет получал на 1% больше, чем остальные, если какой-то инсайдер одномоментно может отобрать у тебя сразу все?

adeshere
27.11.2022 20:45я бы рекомендовал попробовать библиотеку Prophet вместо них. Она по сути представляет регрессионную модель на стероидах и позволяет хорошо разложить ряд на составляющие, чтобы оценить эффект от каждого из них.
Спасибо за совет! Но библиотек и пакетов есть очень много, и познакомиться со всеми не хватит никаких сил. Поэтому прежде, чем им воспользоваться, хочется убедиться, что она как минимум совместима с нашими данными и задачами. Если Вы с этой библиотекой работали, то, наверно, сможете подсказать: 1) есть ли там поддержка работы с пропущенными наблюдениями (чтобы их не требовалось искусственно заполнять перед проведением вычислений)? 2) Все ли вычисления написаны на Си или других языках с нормальной производительностью, нет ли там каких-то питоновских вставок (у нас сплошь и рядом есть ряды длиной в миллионы точек). 3) Какие форматы данных поддерживаются "из коробки", кроме csv? Например, есть ли экспорт-импорт в Zetlab-овский бинарный формат ana+anp? А то мы сотрудничаем с коллегами, которые пишут на Питоне... но обмениваться с ними данными - это боль. Попробуйте регулярно записывать и читать 100-герцовый сигнал длиной несколько лет в csv, и вы оцените наши страдания ;-) Поэтому я все-таки предпочитаю один раз загрузить эти данные в свою базу, и дальше все делать в ней ;-)
Но если ответы на три заданных выше вопроса положительные - тогда да, будет интересно попробовать интегрировать эту библиотеку в наш пакет. Благо, он построен по принципу конвейерной обработки и легко расширяется. Ведь вне зависимости от того, какая модель точнее, сравнение двух разных подходов при обработке одного ряда всегда дает очень интересную дополнительную информацию.

ptr128
27.11.2022 10:22Непонятно, почему в прогнозировании ограничились только RNN. По моему опыту, особенно при наличии сезонной составляющей, есть смысл производить кроссвалидацию с ARIMA. На некоторых временных рядах из логистики, у меня ARIMA выигрывала у RNN в половине случаев.

Lev_Perla Автор
27.11.2022 15:38+1Действительно, я в каждом эксперименте проводил сравнение с моделью ARIMA в качестве базовой. Для семидневного горизонта локальная модель RNN была в среднем точнее модели ARIMA в каждом из экспериментов.
Хочу с вами согласиться, при коротких прогнозных горизонтах ARIMA может обгонять RNN по точности. По моему мнению, в реальных проектах нужно следовать no free lunch theorem (что нет универсального алгоритма) и пробовать перебор различных моделей для получения лучшей точности для каждого ряда.

sturex
27.11.2022 15:33Попробуйте прогнозирование цены с помощью рекуррентных сетей при условии, что на входе у вас не цена, либо манипуляции с ней. Мне самому не удалось (интересы поменялись) это сделать, но на результаты я бы с удовольствием посмотрел)
Говоря "на входе не цена" я имею в виду, например, разницу между спросом и предложением в стакане к общему объему в стакане. Вам придётся пользоваться тиковыми L2 данными для этого, т.е. самому накопить реальные данные, т.к. просто цены закрытия не подойдут. (Ну или напишите мне, у меня вроде лежит пару месяцев 100 строчных стаканов)

master1985
27.11.2022 15:38Отличная статья! Сам в свое время занимался схожими исследованиями. Рассматривал ли вариант объединения нескольких алгоритмов в ансамбли? Если нет, то почему?

Lev_Perla Автор
27.11.2022 15:44Моя исследовательская работа была направлена на изучение конкретно RNN моделей их поведения в разных условиях, поэтому ансамбли я в ней не захватил (если не считать вариаций direct стратегии, которые по сути и есть ансамбли).
В моих рабочих проектах я использовал ансамбли прогнозных моделей и это даже помогало увеличить точность прогнозной системы. Но к экспериментам с ними стоит переходить только после того, как построил систему с перебором отдельных моделей.

fortser
28.11.2022 10:08гораздо выгоднее прогнозировать не абсолютное изменение цены , а относительное. можно брать единицы волатильности, можно просто процент изменения . создаем например 5 классов : [ значительное падение , незначительное падение , около нулевые колебания , незначительный рост , значительный рост ]. далее можно варьировать соотношение обучающей выборки , от равномерного до нормального распределения в каждом классе . и да , поскольку финансовые рынки склонны к трендам, обязательно нужно включать фактор авторегрессии с лагом на смежных рынках

vladimircape
28.11.2022 11:55тут вопрос не в "выгодности", а в том что ,если модель видела только абсолютные изменения цены,например от 5 до 7, то после тренировки если она получит значения что не видела например 8, она начнёт безбожно ошибаться. Также лучше нормализацию делать для всех нейронных сетей, чтобы модель легче сходилась

vladimircape
28.11.2022 11:09Этой статье как раз и место в песочнице. Уже давно никто в современных решениях не применяет рекуррентные сети для временных рядов. Временные ряды проходят лишь в качестве общего понимания что такие есть. Существует много решений что их обходят по качеству . Хотя-бы посмотрели бы wavenet или потоки для начала. Не учите людей не нужному. Также метод скользящего окна ваш не верен. Надо хотя-бы делать gap между тренировочными и текстовыми, т.к вы data leaks допустили, особенно в финансовой сфере . Также согласно вашей статьи видно вы не понимаете зачем делается логарифмирование и как его правильно делать. Вам не стабилизацию дисперсии надо делать , а проверять ряд на стационарность и одного логгарифмирования бывает недостаточно, поэтому после каждого преобразования ещё раз проверяют на стационарность, а не дисперсию. Прямо читаю вашу статью и вижу всю академичность нашу российскую которая плоха. Вы берете метрики mape но это метрика не показатель , есть случаи что она не отражает качество модели. Считаю что это не тянет на магисторскую работу.

Lev_Perla Автор
28.11.2022 11:17Спасибо за критику!
Конечно соглашусь с вами, что существуют модели, превосходящие RNN по качеству. Более того склоняюсь к тому, что не существует универсальной модели, которая бы подходила для всех временных рядов.
Насчет того, что модели RNN никто не использует давно, не соглашусь. После победы модели ES-RNN на M4 число статей в иностранных журналах, посвященных использованию RNN для прогнозирования, кратно увеличилось в 2020-2021 годах. Среди статей по финансовому прогнозированию модели RNN тоже лидировали в эти года. Правда в этом году начали выходить статьи по результатам соревнования M5, на котором уже первенство забрали LightGBM, возможно, сейчас интерес перейдет к ним)
Также метод скользящего окна ваш не верен. Надо хотя-бы делать gap между тренировочными и текстовыми, т.к вы data leaks допустили, особенно в финансовой сфере
Скользящее окно используется только для разбиения тренировочной выборки на части, которые RNN модель лучше усвоит, тестовая откладывается до этого шага обработки, поэтому data leak не происходит.
Вам не стабилизацию дисперсии надо делать , а проверять ряд на стационарность
Для моделей машинного обучения и нейронных сетей нет жестких требований к стационарности временных рядов, как в случае эконометрических моделей, поэтому на это акцент я не делал.

vladimircape
28.11.2022 11:53Не тратье время на временные ряды время, это ушедшая архитектура сетей. Поиграйтесь еще со statefull , т.к поведение сети разное.
Насчёт универсальной модели, ну могу сказать что авторегрессионные модели типа AR и производные типа SARIMAX,Facebook Prophet это прошлый век, и они проигрывают даже xgboost. Поэтому деревья решения более универсальны, плюс еще хорошо ложатся на всякие системы интерпретации типа shap.
Насчет М4. Если я правильно помню, там были данные с сезонностями и прочие искусственности, в реальности такое редко встретишь,и они сделали 4года назад(для направления машинного обучения это уже считается давно, быстро меняются алгоритмы) и сделали это как универсальный аппроксиматор, т.е попытались подогнать под все решения, что в жизни плохо работает, вот вы проверяли, смогло ли это решения, побить самое "тупое" dummy решение, мол будущее целевое значение равно текущему.
Насчет data leak вы так и не поняли. По простому ,например если у вас интервал 1 минута, надо как минимум ставить gap 60минут, (все индивидуально), ибо значения тренировки могут быть инертны и залезть в будущее. Поищите обязательно это уже давно стандарт.
Насчёт стационарности вы глубоко ошибаетесь. К примеру я занимался прогнозированием в трейдинге, где ряды ну никак не стационарны, и люди всё равно стараются сделать хоть как-то стационарными, ибо ваша модель будет не работоспособная, даже иногда может и не сойтись. Для простоты понимания ,вот вам пример. за 2022 год(вы на нем тренировали), у вас акция колебалась в ценовом диапазоне, от 10 до 13 рублей, т.е +/-30%, наступил 2023 и акция или с 10 упала до 2 , или с 13 до 30, т.е может и -80% или +130%, Если вы тренировали на сырых данных т.е целевое было от 10 до 13, то отдельные модели не зная чисел меньше 10 и больше 13, просто начнут выдавать бред. Если же вы даже слогарифмируете,то не поможет, даже если вы перейдете к процентному изменения цены, то модель все равно не видела большие изменения, поэтому как минимум используют log(diff) логарифм изменения.
очень часто мне приходилось от заказчиков переделывать решения т.к они не работали ,по предсказаниями временных рядов, там тоже академики любят авторегрессии, строят красивые объяснения, а по факту не работает.

serebryakovsergey
28.11.2022 17:18Насчет data leak вы так и не поняли. По простому ,например если у вас интервал 1 минута, надо как минимум ставить gap 60минут, (все индивидуально), ибо значения тренировки могут быть инертны и залезть в будущее. Поищите обязательно это уже давно стандарт.
Порекомендуйте, пожалуйста, статью на эту тему.

vladimircape
28.11.2022 21:17К примеру если вы используете лаги, то в тестовом наборе вначале будут данные из обучающей выборки, если нет пробелов.
Всё не помню,но вот про что я говорю
https://towardsdatascience.com/proper-validation-of-a-time-series-model-5c1b54f43e60
https://tscv.readthedocs.io/en/latest/tutorial/leave_p_out.html
http://rasbt.github.io/mlxtend/user_guide/evaluate/GroupTimeSeriesSplit/
https://docs.h2o.ai/driverless-ai/latest-stable/docs/userguide/time-series.html




flass
Здравствуйте! Спасибо за статью. Задача прогнозирования временных рядов, как вижу, успешно решена. Применим ли данный метод к прогнозированию биржевых курсов валют?
Lev_Perla Автор
Доброго дня! Да, этот метод также можно применять для прогнозирования биржевых курсов. В этой статье упоминаются некоторые из таких исследований.
Однако стоит учитывать, что многие специалисты скептически относятся к прогнозированию любых биржевых показателей, так как часто их динамика зависит от текущих настроений и мнений инвесторов на рынке, а не от исторических паттернов.
Пытаясь решить эту проблему, исследователи с помощью рекуррентных нейронных сетей включают в прогнозные модели анализ новостей (NLP задача). Сейчас как раз проходит международное соревнование M6, которое направлено на прогнозирование финансовых временных рядов и биржевых показателей. Будем ждать по его результатам новых открытий и методов)