Алгоритмы являются фундаментальными строительными блоками в программировании и играют важнейшую роль в современном мире, основанном на технологиях. Они представляют собой набор инструкций для эффективного выполнения задач, таких как сортировка данных, поиск в базах данных и составление прогнозов. Автоматизируя эти процессы, алгоритмы помогают экономить время, сокращать количество ошибок и принимать обоснованные решения. Они лежат в основе многих технологий, которые мы используем в повседневной жизни, от социальных сетей до электронной коммерции, и оказывают значительное влияние на различные отрасли, от финансов до здравоохранения.

Например, практически каждый современный графический редактор предоставляет своим пользователям множество полезных и удобных инструментов. Один из таких инструментов — функция заливки однородной области указанным цветом. 

Работает она очень просто: необходимо выбрать желаемый цвет заливки и кликнуть указателем мыши на нужную область изображения. В результате выбранный регион изменит цвет на указанный. Этот механизм реализуется специальным алгоритмом, который носит название «метод „наводнение“», или, по-английски, flood fill. 

В этой статье мы возьмём интересную задачу с собеседования, которую можно решить при помощи алгоритма flood fill, разберём её и познакомимся с несколькими вариантами решения. В этом поможет Евгений Бартенев, техлид и автор курса «Python-разработчик» в Яндекс Практикуме.

Постановка задачи

Графические редакторы — это не единственное место применения данного алгоритма. Схожие механизмы можно встретить и в других сферах, например:

• Разработка игр. Заливка часто используется в разработке игр для реализации таких функций, как рисование, генерация рельефа и создание лабиринтов.

• Компьютерная графика. Алгоритм заливки используется в компьютерной графике для таких задач, как заливка фигур цветом, обнаружение связанных областей и генерация текстур.

• Компьютерное зрение. Заливка используется в компьютерном зрении для решения таких задач, как распознавание объектов, сегментация изображений и определение границ областей.

• Генерация карт. Заливка может использоваться для создания карт путём заполнения регионов различными типами рельефа.

В целом алгоритм заливки является универсальным и широко используемым методом, который полезен во многих задачах.

Более того, задачи, которые можно решить, используя этот алгоритм, довольно часто встречаются на собеседованиях в различные ИТ-компании. Его возможные реализации базируются на фундаментальных знаниях, которыми должен обладать каждый современный разработчик. 

Задача

В примере работы с графическим редактором речь шла о заливке выбранной однородной области изображения заранее указанным цветом. Но что такое изображение глазами разработчика? И что такое однородная область? 

Изображение — это просто матрица, двумерный массив пикселей, каждый из которых содержит в себе информацию о цвете, а если точнее — о коде цвета. 

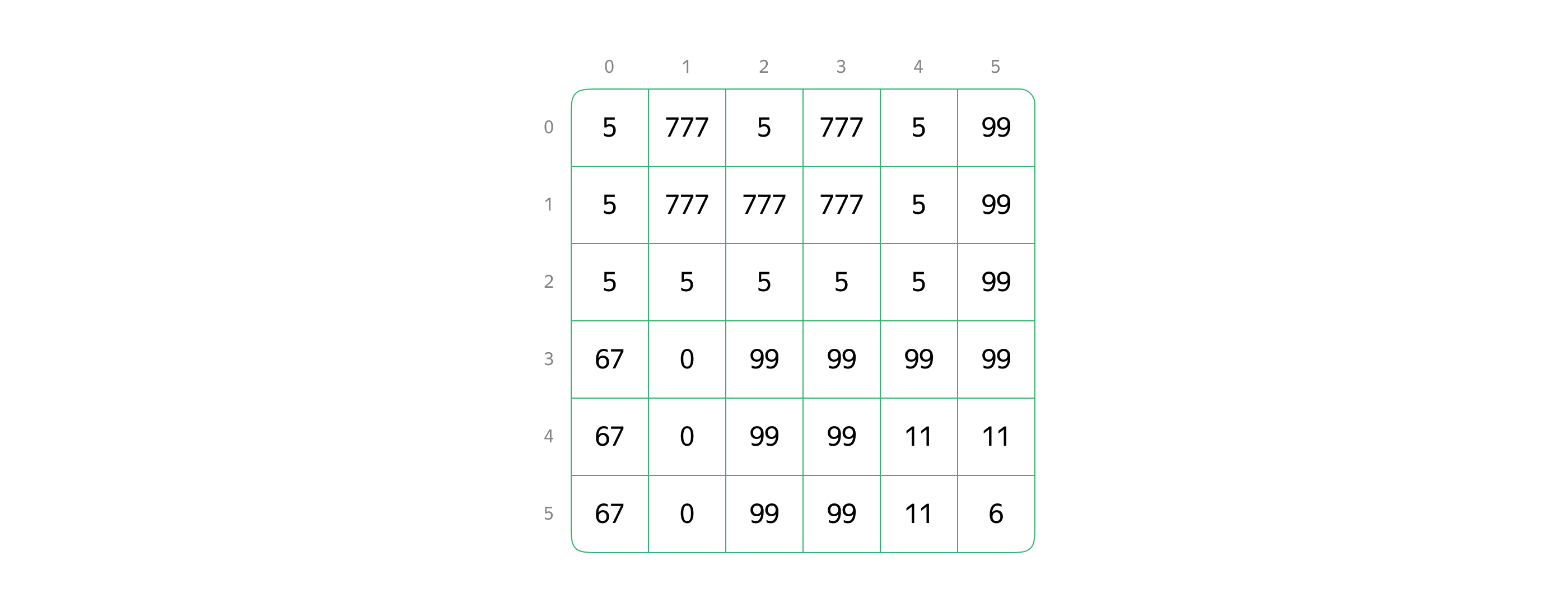
Значит, можно сказать, что однородная область — это совокупность соседствующих ячеек матрицы, содержащих одинаковые значения.

Когда пользователь нажимает на какую-либо область изображения для её заливки, то фактически он указывает на одну из ячеек матрицы. Таким образом, задачу можно сформулировать следующим образом:

Дана матрица размером x строк и y столбцов. Каждая ячейка содержит целочисленное значение. Положим, что возможные значения для каждой ячейки лежат в диапазоне от 0 и до 1000 включительно. 

Ваша задача — написать функцию FloodFill, которая принимает четыре параметра:

• matrix — исходная матрица,

• x и y — координаты стартовой ячейки,

• newValue — новое значение.

Задача функции — изменить значения для всей совокупности соседствующих ячеек на новые, если их значение идентично значению указанной ячейки.

Например, в результате вызова функции FloodFill с параметрами (matrix, 3, 3, 66) матрица примет следующий вид:

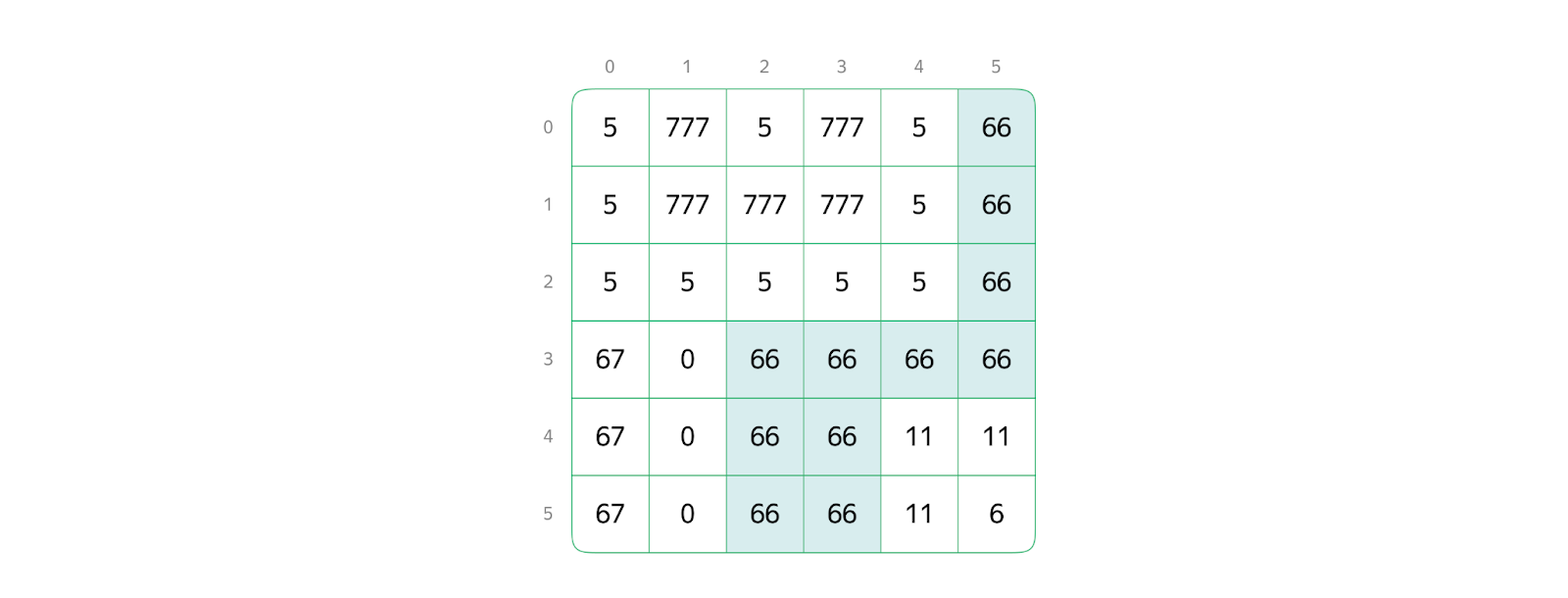
Ячейка с координатами (3, 3) с изначальным значением 99, как и все её соседи с таким же значением, получила новое значение — 66.

Задача сформулирована, но как её решить?

Поиск решения

Быстрое решение, которое может первым прийти в голову, заключается в том, чтобы пробежаться по всем элементам матрицы и поменять значение у тех ячеек, в которых значение будет равно значению ячейки, указанной при вызове функции.

Такой простой подход позволит быстро выполнить задачу и закрасить выбранную однородную область. Однако если в матрице найдутся и другие однородные области с таким же изначальным значением, то будут закрашены и они. А этого нас никто делать не просил.

Такое быстрое решение тут не подойдёт.

Лабиринт

На используемую в задаче матрицу можно посмотреть и по-другому — например, как на лабиринт. 

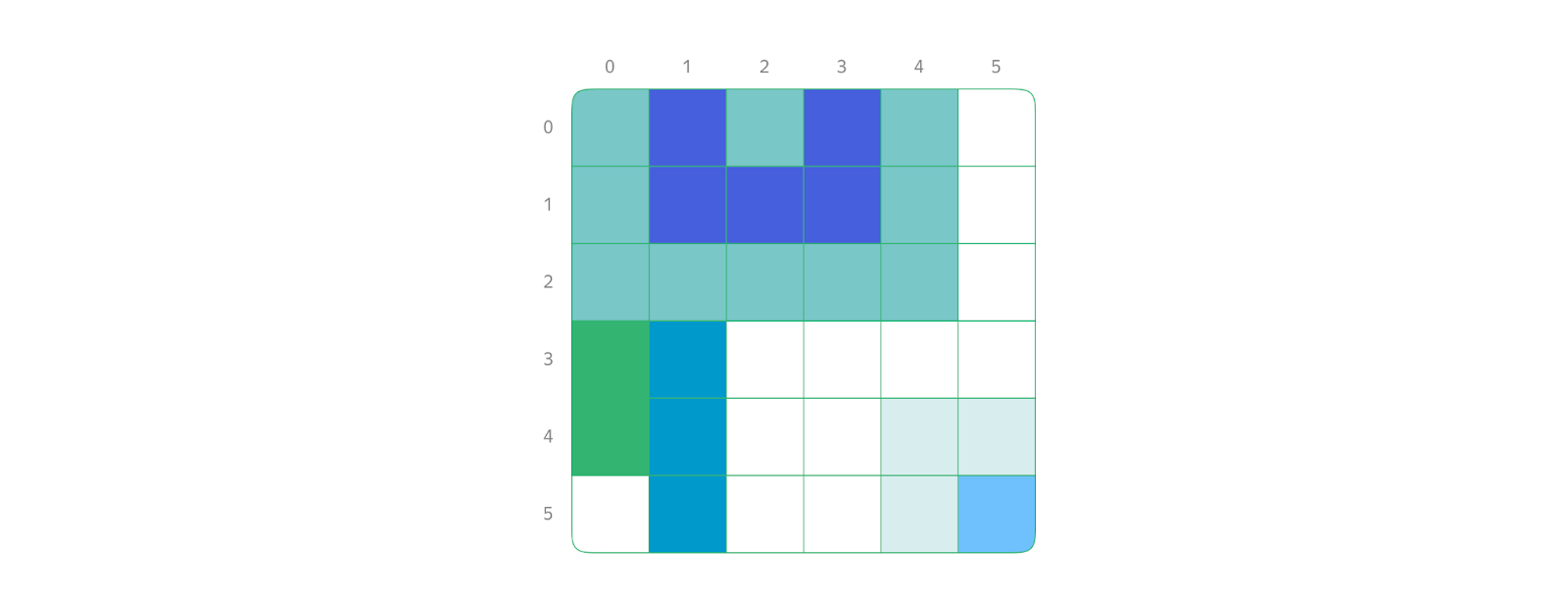
Оказавшись в определённой стартовой точке или ячейке этого лабиринта, можно принять следующие правила:

• ячейки с таким же значением — проходимые;

• ячейки с любыми другими значениями — непроходимые, или просто стены.

Тогда задача сводится к тому, чтобы исследовать этот загадочный лабиринт относительно стартовой ячейки, посетив все проходимые ячейки в пределах стен и поменяв их значения на новые.

Всего возможно четыре направления движения по лабиринту: влево, вправо, вверх и вниз. Тогда в общем виде алгоритм выполнения поставленной задачи будет выглядеть следующим образом: 

1. Перейти в какую-либо проходимую соседнюю ячейку и обновить её значение.

2. Обойти все проходимые соседние ячейки из этой ячейки, обновляя их значения.

3. Вернуться в начальную ячейку.

4. Повторить алгоритм для всех остальных проходимых ячеек, смежных с изначальной.

Уже сейчас понятно, что алгоритм рекурсивный: для обхода всей доступной области нужно перемещаться в доступные проходимые ячейки и повторять одни и те же действия. 

Тут возникает проблема зацикливания: если из ячейки А можно перейти в ячейку Б, то из ячейки Б можно перейти в ячейку А — и рекурсия будет бесконечной. Решить эту проблему можно, применив очень простую идею: нам не нужно идти в ту ячейку, в которой мы уже были ранее. 

Тогда уточнённый порядок действий будет таким:

1. Выбрать направление движения из стартовой ячейки и выполнять движение в этом направлении до попадания в тупик.

2. После попадания в тупик нужно вернуться назад вдоль пройденного пути, пока не будет обнаружена смежная проходимая ячейка, в которой мы ещё не были, и двигаться в этом направлении.

3. Исследование лабиринта будет завершено при возвращении в стартовую ячейку.

matrix = [
   [5, 777, 5, 777, 5, 99],
   [5, 777, 777, 777, 5, 99],
   [5, 5, 5, 5, 5, 99],
   [67, 0, 99, 99, 99, 99],
   [67, 0, 99, 99, 11, 11],
   [99, 0, 99, 99, 11, 6]
]


def flood_fill(matrix, x, y, new_value):
   x_len, y_len = len(matrix), len(matrix[0])
   color = matrix[x][y]
   if color == new_value:
       return matrix


   def fill(r, c):
       if matrix[r][c] == color:
           matrix[r][c] = new_value
           if r >= 1: fill(r - 1, c)
           if r + 1 < x_len: fill(r + 1, c)
           if c >= 1: fill(r, c-1)
           if c + 1 < y_len: fill(r, c + 1)


   fill(x, y)
   return matrix


print('Изначальная матрица:')
print('\n'.join('\t'.join(map(str, row)) for row in matrix))


flood_fill(matrix, 3, 3, 66)


print('Обновлённая матрица:')
print('\n'.join('\t'.join(map(str, row)) for row in matrix))

Запустите код и проверьте результат — в однородной области вокруг указанной ячейки должны поменяться значения.

С точки зрения оценки временной сложности производительность алгоритма зависит от количества пикселей в изображении и размера заполняемой области. Алгоритм выполняет один рекурсивный вызов для каждого пикселя в регионе, и в худшем случае все пиксели в регионе будут посещены. Поэтому временная сложность алгоритма заливки на основе рекурсии может быть выражена как O(m * n), где m и n — количество строк и столбцов в изображении.

Что касается пространственной сложности, то каждый рекурсивный вызов требует дополнительной памяти для хранения состояния функции, которое включает текущую позицию и цвет пикселя.

Неожиданное откровение

Решение получилось достаточно лаконичным, однако оно не всегда будет эффективным, особенно когда речь идёт о рекурсии.

Рекурсия — это способ организации обработки данных, при котором функция вызывает саму себя. Каждый вызов функции требует выделения памяти в стеке, например для аргументов и локальных переменных. 

При большом количестве таких вызовов можно израсходовать всю память, выделенную под стек вызовов, или, иными словами, переполнить его, что обычно приводит к аварийному завершению работы. А иногда глубина рекурсии и вовсе может быть жёстко ограничена, и её может не хватить для решения задачи, например, при огромном количестве ячеек.

У изображения может быть большое разрешение, а это значит, что и сама матрица будет очень большой, то есть мы можем столкнуться с ограничениями рекурсии. 

Рекурсивный процесс в общем, упрощённом виде можно представить как работника, который все дела откладывает на пятницу. В течение недели у него мало работы, а в пятницу завал. Но пятницы может и не хватить, чтобы всё доделать.

Возможно, этому работнику стоит делать все дела при первой возможности. Тогда его работа будет равномерно распределена по неделе, а пятница будет просто обычным рабочим днём. Именно так работает итеративный подход. Любой алгоритм, реализованный в рекурсивной форме, может быть переписан в итерационном виде, и наоборот. Для итеративного решения задачи можно воспользоваться такими структурами данных, как очередь или стек.

Попробуем решить эту же задачу по-другому — итеративно. 

Уберём рекурсию из решения и заменим её на использование стека. В этом случае, как только ячейка просмотрена, она помещается в стек. При этом она будет считаться использованной, когда рядом с ней больше нет проходимых ячеек. Опишем это в коде.

matrix = [
   [5, 777, 5, 777, 5, 99],
   [5, 777, 777, 777, 5, 99],
   [5, 5, 5, 5, 5, 99],
   [67, 0, 99, 99, 99, 99],
   [67, 0, 99, 99, 11, 11],
   [99, 0, 99, 99, 11, 6]
]


def flood_fill(matrix, x, y, new_value):
   x_len, y_len = len(matrix), len(matrix[0])
   color = matrix[x][y]
   if color == new_value:
       return matrix
   stack = [(x, y)]
   while stack:
       r, c = stack.pop()
       if matrix[r][c] == color:
           matrix[r][c] = new_value   
           if r + 1 < x_len:
               stack.append((r + 1, c))
           if r - 1 >= 0:
               stack.append((r - 1, c))
           if c + 1 < y_len:
               stack.append((r, c + 1))
           if c - 1 >= 0:
               stack.append((r, c - 1))
   return matrix


print('Изначальная матрица:')
print('\n'.join('\t'.join(map(str, row)) for row in matrix))


flood_fill(matrix, 3, 3, 66)


print('Обновлённая матрица:')
print('\n'.join('\t'.join(map(str, row)) for row in matrix))

Запустите программу на выполнение и удостоверьтесь, что код выполняет поставленную задачу.

Одним из отличий решения является то, что теперь мы используем собственный механизм работы со стеком, а не тот, что используется для рекурсивных функций. Это означает, что при необходимости мы можем контролировать размер стека и правильно останавливать алгоритм вместо того, чтобы просто позволить программе аварийно завершить работу. 

Что касается временной сложности, то и рекурсивная, и итеративная реализации имеют одинаковую сложность O(m * n), где m и n — количество строк и столбцов в изображении соответственно. Это объясняется тем, что оба алгоритма посещают каждую ячейку в области не более одного раза.

Метод правой руки

Существует известный способ нахождения выхода из лабиринта, который носит название «метод правой руки». Суть его очень проста — вы кладёте правую руку на стену лабиринта и поддерживаете постоянный контакт, пока идёте по нему (конечно, вы можете использовать и левую руку вместо правой). Если все стены смежные, то метод правой руки гарантирует, что вы либо достигнете выхода, либо вернётесь к входу.

Но этот принцип можно использовать не только для поиска выхода из лабиринта, но и для решения нашей задачи. Причём решение, в основе которого лежит правило правой руки, позволяет достичь результата в условиях небольшого, ограниченного объёма памяти. А этого не позволяют сделать уже рассмотренные варианты решения.

Попробуйте самостоятельно придумать и реализовать алгоритм решения задачи методом правой руки. А если хотите написать решение, но пока не знаете как, то научиться решать подобные задачи вам поможет курс Яндекс Практикума «Алгоритмы и структуры данных».