На данный момент геометрическое ядро C3D стремительно набирает популярность вместе с КОМПАС-3D — система автоматизированного проектирования (САПР). Чтобы поддержать эту тенденцию, мы наращиваем функционал наших продуктов и вводим больше новых «фич» (features). Одним из таких нововведений является операция продления пространственной кривой на заданную длину в метрическом пространстве.
Иными словами, есть кривая длины L. Нужно построить кривую длиной L+Δl (Δl — входной параметр) такую, чтобы исходная кривая была включена в новую, а дополнительный участок размещался либо перед началом исходной кривой (в таком случае мы далее будем говорить, что кривая продлевается «в начале»), либо после ее конца (кривая продлевается «в конце»).
Описание операции продления кривой
Возможные способы продления
Первое, что хочу отметить, — это то, что пользовательский API для нового функционала предусматривает работу только с пространственными (3D) кривыми. Но в C3D к таким кривым относится и кривая на плоскости. Поэтому внутренняя реализация алгоритма затрагивает и плоские (2D) кривые. По понятным причинам эти (2D и 3D) кривые не должны быть замкнутыми. После продления 2D‑кривых результат помещается на ту же самую плоскость, на которой была исходная кривая.
Следует учесть, что 2D‑кривые являются еще и частью кривых на поверхности. В этом случае существует возможность продления поверхностной кривой через соответствующую двумерную. Об этом будет сказано ниже.
В зависимости от требуемого значения гладкости результирующей (продленной) кривой мы ввели три возможных способа продления:
1. Продление «по касательной» или «линейный» способ. Задача сводится к восстановлению касательной в заданной точке кривой и откладыванию вдоль нее отрезка заданной длины. При таком способе продления мы обеспечиваем гладкость G1на выбранном конце исходной кривой.
2. Продление «по дуге» или «круговой» способ. Математически его было бы правильно назвать «по соприкасающейся окружности». Строится окружность, радиус которой равен радиусу кривизны исходной кривой в точке продления. Плоскость этой окружности задается плоскостью векторов
трехгранника Френе (система ортонормированных векторов касательной t, нормали n и бинормали b к кривой) и проходит через точку продления. При таком способе продления мы обеспечиваем гладкость не ниже C2.
3. Продление «той же кривой» или «натуральный» способ. Если говорить о нем в двух словах, то (с учетом того, что в C3D используется параметрический способ задания кривых и поверхностей) можно сказать так: «Сохранить уравнение исходной кривой, изменив только диапазон задания параметра».
Результаты применения каждого из перечисленных способов продления (с обоих концов) для плоской кривой приведены на Рис. 1.
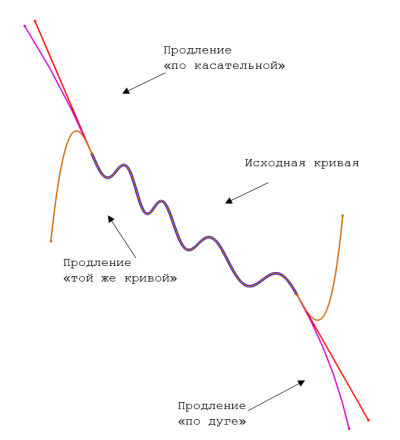
«той же кривой» (коричневый). Исходная кривая синяя
Первые два способа являются хорошо известными (и даже хрестоматийными — из классических учебников) задачами, поэтому для данной статьи большого интереса не представляют. В дальнейшем мы будем говорить только о натуральном способе продления.
Заметим, что при продлении NURBS-кривых (об этом будет сказано ниже) мы не расширяем диапазон задания параметра (точнее, репараметризуем результат таким образом, чтобы обеспечить ту же область определения, что и у исходной кривой).
Вторая особенность натурального способа продления связана с тем, что мы не всегда в качестве продленной кривой возвращаем кривую того же типа, что и исходная (т. е. название способа «той же кривой» в данном случае не совсем верное). Возможны случаи, когда кривую трудно описать с помощью уравнения или само уравнение имеет ограниченную область определения параметра. В этом случае продлевается не сама кривая, а к ней пристраивается NURBS-сегмент таким образом, чтобы в месте стыка обеспечивалась гладкость не хуже C3 (на Рис. 1 кривая продлена именно таким образом). В качестве результата возвращается составная кривая (контур). Далее для краткости мы такой способ продления (контуром с NURBS-сегментом) будем называть «общим типом».
Продление кривой, основанной на другой кривой
К типовым примерам подобных кривых можно отнести эквидистанту. Она представляет собой кривую, каждая точка которой является смещением (параллельным переносом) соответствующей точки некоторой базовой кривой на определенный вектор. Сам вектор при этом может быть константным (по величине и направлению) или являться функцией от параметра базовой кривой. Пример эквидистанты показан на Рис.2.

Здесь существуют две возможности продления. Назовем их способами «Общий натуральный» и «Базовый натуральный». Различия в поведении каждого из них будут проявляться только для указанных типов кривых (которые основаны на других кривых). Для всех остальных типов кривых результат продления при выборе базового или общего способа будет абсолютно одинаковым.
Общий натуральный способ продления как раз и был описан ранее. Единственное, что можно добавить: если кривая основана на другой кривой, она всегда будет продлеваться по общему типу. Только NURBS‑сегмент в этом случае будет пристыковываться не к базовой кривой, а к самой продлеваемой.
Суть Базового алгоритма состоит в том, что продление исходной кривой осуществляется через продление базовой. В дальнейшем к продленной базовой кривой будет применяться тот же принцип, что и к исходной кривой. Этот алгоритм на самом деле таит в себе множество нюансов и поэтому пока не доступен для полноценного использования в промышленном продукте (C3D).
Следует также отметить, что усеченная кривая (представляющая собой некоторый участок базовой кривой) продлевается всегда(!) через базовую кривую. Первоначально она продлевается до границ исходной кривой, если при этом требуемая длина не достигнута, то осуществляется продление уже базовой кривой в зависимости от ее типа.
Другие опции продления
Из всего сказанного выше следует, что алгоритм имеет два основных входных параметра: способ продления и длина продления. Укажем еще опции – входные параметры алгоритма.
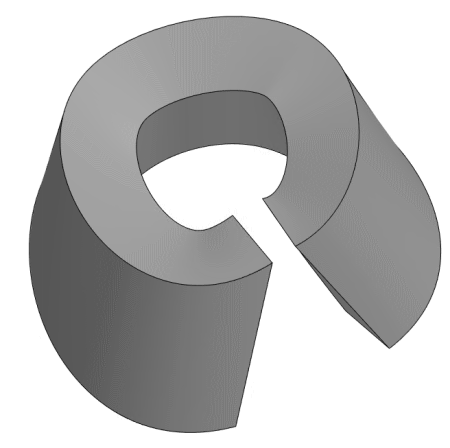
1. Флаг разрешения замкнутости. В процессе продления кривая может замыкаться, но на практике получение именно замкнутых кривых не всегда желательно. Например, при построении обечаек (см. Рис. 3). Если данный флаг установлен в false, кривая в процессе продления никогда не замкнется, т. е. всегда останется некий зазор между ее концами. Если же данный флаг установлен в true, то кривая будет продлеваться до тех пор, пока не станет замкнутой. Если же кривая в принципе не замыкается при продлении, то снятие/установка этого флага для нее не будет играть абсолютно никакой роли.
2. Флаг продления вдоль поверхности. Кривая на поверхности может быть продлена по общему типу или посредством продления соответствующей двумерной кривой и помещением результата на ту же поверхность, на которой лежит исходная кривая. Второй путь для краткости будем называть Продлением вдоль поверхности.
Различие между такими подходами можно проследить на Рис. 4. Там приведена поверхность вращения с произвольной поверхностной кривой на ней (голубым цветом) и выполнено продление по дуге в обоих случаях. Если продлевать как пространственную кривую, удлиненный участок (фиолетовый) будет именно дугой окружности, но при этом может покинуть поверхность. При продлении же вдоль поверхности кривая всегда остается на поверхности, но сам продлевающий сегмент (оранжевый) может принимать довольно интересную форму.
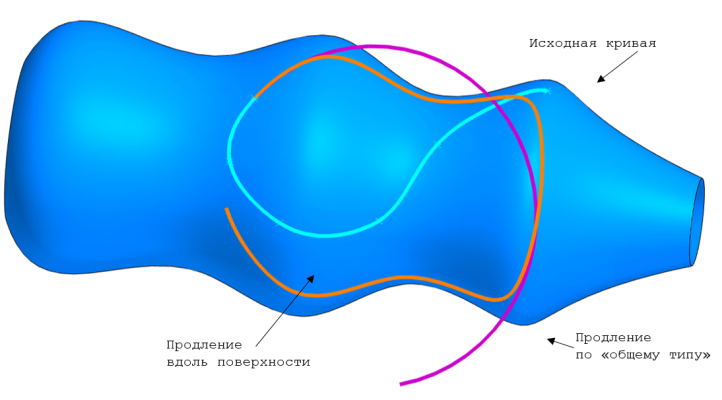
общим типом (фиолетовая). Исходная кривая голубая
Алгоритм продления NURBS-кривой натуральным способом
Приведем в качестве примера алгоритм продления NURBS-кривых натуральным способом. Для начала остановимся на продлении нерационального NURBS, потом посмотрим, как можно минимальными усилиями изменить алгоритм таким образом, чтобы обеспечить продление рационального NURBS.
Мы надеемся, что читатель немного знаком с теорией сплайновых кривых и, в частности, с NURBS, но, в любом случае, расширить свои познания он может с помощью книг [1] и [2].
Один из способов реализации описанных ниже алгоритмов заключается в том, чтобы явно вывести все необходимые зависимости для сплайнов, например, четвертого порядка. В этом случае, если придет сплайн иного вида, можно применить к нему известные алгоритмы повышения/понижения степени и все равно получить сплайн четвертого порядка. А в дальнейшем после выполнения продления, с помощью тех же алгоритмов, преобразовать результат в сплайн того же порядка, что и у исходного. Однако мы пошли другим путем. А именно…
Продление нерациональных NURBS
Напомним, что нерациональный NURBS порядка p представляет собой кусочно-заданную кривую, каждая компонента радиус-вектора которой является полиномом степени p - 1. В общем виде радиус-вектор точки кривой, соответствующей параметру τ, можно записать следующим образом:
где {Pi} – вектор контрольных точек. Границы каждого «куска» (интервал или span в иностранной литературе) определяются узловым вектором {ti}. Он задает базисы NURBS следующим образом:
При продлении NURBS‑кривой соответствующий ее интервал продлевается той же полиномиальной зависимостью, которая выполняется на продлеваемом конце. Основная трудность — получить эту зависимость для произвольно выбранного NURBS. В C3D эта задача решается с помощью разложения в ряд Тейлора в окрестности продлеваемого конца. Поскольку зависимость полиномиальная, мы обходимся конечным количеством членов ряда и восстанавливаем именно точную зависимость, а не аппроксимационную.
После того как аналитическое уравнение продлеваемого конца получено, необходимо сделать отступ вдоль кривой на заданную метрическую длину Δl > 0. Для этого, решая уравнение (3) численными методами, необходимо найти недостающий предел интегрирования: t0' в случае продления в начале (при условии, что t0 — нижняя граница области задания кривой) или t0 в случае продления в конце (при условии, что t0' — верхняя граница области задания кривой).
После того, как найден конечный параметр продленной кривой, можно переконфигурировать узловой вектор результирующего NURBS и пересчитать его базисные функции (напомним, что базисные функции определяются только узловым вектором NURBS). Зная их, можно пересчитать контрольные точки таким образом, чтобы кусок продленного сплайна на соответствующем участке совпадал с куском исходного.
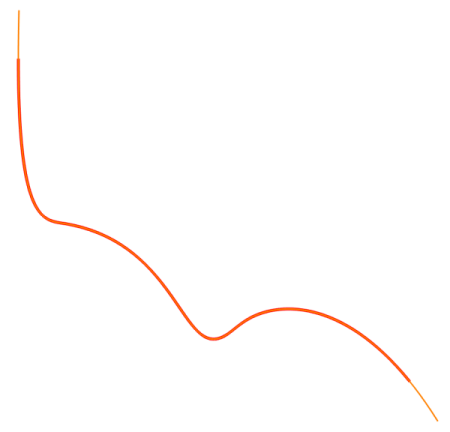
Теперь задачу продления можно считать решенной: для продленного нерационального NURBS посчитаны узловой вектор и вектор контрольных точек. Этого достаточно для задания самого сплайна. В заключение на Рис. 5 изобразим пример исходного и продленного NURBS (продление выполнено и в начале, и в конце).
Продление рациональных NURBS
Главное отличие рациональных NURBS от нерациональных в том, что в рациональном каждой контрольной точке Pi поставлен в соответствие ее вес wi > 0, при этом радиус-вектор каждой точки кривой вычисляется по формуле:
В случае, когда все контрольные точки имеют равные веса (равны 1), мы получаем описанный выше нерациональный NURBS. В случае рационального сплайна мы также имеем кусочную зависимость и также должны ее восстановить на соответствующем конце продлеваемой кривой. Специфика здесь в том, что данная зависимость уже не полиномиальная, а выражается дробно‑рациональной функцией (числитель и знаменатель — полиномы). По этой причине уже не получится обойтись конечным количеством членов ряда Тейлора.
Можно свести задачу к ранее решенной (для нерационального NURBS) путем нахождения зависимости не для всей кривой, а отдельно для числителя и отдельно для знаменателя. В случае необходимости вычисления производных от уравнения кривой (как, например, в формуле (3)), это можно сделать, вычислив производные отдельно числителя и отдельно знаменателя.
После переконфигурирования узлового интервала и пересчета базисных функций нам нужно добиться совпадения полиномиальной зависимости знаменателей исходного и продленного NURBS (они имеют полиномиальный характер, поэтому поступаем так же, как и в случае с нерациональным сплайном). Таким образом, можно найти вектор весов продленного сплайна. Подставив найденные веса в числитель продленного NURBS и потребовав его совпадения с числителем исходного, можем найти недостающий вектор контрольных точек.
Таким образом, для результирующего (продленного) рационального NURBS мы нашли узловой вектор, вектор контрольных точек и вектор весов. Этого достаточно для однозначного задания сплайна. Задача решена.
Как мы могли видеть, алгоритм продления рационального NURBS в сущности такой же, как и для нерационального, только требует некоторых дополнительных шагов. Изобразим исходный и продленный сплайны на картинке (см. Рис. 6).
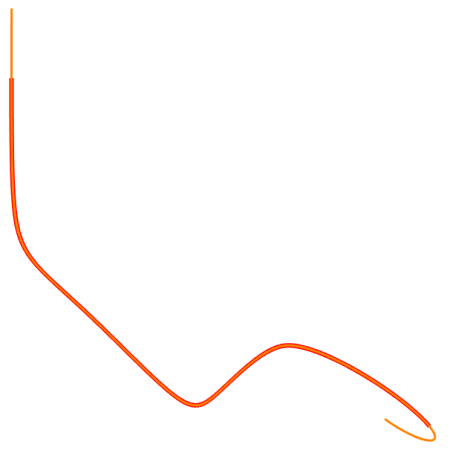
В заключение хотелось бы отметить, что любой NURBS (как рациональный, так и нерациональный) «распрямляется» (кривизна стремится к нулю) в бесконечности. Этот факт имеет строгое математическое доказательство, но его мы оставим за рамками данной статьи. Покажем только, как проявляется данный эффект при продлении цилиндрической спирали, преобразованной в NURBS. На первый взгляд может показаться, что продленная кривая должна описывать дополнительные витки спирали, но на практике получаем нечто иное (см. Рис. 7).
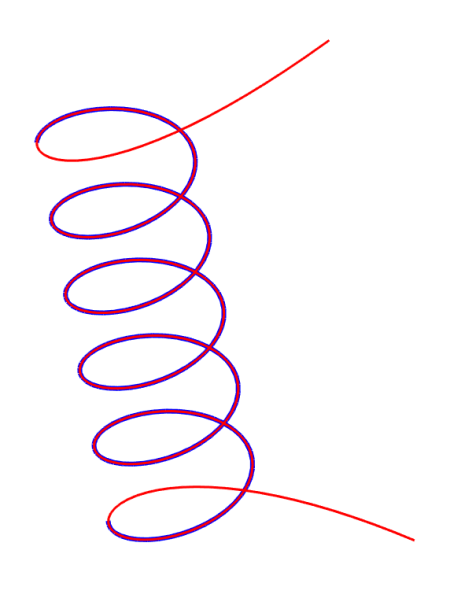
Синяя – исходная кривая (NURBS из цилиндрической спирали), красная – продленная
Заключение
Описанный выше функционал продления кривых был реализован по запросам пользователей, поэтому в данной статье мы постарались избежать громких рассуждений о его сложности и важности. Просто внедрили — и все.
Естественно, мы не описали всех нюансов и подробностей, с которыми мы столкнулись при его реализации. Был описан алгоритм продления только NURBS‑кривых, но в реальности пришлось покрывать множество других типов кривых различными частными случаями.
У самого алгоритма существуют вполне реальные пути для развития. Тем не менее сейчас он готов к использованию пользователями ядра C3D и приложения KOMPAS-3D (там он тоже уже реализован и функционирует). Полагаем, что в будущем (с течением времени) он будет только совершенствоваться.
Список литературы
Н. Н. Голованов, ГЕОМЕТРИЧЕСКОЕ МОДЕЛИРОВАНИЕ, ДМК Пресс, 2019.
L. Piegl and W. Tiller, The NURBS Book, Springer-Verlag, 1997.

Николай Бухалов
Математик-программист C3D Labs


1eternal
почему ваш просмотрщик не скачать?
им же можно бесплатно пользоваться.
заполнил форму, жду письма, чтобы подтвердить учётку и ничего.
это так и задумано?
типа вот бесплатный просмотрщик, но скачать мы вам его не дадим
c3dlabs Автор
Добрый день, на сайте C3D Labs ведутся технические работы. Совсем скоро вы сможете скачать бесплатную версию Viewer для вашего использования.