Привет, Хабр! В этой статье мы рассмотрим один из подходов к офлайновому A/B-тестированию, поговорим о сложностях, которые возникают при оценке результатов пилотного проекта (далее — пилота) и разберём реализацию в коде.

В Сбербанке постоянно проводится много пилотов, часть из которых реализуются в сети продаж Банка (отделения, банкоматы) и требуют нестандартного подхода к оценке результатов. Примеры таких пилотов:

• введение новой роли сотрудника в отделениях Банка;

• различные мероприятия с отделениями (открытие, закрытие или перемещение офиса);

• предложения услуг клиентам в локациях, оценка коммуникации;

• тестирование в офисе новых идей, продаж новых продуктов и влияния поводов.

Есть несколько причин, которые требуют применения нестандартного подхода к исследованиям. Во-первых, это небольшая выборка, которая не позволяет посчитать статистическую значимость результата и сделать вывод. Например, некоторые пилоты могут проводиться в нескольких офисах, а оценку требуется дать исходя из имеющихся фактических данных.

Во-вторых, отделения Сбербанка расположены в различных уголках нашей страны, что создаёт проблему неоднородности данных. Также влиять на результат оценки пилота может и поведение клиентов, их профиль и портфель банковских продуктов.

В-третьих, мы не можем использовать в А/В тестировании стандартный подход и быть уверенными в качестве разбиения, так как не можем заранее разбить на две независимые группы, из-за чего часто приходится подбирать контрольную группу к целевой Подробнее об этом читайте в нашей предыдущей статье.

Один из способов решения указанных проблем — переход на клиентский уровень при оценке пилотов. Например, если требуется оценить успешность предлагаемого изменения процесса в отделении, то сделать это можно по изменению операционного дохода между группами клиентов, а не только по результатам работы всего отделения. 

До запуска пилота необходимо определить:

• критерии его успешности;

• дополнительные метрики для отслеживания ситуации;

• чёткие критерии отбора клиентов в целевую группу;

• и критерии подбора к целевой группе клиентов контрольной группы.

После завершения пилота необходимо сформировать в соответствии с выбранными критериями целевую и контрольную группы клиентов для оценки результатов. Для этого можно выделить отделения с изменённым процессом (целевая группа) и его исходным вариантом (контрольная группа), и далее сравнивать клиентов этих групп. 

Но при этом стоит учитывать особенности формирования групп, а именно:

• клиенты из контрольной и целевой групп должны быть «похожи» друг на друга;

• клиенты из контрольной и целевой групп должны быть из одного населённого пункта (или региона).

Соблюдение этих условий необходимо для однородности данных и возможности интерпретировать разницу результатов между группами как эффект от проведения пилота, потому что иначе мы можем получить некорректные результаты.

В Data Science существует ряд задач, которые предусматривают поиск похожих объектов, как, например, поиск похожих профилей пользователей, подбор схожей музыки или рекомендации похожих товаров. Задачу подбора похожих клиентов можно решить, как и вышеуказанные, сведя её к преобразованию характеристик профиля клиента в векторную форму и поиску ближайших ему векторов. Для подбора клиентов можно использовать одну из мер «сходства»:

1. Евклидово расстояние (L2, Euclidean distance)

Наиболее распространённая мера расстояния, которую проще всего интерпретировать как длину отрезка, соединяющего две точки. Формула довольно проста, так как расстояние рассчитывается по картезианским координатам точек с использованием теоремы Пифагора.

Недостатки:

• Данные должны быть предварительно нормализованы.

• «Проклятие размерности», или снижение полезности этой метрики по мере роста размерности пространства.

2. Манхэттенское расстояние (L1, Manhattan distance)

Метрика, которую ещё называют расстоянием городских кварталов, определяет расстояние как сумму модулей разностей их координат.

Метрика может применяться для расчёта расстояний в многомерном пространстве.

3. Косинусное сходство (Cosine Similarity)

Эта мера, в отличие от Евклидова расстояния, работает в многомерном пространстве. Согласно формуле, это просто косинус угла между векторами, нормализованный на произведение их длин. Два вектора с одинаковой ориентацией имеют косинусное сходство 1, тогда как два вектора, диаметрально противоположные друг другу, имеют сходство -1.

К недостаткам можно отнести то, что эта мера не учитывает размер вектора, а только направление. Мера широко распространена в рекомендательных системах и в работе с текстами.

4. Расстояние Хэмминга (Hamming distance)

Это количество позиций, в которых соответствующие значения двух векторов одинаковой длины различаются. Как следует из определения метрики, она не учитывает значения векторов, кроме того, что они различаются или равны.

5. Расстояние Махаланобиса (Mahalanobis distance)

Метрика обобщает понятие Евклидова расстояния. По сути, она похожа на Евклидово расстояние, но в неё заложен дополнительный смысл: чем ближе точка к «центру масс», тем вероятнее, что это нужная нам точка.

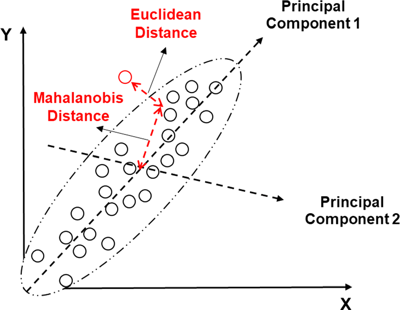
Каждая из этих мер имеет свои особенности, и от вашего выбора будет зависеть конечный результат. Одним из вариантов решения задачи подбора похожих клиентов является мера косинусного сходства (cosine similarity), реализацию которой можно найти, например, в пакете scipy.spatial.distance.

Ранее мы использовали Python-библиотеку Сausalinference и искали похожих клиентов по метрике Махаланобиса. Но этот способ оказался слабо оптимизированным для больших данных, когда понадобилось искать похожих клиентов на миллионных выборках. Поэтому мы начали искать более быстрые и качественные подходы.

Для подведения итогов пилота необходимо по одной из вышеуказанных метрик подобрать для каждого клиента целевой группы исследования несколько других клиентов в пределах одного населенного пункта, посчитав выбранную для оценки меру «сходства». Для ускорения расчётов также можно предварительно рассчитать витрину со схожими клиентами для всей клиентской базы. Это позволяет быстро оценить пилот на клиентском уровне, сделав несколько запросов к базе данных.

Витрину можно построить в два этапа:

1. Сначала формируем временную витрину с клиентами, которые посещали офис в течение заданного временного периода. Для каждого клиента определяем все релевантные офисы на основе частоты визитов, а затем рассчитываем эмбеддинги на основе признаков клиента и его транзакций с помощью фреймворка Pytorch-Lifestream.

2. На втором этапе итеративно ищем для каждого клиента двух-трёх похожих на него. Похожесть между двумя векторами клиентов определяем с помощью выбранной метрики расстояния.

Поиск похожих клиентов для всех отделений в РФ

Исходя из объёма клиентской выборки Сбербанка, становится понятно, что эта задача очень дорогая в вычислительном плане. Есть несколько подходов к расчёту витрины с помощью трёх различных подходов.

Apache Spark

Первый способ решения — расчитать «в лоб», с помощью тяжёлой артиллерии — кластера Spark с большим общим объёмом памяти (порядка 1-2 ТБ). Технически это выглядит следующим образом:

• Выполняем cross join таблицы с клиентами и их векторными представлениями на саму себя.

• Расчитываем попарную метрику сходства по всем клиентам.

• Ранжируем результаты по метрике близости (в верху списка располагаются самые близкие векторы) с помощью оконной функции.

• Фильтруем данные: выбираем по три самых близких (похожих) клиента.

Очевидно, что такой способ неоптимален с точки зрения вычислительных затрат, потому что выполняется cross join двух таблиц. Он сильно уступает другим, в том числе наилучшим подходам в области методов приближенного поиска ближайших соседей.

Facebook FAISS

Одна из современных библиотек для поиска ближайших соседей — FAISS от Facebook Research, которая содержит несколько методов для поиска сходства. Её идея в разбиении векторного пространства на области с помощью метода k-means и присвоении каждой опорной точке (центроиду) соответствующей области списка векторов.

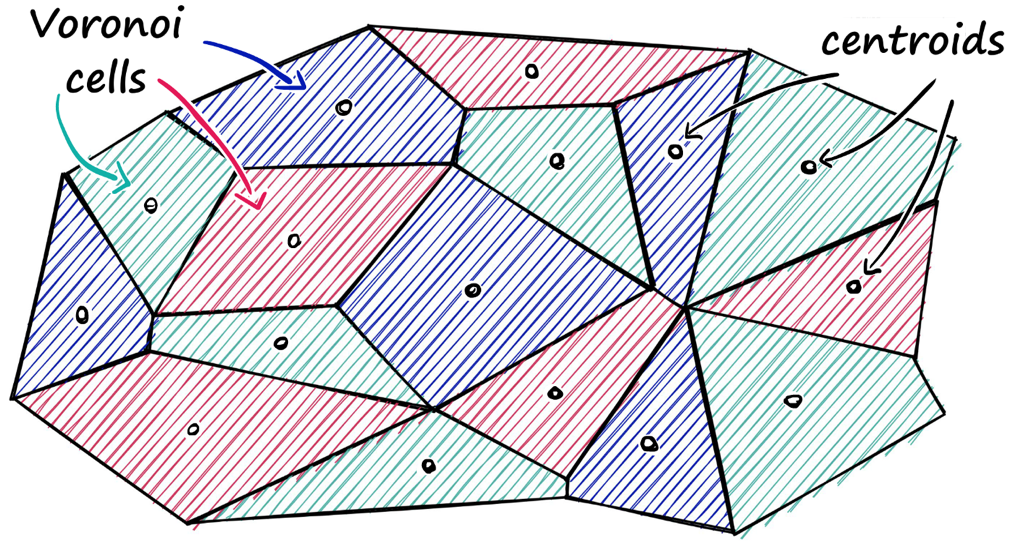
Неоспоримое преимущество этой библиотеки заключается в возможности использовать GPU для построения индекса и поиска ближайших соседей. Для этого необходимо в коде заменить IndexFlatL2 на GpuIndexFlatL2, при этом скорость расчёта возрастёт на порядок. Подход, реализованный с помощью FAISS, обычно работает быстрее реализации на Spark.

Spotify Annoy

Поиск похожих клиентов с помощью библиотеки Annoy от Spotify происходит с помощью рекурсивного разделения векторного пространства плоскостями, в результате чего образуется бинарное дерево. 

В каждом узле дерева хранится вектор, задающий текущую плоскость. Поиск ближайшего вектора начинается с корня (root node), далее выбирается дочерний лист на основе положения запроса относительно плоскости. Таким образом, спускаясь по бинарному дереву мы останавливаемся в листе, в котором хранятся векторы, ближайшие к вектору-запросу.

Стоит отметить высокую скорость работы алгоритма при поиске похожих клиентов.

Выбор алгоритма 

Тестирование качества этих алгоритмов подбора похожих клиентов на случайной выборке, с достаточно хорошим и полным набором клиентских признаков, показывает релевантность результатов.

Чтобы понять, является ли новый метод лучше используемого ранее, необходимо обращать внимание на следующие факторы:

• Скорость поиска похожих. Метод может быть очень хорошим с точки зрения равенства метрик, но если для его запуска на большом количестве клиентов приходится ждать слишком долго, это может занять повлиять на бизнес-планирование и, в конечном итоге, снизить ценность поиска похожих.

• Качество подбора похожих. Предположим, мы подобрали похожих клиентов, но как оценить эффективность такого подбора? Нам необходимо взять группы клиентов (целевую и контрольную), и проверить поведение до пилота. Если подбор выполнен качественно, до пилота не должно быть смещений по ключевым метрикам. Также мы должны проверить статистические распределения интерпретируемых признаков по клиентам. Даже если мы используем эмбеддинги, мы должны быть уверены, что основные признаки распределены похожим образом.

Заключение

Решение нашей задачи позволяет:

• Изучить подходы по обучению нейросетевых моделей для получения эмбеддингов клиентов.

• Автоматизировать оценку пилотов на клиентском уровне, проводимых в сети продаж Сбера.

• Значительно сократить время на оценку пилотов.

• Исследовать различные подходы и выбрать лучший алгоритм.

Задачи по быстрому поиску в многомерном векторном пространстве актуальны, и наличие готовых open source-решений позволяет быстрее проводить эксперименты и реализовывать бизнес-задачи.

Авторы: Александр Литвинцев, Максим Сунгоркин, Александр Поляков, Ян Скуковский