Приветствую Вас, уважаемые Читатели! Сегодня я хочу рассказать Вам о замечательном популяризаторе математики Чарльзе Говарде Хинтоне - человеке, внесшем просто огромный вклад в дело изучения объектов четырехмерного мира.
Зачем, спрашивается, их изучать? Я, для начала, ограничусь цитатой его тезки Говарда Лавкрафта, произведения которого я не так давно очень полюбил:

Что знаем мы об этом мире и о Вселенной? — говорил он. — У нас до абсурдного мало органов чувств, а наши представления об окружающих предметах до невероятного скудны. Мы видим вещи такими, какими мы созданы их видеть, и мы не в состоянии постичь абсолютную их суть. Со своими пятью жалкими чувствами мы лишь обманываем себя, иллюзорно представляя, будто воспринимаем весь безгранично сложный космос - "Из глубин мироздания (1934)".
Говард Хинтон - человек с удивительно интересной биографией, но главной заслугой всей его жизни был цикл книг, посвященных пространству. Начиная с простых примеров на прямой и плоскости, Хинтон уводит читателя к объектам трехмерным, а уже затем "подкидывает" нас уже отработанными методами в мир четырехмерный.

В течение своей жизни Хинтон разрабатывал оригинальные методы, с помощью которых не только профессиональные математики, но и любой среднестатистический человек из числа растущих рядов его последователей мог бы «увидеть» четырехмерные объекты. Наконец Хинтон усовершенствовал специальные кубы, которые при условии приложения достаточных стараний помогали визуализировать гиперкубы, или кубы в четырех измерениях.

Они получили название «кубы Хинтона». Хинтон даже ввел в обращение официальное название развертки гиперкуба — тессеракт, которое прижилось в английском языке. Давайте рассмотрим подробнее, что же придумал математик. Одним из способов визуализации объектов высших измерений является их пересечение с объектами с меньшей размерностью. Например, возьмем трехмерный куб и пропустим его через двумерную плоскость:

Очевидно, что мы увидим одну из граней куба, а за три прохода - сможем рассмотреть их все, если до этого каким-то образом пометим каждую грань. Именно такой ход и задумывает Хинтон, чтобы визуализировать тессеракт. Если гиперкуб проходит через наше трехмерное пространство, мы могли бы воспринять его трехмерное сечение. Окраска кубиков Хинтона основана на сопоставлении четырех измерений с четырьмя цветами: красным, желтым, синим и белым. Когда точка тессеракта перемещается по измерению, цвет этого измерения добавляется к исходному цвету точки. Конечный цвет - это результат смешивания. Это смешение дает в общей сложности шестнадцать цветов:

Теперь проследим путь какой-либо точки гиперкуба, чтобы понять принцип формирования цветов его граней. Предположим, что у нас есть точка "без цвета", которая перемещается в пределах желтого измерения x. Результатом будет отрезок линии желтого цвета. Давайте предположим, что эта движущаяся точка начинается и заканчивается начальным цветом и что внутренние точки окрашены в цвет измерения. Таким образом, у нас есть отрезок линии, имеющий конечные точки "нулевого цвета" и желтые внутренние точки:

Отрезок будет перемещаться в пределах "красного" перпендикулярного измерения y. Конечные и начальные точки исходного отрезка будут двигаться в это измерении, оставляя красный след, а грань получившегося квадрата станет желтый+красный = оранжевой!

Теперь переместим этот квадрат в третьем измерении z, которое обозначается синим цветом:

Верхняя грань: синий+желтый = зеленый;
Грань справа: красный + синий = фиолетовый;
Внутренние грани: красный + желтый + синий = коричневый (в соответствии с измерениями, в которых мы двигали наши фигуры!)
Собрав воедино все возможные движения таких точек, можно построить следующую диаграмму:

Теперь осталось реализовать приемы пересечения с объектами низших измерений. Пропуская кубы Хинтона через плоскость мы получим, например:

Но наиболее интересной будет визуализация самого гиперкуба. У нас будет четыре варианта, в которых гиперкуб проходит через наше пространство, начиная с одной кубической грани куба Хинтона и заканчивая противоположной (аналогично окрашенной) гранью, а все грани будут иметь дополнительный цвет в зависимости от измерения, отсутствующего в трехмерном пространстве:
Если куб имеет желтые, белые и красные грани, будет добавлен синий цвет.
Если куб имеет желтые, синие и красные грани, будет добавлен белый цвет.
Если он имеет синие, красные и белые грани, то будет добавлен желтый цвет.
Если он имеет желтые, белые и синие грани, то будет добавлен красный цвет.

Разберем для примера первую строку: 1. Точка без цвета двигается вправо в белом измерении - получаем белый отрезок. 2. Отрезок движется в красном измерении - получаем квадрат с розовой гранью (белый + красный). 3. Квадрат движется в желтом измерении - получаем куб. 4. Теперь устремляем гиперкуб в четвертом измерении (а это отсутствующий синий цвет!)

На выходе гиперкуб "выворачивается" к нам первоначальной стороной. На самом деле изготовить кубики Хинтона и "поиграться в натуре" можно и самому, затратив на это некоторые усилия:

Кубы Хинтона широко рекламировались в женских журналах и даже применялись на спиритических сеансах, где вскоре приобрели мистическое значение. Представители высшего общества утверждали: медитируя на кубах Хинтона, можно уловить проблески четвертого измерения, а значит, и потустороннего мира духов и умерших близких. Его ученики часами изучали эти кубы, медитировали на них, пока не приобретали умение мысленно переставлять и разбирать эти кубы посредством четвертого измерения, получая гиперкуб. Высказывалось утверждение, будто бы тот, кто справляется с этой умственной задачей, способен достичь высшего состояния — нирваны.

Сам Хинтон после публикации материалов о четвертом измерении жил довольно размеренной и успешной жизнью, пока не был арестован (внезапно, отец Хинтона, Джеймс Хинтон, был хирургом и сторонником полигамии) за двоеженство и был вынужден отправиться в Японию, где работал учителем. Переехав через несколько лет в Северную Америку, Говард работал во многих университетах и всё так же увлеченно рассказывал научному сообществу и простым гражданам о четвертом измерении.

Надо сказать, довольно успешно. Например, в романе Герберта Уэллса «Машина времени» (1895) Путешественник рассуждает о природе четвёртого измерения прямым текстом из рассказа «Незавершённая связь» второго сборника Хинтона (1895). Великий Хорхе Луис Борхес вообще включил произведения Хинтона в свою "вавилонскую библиотеку" и несколько раз упоминал англичанина в своих коротких, но глубоких рассказах. Ушел в "четвертое измерение" Хинтон внезапно - от кровоизлияния в мозг. За ним, чуть меньше, чем через год последовала супруга, наложив на себя руки. Через год после их смерти в 1908 году немец Герман Минковский впервые математически строго определит четырехмерное пространство-время...впрочем, это уже совсем другая история.
Больше математики в Telegram - "Математика не для всех"
Комментарии (20)

Popadanec
09.04.2023 05:31+2Мне как то даже фантастика попадалась, где человек решил построить дом такой формы, этот дом свернулся в куб после постройки, но внутренний объём остался. Окна вели то ли в разные части света, то ли в разные миры, уже не помню.

nwanomaly
09.04.2023 05:31+1Я этот рассказ в детстве читал или в ЮТ, или в ТМ. Даже из шариков и палочек тогда сделал тессеракт, как в том рассказе был )

CaptainFlint
09.04.2023 05:31+6"Дом, который построил Тил" Р. Хайнлайна (—And He Built a Crooked House—)

perfect_genius
09.04.2023 05:31О, подходящая тема спросить, давно хотел узнать.
Я правильно понимаю, что что внутренний куб в тессеракте — это, условно, координата 1 четвёртого измерения, а координаты 2, 3 и далее до бесконечности будут уже внутренними кубами внутри каждого следующего внутреннего куба? Координата 0 — это текущий внешний куб, -1 будет уже куб побольше, в котором окажется этот текущий куб…
Т.е. будто линейка идёт бесконечно в центр тессеракта.
venanen
09.04.2023 05:31У тессеракта нет внутреннего куба. И внешнего. У куба в трехмерном пространстве же нет внутренних квадратов? Выше уже скидывали ссылку на видео @Onigiri, продублирую с таймкодом: https://youtu.be/1fQVnpwn1fA?t=542

perfect_genius
09.04.2023 05:31+1А вот эти цветные линии и стороны из статьи, значит, есть?
Внутренний куб — это же условность. Этот куб — это условная координата 1 же?
VPryadchenko
09.04.2023 05:31Это гипер-грань, которая находится сзади. Вы когда куб на плоскости изображаете, тоже рисуете "квадрат внутри" - аналогичная штука.

CaptainFlint
09.04.2023 05:31+3Приведённая картинка — это искажённая проекция гиперкуба на трёхмерное пространство. Так же как обычный трёхмерный куб можно изобразить на плоскости в виде:
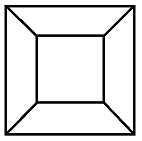
"Внешний квадрат" — это одна грань, "внутренний" — противоположная. Так же и с гиперкубом: "внешний куб" — одна грань гиперкуба, "внутренний" — другая грань, противоположная первой. Продлить четвёртую координату дальше, разумеется, можно. В соответствии с правилами выбранного типа проекции она будет бесконечно стремиться к центру, всё уменьшаясь и уменьшаясь в масштабе. Но там не будет никаких дополнительных "внутренних кубов". Мы уже вышли за пределы гиперкуба по этой координате, дальше ничего нет. Разве что мы хотим нарисовать цепочку гиперкубов, стоящих друг за другом вдоль четвёртой координаты, тогда да, в такой проекции они будут выглядеть как вложенные всё уменьшающиеся до бесконечности кубики.

iShrimp
09.04.2023 05:31+3Вообразив тессеракт, можно приступать к следующему упражнению - вообразить гиперсферу (4-мерную 3-сферу) и 3-мерное сферическое пространство, что гораздо сложнее...

Andreadful
09.04.2023 05:31У Хайнлайна есть рассказ "Дом, который построил Тил" про вот это самое – про тессеракт.

tormozz48
09.04.2023 05:31Есть кстати еще занимательный рассказ Роберта Шекли: "Мисс Мышка и четвертое измерение" - про то как человек как раз сошел с ума складывая в голове все эти кубы



N-Cube
На самом деле, все интереснее. Пространство Минковского обладает псевдоевклидовой метрикой Лоренца (с точностью до знака - можно инвертировать), так что определение метрики уже существовало (да и в целом, знакопеременные метрики давно были известны), оставалось увязать такую метрику с пространством-временем. Поэтому математическое определение метрического тензора (и его преобразований) авторства Лоренца, а вот его применение (пространство) авторства Минковского. А если еще добавить результаты Пуанкаре, то Эйнштейну ничего не оставалось, как придумать практическое применение всей этой математики - теорию относительности :)