Приветствую Вас! Сегодня мы поговорим об интересной кривой, у которой есть своё название — суперэллипс.
Оглянитесь вокруг. Какие фигуры вы видите? Скорее всего, большинство фигур имеет либо прямые (острые, тупые) углы либо эллипсоидные (не всегда идеально круглые) границы. Однако, существуют и гибриды. Суперэллипсы — это семейство кривых, которые лежат где‑то между эллипсами и прямоугольниками.
Для начала вспомним, что из себя представляет обычный эллипс — кривую второго порядка:

Коэффициенты a и b определяют «приплюснутость» эллипса по горизонтали и вертикали соответственно:
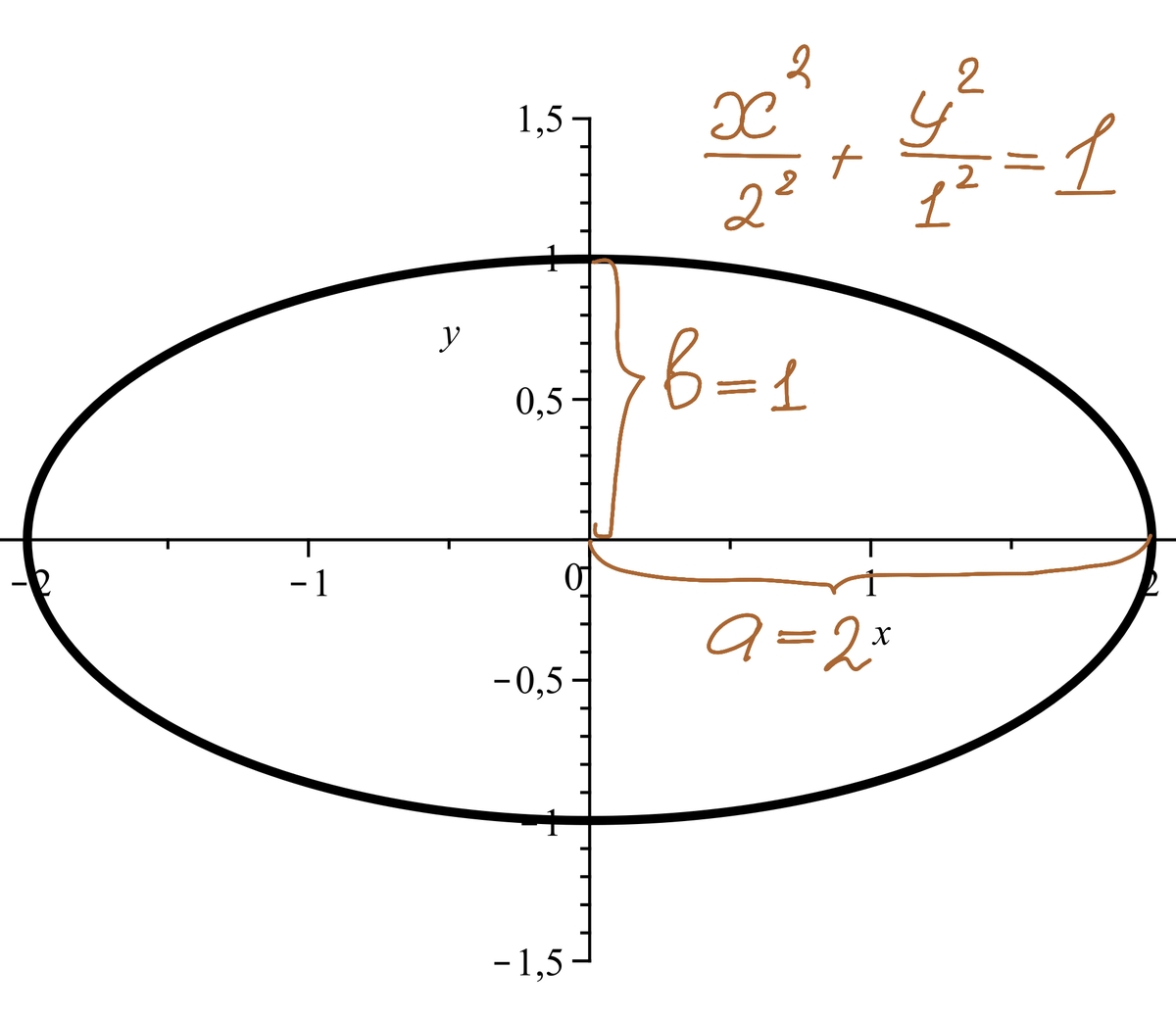
Но что, если вторые степени заменить чем‑то другим? Если возвести в куб, в четвертую степень и т.д?
В 1959 году в шведском Стокгольме был объявлен конкурс на проектирование кольцевой развязки одной из городских площадей. Этот район находился там, где две широкие магистрали пересекались в центре города, поэтому требовалось не перекрыть транспортные потоки, да еще и обеспечить пешеходную зону уровнем ниже:

Архитектор Пит Хейн искал наиболее эстетичную, но и эффективную форму, о чем писал:
Человек — это животное, которое рисует линии, о которые он сам потом спотыкается. Всегда цивилизации наблюдались две тенденции: одна — к прямым линиям и прямоугольным узорам, а другая — к круговым линиям. Для обеих тенденций есть причины, механические и психологические. Вещи, сделанные с помощью прямых линий, хорошо сочетаются друг с другом и экономят место. И мы можем легко перемещаться — физически или мысленно — по предметам, сделанным с круглыми линиями.
Но мы в смирительной рубашке, вынуждены принимать то одно, то другое, когда часто какая‑то промежуточная форма была бы лучше. Рисовать что‑то от руки — например, многоуровневое дорожное кольцо, которое они пробовали в Стокгольме, — не годится. Суперэллипс решил проблему. Он не круглый и не прямоугольный, а что‑то среднее. Тем не менее, она фиксирована, она определенна — в ней есть единство.
Уравнение суперэллипса в общем виде записывается следующим образом:

В зависимости от соотношения параметра n можно получить целую россыпь фигур.
Когда n приближается к нулю, кривая вырождается в две прямые пересекающиеся линии вдоль осей.
При 0<n<1 получаете ромб с вогнутыми сторонами.
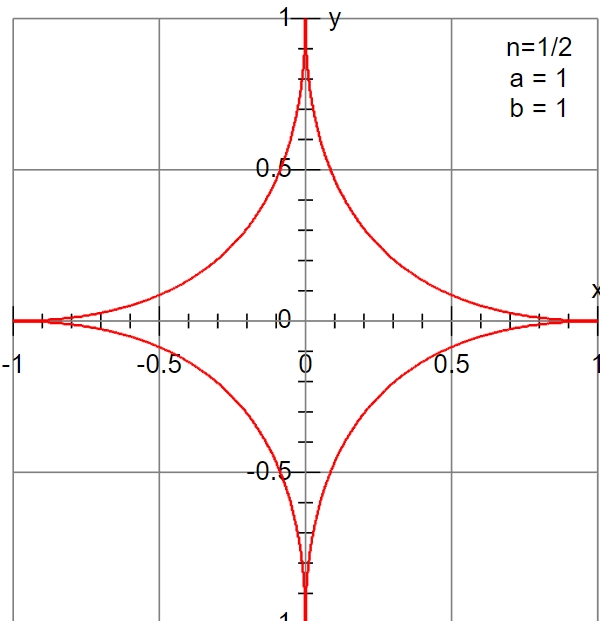
Когда n = 1, вы получаете ромб с вершинами на осях координат.
При 1<n<2 получаете ромб с выпуклыми сторонами.

Когда n = 2, вы получаете эллипс (или, если a и b равны - окружности).
Если значение n > 2, у вас получается суперэллипс. (при проектировании площади, о которой я говорил выше, использовался параметр 2,5).
По мере приближения n к бесконечности получаем прямоугольник.

Стоит отметить, что, хотя суперэллипсы могут выглядеть так, как будто у них прямые стороны, соединенные кривыми, на самом деле они изогнуты по всему периметру. Даже там, где сегмент выглядит прямым, он на самом деле слегка изогнут, а кривизна изменяется повсюду непрерывно.
Если вы повернете суперэллипс вокруг главной оси, получится суперяйцо, которое устойчиво относительно своих биологических аналогов:
Форму суперэллипса имеют архитектурные объекты, предметы интерьера, логотипы брендов и команд:

Однако подавляющее число людей впервые увидело суперэллипс...когда взяли в руки Iphone! Дело в том, что начиная c шестой версии iOs, дизайнеры перестали использовать прямоугольники с закруглением, а перешли к суперэллипсам:


По ощущениям здесь используется суперэллипс с коэффициентом n = 5..7. Если и этого недостаточно, то знайте, что супСуперэллипс — фигура, которую многие видят каждый день, но не догадываются об этомерэллипс фигурировал в статье «Геометрическое моделирование и гидродинамический анализ плавающих сперматозоидов», жаль только, что этой публикации нет в открытом доступе.
Больше математики в Telegram - "Математика не для всех"
Комментарии (21)

IosifLvovich
12.04.2023 05:22+47Однако подавляющее число людей впервые увидело суперэллипс...когда взяли в руки Iphone!
Серьёзно? Неужели чувство уникальности яблофилов настолько потускнело, что приходится подобную ахинею городить?

nick-for-habr
12.04.2023 05:22+31Не первый раз уже встречаю (скорее всего и на Хабре было) про эти "суперэллипсы", и всегда — в связке с оЙфонами.
Мол такой Эппол весь из себя научный, провёл кучу исследований, чуть ли не новое направление в геометрии открыл, и всё для того, что бы его иконки были самые лучшие и "не такие как все".
Боже ж мой, да всем пофиг на форму иконок. Большинство не отличит оЙфон от Андроида, если стереть лейбл с корпуса и не сказать цену телефона.
Но надо же что-то впаривать. Видимо совсем ничего не осталось, раз про "круглые углы" вспомнили.
После выхода каждой новой модели оЙфона с очереднымбесполезныминновационным "датчиком сердцебиения" нам несколько раз настойчиво пихают в СМИ слезливые истории, как этот вот самый датчик "спас семью квир-афроамериканцев из Пенсильвании", отправив сигналсамому Стиву Джобсунапрямую в полицию. А в предыдущей модели "датчик содержания кислорода" спас "маленькую девочку из Огайо" от страшной опухоли. А ведь всего этого могло бы и не быть, если бы Эппол как и все использовала обычные банальные "круглые углы", а не инновационные "суперэллипсы".
А хотите знать настоящую причину? Это моё предположение, но зная Эппол — мне оно кажется правдоподобным.
Просто "круглые углы" в иконках уже использовались ранее, и их нельзя было запатентовать. А вот "суперэллипсы" — почти такие же, но не такие. И они 100% запатентованы Эпполом как элемент интерфейсаоЙфоноввсего.
Всё просто: ищите кому выгодно.
kahi4
12.04.2023 05:22+2Да ладно. На самом деле все гораздо проще. Apple просто любит нанимать людей с опытом или фанатизмом в промышленном дизайне, а там то что нужно избегать резкого перехода из прямой в круг известно давно и связано с тем как ведут себя отражения на переходе (они разрываются в этом месте и это выглядит некрасивой прямой линией). В пром дизайне избегание этого вполне естественно, а Apple любит тащить от туда идеи (взять хотя бы калькуляторы braun).
(Ну и что-то что-то, аэродинамика, Бизье, что-то что-то).
Мне понравилось это видео на эту тему (на английском) https://www.youtube.com/watch?v=jvPPXbo87ds&t=3965s (не про apple, а про кривые и их свойства. И вообще блог про гейм дев), но там хорошая визуализация проблемы.

dom1n1k
12.04.2023 05:22+1Эта версия хороша, но несколько не стыкуется с тем фактом, что нигде в яблочной документации не указаны параметры этого суперэлипса.
То есть мы такие прошаренные фанаты и перфекционисты, но точный контур вам не скажем. Формулы нет нигде. В публичном доступе только картинка, которая показывает — "ну вот примерно как-то так, а подробности не вашего ума дело".
kahi4
12.04.2023 05:22+2Ой да ладно. Я имел ввиду что в пром дизайне часто избегают разрыва производной, но никто не скажет как именно, потому что это их «фишка».
Ну а от Apple ожидать какие-то детали это как от кока колы ожидать состав на банке.
К слову, отсутствие точной формулы так же разрушает идею патента, покуда там она должна быть.

ssj100
12.04.2023 05:22+2Просто сделали минимальные изменения чтоб глаз цеплялся за не идеальную картинку…
Мне всегда казалось что с иконками IOSи что-то не так. Так и для остальных наверное такую тайну/шарм на подкорке оставляют и цепляют
Что для маркетологов и нужно.

Didimus
12.04.2023 05:22Ну не знаю. Мне видится суперэллиптичное яблоко поприятнее, чем квадратное.

nick-for-habr
12.04.2023 05:22Кто-то любит котлетки, а кто-то — кухарку. Это нормально.
Хорошо что на Android можно любую форму для иконок выбрать: и квадратные, и суперэллиптические, и просто круглые, и в ромбиках, и "звёздочками" — что нравиться, то и используешь.
На iPhone наверное выбор ещё больше — не даром говорят же, что они гораздо лучше устройств на Android.
Так и должно быть: у пользователей должна быть возможность использовать то, что им нравится.

Kenya-West
12.04.2023 05:22чем квадратное
Тем временем Windows Phone и Metro UI в частности - образец отличного дизайна. Правда, дизайна своего времени, потому что обмылочный мир в итоге победил

KvanTTT
12.04.2023 05:22+1Что-то я визуально не различил суперэллипс от прямоугольного со скругленными углами. Если отличия и есть, то очень плохо различимые. Можно что-нибудь понаглядней?

burz_ex
12.04.2023 05:22+1Визуально действительно сложно разделить. Но в целом идея в том, что прямоугольник имеет участки периметра с прямыми, а эллипс всегда с изгибом.

Refridgerator
12.04.2023 05:22+2Математической составляющей могло бы быть и побольше. Например: определение суперэллипса в полярных координатах, через функцию вида y=f(x), через координату угловой точки, площадь, длину кривой, функцию кривизны в явном виде...



Jianke
Круто!