Автор статьи: Артем Михайлов

Марковские цепи — это математическая модель, которая с успехом применяется в различных областях, таких как машинное обучение, генерация текстов или музыки, криптография и многих других. Модель была разработана Андреем Марковым в начале 20 века и с тех пор нашла широкое применение в различных областях.

Андрей Андреевич Марков — выдающийся российский математик, работавший в области вероятностных процессов, теории чисел и математической статистики. Одной из его самых известных работ является разработка математической модели, получившей название «Марковские цепи».



Термин был впервые введен в 1906 году в статье «О предельном распределении одного класса связанных случайных величин», где он изучал статистическое поведение цепочки взаимосвязанных случайных событий.

Суть модели заключается в том, что она позволяет предсказывать вероятность перехода из одного состояния в другое на основе текущего состояния. Таким образом, на основе математической модели Марковской цепи можно генерировать последовательности, являющиеся словами, музыкальными фрагментами, программным кодом и т.д.

Особенно интересным применением Марковских цепей является их использование в области компьютерной графики и киноиндустрии. Благодаря этой модели можно сгенерировать реалистичные анимации и эффекты спецэффектов в кино. Также Марковские цепи используются в обработке естественного языка и генерации текстов.

В данной статье мы рассмотрим основы Марковских цепей, а также реализуем Марковские цепи на Python.

Основные термины

Конечный автомат (Finite State Machine, FSM) – это математическая модель, состоящая из ограниченного числа состояний, множества допустимых входов, переходов между состояниями и конечного числа выходов. FSM используется в информатике, чтобы представлять группу объектов или системы и следить за их поведением.



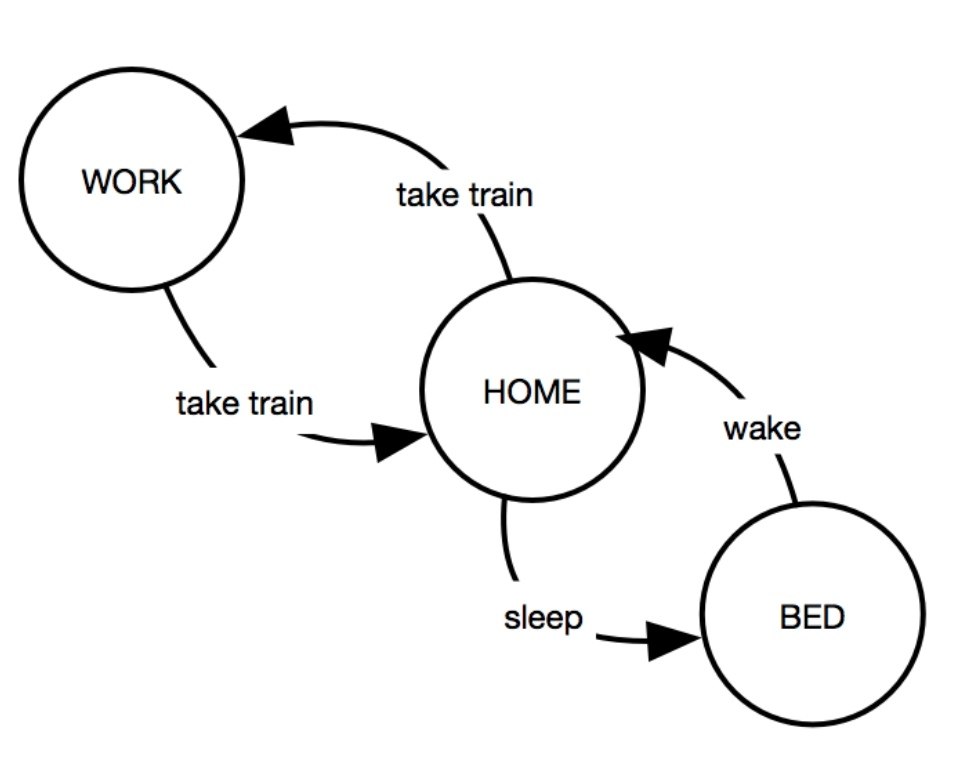
В Марковских цепях FSM моделирует последовательность состояний.

Случайный процесс — это математический объект, используемый для моделирования случайных явлений. Примеры случайных процессов включают случайное блуждание и процессы Пуассона. Марковские цепи являются примером случайного процесса, в котором вероятность перехода из одного состояния в другое зависит только от текущего состояния системы.

Стационарное распределение — это распределение, которое система принимает после бесконечного количества переходов. Это означает, что вероятности перехода не изменяются с течением времени и система стабилизируется. Стационарное распределение позволяет определить, какую вероятность имеет каждое состояние системы в долгосрочной перспективе.

Вероятность перехода — это вероятность того, что система перейдет из одного состояния в другое. В каждой точке времени система может перейти в другое состояние с определенной вероятностью, которая определяется текущим состоянием системы.



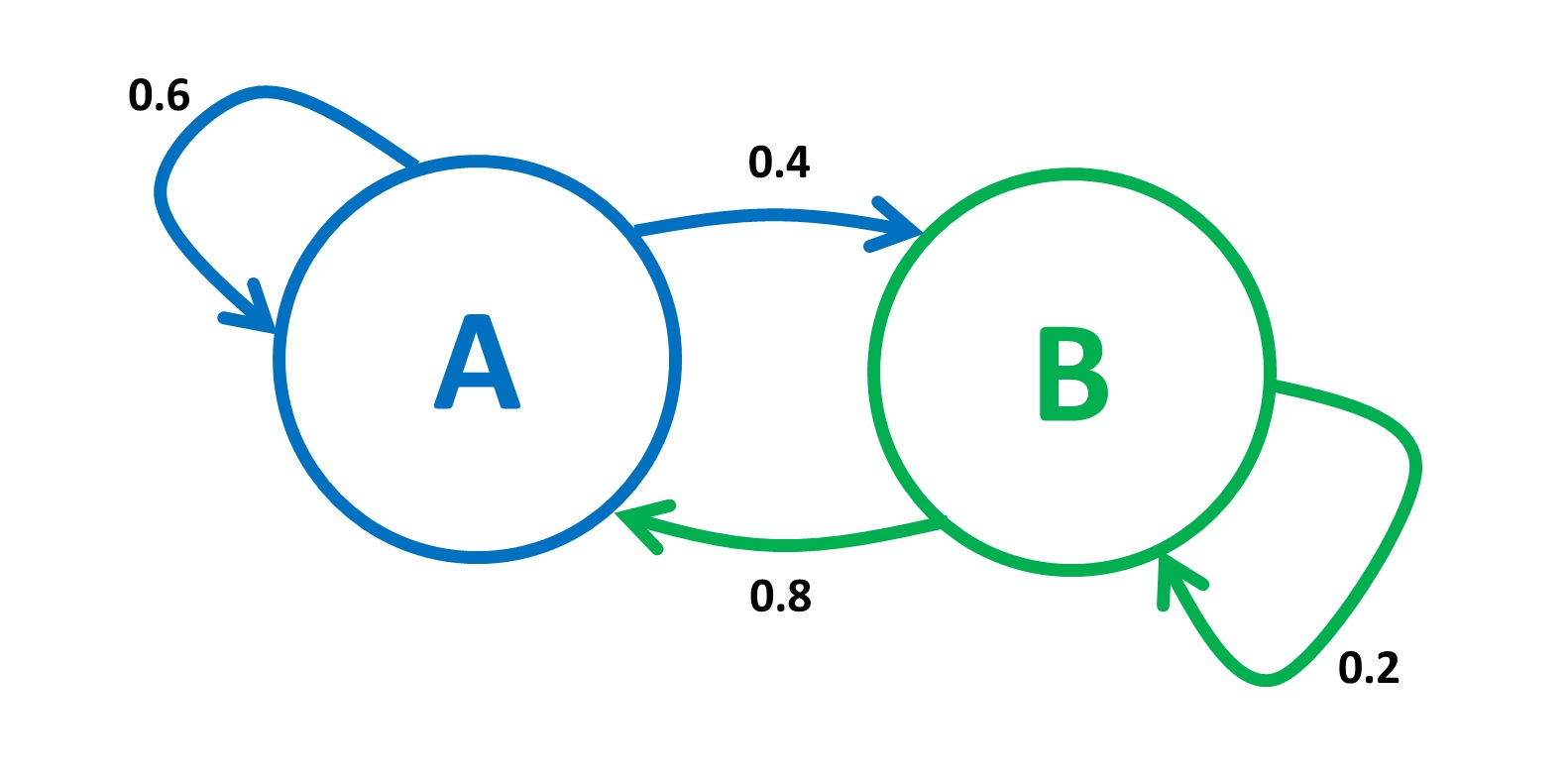
Эта вероятность может быть определена на основе исторических данных или при помощи искусственного интеллекта.

Матрица переходных вероятностей — это матрица, которая показывает вероятность перехода из одного состояния в другое. Каждый ряд матрицы соответствует текущему состоянию системы, а каждый столбец — очередному состоянию. Значения в матрице переходной вероятности показывают вероятность перехода из одного состояния в другое и служат основой для вычисления следующего состояния системы.

Пример такой матрицы:

| A | B | C |
------------------
A | 0 | 0.6 | 0.4 |
------------------
B | 0.4 | 0 | 0.6 |
------------------
C | 0.3 | 0.7 | 0 |


Эта матрица показывает, что вероятность перехода из состояния A в состояние B равна 0.6, из состояния A в состояние C — 0.4, из состояния B в состояние A — 0.4, из состояния B в состояние C — 0.6 и т.д. Здесь важно, чтобы сумма вероятностей перехода из каждого состояния во все возможные состояния была равна 1.

Марковская цепь — это процесс, в котором вероятность перехода из одного состояния в другое зависит только от текущего состояния. Это позволяет моделировать системы, где состояние в любой момент времени зависит только от предыдущего состояния, а не от всей предыдущей истории вычислений.

Основные свойства марковских цепей

Свойство Маркова — это ключевое свойство Марковской цепи. Оно гласит, что вероятность перехода из одного состояния в другое зависит только от текущего состояния, а не от предыдущих состояний. Это означает, что прошлое не имеет влияния на будущее, и вероятности являются фиксированными для каждого текущего состояния. Благодаря этому свойству Марковские цепи часто используются для моделирования процессов, которые могут быть описаны как последовательность случайных событий.

Свойство эргодичности — это важное свойство Марковских цепей. Оно означает, что в такой цепи существует единственное стационарное распределение и любое начальное распределение сходится к этому стационарному распределению.

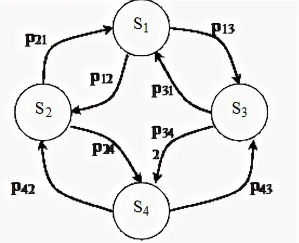
Это означает, что если мы начнем с какого-то определенного состояния, в конечном итоге мы будем приходить к определенному равновесному состоянию.

Третье свойство Марковских цепей — свойство полного перехода — означает, что из каждого состояния можно достичь любого другого состояния за конечное число шагов. Это свойство необходимо для того, чтобы убедиться в том, что модель может предсказывать переходы между всеми состояниями, что является необходимым условием для точного моделирования процесса.

Реализация Марковской цепи в Python

Пример №1.

У нас есть город, где может быть четыре состояния погоды: ясно, облачно, дождь и гроза. Состояние погоды на завтра зависит только от текущего состояния.

Если сегодня было «ясно», то завтра с вероятностью 0,6 будет «ясно», с вероятностью 0,2 будет «облачно», с вероятностью 0,1 — «дождь», и с вероятностью 0,1 — «гроза».

Если сегодня было «облачно», то завтра с вероятностью 0,1 будет «ясно», с вероятностью 0,5 будет «облачно», с вероятностью 0,2 — «дождь», и с вероятностью 0,2 — «гроза».

Если сегодня был «дождь», то завтра с вероятностью 0,3 будет «ясно», с вероятностью 0,3 будет «облачно», с вероятностью 0,2 — «дождь», и с вероятностью 0,2 — «гроза».

Если сегодня была «гроза», то завтра с вероятностью 0,4 будет «ясно», с вероятностью 0,3 будет «облачно», с вероятностью 0,1 — «дождь», и с вероятностью 0,2 — «гроза».

Мы хотим предсказать состояние погоды на завтра, опираясь на текущую погоду.

Реализуем код:

import numpy as np #numpy - мощнейшая библиотека для реализации Марковской цепи

# задаем вероятности переходов
transition_probabilities = [
    [0.6, 0.2, 0.1, 0.1],  # из "ясно"
    [0.1, 0.5, 0.2, 0.2],  # из "облачно"
    [0.3, 0.3, 0.2, 0.2],  # из "дождь"
    [0.4, 0.3, 0.1, 0.2],  # из "гроза"
]

# создаем массив состояний
states = ["ясно", "облачно", "дождь", "гроза"]

def predict_weather(today, days=1):
    # находим текущее состояние погоды
    current_state = states.index(today)
    
    # создаем вектор начальных вероятностей
    current_probabilities = np.zeros(len(states))
    current_probabilities[current_state] = 1
    
    # прогнозируем погоду на несколько дней
    for i in range(days):
        current_probabilities = np.dot(current_probabilities, transition_probabilities)
        
    # найдем индекс максимального элемента вектора вероятностей - это и будет предсказанное состояние погоды
    predicted_state_index = np.argmax(current_probabilities)
    
    # вернем предсказанное состояние погоды
    return states[predicted_state_index]
    
# пример использования функции - предсказание погоды на завтра, если сегодня "ясно"
print(predict_weather("ясно")) # результат: "ясно"

В этом коде мы определяем матрицу вероятностей переходов (transitionprobabilities) и массив состояний (states).

Функция predictweather() принимает в качестве аргументов текущее состояние погоды today и количество дней days, на которые нужно прогнозировать погоду. Функция возвращает предсказанное состояние погоды на days дней вперед от today.

Алгоритм работы функции заключается в следующем:

1. Определяем текущее состояние погоды (currentstate) на основе значения today.

2. Создаем вектор начальных вероятностей (currentprobabilities), в котором значение 1 на месте текущего состояния, а остальные элементы равны 0.

3. Производим умножение currentprobabilities на матрицу transitionprobabilities столько раз, сколько указано в days. Результат этого умножения будет являться вектором вероятностей для days дней вперед.

4. Находим индекс максимального элемента полученного вектора вероятностей и возвращаем соответствующее значение из массива состояний — это и будет предсказанное состояние погоды.

Пример №2

Предположим, что мы проводим эксперимент с монеткой, которая может выпасть на орла или решку. При каждом броске монетки мы записываем результат броска (0 — орёл, 1 — решка) и переходим к следующему броску. Мы хотим создать марковскую цепь, которая будет предсказывать вероятность выпадения орла или решки в следующем броске, в зависимости от количества орлов и решек в прошлых бросках.

Сначала создадим список всех возможных состояний марковской цепи. Каждое состояние будет представлять собой строку из двух символов, где первый символ обозначает количество орлов, а второй символ — количество решек в прошлых бросках. Таким образом, список состояний будет выглядеть следующим образом:

states = ['00', '01', '10', '11']

Теперь нужно создать матрицу переходных вероятностей. Матрица будет иметь размерность 4x4 (так как у нас 4 состояния), где каждый элемент матрицы будет представлять собой вероятность перехода из одного состояния в другое. Для простоты будем считать, что вероятность выпадения орла или решки на каждом броске равна 0.5.

transition_matrix = [
    [0.5, 0.5, 0, 0],
    [0, 0, 0.5, 0.5],
    [0.5, 0.5, 0, 0],
    [0, 0, 0.5, 0.5]
]

Элемент transition_matrix[0][1] обозначает вероятность перехода из состояния '00' (0 орлов и 0 решек) в состояние '01' (0 орлов и 1 решка) и равен 0.5.

Осталось только написать функцию для нахождения вероятности выпадения орла или решки в следующем броске, в зависимости от состояния в текущем броске и матрицы переходных вероятностей.

import numpy as np

def predict_next_state(current_state, transition_matrix):
    # Находим индекс текущего состояния в списке состояний
    current_index = states.index(current_state)
    # Вычисляем вероятности перехода из текущего состояния в каждое другое состояние
    probabilities = transition_matrix[current_index]
    # Выбираем только те вероятности, которые соответствуют выбранному символу (0 - орел, 1 - решка)
    next_probabilities = []
    for i in range(len(states)):
        if states[i][0] == current_state[0]:
            next_probabilities.append(probabilities[i])
    # Нормируем вероятности и выбираем наивысшую
    next_probabilities = np.array(next_probabilities)
    next_probabilities /= sum(next_probabilities)
    # Выбираем наивысшую вероятность и возвращаем соответствующий символ (0 - орел, 1 - решка)
    if np.random.choice([0, 1], p=next_probabilities) == 0:
        return '0'
    else:
        return '1'

Например, вызов функции predict_next_state('01', transition_matrix) может вернуть символ '0' с вероятностью 0.5 или символ '1' с вероятностью 0.5, что соответствует вероятностям перехода из состояния '01' в состояния '00' и '01' в соответствующей матрице переходных вероятностей.

Все эти примеры — довольно просты, но в общем и целом объясняют работу Марковских цепей. Я предлагаю вам решить следующую задачу самостоятельно:
Необходимо разработать модель поведения оленей на территории национального парка с использованием марковских цепей, учитывая различные факторы, такие как сезон, погода, наличие хищников и прочее. На основе данной модели сотрудники национального парка могут предпринимать меры по улучшению условий для жизни оленей и сохранения их популяции.

Ограничения и проблемы

У Марковской модели есть свои ограничения и проблемы, которые могут ограничить их применимость.

Ограниченность построения моделей:
Одним из ограничений Марковских цепей является ограниченность возможности построения моделей. Это связано с тем, что, хотя эти модели могут быть очень полезными, но все же не могут описывать каждый процесс во всех деталях. Кроме того, эти модели основаны на предположении о стационарности, то есть что вероятности переходов между состояниями не меняются со временем и не зависят от начального состояния системы.

Границы применимости и стабильность результатов:
Другой проблемой Марковских цепей является граница их применимости. Не все случайные процессы можно моделировать Марковскими цепями, поскольку некоторые процессы могут иметь более сложную структуру зависимостей между событиями. Кроме того, результаты моделирования могут быть неустойчивыми, если вероятности переходов между состояниями отличаются для разных начальных состояний.

Неудачные прогнозы и ошибки:
В некоторых случаях Марковские цепи могут приводить к неудачным прогнозам и ошибкам. Например, если вероятность перехода между состояниями слишком высока или низкая, то это может привести к неправильным прогнозам. Кроме того, если не учитывать все возможные состояния, то может возникнуть ложная уверенность в правильности результатов.

Таким образом, марковские цепи представляют собой мощный инструмент для моделирования различных процессов, особенно связанных с вероятностным поведением. Они широко используются в различных областях, включая экономику, физику, биологию и технические науки. Марковские цепи стали неотъемлемой частью современной статистики и машинного обучения, а также нашли свое применение в анализе данных, разработке программного обеспечения и в других областях, где требуется моделирование вероятностных процессов.

В качестве заключения хочу порекомендовать бесплатный вебинар от OTUS, в рамках которого будут рассмотрены описание, характерные свойства и характеристики разных архитектурных моделей. Зарегистрироваться на вебинар можно по этой ссылке.