Привет, Хаброжители!

«Python для хакеров. Нетривиальные проекты и задачи» делает упор на реальные проекты, так что от экспериментирования с синтаксисом вы сразу перейдете к написанию полноценных программ. Развивая свои навыки разработки на Python, вы будете проводить научные опыты, изучать статистику и решать задачи, которые не давали покоя гениям на протяжении многих лет, и даже займетесь обнаружением далеких экзопланет.

Каждая глава начинается с четко поставленной цели и обсуждения способов решения задачи. Далее следует собственно миссия и стратегия действий, построенная таким образом, чтобы вы научились мыслить как программист. Вы будете руководить спасательной операцией береговой охраны, спланируете и осуществите полет космического корабля на Луну, реализуете ограничение доступа в секретную лабораторию с помощью распознавания лиц и не только это.

Программы, представленные в книге, не отпугнут даже новичков. Вы будете осваивать все более сложные техники и наращивать навыки написания кода. Справившись со всеми миссиями, вы будете готовы к самостоятельному решению любых сложных реальных задач с помощью Python.

Проект #10. Выбор посадочных мест на Марсе

Представьте, что в качестве интерна вы работаете в NASA над проектом «Орфей». Этот проект посвящен прослушиванию марсотрясений и изучению внутренней структуры планеты, наподобие миссии InSight 2018 года. Поскольку цель «Орфея» — изучение внутреннего строения Марса, то интересные элементы поверхности планеты особой роли не играют. В первую очередь важна безопасность, что делает этот проект мечтой любого инженера.

Наша задача — найти не менее десятка прямоугольных областей, из которых специалисты NASA смогут отобрать варианты посадочных площадок в форме эллипса. Ваш наставник поясняет, что искомые области должны представлять прямоугольники длиной 670 км (В–З) и шириной 335 км (С–Ю). Исходя из требований безопасности, эти локации должны располагаться по обе стороны экватора между 30° северной и 30° южной широты, находиться в низинной части и быть максимально ровными и плоскими.

ЗАДАЧА

Написать программу Python, которая использует карту MOLA для выбора 20 наиболее безопасных областей площадью 670 х 335 км возле марсианского экватора, из которых можно будет отобрать посадочные площадки эллиптической формы для модуля «Орфей».

Стратегия

Сначала нам надо найти способ разделить цифровую карту MOLA на прямоугольные области и собрать статистические данные о том, на какой высоте они располагаются и насколько ровная их поверхность. Это означает, что мы будем работать с пикселями, поэтому потребуются инструменты для обработки изображений. А поскольку NASA всегда стремится к экономии, то и использовать придется бесплатные открытые библиотеки, такие как OpenCV, Python Imaging Library (PIL), tkinter и NumPy. Обзор и инструкции об установке OpenCV и NumPy ищите в разделе «Установка библиотек Python» на с. 31, а о PIL — в разделе «Модули Word Cloud и PIL» на с. 102. Что же касается tkinter, то этот модуль изначально включен в Python.

Чтобы учесть перепад уровня высот для каждой области, можно просто вычислить среднюю высоту. Для измерения степени пересеченности поверхности в заданном масштабе можно использовать разные варианты, в том числе весьма замысловатые. Помимо определения того, насколько поверхность ровная, на основе данных о высоте, можно поискать дифференциальное затенение на стереоизображениях; количество рассеивания в радиолокационных, лазерных и микроволновых отражениях; термические вариации в инфракрасных изображениях и т. д. Многие оценки основаны на утомительном анализе местности вдоль трансектов. Трансекты — это линии, нарисованные на поверхности планеты, вдоль которых измеряют и тщательно исследуют перепады высот. Ну а поскольку вы все же не интерн, которого взяли на лето и которого интересует лишь как поскорее освободиться от трехмесячной практики, то вам нужно хорошо решить задачу. Постараемся все упростить — для этого используем два типичных измерения, которые применимы к каждой прямоугольной области: стандартное отклонение и значение перепада высот.

Стандартное отклонение (standard deviation, StD), также называемое физиками среднеквадратическим, представляет меру распространения множества чисел. Низкое стандартное отклонение указывает, что значения во множестве близки к среднему. Высокое же свидетельствует о том, что они распределены по более обширному диапазону. Область карты с низким стандартным отклонением высоты означает, что эта область плоская с перепадами, немного отличающимися от среднего значения высоты.

Технически стандартное отклонение для набора образцов — это квадратный корень из усредненного квадрата отклонений от среднего значения. Представляется же оно следующей формулой:


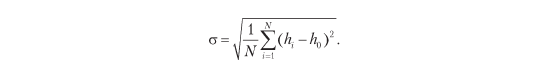
Здесь σ — это стандартное отклонение, N — количество образцов, h_i — текущий образец высоты, а h₀ — среднее по всем высотам.

Высота неровностей профиля (peak-to-valley, PV) — это разница в высоте между самой высокой и самой низкой точками поверхности, то есть максимальное изменение высоты поверхности. Это важный показатель, так как поверхность может обладать относительно низким, предполагающим ровную поверхность, стандартным отклонением, но при этом быть небезопасной, как показано на рис. 7.3.


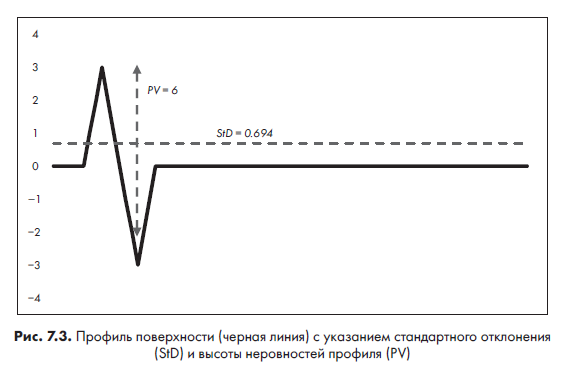
Показатели стандартного отклонения и высоты неровностей профиля можно использовать в качестве сравнительных метрик. Для каждой прямоугольной области мы ищем наименьшие значения каждой из этих метрик. А так как каждая запись несколько отличается, то мы отыщем 20 лучших областей для каждой из этих метрик, а затем выберем только те области, для которых метрики пересекаются. Это позволит найти наиболее удачные прямоугольные площадки.

Код для выбора мест посадки

В программе site_selector.py используются полутоновое изображение карты (рис. 7.4) для выбора прямоугольных посадочных областей и затененная цветная карта (см. рис. 7.2) для их отметки. На полутоновом изображении высота представлена одним каналом, поэтому его проще использовать, чем трехканальную RGB-картинку.


Программа, полутоновое изображение (mola_1024×501.png) и цветное изображение (mola_color_1024×506.png) находятся в каталоге Chapter_7, доступном для скачивания с nostarch.com/real-world-python. Разместите эти файлы в одном каталоге и не переименовывайте.

ПРИМЕЧАНИЕ

Карта MOLA доступна в различных размерах и разрешениях. Мы сейчас используем самую маленькую с целью сокращения времени скачивания и выполнения.

Импорт модулей и присваивание вводимых пользователем констант

Код листинга 7.1 импортирует модули и присваивает константы, представляющие вводимые пользователем параметры: имена изображений, размеры прямоугольных областей, максимальный порог высоты и количество предлагаемых к рассмотрению прямоугольников.

Листинг 7.1. Импорт модулей и присваивание вводимых пользователем констант

site_selector.py, часть 1
     import tkinter as tk
     from PIL import Image, ImageTk
     import numpy as np
     import cv2 as cv

     # Константы: пользовательский ввод:
     IMG_GRAY = cv.imread('mola_1024x501.png', cv.IMREAD_GRAYSCALE)
     IMG_COLOR = cv.imread('mola_color_1024x506.png')
     RECT_WIDTH_KM = 670
     RECT_HT_KM = 335
     MAX_ELEV_LIMIT = 55
     NUM_CANDIDATES = 20
     MARS_CIRCUM = 21344

Начинаем с импорта модуля tkinter. Это предустановленная в Python библиотека GUI для разработки десктопных приложений. С ее помощью мы будем создавать заключительное отображение: окно с цветной картой MOLA вверху и текстовым описанием отмеченных прямоугольников внизу. На большинстве машин с Windows, macOS и Linux tkinter уже установлен. Если у вас этой библиотеки нет или нужна последняя версия, то можно скачать и установить ее со страницы www.activestate.com. Онлайн-документация для этого модуля находится по адресу docs.python.org/3/library/tk.html.

Далее импортируем модули Image и ImageTK из Python Imaging Library. Image предоставляет класс, отображающий картинку PIL. Кроме того, он содержит функции, в том числе необходимые для загрузки изображений из файлов и создания новых изображений. Модуль ImageTK обеспечивает поддержку для создания и изменения объектов BitmapImage библиотеки tkinter из изображений PIL. Опять же, мы используем их в конце программы, чтобы разместить в итоговом окне цветную карту и описания. В завершение импортируем библиотеки NumPy и OpenCV.

Теперь присваиваем представляющие пользовательский ввод константы, которые по ходу выполнения программы изменяться не будут. Сначала с помощью метода OpenCV imread() скачиваем полутоновое изображение MOLA. Обратите внимание, что нужно использовать флаг cv.IMREAD_GRAYSCALE, поскольку этот метод по умолчанию скачивает изображения в цвете. Повторяем тот же код без флага, чтобы скачать уже цветной вариант. Затем добавляем константы для размера прямоугольников. В следующем листинге мы преобразуем эти размеры в пиксели для использования совместно с картой.

Теперь, чтобы наши прямоугольники гарантированно попали в низинные ровные области, нужно ограничить поиск плоскими участками с малым количеством кратеров. Считается, что эти области — дно древних океанов. Таким образом, необходимо установить верхний порог высоты до полутонового значения 55, которое примерно соответствует областям, считающимся древними береговыми линиями (рис. 7.5).


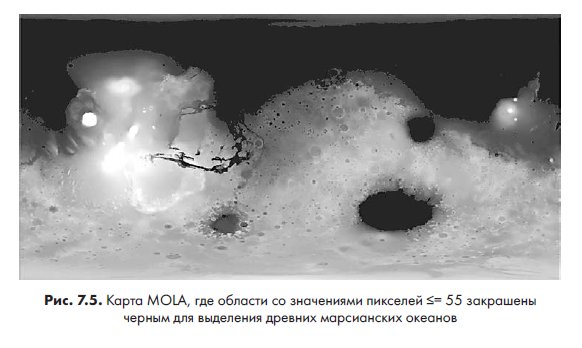
Теперь в переменной NUM_CANDIDATES указываем количество прямоугольников для отображения. Позднее мы выберем их из упорядоченного списка статистических данных о прямоугольниках. Завершаем код назначением константы, которая будет хранить протяженность окружности Марса в километрах. Ее мы используем позже для определения количества пикселей на километр.

Присваивание выводимых констант и создание объекта экрана

В листинге выполняется присваивание констант, выводимых из других констант. Эти значения будут обновляться автоматически при изменении пользователем предыдущих констант, например для тестирования размеров прямоугольников или границ высоты. Оканчивается этот листинг созданием tkinter-объектов screen и canvas для итогового отображения.

Листинг 7.2. Присваивание выводимых констант и настройка экрана tkinter

site_selector.py, part 2
     # Константы: выводимые:
     IMG_HT, IMG_WIDTH = IMG_GRAY.shape
     PIXELS_PER_KM = IMG_WIDTH / MARS_CIRCUM
     RECT_WIDTH = int(PIXELS_PER_KM * RECT_WIDTH_KM)
     RECT_HT = int(PIXELS_PER_KM * RECT_HT_KM)
❶    LAT_30_N = int(IMG_HT / 3)
     LAT_30_S = LAT_30_N * 2
     STEP_X = int(RECT_WIDTH / 2)
     STEP_Y = int(RECT_HT / 2)

❷    screen = tk.Tk()
     canvas = tk.Canvas(screen, width=IMG_WIDTH, height=IMG_HT + 130)

Распаковываем высоту и ширину изображения с помощью атрибута shape. OpenCV сохраняет изображения как nd-массивы NumPy, являющиеся n-мерными массивами или таблицами элементов одного типа. Для массива изображений shape является кортежем из количества рядов, столбцов и каналов. Высота представляет количество пиксельных строк в изображении, а ширина — количество пиксельных столбцов. Каналы представляют число элементов, используемых для выражения каждого пикселя (например, красный, зеленый и синий). Для полутоновых изображений с одним каналом shape является просто кортежем из высоты и ширины области.

Чтобы преобразовать измерение прямоугольных областей из километров в пиксели, нужно знать, сколько пикселей в каждом километре. Поэтому мы делим ширину изображения на длину окружности, получая тем самым соотношение пикселей на километр в области экватора. Затем преобразуем ширину и высоту в пиксели. Эти результаты понадобятся, чтобы вывести значения для квантования индекса, поэтому необходимо, чтобы они были целыми числами, для чего используется int(). Значение этих констант теперь должно быть 32 и 16 соответственно.

Нам нужно ограничить поиск наиболее теплыми и солнечными участками, которые располагаются с двух сторон от экватора — между 30° северной и 30° южной широты (рис. 7.6). Можно сказать, что этот регион соответствует земным тропикам.


Значения широты начинаются от 0° у экватора и заканчиваются на 90° у полюсов. Чтобы найти 30° северной широты, нужно просто разделить высоту изображения на 3 ❶. Чтобы получить 30° для южной широты, нужно удвоить число пикселей, которое потребовалось для нахождения предыдущего значения для севера.

Ограничение поиска экваториальным регионом имеет положительный побочный эффект. Используемая карта MOLA основана на цилиндрической проекции, применяемой для отображения карты с глобуса на плоскость. В результате такого переноса сходящиеся линии долготы становятся параллельными, что сильно искажает детали в районе полюсов. Вы могли заметить это по настенным картам Земли, где Гренландия выглядит как континент, а Антарктида невероятно огромная (рис. 7.7).


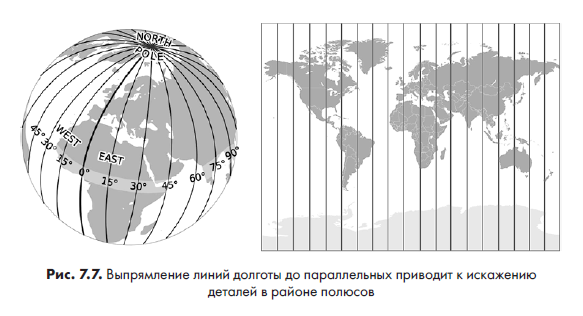
К счастью, в области экватора это искажение минимизируется, и уже не нужно учитывать его в размерах прямоугольников. Убедиться в этом можно, проверив форму кратеров на карте MOLA. До тех пор пока они остаются аккуратными и круглыми (а не овальными), вызываемые проекцией эффекты можно игнорировать.

Далее нужно поделить карту на прямоугольные области. Логично начать с верхнего левого угла, расположенного под линией 30° северной широты (рис. 7.8).


Программа нарисует этот прямоугольник, пронумерует его и вычислит внутреннюю статистику высот. Затем она сместит прямоугольник на восток и повторит процесс. Расстояние каждого очередного смещения определяется константами STEP_X и STEP_Y и зависит от так называемого алиасинга.

Алиасинг — это проблема разрешения. Он возникает, когда берется недостаточное количество образцов для определения всех важных деталей поверхности в некой области. Это может привести к тому, что мы «пропустим» такую деталь, как кратер, и не сможем его распознать. К примеру, на рис. 7.9А между двумя кратерами наблюдается подходящий гладкий посадочный эллипс. Однако, как мы видим, на рис. 7.9В этому эллипсу не соответствует ни одна прямоугольная область. Оба соседних прямоугольника частично включают края кратеров. В результате ни одна из очерченных ими областей не содержит подходящего посадочного эллипса, несмотря на то что в их смежной области он есть.

При таком порядке расположения прямоугольников эллипс на рис. 7.9А попадает под эффект алиасинга. Если же сместить каждый прямоугольник на половину его ширины, как на рис. 7.9С, то эта ровная область будет правильно отобрана и распознана.


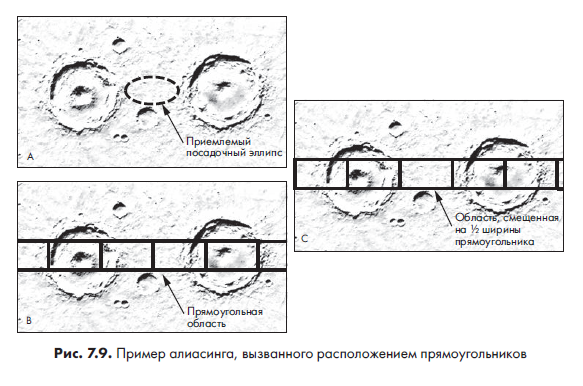
Общим правилом для предотвращения эффектов алиасинга является определение шага меньше или равным половине ширины наименьшей детали, которую требуется определить. Для данного проекта мы используем половину ширины прямоугольника, чтобы не усложнять процесс отображения.

Теперь пора заглянуть вперед и разобрать заключительный вариант карты. Создаем экземпляр screen класса Tk() модуля tkinter ❷. Приложение tkinter является оболочкой Python для набора инструментов GUI под названием Tk, изначально написанным на языке TCL. Окно screen ему требуется для связи с внутренним интерпретатором tcl/tk, который переводит команды tkinter в команды tcl/tk.

Далее создаем tkinter-объект canvas. Это область для рисования прямоугольников, спроектированная для сложных графических макетов, текста, виджетов и фреймов. Передаем ей объект screen, устанавливаем ее ширину равной изображению MOLA, а высоту — равной изображению MOLA плюс 130. В дополнительной области под картинкой мы поместим текст с обобщающей статистикой отображаемых прямоугольников.

Обычно только что описанный код tkinter помещается в конце программ, а не в начале. Я же решил разместить его вверху, чтобы упростить восприятие сопутствующих пояснений. Также можно встроить его в функцию, выполняющую финальное отображение. Однако это может вызвать проблемы у пользователей macOS. Для версии macOS 10.6 или более поздних предоставляемый Apple набор инструментов Tcl/Tk 8.5 имеет серьезные баги, которые могут вызвать падение приложения (подробнее — по ссылке www.python.org/download/mac/tcltk).

Определение и инициализация класса Search

В листинге 7.3 определяем класс, который мы используем для поиска подходящих прямоугольных областей. Следом идет определение метода инициализации _init_(), используемого для инстанцирования новых объектов. Чтобы вкратце узнать об ООП, обратитесь к разделу «Определение класса Search» на с. 36, где мы также определяли класс поиска.

Листинг 7.3. Определение класса Search и метода _init_()

site_selector.py, часть 3
     class Search():
          """Считывание изображения и определение посадочных прямоугольников
          на основе входных критериев"""

     def __init__(self, name):
          self.name = name
       ❶  self.rect_coords = {}
          self.rect_means = {}
          self.rect_ptps = {}
          self.rect_stds = {}
      ❷   self.ptp_filtered = []
          self.std_filtered = []
          self.high_graded_rects = []

Определяем класс Search. Далее прописываем метод _init_(), используемый для создания новых объектов. Параметр name позволит давать собственное имя каждому создаваемому в функции main() объекту.

Теперь можно присваивать атрибуты. Начинаем со связывания имени объекта с аргументами, которые будем предоставлять при его создании. Далее присваиваем пустые словари для хранения важных статистических данных для каждого прямоугольника (rect) ❶. К ним относятся координаты его угловых точек, средняя высота (mean elevation), высота неровностей профиля (peak-to-valley) и стандартное отклонение (standard deviation). В качестве ключа во всех словарях будут использоваться последовательные числа, начиная с 1. Эти данные нужно отфильтровать, чтобы найти наименьшие значения, поэтому создаем два пустых списка для их хранения ❷. Обратите внимание, что для представления статистики высоты неровностей профиля (peak-to-valley) я использую выражение ptp, а не ptv. Это необходимо для согласования со встроенным в NumPy методом peak-to-peak, занимающимся ее вычислением.

В конце программы мы поместим прямоугольники, которые одновременно встречаются в упорядоченных списках стандартного отклонения и высот неровностей профиля, в новый список high_graded_rects. Этот список будет содержать номера прямоугольников с наименьшими общими показателями. Эти прямоугольники окажутся лучшими местами для посадочных эллипсов.



Более подробно с книгой можно ознакомиться на сайте издательства:

» Оглавление
» Отрывок

По факту оплаты бумажной версии книги на e-mail высылается электронная книга.
Для Хаброжителей скидка 25% по купону — Python