
Нам очень повезло, что Земля вращается вокруг своей оси. Вращение создает центробежное ускорение, которое возрастает от полюсов к экватору.
Это наводит на мысли, что если измерить абсолютное ускорение свободного падения чувствительным акселерометром, то можно вычислить свою широту. Насколько реально сделать такой электронный прибор?
Из физики вращательного движения известно, что при вращении по окружности образуется центробежное ускорение. Его модуль определяется формулой (1)
Тут омега - это угловая скорость вращения Земли. T= 24 часа = 86400 секунд
из (1) и (2) получается (3)
схема вычислений
Угол между вектором центробежной силы и силой гравитации равен (2)
Для вычисления модуля вектора суммарного ускорения g можно прибегнуть к формуле модуля суммы векторов. Это можно сделать по теореме косинусов.

Квадрат модуля силы тяжести примем равным
именно результат формулы (6) покажет акселерометр
или
упростив получается формула (8). Предположим что R и T константы.
Получается вот такой график зависимости полного ускорения свободного падения от широты
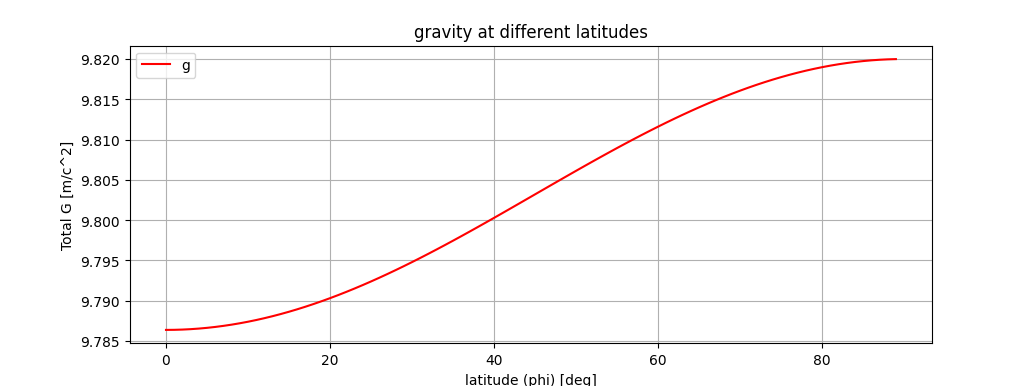
Эту формул (8) можно вообще даже не вычислять, а раcсчитать на фазе компиляции прошивки для каждого градуса и хранить Look Up таблицу в ROM памяти микроконтроллера (секция .rodata).
import math
import matplotlib.pyplot as plt
import numpy as np
T=86400 ;
Gg=9.82;
pi = math.pi
print(pi)
R=6356863
phi_deg = np.arange(0,90,1)
phi_rad=np.deg2rad(phi_deg)
r=R*np.cos(phi_rad)
omera = (2*pi/T)
a = r*(omera**2)
sqrt_arg = Gg**2 +(a**2) - 2*a*Gg*np.cos(2*pi-phi_rad)
g1 = np.sqrt(sqrt_arg)
#plt.axis([0,90,-0.1,10.1])
plt.title('gravity at different latitudes')
plt.grid(True)
plt.xlabel('latitude (phi) [deg]')
plt.ylabel('Total G [m/c^2]')
plt.plot(phi_deg,g1,'r')
#plt.plot(phi_deg,a,'b')
plt.legend(['g','a'], loc=2)
plt.show()
Задача определения широты сводится к тому, что надо научиться измерять ускорение свободного падания с точностью (9.82-9.78)/90.0 = 0.0004444444444444547 m/c^2. То есть интерес представляют четверные цифры после запятой! Где бы мы не ходили по Земле с акселерометром наши показания в теории будут отличаться только на +/-0.040 m/c^2
Существуют ли такие MEMS акселерометры, которые показывают ускорение с точностью 4 цифры после запятой?
Вот например реальный дешевый MEMS акселерометр LIS3DH за 300 RUR обладает максимальной чувствительностью +/- 0.001g = 0.00982 m/c^2 на разряд. Это значит, что акселерометром LIS3DH можно вычислить широту с точностью +/- 22 градуса. Маловато.
Вот обзор еще нескольких MEMS акселерометров
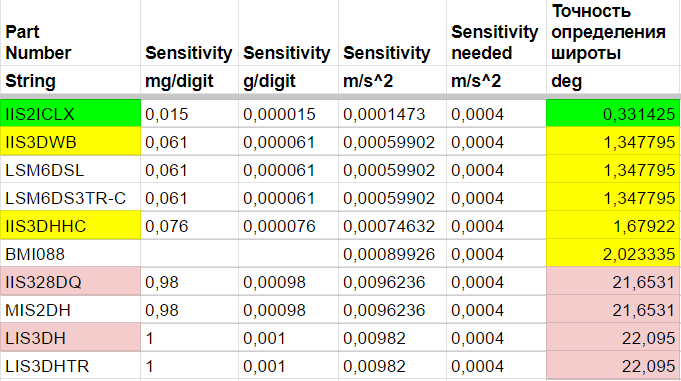
https://docs.google.com/spreadsheets/d/1fdQT1M2ptGPf8z9bGbsvIadOyoKVGr3zhjSLuwBl80s/edit#gid=0
Глядя на формулу (3) можно, кстати, заметить что, если бы Земля вращалась с периодом 1.4 часа, то на экваторе бы наступила невесомость. Это позволило бы пользоваться для определения широты простыми акселерометрами. Однако это бы вызвало на экваторе область пониженного давления, подули бы сильные ветры от полюсов к экватору и весь воздух от полюсов улетучился бы в космос через экватор и всем бы наступил конец.
К счастью Земля вращается достаточно медленно. Более того Земля еще и замедляется в своем вращении вокруг своей оси. Это вызвано тем, что Луна вызывает приливы и океаны тем самым тормозят Землю.
Поэтому эффектом неоднородности притяжения вдоль меридианов можно пользоваться пока не поздно.
Достоинства навигации по акселерометру:
++1 Измерение широты происходит мгновенно. Это если измерять g MEMS акселерометром.
Недостатки навигации по акселерометру:
--1 измерительный прибор должен быть статичным
--2 акселерометр должен быть точным и чувствительным.
--3 невозможно измерять координаты акселерометром в море из-за волн.
Стоит отметить что в этих расчетах не учитываются гравитационные аномалии. Не учитываются вклад абсолютной гравитационной составляющей, которая тоже зависит от широты из-за того, что Земля это не шар а эллипсоид сплюснутый на 20 км в полюсах.
Вывод
Чтобы говорить о измерении широты акселерометром надо акселерометр с точностью 4 цифры после запятой и такие акселерометры есть (IIS2ICLX).
Links
Online LaTeX Equation Editor - create, integrate and download
Комментарии (30)

dsoastro
29.06.2023 18:03+5Но ведь Земля не шар, думаю эффект ее не шарообразности может быть сравним с эффектом от вращения, что усложняет задачу

Kopilov
29.06.2023 18:03+1Калибровка, конечно, потребуется, но по части чувствительности геоидальность только помогает (на экваторе и ускорение есть, и от центра дальше)

Akina
29.06.2023 18:03+5Задача определения широты сводится к тому, что надо научиться измерять ускорение свободного падания с точностью (9.82-9.78)/90.0 = 0.0004444444444444547 m/c^2.
Для справки - именно на столько различается ускорение свободного падения на уровне поверхности земли и приблизительно в 150 метрах над ней. То есть грубо: поднялся на 60 этаж, а по мнению этого "акселерометра" сместился на градус к экватору.

MaxAkaAltmer
29.06.2023 18:03+1
Земля не точка, интеграл по объему нужен - гравитация сначала ростет по мере подъема.
Akina
29.06.2023 18:03+1гравитация сначала ростет по мере подъема
Это с какого такого перепугу? В процессе подъёма с поверхности Земли точка измерения удаляется от ЛЮБОЙ точки Земли, что приводит к СНИЖЕНИЮ силы тяготения. Небоскрёбами и горой на горизонте можно пренебречь.
Нет, если рассматривать подъём из километровой шахты - то да, эффект роста силы тяжести по мере подъёма на начальном этапе имеет место быть.

MaxAkaAltmer
29.06.2023 18:03+2Интеграл по объему возьмите. То что в горизонте у земли, тянет вас в стороны, когда поднимаетесь - результирующий вектор направленный вниз поначалу будет рости. Не поленитесь - посчитайте.
Ну или поднимитесь на небоскреб и прислушайтесь к сосудам в ногах - это вполне можно даже почувствовать.

trir
29.06.2023 18:03+4Не учитываются аномалии гравитационного поля https://upload.wikimedia.org/wikipedia/commons/1/14/Gravity_anomalies_on_Earth.jpg

Radisto
29.06.2023 18:03+1Пишут, что величина даже больших гравитационных аномалий в 12 меньше разницы между g экватора и полюса

Albert2009Zi
29.06.2023 18:03+1Акселерометром мерять координаты так-то уж очень не комильфо. Можно применить дусы и обвешать по трём плоскостям гироплтаформу, тогда сильно точнее будет. Но в любом случае не сравнится с сигналами от трех спутников, благо их уже на орбиту хорошо понавешали.

aamonster
29.06.2023 18:03+1Учитывая, что "земля имеет форму чемодана" (c) погрешность будет великовата. Ну и в любом случае долготы не хватает, так что даже если у вас есть достаточно точный акселерометр – пользы мало. Но как лабораторная работа для старшеклассников – было бы интересно. Особенно если после получения результата следующим шагом сравнить его с действительностью и всем классом обсудить причины отличий.
Можно, кстати, вторую лабу сделать по измерению угла наклона магнитных силовых линий к земной поверхности. Тут ещё несколько любопытных нюансов всплывёт – разница между магнитными и географическими полюсами, магнитные аномалии.

MaxAkaAltmer
29.06.2023 18:03+3Нельзя полагаться на эти расчеты - например гравитация зависит от высоты, при чем нелинейно, стачала растет, потом падает. И еще куча моментов имеется.

simenoff
29.06.2023 18:03+1Почему сначала растёт? 0_o

MaxAkaAltmer
29.06.2023 18:03+1Потому что сила тяжести определяется векторной суммой гравитационного взаимодействия всех частичек, т.е. нужно брать интеграл по объему планеты относительно положения объекта.

simenoff
29.06.2023 18:03+1Где-нибудь можно об этом почитать?

MaxAkaAltmer
29.06.2023 18:03+1О том как взять интеграл?

MaxAkaAltmer
29.06.2023 18:03+1#include <iostream> #include <math.h> using namespace std; __inline double h_triangle_equ(double a, double r) { return sqrt(r*r-a*a/4.0); } __inline double h_triangle(double a, double b, double c) { double p = (a+b+c)/2.0; double rv = 2.0*sqrt(p*(p-a)*(p-b)*(p-c))/a; return rv; } void sh_numeric_integral() { const int alt_parts = 1000; const double R = 6371000.0; const double alt_delta = R/double(alt_parts); const int lat_parts = 500; const double lat_delta = acos(-1.0)/double(lat_parts); const int lon_parts = lat_parts*2; const double lon_delta = (2.0*acos(-1.0))/double(lon_parts); const double density_start = 13500; const double density_end = 3000; const double m = 1; const double y = R+0; const double x = 0.0; const double z = 0.0; double v_test = 0.0, m_planet = 0.0; double gravity_x = 0.0, gravity_y = 0.0, gravity_z = 0.0; for(int alt = 0; alt< alt_parts; alt++ ) { double r_curr = double(alt+1)*alt_delta; double r_prev = double(alt)*alt_delta; double r_middle = double(alt+0.5)*alt_delta; double c = 2.0* r_curr * sin(lat_delta/2.0); double c_prev = 2.0* r_prev * sin(lat_delta/2.0); double density_curr = density_start+double(alt+0.5)*((density_end-density_start)/double(alt_parts)); for(int lat = 0; lat<lat_parts; lat++ ) { double lat_start = lat*lat_delta-acos(-1.0)/2.0; double lat_middle = lat_start+lat_delta*0.5; double lat_end = lat_start+lat_delta; double a = abs(2.0*r_curr*cos(lat_start)*sin(lon_delta/2.0)); double b = abs(2.0*r_curr*cos(lat_end)*sin(lon_delta/2.0)); double H = sqrt(c*c-((b-a)/2.0)*((b-a)/2.0)); double s_curr = ((a+b)/2.0)*H; double h_curr = h_triangle(H,h_triangle_equ(a,r_curr),h_triangle_equ(b,r_curr)); double a_prev = abs(2.0*r_prev*cos(lat_start)*sin(lon_delta/2.0)); double b_prev = abs(2.0*r_prev*cos(lat_end)*sin(lon_delta/2.0)); double H_prev = sqrt(c_prev*c_prev-((b_prev-a_prev)/2.0)*((b_prev-a_prev)/2.0)); double s_prev = ((a_prev+b_prev)/2.0)*H_prev; double h_prev = alt ? h_triangle(H_prev,h_triangle_equ(a_prev,r_prev),h_triangle_equ(b_prev,r_prev)) : 0.0; for(int lon = 0; lon<lon_parts; lon++ ) { double lon_middle = double(lon+0.5)*lon_delta-acos(-1.0); double cm_x = r_middle*cos(lat_middle)*sin(lon_middle); double cm_y = r_middle*sin(lat_middle); double cm_z = r_middle*cos(lat_middle)*cos(lon_middle); double distp2 = ((cm_x-x)*(cm_x-x)+(cm_y-y)*(cm_y-y)+(cm_z-z)*(cm_z-z)); double dist = sqrt(distp2); double dv = (s_curr * h_curr)/3.0 - (s_prev * h_prev)/3.0; double M = dv*density_curr; double f = (m*M*0.0000000000667)/distp2; gravity_x += (cm_x-x)*f/dist; gravity_y += (cm_y-y)*f/dist; gravity_z += (cm_z-z)*f/dist; v_test += dv; m_planet += M; } } } double result_gravity = sqrt(gravity_x*gravity_x+gravity_y*gravity_y+gravity_z*gravity_z); double v_test_formula = (4.0*acos(-1)*R*R*R)/3.0; cout << "Volume test: numeric = " << v_test << ", formula = " << v_test_formula << endl; cout << "Planet mass: " << m_planet << endl; cout << "Gravity: " << result_gravity << endl; } int main() { sh_numeric_integral(); return 0; }Каюсь - был неправ, видимо мои наблюдения были обусловлены локальными особенностями и я сделал неверные выводы, сейчас написал программу и проверил - с учетом перемены плотности вещества гравитация начинает уменьшаться ниже отметки в три тысячи километров под землей и от нее вверх довольно стабильна и лишь немного падает.

MaxAkaAltmer
29.06.2023 18:03+1Довольно похоже на Землю вышло =)
Volume test: numeric = 1.0831e+21, formula = 1.08321e+21
Planet mass: 6.09242e+24
Gravity: 9.97903

ferosod
29.06.2023 18:03+1Интересно было бы сравнить с точностью определения широты по углу наклона магнитных линий Земли к поверхности

Radisto
29.06.2023 18:03+1Это был бы интересный опыт. Правда, для него желательно попутешествовать в меридианальном направлении, а это дороговато))) и интересно было бы узнать, насколько действительно влияют приливы и отливы. Время прилива и отлива (гравитационное, конечно, не волна воды, которая смещена и определяется еще р рельефом дна и глубиной) само по себе может дать координату (долготу, скорее всего, для широты мне кажется сомнительно, абсолютные значения ускорения мало меняются. Хотя вектор может сильнее? Сравнивать по осям?), если конечно способ позволит относительно точно определить момент прохода "под луной". Правда, для этого надо прибор оставить в покое как минимум на сутки.

Radisto
29.06.2023 18:03+1Посмотрел тут в разных местах. Кажется, для этого нужна будет точность еще на порядки выше.

freeExec
29.06.2023 18:03+1Так давно в GNSS применяется
Ocean Loading BLQ Format
Нашёл первый попавшийся пример
Hidden text
An example of the output for station Onsala in BLQ-format $$ Ocean loading displacement $$ $$ Calculated using olfg/olmpp of H.-G. Scherneck $$ $$ COLUMN ORDER: M2 S2 N2 K2 K1 O1 P1 Q1 MF MM SSA $$ $$ ROW ORDER: $$ AMPLITUDES (m) $$ RADIAL $$ TANGENTL EW $$ TANGENTL NS $$ PHASES (degrees) $$ RADIAL $$ TANGENTL EW $$ TANGENTL NS $$ $$ Displacement is defined positive in upwards, South and West direction. $$ The phase lag is relative to Greenwich and lags positive. The $$ Gutenberg-Bullen Green's function is used. In the ocean tide model the $$ deficit of tidal water mass has been corrected by subtracting a uniform $$ layer of water with a certain phase lag globally. $$ $$ $$ Complete <model name> : No interpolation of ocean model was necessary $$ <model name>_PP : Ocean model has near the station been interpolated $$ $$ Ocean tide model: GOT00.2, long period tides from FES99 $$ $$ Onsala $$ GOT00.2_PP ID: Aug 16, 2001 13:35 $$ Computed by OLMPP by H G Scherneck, Onsala Space Observatory, 2001 $$ Onsala, RADI TANG lon/lat: 11.9264 57.3958 .00366 .00123 .00089 .00032 .00223 .00115 .00071 .00009 .00091 .00048 .00042 .00149 .00035 .00040 .00009 .00046 .00043 .00015 .00009 .00013 .00006 .00007 .00069 .00027 .00020 .00004 .00029 .00014 .00009 .00004 .00003 .00002 .00001 -62.3 -51.3 -94.8 -39.7 -57.7 -110.6 -60.3 -164.6 9.9 5.8 2.1 87.0 114.0 57.2 126.4 102.3 35.4 97.0 -6.8 -166.3 -169.8 -177.7 109.9 152.4 86.4 149.1 50.7 -59.4 47.7 173.6 -27.8 -1.5 7.3

Avante_sb
29.06.2023 18:03+1Учитываю зависимость изменения g от высоты над уровнем моря - способ пригоден только для моря, но в море волны. Кажется если сделать какой то "стэдикам" для акселерометра то в море вполне можно пользоваться и точность будет соизмерима со старыми способами определения широты. То есть не очень точно, но независимо от хронометра и облачности.

tormozedison
29.06.2023 18:03+1"невозможно измерять координаты акселерометром в море из-за волн"
Вообще на любом движущемся объекте, поскольку он хотя бы слегка, но трясётся.


Jury_78
Как повлияют Лунные и Солнечные приливы? Не точнее ли будет по компасу и часам?
p.s. Если нужна точность то лучше это - гравиметр.