Автор статьи: Артем Михайлов

В наши дни большое количество задач требует нахождение всех возможных комбинаций в наборе данных. Подобные ситуации могут возникнуть в различных областях, начиная от программирования и машинного обучения до игровой индустрии и задач комбинаторики. В таких случаях использование алгоритма backtracking — метода рекурсивного перебора всех возможных вариантов — может быть наиболее эффективным подходом.

Алгоритм backtracking (возврат к исходным данным) — это метод решения задачи перебора всех возможных вариантов с последующим выбором оптимального решения. Данный подход широко применяется в области разработки программного обеспечения, особенно в решении задач комбинаторной оптимизации, где требуется найти наилучшее решение из множества возможных комбинаций.

Принцип работы алгоритма backtracking основывается на рекурсивном итеративном процессе, который проходит по всем возможным ветвям решения задачи. Основной идеей является перебор всех возможных решений путем последовательного выбора вариантов и проверки их на соответствие заданным условиям.

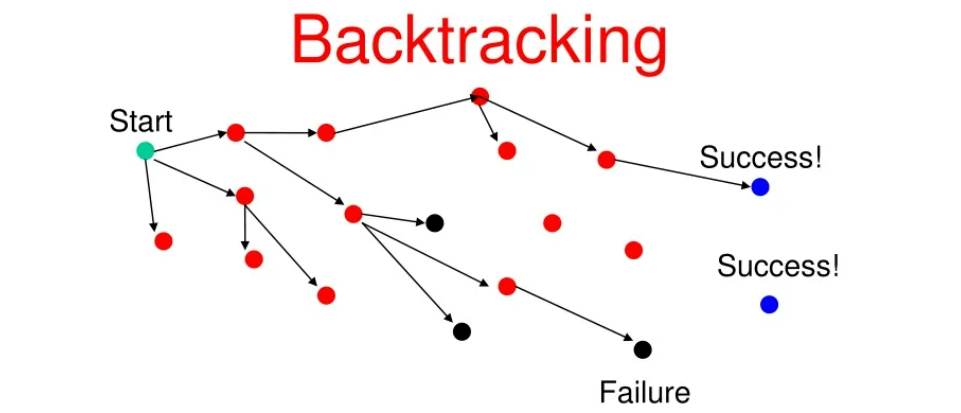
Процесс работы алгоритма начинается с инициализации начальных значений и установки начального состояния. Затем алгоритм приступает к выбору следующего возможного варианта решения и проверяет его на соответствие заданным ограничениям и условиям. Если вариант удовлетворяет условиям, то происходит переход в следующее состояние и продолжение процесса рекурсивно. В противном случае, если вариант не удовлетворяет условиям, алгоритм возвращает предыдущее состояние и продолжает выбор следующего варианта.

Процесс рекурсии продолжается до тех пор, пока не будут проверены все возможные варианты решения или найдено оптимальное решение. Важным аспектом работы алгоритма backtracking является проверка условий остановки, которые определяют момент, когда алгоритм должен завершить свою работу. Это может быть достижение определенной цели, исчерпание всех возможных вариантов или превышение временного лимита.

Одним из наиболее известных применений алгоритма backtracking является задача о расстановке ферзей на шахматной доске так, чтобы они не били друг друга. Другие примеры включают задачи о путешествии волновго алгоритма, о поиске пути в графе и о комбинаторной оптимизации.

Описание алгоритма backtracking

Первым шагом в алгоритме backtracking является выбор, который заключается в выборе подходящего элемента или состояния, чтобы продолжить решение задачи. Этот шаг определяет потенциальные варианты на следующем этапе алгоритма. Например, при решении задачи комбинаторной оптимизации выбор может быть связан с выбором элемента из заданного множества.

После выбора происходит проверка, где текущий выбранный элемент или состояние проверяется на соответствие критериям или ограничениям задачи. Если проверка проходит успешно, то мы переходим к следующему шагу. В противном случае, если элемент не подходит, алгоритм возвращает его, чтобы выбрать другой элемент и повторить проверку. Это позволяет нам избежать потенциально бесконечного цикла, и перемещает нас к следующему возможному варианту.

Третий шаг — откат, представляет собой возврат к предыдущему выбору и проверке, когда все возможные варианты были исчерпаны. Откат может произойти в случаях, когда текущий выбор не приводит к решению задачи или к моменту, когда мы исчерпали все возможные варианты. Когда откат происходит, мы отменяем текущий выбор и возвращаемся к предыдущему состоянию алгоритма, чтобы попробовать другой путь.

Четвертый шаг происходит после успешной проверки и выбора. На этом шаге мы продолжаем алгоритм, используя текущий выбор и двигаясь вперед к нахождению следующего возможного варианта или решения задачи. Этот шаг может повторяться до тех пор, пока все возможные комбинации не будут найдены или пока задача не будет решена.

Таким образом, эти четыре основных шага — выбор, проверка, откат и продолжение - являются ключевыми компонентами алгоритма backtracking. Каждый из этих шагов играет важную роль в нахождении всех комбинаций и оптимальных решений задач комбинаторной оптимизации.

Реализация алгоритма backtracking

1. Реализация алгоритма backtracking для решения задачи коммивояжера:

def tsp_backtracking(graph, path, visited, n, curr_cost, min_cost):

if len(path) == n:

        return curr_cost + graph[path[-1]][path[0]]  # Замкнуть путь

    for i in range(n):

        if not visited[i]:

            path.append(i)

            visited[i] = True

            new_cost = curr_cost + graph[path[-2]][i]

            if new_cost < min_cost:

                min_cost = tsp_backtracking(graph, path, visited, n, new_cost, min_cost)

            path.pop()

            visited[i] = False

    return min_cost

def solve_tsp(graph):

    n = len(graph)

    visited = [False] * n

    visited[0] = True

    path = [0]

    min_cost = float('inf')

    min_cost = tsp_backtracking(graph, path, visited, n, 0, min_cost)

    return min_cost

В этом примере мы имеем набор городов и матрицу с расстояниями между городами. Цель состоит в том, чтобы найти кратчайший путь, проходящий через каждый город один раз, и вернуть общую стоимость пути. Мы используем рекурсивную функцию tsp_backtracking, которая ищет оптимальный путь, добавляя по одному городу на каждой итерации. Мы используем отметки visited, чтобы знать, какие города уже посещены. Если мы достигаем конца пути (все города посещены), мы замыкаем его (добавляем расстояние от последнего города до начального) и сравниваем общую стоимость пути с текущим минимальным путем min_cost, обновляя его, если текущий путь лучше. Затем мы отменяем последний город и продолжаем поиск других возможных комбинаций городов. В конце мы возвращаем общую минимальную стоимость найденного пути min_cost.

2. Реализация алгоритма backtracking для генерации всех комбинаций из списка чисел с заданной суммой:

def generate_combinations(arr, target_sum, curr_sum, path, result):

if curr_sum > target_sum:

        return

    if curr_sum == target_sum:

        result.append(path.copy())

        return

    for i in range(len(arr)):

        curr_num = arr[i]

        curr_sum += curr_num

        path.append(curr_num)

        generate_combinations(arr[i:], target_sum, curr_sum, path, result)

        curr_sum -= curr_num

        path.pop()

def find_combinations(arr, target_sum):

    result = []

    generate_combinations(arr, target_sum, 0, [], result)

    return result

Этот пример решает задачу нахождения всех комбинаций чисел из данного списка, которые в сумме дают заданное число. Мы используем рекурсивную функцию generate_combinations, которая пробует все возможные комбинации, начиная с каждого числа в списке. На каждом шаге мы добавляем текущее число к текущей сумме и пути, затем рекурсивно вызываем функцию, продолжая генерацию комбинаций с оставшимся списком чисел и увеличившейся суммой. Если текущая сумма равна заданной сумме, мы добавляем текущий путь в результат. После этого мы отменяем последний добавленный элемент и продолжаем поиск других комбинаций. В конце мы возвращаем все найденные комбинации чисел.

3. Реализация алгоритма backtracking для решения головоломки Sudoku:

def is_valid(board, num, row, col):

# Проверка, что число num не встречается в текущей строке

    for i in range(9):

        if board[row][i] == num:

            return False

    # Проверка, что число num не встречается в текущем столбце

    for i in range(9):

        if board[i][col] == num:

            return False

    # Проверка, что число num не встречается в текущем подквадрате 3x3

    start_row = row - row % 3

    start_col = col - col % 3

    for i in range(3):

        for j in range(3):

            if board[i + start_row][j + start_col] == num:

                return False

    return True

def solve_sudoku(board):

    for row in range(9):

        for col in range(9):

            if board[row][col] == 0:  # Найти пустую ячейку

                for num in range(1, 10):

                    if is_valid(board, num, row, col):

                        board[row][col] = num  # Попробовать заполнить числом

                        if solve_sudoku(board):  # Рекурсивный вызов

                            return True

                        board[row][col] = 0  # Отмена хода если не удалось решить

                return False

    return True

В данном примере представлена реализация алгоритма backtracking для решения головоломки Sudoku. Мы рекурсивно пробуем заполнять пустые ячейки квадратной матрицы с цифрами от 1 до 9. На каждом шаге мы проверяем, является ли текущая цифра num допустимой для размещения в текущей ячейке. Проверка выполняется с помощью вспомогательной функции is_valid, которая проверяет отсутствие повторений num в текущей строке, столбце и 3x3 подквадрате, в котором находится текущая ячейка. Если num является допустимым, мы заменяем пустую ячейку на num и рекурсивно вызываем функцию для следующей пустой ячейки. Если рекурсивный вызов возвращает True (т.е. успешно решает головоломку), мы возвращаем True. Если рекурсивный вызов не удается решить головоломку, мы отменяем текущее заполнение ячейки (устанавливаем значение на 0) и продолжаем перебирать другие варианты. Если на одном из шагов все возможные варианты просмотрены и головоломка остается нерешенной, мы возвращаем False для отката на предыдущий уровень и попытку других комбинаций чисел. В конце выполнения функции, если головоломка успешно решена, мы возвращаем True.

Ограничения алгоритма backtracking

При работе с большими наборами данных, алгоритм backtracking может столкнуться с серьезными ограничениями временной сложности. В зависимости от конкретной задачи и набора данных, алгоритм может потребовать экспоненциального времени выполнения, что делает его непрактичным или даже невозможным для использования.

Чтобы преодолеть эти ограничения, существуют различные методы оптимизации алгоритма backtracking. Вот несколько из них:

1. Ограничение вариантов выбора:Вместо попытки поиска всех возможных комбинаций, можно предварительно ограничить число вариантов, которые нужно рассмотреть. Например, можно использовать некоторые эвристики или сортировку данных, чтобы отсеять некоторые неоптимальные варианты.

2. Удаление дубликатов: В некоторых случаях, алгоритм backtracking может генерировать дубликаты решений. Это может привести к повторному перебору тех же самых вариантов и существенно увеличить временную сложность. Путем использования хэш-таблицы или других соответствующих структур данных можно эффективно удалять дубликаты и избежать повторных операций.

3. Подсчет оценок и отсечение ветвей: Даже если алгоритм backtracking перебирает все варианты, можно использовать оценки или эвристики для определения более перспективных ветвей, которые имеют более высокий потенциал для достижения оптимального решения. Тем самым, можно отсекать не перспективные варианты и сократить количество операций.

4. Мемоизация результатов: Если алгоритм backtracking оказывается рекурсивным, то результаты предыдущих подзадач можно запомнить и повторно использовать позже. Это позволяет избежать повторного пересчета, что уменьшает размер пространства поиска и значительно улучшает производительность алгоритма.

5. Параллельное выполнение: В некоторых случаях, алгоритм backtracking может быть разбит на независимые задачи, которые могут выполняться параллельно. Путем распараллеливания алгоритма, можно значительно сократить время выполнения и улучшить производительность.

Безусловно, выбор методов оптимизации для алгоритма backtracking зависит от конкретной задачи и набора данных. Очень часто необходимо провести некоторые эксперименты и анализ, чтобы определить самые эффективные способы оптимизации.

Заключение

Итак, подводя итог, алгоритм backtracking является незаменимым инструментом для разработчиков, необходимым для нахождения всех возможных комбинаций в наборе данных. Этот метод открывает новые возможности в решении задач комбинаторики, что делает его пригодным для применения в различных областях разработки программного обеспечения. Отличительной особенностью алгоритма является его мощность и эффективность при работе с большими объемами данных.

17 июля в OTUS пройдет открытое занятие «Бор Ахо-Корасика». На этом вебинаре мы познакомимся с остроумным алгоритмом Ахо-Корасика для поиска нескольких шаблонов в тексте. Для этого мы создадим недетерминированный конечный автомат в виде префиксного дерева, добавим суффиксные и финальные ссылки, вместе пропустим текст через этот Бор и найдём все шаблоны за линейное время, реализовав алгоритм Ахо-Корасика.

• Записаться на открытый урок