И это не пузырьковая, а нечто гораздо более тупое.
Как-то после обеда, стоя в коридоре с чашечкой кофе, мне пришла в голову мысль. Что ведь для того, чтобы убедиться, что массив отсортирован, надо сделать всего n-1 сравнение. Например, для массива длины 4 таких сравнения будет 3:
if (a0 < a1 < a2 < a3) А получив утвердительный ответ на этот вопрос, мы можем сразу вернуть готовый массив:
if (a0 < a1 && a1 < a2 && a2 < a3) return [a0, a1, a2, a3];Клево! Теперь чтобы превратить это в сортировку 4 чисел осталось просто проверить все остальные комбинации максимально тупым образом:
def sort4(a0, a1, a2, a3) {
if (a0 < a1 && a1 < a2 && a2 < a3) return [a0, a1, a2, a3];
if (a0 < a1 && a1 < a2 && a3 < a2) return [a0, a1, a3, a2];
if (a0 < a2 && a2 < a1 && a1 < a3) return [a0, a2, a1, a3];
...
}
Оговорка
Строго говоря для того чтобы наша сортировка была стабильной, везде надо писать "<=" (меньше или равно), но меня задолбало это это набирать, так что я буду везде писать только "<". Упражнение по превращению этого удовольствия в продакшен-код я оставляю читателю.
Сколько таких комбинаций? Ну это легко. Их ровно 4! = 24. Мы только что придумали алгоритм с вычислительной сложностью O(n*n!). Это гораздо хуже пузырьковой сортировки (с его квадратичной асимптотикой) не только из-за ужасающе долгой работы, но и еще в добавок нам для массива каждой длины надо писать отдельную функцию. Жуть.
А факториал растет очень быстро, значит наши функции будут становиться все длиннее, отнимая не только вычисления, но и память - ее нам тоже потребуется O(n!). Не для хранения данных (мы же их даже никуда не сохраняем), а для самого алгоритма. Для всех "обычных" алгоритмов размер кода фиксирован, то есть O(1), и мы его просто игнорируем при оценке асимптотики по памяти. Для нашей "тупой" сортировки такое не прокатит.
Но давайте немного поразмышляем. Видим, что первые 3 случая повторяются в части нескольких первых сравнений. А что, если...
if a0 < a1:
if a1 < a2:
if a2 < a3:
return [a0, a1, a2, a3]
else:
if a1 < a3:
return [a0, a1, a3, a2]
else:
...
else:
...
....Хм. Давайте снова посчитаем вычислительную сложность. Кажется мы тут все наши возможные комбинации каждым сравнением делим примерно на 2. То есть вычислительная сложность сразу получает себе суперспособность логарифм: O(log(n!)).
То есть, если мы все правильно поняли, то мы только что придумали алгоритм, который сортированные списки обрабатывает за O(n) (самая первая ветка срабатывает за n-1 сравнение), а остальные случаи мы сортируем не хуже теоретически идеального случая. То есть как Quicksort, только без его "худшего" случая, когда он деградирует до "пузырька".

Расчехляем питон и пишем туда наш генератор тупых сортировок. Для начала возьмем и напишем функцию генерации перестановок:
def permutations(a: list[int]) -> list[list[int]]:
if len(a) == 1:
return [a]
return [
[a[i]] + recur
for i in range(len(a))
for recur in permutations(a[0:i] + a[i + 1:])
]Потом выкинем ее, вспомнив, что уже есть itertools.permutation() который делает ровно то же самое.
Теперь пишем 2 функции генерации строк:
def gen_comp(indent: int, l: int, r: int, s_then: str, s_else: str):
ind = "\t" * indent
return ind + f"if a{l} < a{r}:\n{s_then}\n{ind}else:\n{s_else}"
def gen_return(indent: int, indice: list[int]):
return "\t" * indent + f"return [" + ", ".join([f"a{i}" for i in indice]) + "]"
Ну и саму функцию строящую дерево сравнений (осторожно, говнокод):
def gen_sort_n(cases: list[list[int]], known: list[tuple[int, int]], indent):
c = cases[0]
if len(cases) == 1:
return gen_return(indent, c)
lss, gtr = [], []
for l, r in list(zip(c, c[1:])):
if l == r or (l, r) in known or (r, l) in known:
continue
for c in cases:
(lss, gtr)[c.index(l) > c.index(r)].append(c) # Хитрый трюк с заполнением двух массивов за раз.
s_then = gen_sort_n(lss, known + [(l, r)], indent + 1)
s_else = gen_sort_n(gtr, known + [(r, l)], indent + 1)
return gen_comp(indent, l, r, s_then, s_else)
print(gen_sort_n(list(itertools.permutations(range(4))), [],0))
Она просто берет первую перестановку из переданных и сравнивает первую непроверенную пару элементов в ней. Потом все оставшиеся случаи раскидывает по подветкам true и false рекурсивно. Получаем на выходе код:
Много кода
if a0 < a1:
if a1 < a2:
if a2 < a3:
return [a0, a1, a2, a3]
else:
if a1 < a3:
return [a0, a1, a3, a2]
else:
if a0 < a3:
return [a0, a3, a1, a2]
else:
return [a3, a0, a1, a2]
else:
if a0 < a2:
if a1 < a3:
return [a0, a2, a1, a3]
else:
if a2 < a3:
return [a0, a2, a3, a1]
else:
if a0 < a3:
return [a0, a3, a2, a1]
else:
return [a3, a0, a2, a1]
else:
if a1 < a3:
return [a2, a0, a1, a3]
else:
if a0 < a3:
return [a2, a0, a3, a1]
else:
if a2 < a3:
return [a2, a3, a0, a1]
else:
return [a3, a2, a0, a1]
else:
if a0 < a2:
if a2 < a3:
return [a1, a0, a2, a3]
else:
if a0 < a3:
return [a1, a0, a3, a2]
else:
if a1 < a3:
return [a1, a3, a0, a2]
else:
return [a3, a1, a0, a2]
else:
if a1 < a2:
if a0 < a3:
return [a1, a2, a0, a3]
else:
if a2 < a3:
return [a1, a2, a3, a0]
else:
if a1 < a3:
return [a1, a3, a2, a0]
else:
return [a3, a1, a2, a0]
else:
if a0 < a3:
return [a2, a1, a0, a3]
else:
if a1 < a3:
return [a2, a1, a3, a0]
else:
if a2 < a3:
return [a2, a3, a1, a0]
else:
return [a3, a2, a1, a0]Выглядит вроде неплохо. А давайте посчитаем, какая средняя глубина вложенности if-ов при увеличении n. Для этого для каждого вызова gen_return запомним ident и просто посчитаем среднее. Код я тут опускаю, потому что он скучный, а терпение читателя не резиновое.
n |
n! |
Avg(indent) |
2 |
2 |
1.000 |
3 |
6 |
2.667 |
4 |
24 |
4.917 |
5 |
120 |
7.717 |
6 |
720 |
11.050 |
7 |
5040 |
14.907 |
8 |
40320 |
19.282 |
Давайте посмотрим, как эти числа ложатся на теорию.

Что-то тут не так. Минимальная глубина, как и ожидалось, очень приятная = n-1, но вот оранжевая линия (средняя глубина) выше наших ожиданий. Мы же хотели O(n*logn), а тут явно что-то другое. Давайте внимательнее посмотрим на сгенеренный код. Некоторые перестановки (например return [a0, a3, a2, a1]) возвращаются только после 6 сравнений, тогда как теория предсказывает что их должно быть не больше 5 (столько сделает mergesort в худшем случае сортировки массива из 4 элеменов). Видно что это происходит из-за того что наши деревья сравнений не сбалансированы. То есть они не всегда делят количество вариантов пополам. Иногда пропорции оказываются гораздо хуже: 1 к 3 или даже 1 к 7. Так не пойдет. Давайте дерево балансировать.
Для этого переберем разные сравнения из доступных и выберем то, которое делит все случаи наилучшим образом (в пропорции 1:1).
Секретные материалы
Тут был график, который я где-то пролюбил, а заново искать и перезапускать старый код мне лень. Поэтому я прошу читателя мне поверить на слово, что там все было так, как описано ниже. А сам график был прекрасен как никогда так же скучен, как и первый, так что уважаемый читатель ничего не потерял. :-/
Статистика улучшилась, но опять не дотягивает до "идеальной". Еще немного поразмыслив, понимаем, что выбор "лучшего" доступного сравнения на данном шаге может привести к тому что, оставшиеся после деления варианты уже невозможно поделить поровну внутри рекурсивных вызовов.
Давайте тогда перепишем код чтобы он перебрал вообще все возможные последовательности проверок и вернул самую сбалансированную. Надо сказать, что такой перебор ужасно тормозит так как сложность такой генерации растет как квадрат факториала. Ради науки мы потерпим. Но только до n=5.
N |
depth |
2 |
[1, 1] |
3 |
[2, 3, 3, 2, 3, 3] |
4 |
[4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5] |
5 |
[7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 6, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 6, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 6, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 6, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 6, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 6, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 6, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 6, 7, 7] |
Ну вот, совсем другое дело. Теперь взглянем на сгенеренный код для n=4.
if a0 < a1: # Ага...
if a1 < a2: # ага...
if a1 < a3: # Штоа?!?
if a2 < a3: # а! вот оно чо.
return [a0, a1, a2, a3]
else:
return [a0, a1, a3, a2]
else:
if a0 < a3:
return [a0, a3, a1, a2]
else:
return [a3, a0, a1, a2]
else:
...Хм. Наша красивая первая "перестановка" теперь вместо 3 сравнений содержит 4. Причем "лишнее" сравнение (третье по счету) выглядит как-то совсем ненатурально. Однако статистика не врет - этот способ проверки самый лучший для среднего случая.
Но для среднего случая уже есть сортировка слиянием. Она гарантирует всегда близкое к идеальному количество сравнений. Лучше него только алгоритм слиянием-вставками и его вариации. Все они с фиксированным размером кода. Так нафига козе баян?
Дальше хуже
Для n=5 таких "ненужных" сравнений (для тривильного случая упорядоченнго массива) уже 7-4=3:
if a0 < a1:
if a2 < a3:
if a0 < a2:
if a2 < a4:
if a3 < a4:
if a1 < a3:
if a1 < a2:
return [a0, a1, a2, a3, a4]
else:
return [a0, a2, a1, a3, a4]
else:
if a1 < a4:
return [a0, a2, a3, a1, a4]
else:
return [a0, a2, a3, a4, a1]
else:
...Но можно подобрать параметры для оптимизации чтобы снизить это количество до 2.
И вот тут кажется мы можем нащупать какую-то пользу из нашего эксперимента. Мы получили действую модель оптимизации алгоритма под исходные данные. Если мы что-то знаем про частотность перестановок в исходных данных, мы можем подогнать под них алгоритм сортировки и получить гарантированно самую быструю сортировку. Быстрее теоретических чисел сортировки.
"Погодите-погодите" - скажет кто-то наивный - "ведь мы по прежнему имеем ужасную асимптотику по памяти и надо писать отдельную функцию для каждого n". На что мы имеем возразить:
Во первых очевидно, что его можно использовать только для небольших n. Вероятно не больше 7-8. После чего сгенеренный код начнет занимать уже непрактично много места. А если мы ограничиваем размер массива, то код становится конечным и наше использование памяти возвращается в приятное O(1).
Для больших n мы можем "сверху" на него надстроить обычную сортировку слиянием. Тем самым сильно ускорив сортировку для наших данных, а не сферических в вакууме.
Похожий трюк с подменой алгоритмов для сортировки массивов разной длины делают многие библиотеки. Скажем, заменяя на коротких массивах quicksort пузырьком потому что второй не использует рекурсию и начинает обгонять первого за счет меньшего оверхеда.
В качестве дальнейшей оптимизации нашего "супер-алгоритма" можно предложить:
Вместо возврата массивов генерить готовые операции in-place обмена элементов массива самым оптимальным образом (сдвигая подмассивы, где возможно, вместо перемещения поштучно). Либо делая идеальные циклические перестановки с единственным слотом:
temp = a0; a0 = a3; a3 = a2; a2 = tempдля варианта [a3, a1, a0, a2]) и т.п.Избавлять от ветвлений с помощью трюков branchless programming, переходя на векторные инструкции. Это должно дополнительно ускорять в разы и десятки раз.
На том и закончим наши размышления у кофе-машины и пойдем работать дальше, оставив задачу конечной реализации данного прорывного алгоритма студенту, которому нужна идея для курсовой...
Комментарии (38)

Zara6502
19.08.2023 03:41+12И вот тут кажется мы можем нащупать какую-то пользу из нашего эксперимента. Мы получили действую модель оптимизации алгоритма под исходные данные. Если мы что-то знаем про частотность перестановок в исходных данных, мы можем подогнать под них алгоритм сортировки и получить гарантированно самую быструю сортировку. Быстрее теоретических чисел сортировки.
Ну вот, а когда я пишу что сортировка зависит от контекста данных (да и не только сортировка, но и кодирование, сжатие и т.д.), то меня закидывают ссаными тряпками, мол не трогай святое пользуйся универсальными методами и вообще, если метод не универсальный и не стабильный то он фуфуфу.
Но эти же люди продолжают пользоваться архиваторами видимо забывая как именно устроены ключи степени сжатия в самой программе и почему контекст важен.

Tasta_Blud
19.08.2023 03:41+2и при этом люди забывают, что контекст важен. это единица информации, которая идёт с архивом вместе с данными - насколько оптимально был упакован архив.универсальные алгоритмы всегда проигрывают специфичным именно потому, что у них нет либо они игнорируют эту информацию.
поскольку даже мне, только поверхностно изучавшей теорию информации 10 лет назад в университете, понятно, что более продвинутые алгоритмы сначала анализируют входную информацию, чтобы подобрать более подходящий метод сжатия. если бы это было не так - мы бы до сих пор пользовались бы каким-нибудь rle, в худшем случае - по теореме Шеннона (zip в основной модификации)
а потому современные упаковщики, сначала смотрят тип данных для упаковки, а потом выбирают стратегию упаковки именно исходя из полученного анализа

BugM
19.08.2023 03:41+1а потому современные упаковщики, сначала смотрят тип данных для упаковки, а потом выбирают стратегию упаковки именно исходя из полученного анализа
Нет же. Они гонят все в gzip или те что более продвинутые в zstd. И не парятся.

Zara6502
19.08.2023 03:41не совсем так. тут вопрос скорее бизнес модели. но крупные компании типа амазона или гугла заморачиваются по поводу контекстного сжатия.
кстати PNG по сути как раз сжимает данные в зависимости от контекста, а вот насколько хорошо, то уже зависит от реализации, поэтому я обычно за paint.net и photoshop еще файлы дожимаю с помощью Pingo. У меня на сетевом диске есть библиотека PNG файлов для рисования всякого, размер около 4 Гб, я прогнал как-то ее через Pingo и уменьшил размер до 3.2Гб.

BugM
19.08.2023 03:41Подобрать более подходящий алгоритм под паттерн данных на стадии проектирования можно. И так делают иногда. Хотя как правило все равно просто берут gzip или zstd.
Это все равно безмерно далеко от анализа текущего потока и подбора чего-то под него. Один раз спроектировали, написали и оно крутится годами.
PS: Правильная настройка словаря для zstd дает больше чем практически все остальное (работающее со сравнимой скоростью) на почти любом паттерне данных.

Zara6502
19.08.2023 03:41настройка словаря - это и есть контекстная настройка, каким методом вы решили задачу не так важно. я вам писал ответ на ваши "берут gzip и не парятся", а вы тут же пишете что "настраивают словарь", то есть заморочились таки.

BugM
19.08.2023 03:41В подавляющем большинстве случаев берут гзип и не парятся. Оно того не стоит. В остальных случаях стоит подумать о чем-то вроде настройки словаря zstd.
И это все равно не "сначала смотрят тип данных для упаковки, а потом выбирают стратегию упаковки именно исходя из полученного анализа".

Zara6502
19.08.2023 03:41То что кто-то не слишком умный это понятно, но мы же не такие, а значит выбор стратегии имеет место быть. Ну и разговор идёт об обычных архиваторах, а не о бизнес-моделях, а там zip/7z/rar где Deflate совсем не единственный метод, скорее уж вы попадёте на LZMA.
Лично я для себя пользуюсь zpaq (m5) и 7zip(bzip2 или ppmd) и за 50 лет ни разу не пользовался ни gzip ни zstd.

Zara6502
19.08.2023 03:41ну я что-то не припомню чтобы популярные архиваторы занимались анализом данных (ниже напишу). я говорю о том что степень сжатия, которая обозначена в настройках архиватора это не какой-то очень умный алгоритм, а просто выбор набора алгоритмов меняющих соотношение сильная_степень_сжатия/скорость.
касательно контекста, есть например архиватор zpaq, у него используется контекстная модель. тут да - достигается повышение степени сжатия за счет анализа данных, но сжимает он долго. основный архиваторы крутятся вокруг словарных методов и в большинстве своем на первое место ставятся или скорость или количество используемой памяти.
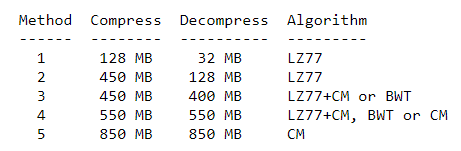
zpaq

vk6677
19.08.2023 03:41+7Пример тупой сортировки (не стоит её повторять):
#include
#define N 10
int main()
{
int vec[N] = {1, 7, 3, -7, -1, 7, 9, -2, 5, 8};
for (auto i = 0; i < N - 1; ++i)
if ((vec[i] > vec[i + 1])) {
std::swap(vec[i], vec[i + 1]); i = -1;
}
for (auto i = 0; i < N; ++i) std::cout << vec[i] << "\t";
return EXIT_SUCCESS;
}
haqreu
19.08.2023 03:41+2Никак не пойму, зачем писать auto i =0? int и на один символ короче, и нагляднее...

Chuvi
19.08.2023 03:41+12
dyadyaSerezha
19.08.2023 03:41Блин, как начал читать статью, тут же подумал об этом алгоритме, но оказалось, что его уже придумали (

NooneAtAll3
19.08.2023 03:41Я больше SlowSort предпочитаю
никакого рандома
экспоненциальная сложность

Wan-Derer
19.08.2023 03:41Моя номинация на самую тупую сортировку:
Java
import java.util.Arrays; public class Test { public static void main(String[] args) { final int[] arr = {1, 7, 3, -7, -1, 7, 9, -2, 5, 8}; final int[] sorted = naiveSort(arr); System.out.println(Arrays.toString(arr)); System.out.println(testSorted(arr)); System.out.println(Arrays.toString(sorted)); System.out.println(testSorted(sorted)); } private static int[] naiveSort(int[] arr) { final int[] sorted = new int[arr.length]; final boolean[] checked = new boolean[arr.length]; Arrays.fill(checked, false); for (int i = 0; i < arr.length; i++) { sorted[i] = findMin(arr, checked); } return sorted; } private static int findMin(int[] arr, boolean[] checked) { int min = Integer.MAX_VALUE; int minInd = 0; for (int i = 0; i < arr.length; i++) { if (!checked[i] && arr[i] <= min) { min = arr[i]; minInd = i; } } checked[minInd] = true; return min; } private static String testSorted(int[] arr) { for (int i = 0; i < arr.length - 1; i++) { if (arr[i] > arr[i + 1]) { return "Array is not sorted"; } } return "Array is sorted"; } }Хотя это скорее не тупая, а "наивная". Т.е. если бы я ничего не знал о программировании (ну, кроме синтаксиса), я бы написал именно так. Даже то что можно просто поменять местами два элемента - это какая-то иезуитская хитрость :) Я бы наверно сам не допёр, по крайней мере, не сразу.

alexxisr
19.08.2023 03:41+1это ж по сути сортировка выбором, только складывают не в отдельный массив, а в начало/конец сортируемого, сдвигая неотсортированное.
Но это самый естественный способ сортировать, по-моему все кто еще не знает алгоритмы сортировки делают что-то наподобие этого.

barbalion Автор
19.08.2023 03:41+1Это сортировка выбором (selection sort). Добавить немного улучшений в часть
findMinи сразу получите heapsort.

Sergey1124
19.08.2023 03:41+4У меня самый простой вариант:
public void sort(List<Integer> list) { while (!isSorted(list)) { Collections.shuffle(list); } } private boolean isSorted(List<Integer> list) { for (int i = 0; i < list.size() - 1; i++) { if (list.get(i) > list.get(i + 1)) return false; } return true; }

JekaMas
19.08.2023 03:41+2Отличный вариант! Но персонально останусь верен O(n) StalinSort https://github.com/gustavo-depaula/stalin-sort

redfox0
19.08.2023 03:41+2Конечно, это юмористическая статья, но подобная сортировка оптимизированная под размер массива (4-9 элементов) существует в прод-коде. Если не изменяет память, разработчики гугла применили такое в одной из библиотек и увеличили скорость сортировки внутри sql-запросов до 30 %.
Реализация libcxx обрабатывала несколько конкретных случаев особым образом. Коллекции длиной 5 или меньше сортировались при помощи специальных самописных сортировок на основе сравнений.
https://habr.com/ru/articles/662181/
barbalion Автор
19.08.2023 03:41Вероятно вы правы. Не удивительно. Идея же лежит на поверхности.

uszer
19.08.2023 03:41Адаптивное сжатие, зависящее от контекста - оно же в полный рост используется во всём, что использует вейвлеты. Там для каждого типа "сигнала" подбирается соответствующий вейвлет и количество коэффициентов, обращающихся в "0" или близких к "0" (которые можно отбросить) от этого увеличивается.

gchebanov
19.08.2023 03:41+2который я где-то пролюбил
fixed. Вот среднее число сравнений если каждый раз выбирать индексы жадно (максимизируя min(len(lss), len(gtr)). Было бы хорошо если бы обновили график.
ссылка на код
[1.0, 2.6666666666666665, 4.666666666666667, 6.933333333333334, 9.577777777777778, 12.39047619047619, 15.406795634920634]более тупое
Тут автор весьма принижает свои размышления, ведь на самом деле речь не о поиске сортирующей перестановки без дополнительно памяти, а вполне себе серьезный математический вопрос:
какое наименьше (в среднем) число вопросов (сравнений двух элементов) нужно задать что бы отгадать загаданную перестановку

Vitaly48
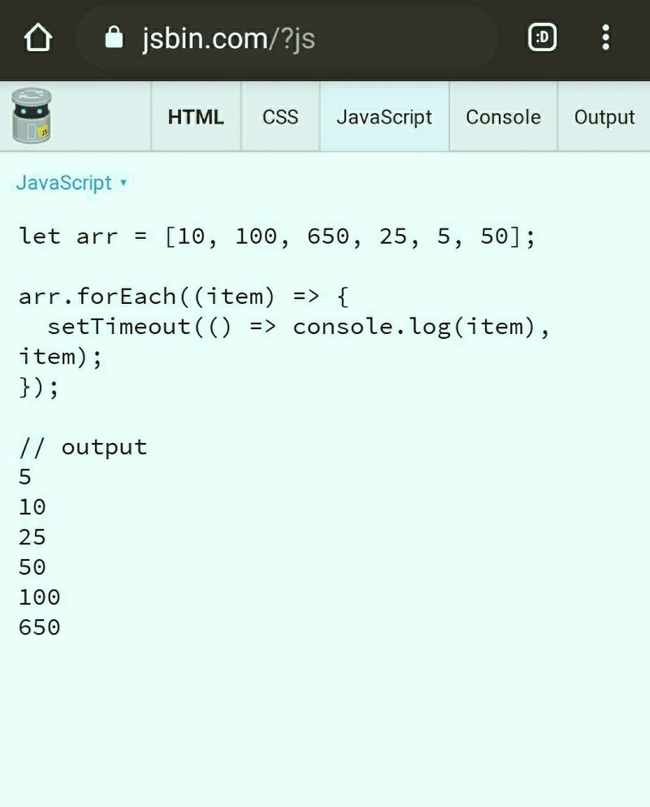
19.08.2023 03:41+14Подержите моё пиво

commanderxo
19.08.2023 03:41+4Гениально! В то время как лучшие умы человечества пытаются превзойти n log n, этот код при сортировке отрицательных чисел должен выдать ответ ещё до вызова!

Mad__Max
19.08.2023 03:41+2О, когда весной изучал работу нового поколения псевдоразумных нейросетей архитектуры трансформера (GPT3 / GPT 4 и их многочисленные аналоги), в частности остановился на том, как они сортируют списки или занимаются простым счетом если задать им такую задачу в чистом виде или как часть более общей.
В частности что они без проблем справляются с короткими списками, но начинают ошибаться и сильно тупить (даже если указывать им на ошибки и пытаться помочь/подсказать) если список становится длиннее (в зависимости от конкретной реализации и "размера" сети = количества ее "параметров"/весов, это происходит где-то в диапазоне от 7-10 элементов и до нескольких десятков)
И пришел к выводу, что нейросети в процессе "тренировки" самостоятельно сформировали внутри себя очень специфические алгоритмы. Которые скорее всего представляют что-то очень похожее на описанное вами! Конкретно для случая сортировки.Вот тут про это немного писал в комментариях:
https://habr.com/ru/companies/ods/articles/716918/comments/#comment_25509482
https://habr.com/articles/729966/#comment_25509056 (тут 1й пример, где прошу нейросеть на базе GPT-4 отсортировать буквы по алфавиту)Что-то похожее(хотя и немного другое) происходит и с математическими операциями, когда подобная нейросеть пытается выполнять математические операции — там размерность чисел не ограничена, но результат получается "примерный".
Из-за того, что такие нейросети класса "большая текстовая модель", в частности Трансформер имеют очень жесткие исходные(архитектурные) ограничения: они не рекуррентные (т.е. прямые циклы или даже их иналоги в их внутренних алгоритмах просто невозможны, но зато возможны множественные и очень сложные ветвления и проверки условий!), у них нет "рабочей памяти" для хранения переменных(память и слежение за контекстом разговора чат-ботов на основе таких сетей реализуется внешними алгоритмами, подающими часть истории разговора на вход нейросети заново при каждом следующем сообщении/запросе).
То при достаточном уровне тренировки и размере сети (количестве параметров представляющих собой аналог объема кода) в ней рождаются вот такие вот "тупые" алгоритмы. В частности для сортировки и подсчета элементов. Не по принципу "тупости", а "жить захочешь, еще не так раскорячишься" (с).
Вот представьте, что вы программируете, но у вас в распоряжении есть только один очень дурацкий язык программирования, в котором ВООБЩЕ отсутствуют циклы и нет доступа к оперативной памяти для хранения переменных(зато констант прямо в код нафигачить можно почти неограниченно) и даже встроенных базовых математический операций(сложение, умножение и т.д.) в языке нет. Но зато if… then… else и их аналоги (Case, Select и т.д.) можно фигачить в код тоже почти в неограниченных количествах.
И вам вот с таким "инструментарием" нужно отсортировать массив, или сосчитать количество элементов в некотором множестве или выполнять математические операции и т.д.И вот тогда, подобные "тупые" алгоритмы, окажутся далеко неплохим вариантом, а вероятно одним из лучшим (из возможных в конкртеных ограниченных условиях). А вот это:
А факториал растет очень быстро, значит наши функции будут становиться все длиннее, отнимая не только вычисления, но и память — ее нам тоже потребуется O(n!). Не для хранения данных (мы же их даже никуда не сохраняем), а для самого алгоритма.
Становится не багой (простыни говнокода из бесконечной лапши IF-ов, вместо считанных байт для хранения нескольких переменных и обработки в цикле и вызова функций рекурсией), а киллер-фичей в условиях когда этих самых байт ОЗУ тупо нет в принципе (точнее не можем в него ничего писать во время исполнения "кода"), зато мегабайты кода — вообще не проблема.

wataru
19.08.2023 03:41Самая крутая сортировка — квантовая. Имея квантовый источник случайного шума, можно за O(n) получить случайную перестановку массива. Потом, опять же за O(n), можно, как верно заметил автор, проверить, а не отсортирован ли массив. Если нет, то надо, всего-лишь уничтожить вселенную. В результате (если принять многомировую интерпретацию квантовой физики) останется хотя бы одна вселенная, в которой массив отсортирован за O(n). Вот, мы и изобрели линейный алгоритм сортировки!




Zara6502
Браво. Читал с удовольствием.
Ну есть же замена в редакторе, это быстро.