
В одном из своих предыдущих постов под названием "Эйлер, Чёрч и Мандельброт — этюд о красоте и математике" я немного затронул тему рассмотрения функционального программирования в качестве основы реальности. Под тем постом было оставлено множество интересных комментариев, один из которых, написанный @nickolaym, вдохновил меня на развитие мысли в данном направлении. Так появился этот пост, в котором прямо как во времена пифагорейской школы и платоновской академии философия переплелась с математикой, а математика с философией.
Мир как фикция, мир как функция
Миру присуще непостоянство: рождаются и умирают люди, строятся и разваливаются государства, появляются и исчезают целые цивилизации. Время, подобно олицетворяющему его древнегреческому богу Кроносу, пожирает собственных детей. Почти все языки программирования, созданные человечеством на заре компьютерной эры, не дожили до наших дней. Противостоять неумолимому течению реки времени смог только один из самых древних языков - LISP.
Его выживание - не простая удача, а следствие того факта, что LISP воплощает в себе фундаментальные принципы программирования, математики и, как вам станет ясно из этого поста, самого бытия. Создатель объектно-ориентированного программирования Алан Кей назвал LISP величайшим из когда-либо созданных языков программирования, а многие другие программисты с особым религиозным трепетом величают его не иначе как "язык Бога".
Я и сам долгие годы пытался создать идеальный язык программирования. Я брал за основу разные языки программирования и, как скульптор высекающий из камня прекрасную статую, отсекал от них всё лишнее, постепенно делая их всё более немногословными, целостными и мощными. Но какой бы язык я не брал за основу, в конце концов после отрезания всего лишнего я всегда получал один и тот же результат - LISP.
Оригинальный LISP был создан американским математиком Джоном Маккарти в конце 50-х годов XX века в качестве "физического" воплощения идей лямбда-исчисления - формального математического аппарата для описания вычислений, разработанного другим американским математиком - Алонзо Чёрчем. Идея лямбда-исчисления лежит в основе всей концепции функционального программирования, а LISP является эталонной реализацией этой концепции.
Суть функционального программирования можно изобразить в виде довольно простой схемы:
Данные -> Функция -> Данные
Данные - это представленные в виде последовательности битов числа, строки, значения истина/ложь, списки. Функция - это описанная математическим равенством зависимость выходных данных от одних или нескольких входных данных.
Примеры данных:
13
"Hello"
true
[1, 2, 3]Пример функции:
y = x + 1Основной постулат функционального программирования утверждает, что функции должны быть чистыми - то есть не иметь внутреннего состояния и всегда выдавать одинаковые выходные значения на одинаковые входные параметры. Как функция y=x+1 всегда выдает выходное значение y=3 при входном параметре x=2. Кроме того, в функциональном программировании не принято перезаписывать данные под одним и тем же именем - все данные определяются в виде констант:
// Переменная a - в функциональном программировании делать так нельзя
a = b + 1
a = a + 3
// Константа a - в функциональном программирование нужно делать так
a = b + 1
с = a + 3Математическая функция - не материальный объект, а бесплотная идея. Древнегреческий философ Платон считал, что наш физический мир представляет из себя лишь блёклую тень мира идей, освещаемых божественным светом. В материальном мире умирают люди, рушатся империи, погибают даже галактики, но два плюс два всегда без исключения равно четырём. Так было, так есть и так будет - эту вечную бессмертную идею никому не под силу изменить, она существует независимо от чего бы то ни было.
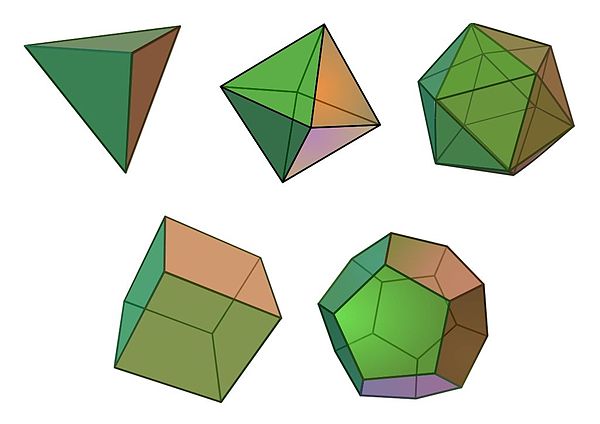
В пример вечности и независимости математических идей Платон обычно приводил правильные многогранники, которые теперь в его честь часто называют платоновыми телами. Правильный многогранник - это трехмерная геометрическая выпуклая фигура, состоящая из одинаковых многоугольников с равными сторонами. Ещё во времена Платона было доказано, что таких многогранников существует только пять: тетраэдр, гексаэдр (куб), октаэдр, додекаэдр и икосаэдр - даже могущественные олимпийские боги не в силах создать шестой. Такая независимость математических идей от воли людей и богов, по мнению Платона, доказывала то, что идеи - это самостоятельные объекты, существующие в своем особом "мире" идей.
Другой излюбленный пример Платона, иллюстрирующий его учение о материальном мире как тени мира идей - рассмотрение круга. Мы можем взять лист бумаги с карандашом и нарисовать множество кругов. Ни один из них не будет совершенно круглым, каждый будет чуточку отличаться от другого - то дрогнет рука, то движение недостаточно точное. Если мы попытаемся выточить круглый предмет на станке, то тоже не получим двух полностью одинаковых предметов. У каждого станка есть погрешность обработки - тут и там один кругляшок будет на пару микрометров отличаться от другого. Однако несмотря на то, что ни один материальный круг не совершенен, в каждом из них мы видим воплощение некого идеального круга. Поэтому можно сказать, что материальные круглые предметы - это тень идеи круга. Точно так же можно рассуждать о чем угодно другом: так, например, все столы в мире немного отличаются друг от друга, но все без исключения являются тенью идеи стола.
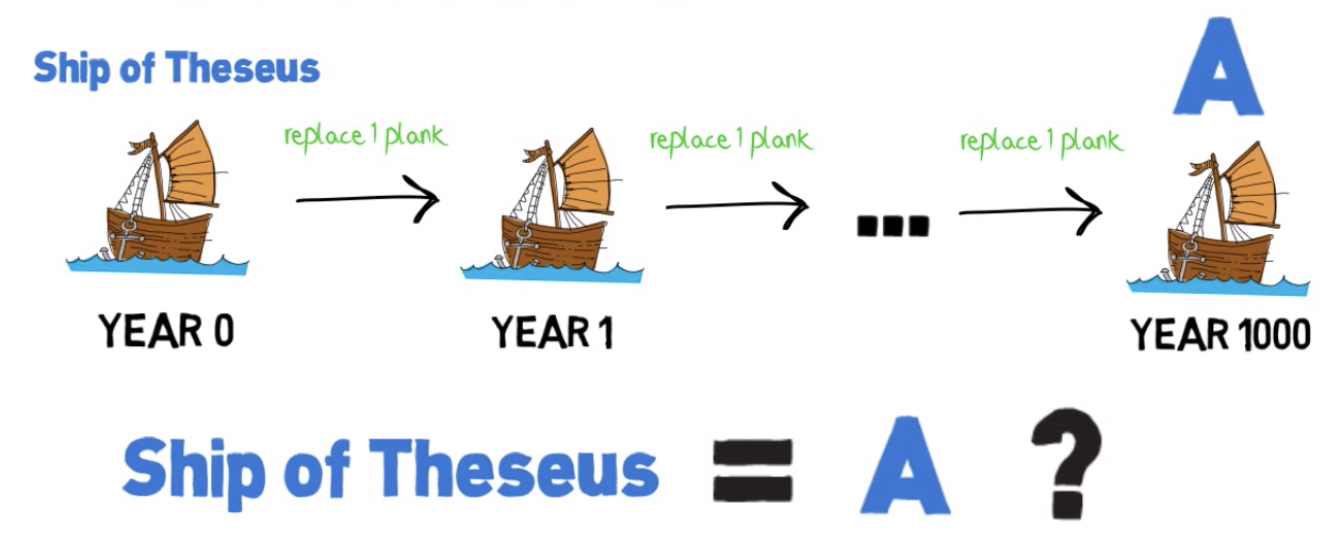
Ученик Платона, столь же знаменитый как и его учитель, философ Аристотель рассматривал мир под другим углом. В его картине мира идеи - это формы, которые придают материи определенный вид, превращают вещество в вещи. Идея стола как бы "склеивает" молекулы вещества, превращая их в материальный стол. Аристотелевскую связь между идеями и материей довольно просто понять на примере знаменитого философского парадокса корабля Тесея.
Согласно древнегреческой легенде, корабль, на котором мифологический герой Тесей вернулся с Крита после победы над Минотавром, использовался афинянами для ежегодного паломничества на остров Делос. Перед каждым плаванием корабль чинили, заменяя часть прогнивших досок на новые. Спустя какое-то время все старые доски корабля были заменены на новые. Среди людей разгорелся спор: тот же этот корабль, на котором плавал Тесей, или уже другой - новый?
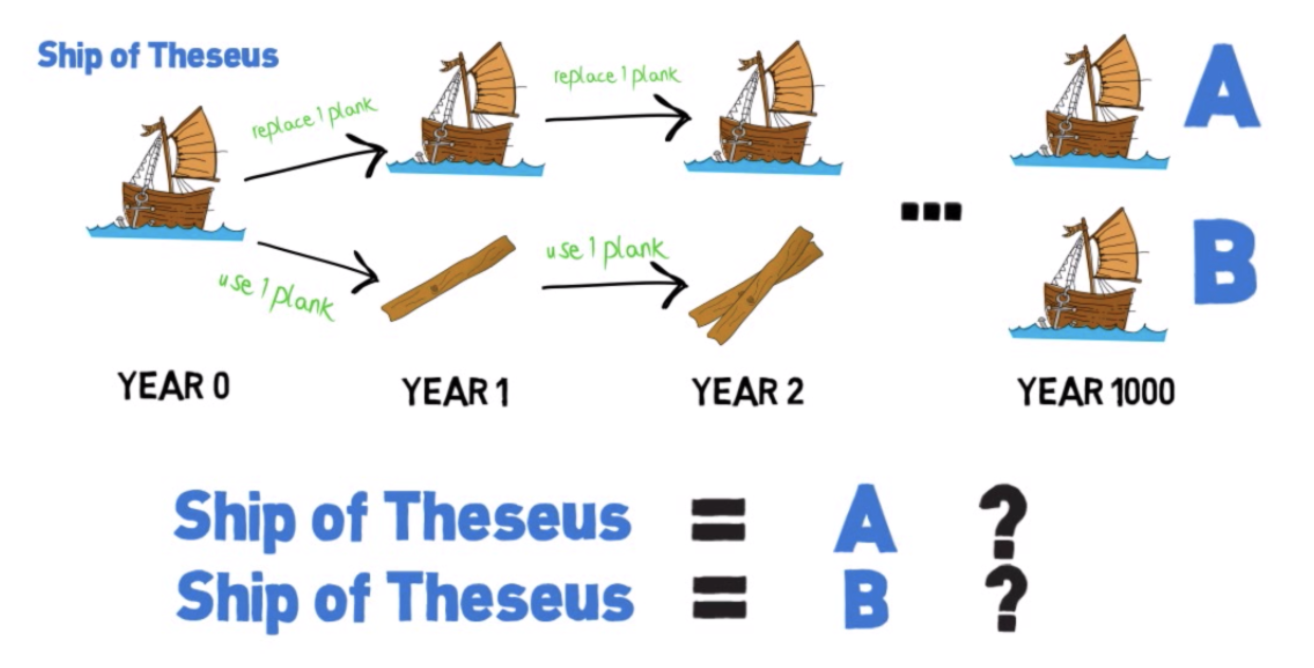
За годы ремонта в корабле не осталось ни одного атома вещества от первоначального корабля - материя уже другая, но идея, форма, скрепляющая эти атомы вместе всё та же. Множество мыслителей со времен античности и до наших дней спорили о том, можно ли считать корабль в таком случае тем же самым или нет. Сперва может показаться, что ответ прост - корабль тот же самый, ведь его идея осталась той же. Но тогда возникает другой вопрос: если бы старые доски сохранили и сколотили из них второй корабль, то какой из этих двух кораблей был бы настоящим и почему?
Сравнивая функциональное программирование с древнегреческой философией, можно сказать, что функции подобны бесплотным идеям, а данные подобны "твёрдой" материи. Мир - это поток преобразования материи через "формы" идей, а программа на LISP - это поток преобразования данных через вызов цепочки функций.
Похожее соответствие обнаружили физики при исследовании законов микромира. В своем поведении элементарные частицы проявляют удивительное свойство корпускулярно-волнового дуализма. Пока какое-либо состояние элементарной частицы, например её положение в пространстве, не измерено, его изменение носит вероятностный характер, однако эта вероятность строго подчиняется волновому уравнению Шрёдингера. Когда же это состояние подвергается измерению, то результат измерения показывает одно, выбранное абсолютно случайным образом из вероятных, значение данного состояния.
Получается, что пока состояние не измерено, мы рассматриваем элементарную частицу как бесплотную идеальную волну вероятности, а когда оно измеряется, то мы рассматриваем её в определенном моменте времени как "твёрдую" материальную частицу-корпускулу с определенным значением этого состояния. Другими словами, волновое уравнение Шредингера - это функция, существующая в мире математических идей с встроенным рандомом, а частица - это данные полученные при вызове этой функции Шрёдингера. Волна из мира идей отбрасывает тень на материальный мир в виде частицы.
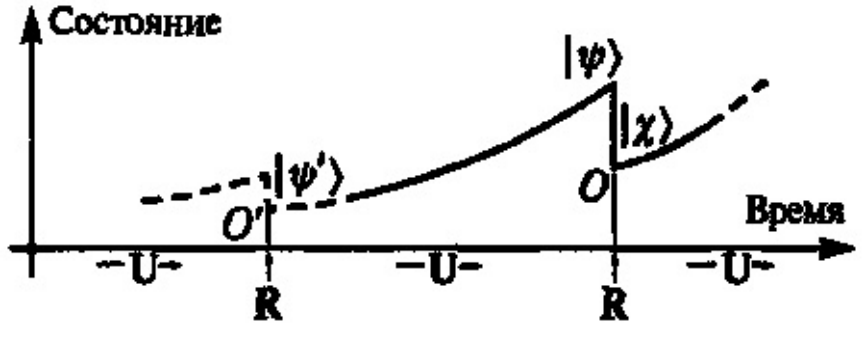
унитарная эволюция U (в соответствии с уравнением
Шредингера), перемежаемая с разрывной редукцией R вектора
состояния. Иллюстрация из книги Роджера Пенроуза "Новый ум короля".
Бесплотные идеи в философии Аристотеля придают форму материи, бесплотные волны в квантовой механике задают вероятность обнаружения определенного состояния частицы при измерении, а бесплотные функции в программировании преобразуют данные. Из этого так и тянет сделать вывод, что этот дуализм духа и плоти во Вселенной фундаментален. Однако это не совсем так. Восточные философские учения, такие как буддизм и адвайта-веданта, учат тому, что мир по своей природе не двойственен, а кажущиеся противоположности иллюзорны. Мы можем убедиться в этом сами, попробовав разбить на части пирамиду абстракций, которую мы называем материей.
Рассмотрим какой-нибудь материальный предмет: например, яблоко. Яблоко - это существующая исключительно у нас в уме абстракция совокупности различных его частей - кожуры, мякоти, семян, кусочка веточки. Каждая часть яблока в свою очередь - это абстракция над совокупностью клеток и происходящих между ними биологических процессов. Каждая клетка в свою очередь - это абстракция над совокупностью молекул различных соединений и происходящих между ними химических процессов. Молекула в свою очередь - это абстракция над совокупностью атомов и происходящих между ними физических процессов. Атом в свою очередь - это абстракция над совокупностью элементарных частиц и происходящих между ними квантовомеханических процессов. Можно ли считать элементарные частицы базовыми твёрдыми "кирпичиками" Вселенной?
Тщательное исследование поведения элементарных частиц в начале и середине XX века показало, что представление об элементарных частицах как о микроскопических "шариках" совершенно неверно. Например, частицы не имеют определенного положения в пространстве, а скорее имеют вероятность оказаться в какой-то точке пространства - положение в пространстве становится фактом только в момент измерения в конкретный момент времени, а после измерения положение опять становится вероятностным. Кроме того, принципиально невозможно одновременно измерить в один момент времени положение частицы в пространстве и её скорость.
Модель атома в виде точечных частиц, вращающихся по орбитам вокруг ядра в центре тоже оказалась неверной. Вместо этого оказалось, что электроны в атоме представляют собой скорее вероятностное облако вокруг ядра. Американский физик Роберт Оппенгеймер так описывал поведение электрона в атоме:
Если спросят, постоянно ли его положение, нужно сказать "нет", если спросят, меняется ли оно со временем, нужно сказать "нет". Если спросят, неподвижен ли он, нужно сказать "нет", если спросят, движется ли он, нужно сказать "нет"
Также оказалось, что мы не можем ничего сказать об элементарной частице, кроме числовых значений нескольких характеристик, проявляющих себя при её взаимодействии с другими частицами: массы, заряда, спина и нескольких других. Получается, что элементарная частица - это просто математическая абстракция, описывающая временной срез некоторого физического процесса.
При близком рассмотрении материя не просто "склеена" идеями, она, оказывается, буквально "соткана" из них. Наш мир - не тень мира идей, наш мир - буквально и есть мир идей. И точно так же, как при рассмотрении материи мы обнаруживаем, что она состоит из идей, американский математик Алонзо Чёрч при рассмотрении различных типов данных обнаружил, что они состоят из функций. Это великое открытие показало, что на фундаментальном уровне нет никакого разделения: ни между идеями и материей, ни между волнами и частицами, ни между данными и функциями. Всё это - разные проявления одного и того же.
Лямбда
Алонзо Чёрч разработал минималистичную формальную систему для записи математических функций под названием "лямбда-исчисление", названного так в честь использующейся в ней греческой буквы "лямбда". В лямбда-исчислении существует всего две операции: абстракция и аппликация. Абстракция, обозначающаяся той самой лямбдой - это объявление функции, а аппликация - это применение функции к некоторым параметром.
Функция y=x+1 в лямбда-исчислении будет записана в виде абстракции как:
y = λx.x+1Применение этой функции к числу два будет записано в виде аппликации как:
z = y 2Однако, по причине привычности большинства из нас к совершенно другой нотации объявления и аппликации функций в этом посте для удобства я буду использовать JavaScript-нотацию лямбда-функций.
Функция y=x+1 в JavaScript-нотации будет записана в виде абстракции как:
y = (x) => x + 1Применение этой функции к числу два будет записано в виде аппликации как:
z = y(2)Исследуя возможности лямбда-исчисления, Чёрч обнаружил, что с помощью одних только операций абстракции и аппликации можно выразить программу любой сложности, оперирующую любыми типами данных. Для этого Чёрч представил все типы данных в виде функций - позже такое представление стало именоваться кодированием Чёрча.
Рассмотрим для начала логику.
Булев тип данных, истину и ложь, можно представить в виде функций таким образом:
true = (x, y) => x
false = (x, y) => yПосле мы можем определить в виде функций базовые логические операции:
and = (p, q) => p(q, p)
or = (p, q) => p(p, q)
not = (p) => (x, y) => p(y, x)
if = (p, x, y) => p(x, y)Посмотрим как работает получившаяся система:
result1 = and(true, false)
// подставляем значения true и false в виде функций
result1 = and((x, y) => x, (x, y) => y)
// подставляем параметры в значение and в виде функции
result1 = ((x, y) => x)((x, y) => y, (x, y) => x)
// применяемая функция возвращает первый параметр, то есть
result1 = (x, y) => y
// сравнив эту функцию с нашими двумя логическими значениями, мы понимаем, что
result1 = falseresult2 = or(true, false)
// подставляем значения true и false в виде функций
result2 = or((x, y) => x, (x, y) => y)
// подставляем параметры в значение or в виде функции
result2 = ((x, y) => x)((x, y) => x, (x, y) => y)
// применяемая функция возвращает первый параметр, то есть
result2 = (x, y) => x
// сравнив эту функцию с нашими двумя логическими значениями, мы понимаем, что
result2 = trueresult3 = not(true)
// подставляем значение true в виде функции
result3 = not((x, y) => x)
// подставляем параметры в значение not в виде функции
result3 = (x, y) => ((x, y) => x)(y, x)
// применяемая функция возвращает первый параметр, то есть
result3 = (x, y) => y
// сравнив эту функцию с нашими двумя логическими значениями, мы понимаем, что
result3 = falseresult4 = if(false, 1, 2)
// подставляем значение false в виде функции
result4 = if((x, y) => y, 1, 2)
// подставляем параметры в значение if в виде функции
result4 = ((x, y) => y)(1, 2)
// применяемая функция возвращает второй параметр, то есть
result4 = 2Используя арифметику Пеано, можно выразить с помощью функций даже числа. Для этого нужно задать две базовые функции:
0 = (f, x) => x
next = (n) => (f, x) => f(n(f, x))После этого мы можем выразить все числа через эти две функции:
0 = (f, x) => x
1 = (f, x) => f(x)
2 = (f, x) => f(f(x))
3 = (f, x) => f(f(f(x)))
...Точно так же можно определить и арифметические операции:
plus = (m, n) => (f, x) => m(f, n(f, x))
multiply = (m, n) => (f, x) => m(n(f), x)Посмотрим как работает получившаяся система:
result5 = plus(1, 2)
// подставляем значения 1 и 2 в виде функций
result5 = plus((f, x) => f(x), (f, x) => f(f(x)))
// подставляем параметры в значение plus в виде функции
result5 = (f, x) => ((f, x) => f(x))(f, ((f, x) => f(f(x)))(f, x))
// упрощаем выражение
result5 = ((f, x) => f(x))(f, f(f(x)))
// упрощаем выражение еще раз
result5 = f(f(f(x)))
// сравнив эту функцию с нашими числами, мы понимаем, что
result5 = 3Подобным образом любые типы данных, включая даже строки и списки, можно определить через функции. Ещё более удивительно то, что эту систему можно упростить, выразив все возможные функции в виде комбинации всего трёх элементарных функций. Занимающаяся этим область математики под названием комбинаторная логика была разработана российским математиком Моисем Исаевичем Шейнфинкелем и развита американским математиком Хаскеллем Карри. В честь последнего был назван один из самых известных функциональных языков программирования Haskell и операция каррирования.
Комбинаторная логика позволяет выразить любую функцию в виде бинарного дерева, узлы которого представляют из себя одну из трёх функций, называющихся комбинаторами:
I = (x) => x
K = (x, y) => x
S = (x, y, z) => x(z, y(z))Названия I, K, S означают identity (тождество), konstant (постоянная) и substitution (подмена) соответственно. Попробуем свести к SKI-исчислению булеву логику, описанную нами выше в виде лямбда-исчисления:
true = K
true = (x, y) => x
false = S(K)
false = (x, y) => K(y, x(y))
false = (x, y) => yПосле мы можем определить через SKI-комбинаторы логические операции.
Логическое "и" определяется в виде передачи в функцию истины/лжи false последним параметром:
and = false
true(true, and) = true(true, false) = K(true, false) = true
true(false, and) = true(false, false) = K(false, false) = false
false(true, and) = false(true, false) = K(false, true(false)) = false
false(false,and) = false(false, false) = K(false, false(false)) = falseЛогическое "или" определяется в виде передачи в функцию истины/лжи true первым параметром:
or = true
true(or, true) = true(true, true) = K(true, true) = true
true(or, false) = true(true, false) = K(true, false) = true
false(or, true) = false(true, true) = K(true, true(true)) = true
false(or, false) = false(true, false) = K(false, true(false)) = falseЛогическое "не" определяется в виде передачи в функцию истины/лжи параметров false, true:
true(false, true) = K(false, true) = false
false(false, true) = K(true, false(true)) = trueТочно так же с помощью SKI-комбинаторов можно выразить и все остальные типы данных, представленные в виде кодирования Чёрча, но к сожалению описание этих операций выходит далеко за пределы этого поста.
Йота
В начале было Слово, и Слово было с Богом, и Слово было Бог
Евангелие от Иоанна
Согласно этой известной строке из евангелия, Господь сотворил мир, окликнув его из небытия своим словом. Что же это было за слово, обладающее могуществом породить целую Вселенную?
В еврейской Торе создатель мира упоминается под множеством различных имён, но только одно из них считается его личным именем, а не титулом. Это имя записывается как יהוה, но обычно не читается, так как согласно традициям евреи должны соблюдать одну из основных заповедей - "не упоминай имени моего всуе". Точное произношение этого имени, известного как тетраграмматон, утеряно в веках, но обычно в западной традиции его произносят как Яхвэ или Иехова/Иегова. Слово יהוה объединяет в себе три времени глагола "быть", его можно перевести как "был, есть и будет".
Первая буква личного имени Бога י в еврейском и родственном ему финикийском алфавите называется "йуд". В греческом алфавите, перенятом древними греками с некоторыми усовершенствованиями у финикийцев, соответствующая буква носит название "йота". Йуд и йота записываются в виде коротенького штриха - это самые маленькие буквы в письменных алфавитах греков и евреев, обозначающие самый короткий звук "й".
Именно из-за своего малого размера буква "йота" была выбрана американским лингвистом Крисом Баркером для обозначения самого минимального из возможных комбинаторов - универсального йота-комбинатора, с помощью которого можно выразить I, K и S-комбинаторы, а соответственно и все возможные функции.
Для начала выразим функцию I через S и K:
// Первый вариант
I = S(K, K)
I = (x) => K(x, K(x))
I = (x) => x
// Второй вариант
I = S(S, K, K)
I = S(K, K(K))
I = S(K, K)
I = x => K(x, K(x))
I = x => K(x, x)
I = x => xПосле введем оператор ι и выразим его через S и K:
ι = (x) => x(S, K)При подстановке вместо S и K их полных значений получаем:
ι = (x) => x((a,b,c) => a(c, b(c)), (d, e) => d)Теперь мы можем выразить сами SKI-комбинаторы исключительно через йоту:
I = ι(ι)
K = ι(ι(I))
K = ι(ι(ι(ι)))
S = ι(ι(ι(I)))
S = ι(ι(ι(ι(ι))))Так как с помощью SKI-комбинаторов можно выразить любую возможную функцию, а сами комбинаторы можно выразить через йоту, то получается, что любую возможную функцию можно выразить через йоту. А значит йота - это то самое Слово, с помощью которого можно сотворить целую Вселенную. Господь в откровении Иоанна Богослова говорит "Я есмь Альфа и Омега", но разве не правильнее ли будет сказать "Я есмь Йота и Лямбда"?
В первой строке книги Бытия сказано:
В начале сотворил Бог небо и землю
Вероятно, на эту строку Библии сильно повлияла космогоническая литература аккадцев - родственного древним евреям семитского народа. Даже мифический первый еврей Авраам был родом из месопотамского города Ур, располагавшегося в междуречье Тигра и Ефрата и бывшего одним из центров шумеро-аккадской цивилизации.
В аккадском космогоническом мифе Энума Элиш говорится:
Когда наверху не названо небо, внизу земля именем не называлась
Эта строка проливает свет на значение первой строки книги Бытия. Получается, что Бог для сотворения мира своим Словом именует противоположности, тем самым отделяя бытие от небытия, жизнь от смерти, движение от покоя, единицу от нуля, материю от идей, частицу от волны, данные от функции. Особенная мистическая красота заключается в том, что в созданном на основе йота-исчисления языке программирования Iota любая программа тоже состоит из всего двух символов: нуля и единицы. Ноль кодирует открывающуюся скобку, а единица йоту.
Пример программы на языке Iota:
0011011При замене нуля на открывающуюся скобку, а единицы на йоту получаем:
((ιι(ιιЭто выражение аппликации с закрывающимися скобками записанное в лямбда-нотации выглядит следующим образом:
((ιι)(ιι))Во всей статье вместо лямбда-нотации я использовал более привычную большинству JavaScript-нотацию. В ней это выражение будет выглядеть так:
(ι(ι))(ι(ι))Йота - это тьюринг-полный язык, на котором можно написать программу любой сложности. Однако лучшие мыслители человечества всё ещё бьются над решением важного философского вопроса: "Но зачем?".
Вселенная как программа на LISP
У идеалистической философии Платона до сих пор много поклонников. Особенно много их среди математиков. Известно, что убежденным сторонником платонизма был великий немецкий логик Курт Гёдель. Среди наших же современников два самых известных платоника - это астрофизик Макс Тегмарк и математик-программист Стивен Вольфрам.
В своей книге "Наша математическая Вселенная" профессор Тегмарк излагает свои оригинальные взгляды на фундаментальные основы физики. Его картина мира исходит из того, что всё, что нам известно об элементарных частицах - это то, как эти частицы проявляют себя во взаимодействии с другими частицами и то, что их поведение подчиняется волновому уравнению Шрёдингера. Если зайти на Википедию в статьи про электрон и нейтрино, то можно увидеть, что всё чем отличаются эти частицы друг от друга - это числовые значения нескольких характеристик: массы, электрического заряда, цветового заряда, спина, лептонного и барионного чисел и нескольких других. Тегмарк утверждает, что мы можем придумать для себя любые словесные описания физических процессов, но в конце концов всё наше представление о них сводится к одному - числам и формулам. А раз ничего другого кроме формул и чисел мы о Вселенной содержательно сказать не можем, то стоит заключить, что наша Вселенная - это просто огромная математическая структура.
Мысли Тегмарка развил и дополнил создатель пакета Mathematica программист Стивен Вольфрам. По его мнению, мир представляет из себя не просто математическую структуру, а скорее циклический процесс вычисления преобразований математической структуры по некоторому простому правилу. Пользуясь религиозной метафорой, можно сказать, что с точки зрения Вольфрама Бог при сотворении Вселенной задал всего две вещи - начальное состояние некоего графа и правило, по которому этот граф изменяется.
Возможно, существует бесконечное количество комбинаций различных начальных состояний и правил, но только в некоторых из них возможно появление сложных структур и жизни. Примером такого простого правила с простыми начальными условиями, порождающими сложные структуры, может служить знаменитая игра "Жизнь" Джона Конвея.
Согласно размышлениям Вольфрама, наша Вселенная - это один гигантский бесплотный компьютер, который рекурсивно вычисляет все возможные программы, все возможные алгоритмы. А мы можем добавить, что запрограммирован этот компьютер, наверняка, на языке Бога - языке универсального йота-комбинатора, языке SKI-комбинаторов, языке лямбда-исчисления Чёрча, на LISP-е.
В этом посте я лишь вкратце коснулся взглядов Тегмарка и Вольфрама. Если вам интересно понять их концепции в деталях, то вы можете почитать серию моих предыдущих постов:
Комментарии (95)

softaria
30.10.2023 14:09+3PL1 же. Противоположная парадигма - попытка добавить в язык все известные средства выражения. Максимизация вместо минимизации.

Ru6aKa
30.10.2023 14:09+1Выбрал Perl, из-за принципа TMTOWTDI, это максимизация не количества конструкций языка, а вариантов записи решения с использованием конструкций языка.

rutexd
30.10.2023 14:09+12Функциональное программирование хорошо в одном лишь случае - когда этим не злоупотреблять и не строить вокруг этого центр вселенной, как пытаются делать многие фанаты-функциональщики.
Статья хорошая однако уже на первых примерах хорошо видно, почему функциональное программирование это не про код а про решение проблем самой функциональной парадигмы и игру с конструктом языка, чем решение прикладных проблем. Но это лишь мое имхо...

WebPeople
30.10.2023 14:09+5Если подумать, то это не так. Отталкиваясь от размышлений автора, можно прийти к тому, что для решения прикладных задач достаточно использовать абстракции верхнего уровня, предполагая под ними функцию, а не объект. Не обязательно все программировать используя базовый кирпичик (функцию, Слово, йоту). Это как программировать даже не на ассемблере, а на 1 и 0. Можно использовать абстракции верхнего уровня и спокойно писать код как привыкли, но держать в уме, что это все функции. И язык lisp помогает это делать проще, т.к. он изначально задумывался как функциональный. Но нам ведь ничего не мешает применять это в разработке и на других языках. Это как в питоне - все есть объект. Мысленно подменяем объект на функцию, и спокойной решаем поставленную задачу. Кстати, мышление в той парадигме, что все есть функция, помогает проще решать сложные задачи, типа компьютерного зрения или разработки ИИ.
Статья потрясающая, закинул себе в закладки, чтобы иногда перечитывать!

Alonerover
30.10.2023 14:09+1Не обязательно все программировать используя базовый кирпичик (функцию, Слово, йоту). Это как программировать даже не на ассемблере, а на 1 и 0.
Жаль лайкнуть не имею возможности вашу мысль, но развить её стоит - крайняя форма такого программирования описана у Павла Шумилова "Иди, поймай свою звезду":
"Знаешь анекдот, как программист кипятит чайник. Дано: пустой чайник, кран, спички, газовая плита. Программа действий: наполнить чайник водой из-под крана, поставить на плиту, зажечь газ. Ждать, пока закипит чайник. Эта программа оформляется как объект. Второй случай. Все то же самое, но чайник с водой уже стоит на плите. Действия программиста: вылить воду из чайника и выполнить предыдущий объект.
Грустно. А нырнуть внутрь объекта нельзя? Туда, где надо газ зажечь?
Нельзя. Можно добавить новое свойство или действие. В нашем случае - воду вылить. Будет новый объект. Но внутрь влезть нельзя. Объект дается как единое целое. Никто не знает, что там внутри. Все давно забыли, откуда ноги растут. В результате получается колоссальное дублирование кода и данных и огромная потеря производительности компьютера. С каждым годом компьютеры требуют все больше памяти, а работают все медленнее."

CTheo
30.10.2023 14:09Было бы хррошо, если бы эта проблема решалась самим компьютером. Установил программу, а она анализируется на предмет паттернов, возможно на уровне машинного кода. Как link time optimization, только не ограничено одним языком внутри одной компиляции.

Keeper10
30.10.2023 14:09Так это же старый анекдот про математика и физика.
Математику и физику была предложена одна и та же задача: вскипятить чайник. Даны подсобные инструменты: плита, чайник, водопроводный кран с водой, спички. Оба поочередно наливают воду в чайник, включают газ, зажигают его и ставят чайник на огонь.
Затем задачу упростили: предложен чайник, наполненный водой и плита с горящим газом. Цель та же — вскипятить воду. Физик ставит чайник на огонь. Математик выливает из чайника воду, выключает газ и говорит: "Задача свелась к предыдущей."

yaxn
30.10.2023 14:09Так одно другому не противоречит. Прикладное программирование есть то самое вытачивание неидеальных кругов на станке. Статья посвящена высшей абстракции, которая, так совпало, называется тем же словом.

nikis05
30.10.2023 14:09+11Я всегда люблю приводить пример «заказ пиццы» и «рецепт пирога». Когда мы заказываем пиццу, мы используем декларативный стиль - мы не пишем для пиццерии пошаговую инструкцию, что делать, а лишь указываем, какую пиццу мы хотим получить, в каком количестве, где и когда. Это просто и удобно.
С другой стороны, когда мы пишем рецепт пирога, мы используем императивный стиль:
1. Возьмите белки от двух яиц 2. Смешайте с молоком и мукой в определенной пропорции 3. … N. поместите в духовкуЕсли бы рецепт выглядел как «выньте из духовки помещенную туда час назад при температуре 210 градусов тщательно перемешанную и без комочков смесь молока, муки и белков от двух яиц», это был бы ужасный рецепт.
Иногда две парадигмы могут совмещаться при решении одной задачи - например, мы заказываем пиццу, а курьеру пишем пошаговую инструкцию, как найти нашу квартиру. Никому в голову не приходит везде использовать только одну парадигму и фанатично отстаивать ее превосходство - под разные ситуации лучше подходят разные способы доносить информацию. Почему же в написании кода должно быть по-другому?

tnc4401
30.10.2023 14:09+5Вот так намного проще? выньте из духовки - помещенную туда час назад при температуре 210 градусов - смесь тщательно перемешанную и без комочков - молока муки белков - от двух яиц
tnc4401
30.10.2023 14:09+2И даже так

Одно и то же дерево из "функционального рецепта по приготовлению пирога".
Просто отрисованное в другую сторону. Кажется что левое функциональное дерево читается также как императивный рецепт. И особой разницы нет.
Но функциональный редактор потребует скобочек как в lisp / отступов как в питоне/ дерева или какого-то другого оформления.

Wizard_of_light
30.10.2023 14:09+5выньте из духовки - помещенную туда час назад"Залейте компоненты в колбу и хорошенько перемешайте. Только осторожно, иначе может взорваться"

tnc4401
30.10.2023 14:09выньте из духовки - помещенную туда час назад - вполне норм. Ведь исполнение идет изнутри. Сначала запечь на 1 час, а потом вынуть. При такой последовательности как в лиспах ничего не взрывается.
Это эзотерический пример. Может надо даже так- вынуть (через час) - запекать (210 градусов)В случае же компонентов в колбе пишем
- перемешать (осторожно, содержимое) - залить (осторожно, компоненты)А вот эта инструкция очень странная:
"Залейте компоненты в колбу и хорошенько перемешайте. Только осторожно, иначе может взорваться" и будет, как я понимаю такой ????- следить и делать осторожно - перемешать хорошо - залить компоненты
Wizard_of_light
30.10.2023 14:09Ну, изначально это был анекдот про инструкцию в химической лаборатории :) Я это к тому, что программировать можно "от результата", но машине всё равно придётся считать "от исходных". В идеале это учитывает среда программирования, но это в идеале.

Gryphon88
30.10.2023 14:09+2Нинада. Люди плохо думают в обратной польской нотации или AST-деревьями.

sundmoon
30.10.2023 14:09+1Разработчики инструментов это та элита, которая обязана думать хорошо за простых смертных программистов - которые в результате свободны управлять машинами так, как удобно людям.

Gryphon88
30.10.2023 14:09+4Проблема в том, что когда разработчики инструментов начинают чувствовать себя элитой, пользователи этих инструментов начинают страдать.

GBR-613
30.10.2023 14:09+4У компьютера и у человека голова по разному работает. Для компьютера это рецепт как рецепт, а вот человеку, чтобы такие рецепты писать и читать, надо делать огромное усилие. Поэтому LISP по своему прекрасен, но пользоваться им хотят только тонкие ценители красоты, а широкие народные массы - не хотят (и вряд-ли захотят в будущем).

Voliker
30.10.2023 14:09Ну, все-таки надо подметить что на "самом низком" уровне машинных инструкций компьютера все-таки скорее сугубо декларативны. Функциональные языки на этом фоне для значительной части компьютеров выглядят более чуждыми чем декларативные.

SergioShpadi Автор
30.10.2023 14:09+3Были компьютерные архитектуры специально для лиспа: https://ru.m.wikipedia.org/wiki/Лисп-машина

Voliker
30.10.2023 14:09+1Да, поэтому я обмолвился про "значительную часть" :)
Лисп-машины это скорее исключение из правил в мире победившего ARM и x86

gatoazul
30.10.2023 14:09+5Лисп - отличный прикладной язык, куда за время его существования запихали множество разных идей, в том числе из других языков. А многие в рамках лисп-культуры и придумали, откуда они разошлись по другим языкам.
И никакой он не строго функциональный, а мультипарадигменный. Есть там и императивная часть, и ООП (причем куда более навороченный, чем в том же С++). А уж в плане генерации кода - это мать всех прочих языков.
Я рекомендую вам с ним ознакомиться. Писать на нем вы вряд ли станете, но полезного можно утащить немало.
А вот описания, подобные этой статье, создают совершенно ложное впечатление, будто это нечто эзотерическое и доступное только жрецам.

GBR-613
30.10.2023 14:09+2Я учил Common Lisp в начале 90-х, и тогда там не было ни императивной части, ни ООП (хотя упоминалось, что есть диалекты с ООП).

gatoazul
30.10.2023 14:09+1Присваивания и do в Лиспе если не с первой версии, то с 1.5 точно. А в Коммон Лиспе еще и обобщенная функция присваивания setf, и навороченный loop.

CTheo
30.10.2023 14:09+1Как мне кажется, тут дело в том, что обычно императивные алгоритмы явно описывают переходы между состояниями, в духе Хоаровой логики (было-действие-стало). А декларативно обычно описывают отдельное состояние "в вакууме". Декларативное приходится переводить как-то в императивное, например, для двух данных декларативных состояний вычислить необходимые действия.

DirectoriX
30.10.2023 14:09мы не пишем для пиццерии пошаговую инструкцию, что делать, а лишь указываем, какую пиццу мы хотим получить
Но ведь рецепт не нужно писать заказчику только потому, что в самой пиццерии уже есть жёстко забитый список императивных рецептов. А вот если вы хотите заказать пиццу "как мой коллега привозил на работу на дни рождения" - вам придётся явно указывать набор ингредиентов... если ваша пиццерия вообще позволяет менять состав.
Впрочем, с функциональными языками (особенно с теми, которые чистые) так и есть - как только доходит до деталей выполнения, то обязательно нужна прослойка-рантайм этих самых "рецептов", а то и железо у нас императивно-пошаговое, и сайд-эффекты нужны (хотя бы ввод-вывод), и ресурсы мало того, что не бесконечные, так ещё их явно запрашивать у ОС надо...

h1p3r
30.10.2023 14:09-1Ну с числами, разобрались. А с символами? Автор, а можете теперь данные о положении символов в тексте и в таблице символов ужать до функции одной. Скажем, что-то по типу множества мандельброта. А затем несколько тысяч итераций пропускать тексты в нейросеть, модифицируя эту функцию (для каждого символа/знака) и потом попробовать заставить нейросеть продолжать фразу?

Vpan
30.10.2023 14:09+2Не все числа можно представить как результат функции. Есть трансцедентные числа, они не выразимы с помощью многочлена (как я понял, функции); они не счётны, в отличие от алгебраических (выразимых с помощью многочленов), то есть для них невозможна операция в духе "получить следующее число применением функции next к уже имеющемуся числу"

neyronon
30.10.2023 14:09+2Тут речь не о многочленах. Трансцендентные числа тоже вычислимы в большинстве своем. Например пи и е можно выразить через тригонометрические функции.

flx0
30.10.2023 14:09+2Трансцендентные числа тоже вычислимы в большинстве своем.
В меньшинстве. Рандомно выбранное действительное число невычислимо с вероятностью 100%. Просто потому что множество алгоритмов счетное.
Другое дело, что невычислимые числа и трансцендентные - это разные сущности. Среди трансцендентых чисел есть вычислимые.

ksbes
30.10.2023 14:09+2Вообще практические вычисления, особенно вычисления на компьютере имеют дело только с даже не целыми числами, а натуральными + ноль. Все другие числа полюбому как-то моделируются с помощью них (ноль минус пять, два разделить на три, шесть поюс 4 корня квадратных из минус единицы ...).
Поэтому вычислить точно даже 1/7 вы не можете, не то что пи! ( вспоминаем проблему с 3 * 0.(3) )Но зато в функциональную парадигму всё ложится замечательно! 1+2 - полностью взаимозаменяемо с 3. А значит и 13/17 - полностью взаимозаменяемо с "истинным" значением результата этой операции деления. С пи - алгоритм "получения" поабстрактнее и посложнее, но принцип тот же.

Vpan
30.10.2023 14:09-113/17 это рациональное число, его можно выразить как выход функции деления, на вход которой подали числа 13 и 17 и поэтому оно ложится в концепцию функционального программирования. Число Пи - другое, его нельзя выразить как результат какой-то функции, я не знаю, как оно ложится в концепцию функционального программирования.

ksbes
30.10.2023 14:09-1Алгоритм получения числа Пи: измеряем длину окружности, измеряем диаметр, делим.
Понятие "измерение" - оно, конечно, внешнее по отношению к математике.
НО. Нет никаких других способов (ну кроме как выдумать) получить исходные числа для математических вычислений.
В концепции функционального программирования любое исходное, заданное число - это и есть подобный "внешний алгоритм" (число и способ его получения - взаимозаменяемы, даже если способ получения - "нематематический").
В функциональном подходе числа являются как бы API математики к внешнему миру. Заданные в теле программы константы или полученные с внешних датчиков 0, 1 или 3454,7(647) тоже не являются результатом какой-то функции.
Однако т.к. это именно числа - то эти "внешние алгоритмы" можно комбинировать так же как и числа с помощью различных функций и получать полезный выхлоп. В этом весь смысл, как я понимаю.
Keeper10
30.10.2023 14:09+2Число пи можно вычислить и чисто алгоритмически, с любой заранее заданной точностью. Берём бесконечный ряд Лейбница (например) и считаем, пока не будет достигнута нужная погрешность.

Vpan
30.10.2023 14:09-1Ну так просто получить число Пи не выйдет: допустим измерили диаметр, он оказался равен 10 попугаям, измерить длину окружности в тех же попугаях не выйдет, нужно будет измерять в мартышках, допустим 5 мартышек. Как разделить 5 мартышек на 10 попугаев непонятно, они несоизмеримы.

vadimr
30.10.2023 14:09-1Просто потому что множество алгоритмов счетное.
Тут тонкое дело, упирающееся в то, как мы определим понятие алгоритма. Если алгоритм определить как последовательность шагов для получения результата, то множество алгоритмов счётно. Но алгоритм можно определить просто как способ получения результата, и тогда множество алгоритмов может быть любым.

ksbes
30.10.2023 14:09Множество алгоритмов с конечным числом шагов по любому счётно. А вот если мы возьмём и алгоритмы с бесконечным числом (прописанных) шагов - то тогда континуально.
А насчёт определения: в течении тысячелетий под алгоритмом понимали только порядок выполнения расчётов (алгоритм - это всё тот же аль-Хорезме (aka "алгебра"), только искажённый по другому). Ну там деление в столбик, вычисление логарифма на счётах. И теорию таких алгоритмов хорошо развили и проработали в середине 20-го века Тьюринг и другие.
Но связи с развитием футуризма и появления идеи робота понятие алгоритма поползло в реальную жизнь. Алгоритмами начали называть и кулинарные рецепты и прочую нематематическую хрень. Это очень существенное расширение понятия.И я как-то не знаю серьёзных попыток научно проработать теорию таких расширенных алгоритмов (разве что ТАУ - но это не про алгоритмы). Просто тупо расширять машину Тьюринга будет некорректно.
vadimr
30.10.2023 14:09+1Никто не обещал, что алгоритм состоит из шагов. Аналоговая вычислительная машина, например, работает по-другому.
А что касается Тьюринга, то он позднюю часть своей научной карьеры посвятил алгоритмам супервычислений, где действует оракул, принципиально не сводимый к последовательности шагов.
Популярное понимание вопроса застыло примерно на уровне аспирантских лет Тьюринга.

ksbes
30.10.2023 14:09Никто не обещал, что алгоритм состоит из шагов.
Ну как минимум Википедия обещает. Там везде "set/sequence/step-by-step".А вот большевики - действительно явно не обещали (хотя и подразумевают). Кому верить? ¯_(ツ)_/¯

vadimr
30.10.2023 14:09Википедии верить вообще нельзя. Но в вопросе определений, собственно, неважно, кому верить, а важно условиться о терминах.

nikis05
30.10.2023 14:09+9«Дорогой, мой отец - энтерпрайз Java разработчик, давай без разговоров про LISP и Haskell за столом»
Я после одной рюмки:

Suseika
30.10.2023 14:09Отличный язык для написания бизнес-логики, со вводом-выводом из окружения в нём как работать?

demimurych
30.10.2023 14:09Никак. И єто то самое место, где дружит императивная парадигма с функциональной.

neyronon
30.10.2023 14:09+10Чувствовал, что большинство выберет в качестве языка дьявола JS. Но как поклонник С++ я искренне убежден, что это именно он.

ksbes
30.10.2023 14:09+1Причём всегда, независимо от сравнения. Это просто язык дьявола - по определению! Эталон.

Serge78rus
30.10.2023 14:09+2Тогда уж скорее это C. В C++ прямое обращение к дьяволу осложняется более строгой типизацией.

DEugene
30.10.2023 14:09+5А раз ничего другого кроме формул и чисел мы о Вселенной содержательно сказать не можем, то стоит заключить, что наша Вселенная - это просто огромная математическая структура.
Не, не стоит так заключать. То что мы можем содержательно только на уровне формул и чисел сказать о вселенной, говорит лишь о том что наши инструменты для выражения и познания вселенной имеют ограничения физиологического характека. Формулы и числа - конструкт символьной системы мышления, как способа интерпретации сигналов человеческой сенсорики, за пределы которой не выпрыгнешь, можно только расширять сенсорику техническими средствами, и все равно результаты перегонять в область символьного восприятия человека - теряя информацию по пути.

Wizard_of_light
30.10.2023 14:09+3Я бы не абсолютизировал математику и функции как "основу мироздания" - потому что как минимум половина нашей математики говорит о человеке, а не о мироздании. 1+1=2 нам кажется элементарным, потому что мы можем взять один камешек и другой камешек, и убедится, что теперь у нас два камешка, и соседу показать, а 4-тензор кажется сложным потому что для его понимания и объяснения придётся подтягивать математический аппарат, шлифовавшийся столетиями. Идеальные геометрические фигуры - это не столько чудо природы, сколько апогей ленивых вычислений, они идеальны по соотношению "цена/качество" для нашего мозга, позволяют выкинуть максимум информации о геометрии реальных объектов и всё ещё полезно оперировать ими в воображении.

MasterMentor
30.10.2023 14:09+3Почти под каждым моим постом на Хабре восхищенные читатели пишут мне доброжелательные комментарии вроде этого:
Автору с таким перепутанным мировоззрением светит только психиатрическая палата или монастырь (первое предпочтительнее — там есть лечение и хоть какие‑то перспективы).
Наивно полагать, что мягкие стены остановят полет мысли, ведь управлять Вселенной можно и оттуда.
(с) SergioShpadi, Как управлять Вселенной, не покидая психиатрической лечебницы
Видимо, продолжаете цикл статей.

vadimr
30.10.2023 14:09Очень режут глаз присваивания в разговоре о функциональном программировании и тем более о лямбда-исчислении.

mayorovp
30.10.2023 14:09+1А где там присваивания?

vadimr
30.10.2023 14:09А как ещё понимать знаки равенства в статье?
Как вообще вы интерпретируете запись:
y = λx.x+1?

mayorovp
30.10.2023 14:09+1"y равна по определению λx.x+1"
Или, что то же самое, "определим y как λx.x+1"

vadimr
30.10.2023 14:09Давайте не так быстро. x – это связанный терм в инфиксно записанном лямбда-выражении справа, включающем также свободный терм 1. А что такое вообще здесь y?

mayorovp
30.10.2023 14:09+3Псевдоним для терма λx.x+1

vadimr
30.10.2023 14:09Ну назовите определением псевдонима, а не присваиванием, разницы нет. Это не лямбда-исчисление тогда. Лямбда-исчисление основано на бета-редукции, то есть на чисто формальном преобразовании цепочки символов, которое теряет свою применимость при таком переобозначении.
Никакой внутренней семантики вычислительного процесса, отличной от эквивалентного синтаксического преобразования цепочки символов, составляющей лямбда-выражение, в лямбда-исчислении нет.
Результат редукции лямбда-выражения полностью содержится в его записи.

mayorovp
30.10.2023 14:09+3Разница есть, и принципиальная. Присваивание происходит в рантайме, а определение - всего лишь часть синтаксиса языка. Иными словами, присваивание - это связывание переменной и значения, а определение - это связывание имени и терма.
Лямбда-исчисление основано на бета-редукции, то есть на чисто формальном преобразовании цепочки символов, которое теряет свою применимость при таком переобозначении.
Попробуйте найти хоть одну нетривиальную математическую работу по лямбда-исчислению, в которой ни разу не был бы объявлен псевдоним. А потом объясните, почему в математических работах псевдонимы допускаются, а в программировании они недопустимы.

vadimr
30.10.2023 14:09-1Присваивание происходит в рантайме
Совершенно не обязательно, но допустим.
Иными словами, присваивание - это связывание переменной и значения, а определение - это связывание имени и терма.
В контексте разговора о языке Лисп от меня ускользает, чем одно связывание слота атома со списком отличается от другого.
А потом объясните, почему в математических работах псевдонимы допускаются, а в программировании они недопустимы.
Они допустимы в программировании, как всякий синтаксический сахар. И даже функция setq в Лиспе существует. Но они не являются частью концепции функционального программирования, и не на их основе было бы разумно объяснять основы.

mayorovp
30.10.2023 14:09В контексте Лиспа я тоже не понимаю чем они отличаются и почему вообще Лисп считают функциональным языком.
Однако, запись
y = λx.x+1совершенно точно не является частью программы на языке LISP.Но они не являются частью концепции функционального программирования, и не на их основе было бы разумно объяснять основы.
Возможность определить псевдоним для терма является базовой "фичей" математики, и было бы неразумно ей не пользоваться при объяснении чего бы то ни было.

vadimr
30.10.2023 14:09Однако, запись
y = λx.x+1совершенно точно не является частью программы на языке LISP.Вопрос в том, частью чего она является.
Возможность определить псевдоним для терма является базовой "фичей" математики, и было бы неразумно ей не пользоваться при объяснении чего бы то ни было.
Ага, а потом Бурбакам приходится за эти псевдонимы отдуваться сотнями страниц аксиоматических определений (кстати, бурбакизм очень идейно близок к функциональному программированию).

mayorovp
30.10.2023 14:09+2Вопрос в том, частью чего она является.
Это математическая нотация, повсеместно используемая в лямбда-исчислении. Языков программирования с именно таким синтаксисом я не знаю (возможно, какая-нибудь Agda и "прожуёт" эту формулу).
Ага, а потом Бурбакам приходится за эти псевдонимы отдуваться сотнями страниц аксиоматических определений
Возможность введения псевдонимов является частью мета-языка математики, она не определяется аксиомами на уровне математической теории.
Даже Бурбаки вынужденно использовали псевдонимы, ведь в противном случае даже определение единицы у них бы заняло 2 409 875 496 393 137 300 000 000 000 000 000 000 000 000 000 000 000 000 знаков (сам я не проверял, информация из Википедии).

ksbes
30.10.2023 14:09-2Вообще в математике "=" - это не присваивание, а оператор сравнения. Если я правильно помню. Математика оперирует логическими выражениями вида "если значения y и x + 1 совпадают, то совпадут и значения y-1 и х"
Так что его употребление в математике вполне оправданно. В частности выражение y = λx.x+1 можно читать как: "Если неизвестное лямбда выражение y совпадает с λx.x+1, то ... (дальнейшие рассуждения)".
В чём проблема?

MasterMentor
30.10.2023 14:09+1Ой, а можно я отвечу?
В 1930-х чувак придумывал кодировщикам спецификацию записи математических функций для первых ЦВМ. На Liste - то есть листе обычной белой бумаги (не путать с Lisпом), функции пишут, вроде как:
f(x,y,z) = x+y+z
Вот он долго не думая и записал: "Повелеваю, функции записывать так: (место для имени функции) = λ (место для перечня аргументов функции) . (место для тела функции)" и нарёк сё "абстракция". А вызов функции с аргументами - привет(в,е,н,я) - он нарёк "аппликация". Почему, собственно, нет? Имеет право!
Шли годы. Данный вид записи функции оброс слухами и легендами. В его мифологизацию внесла свой вклад и поп-масс-культура, выпустив пару музыкальных клипов с Кристиной Агилерой и тройку мерчей маек, сигарет, пива, и шариковых ручек с надписью Чё к ним, частично проспонсированных Ватиканом (это их маркетологам пришла идея, что всё это луче будет продаваться, если объявить запись Чёрча "Языком программирования Бога, на котором тот наваял Всё").
Шли годы ещё. Программисты теперь пишут функции по образцу имя(аргументы){тело} , а смутные обрывки о форме записи функций Чёрчем доступны в виде Тайных Знаний Гур и Лам. Преимущественно со скрепных территорий.
PS Ну, это тоже своего рода моё эссе о Лямбда-Исчислении.

vadimr
30.10.2023 14:09Примерно так это и понимают в масс-культуре.
Но в нашей реальности лямбда-исчисление придумали раньше, чем ЦВМ.

CrashLogger
30.10.2023 14:09+4Платоновские идеи гораздо лучше ложатся на ООП, чем на функциональщину. Идея круга - класс. Нарисованный на листе бумаги круг - объект этого класса. Любые круглые предметы - объекты, реализующие интерфейс "круглость". А любой процесс, происходящий в мире, гораздо проще разложить на шаги и выразить императивно, чем попытаться вывести некую универсальную формулу.

MasterMentor
30.10.2023 14:09+1Опоздали. Вопрос кругов в жизни "Мультивселенных" уже раскрыт автором в философском эссе Эйлер, Чёрч и Мандельброт — этюд о красоте и математике.
Там круг на весь экран (и не просто круг, а sic! круг с точкой посередине), и подпись:Чортов Чёрчев Черный КвадратМонада Пифагора.

werevolff
30.10.2023 14:09В принципе, ЯП - это абстракция. И ООП - это абстракция. И функциональное программирование - это абстракция. Круг - это тоже абстракция, которая позволяет выразить число Пи. Функциональное программирование позволяет выразить концепцию обработки данных. Концепция обработки данных позволяет выразить математические формулы. Математические формулы позволяют выразить правила и свойства пространства и времени, которые позволяют выразить то, что автор называет идеей. Некие законы бытия, правила для частиц и волн. И то, не факт, что это элементарные составляющие вселенной. ООП - это абстракция над функциональным программированием, которая позволяет объединять сходные данные и функции, а также, переиспользовать их или переопределять. Но всë это - лишь средство выражения, имеющее определëнные ограничения. Так, например, видимый или осязаемвй круг имеет погрешность реализации числа Пи. Функциональные языки имеют погрешность в представлении/хранении/обработке данных, а также, в реализации вычислений функций. С этой точки зрения, математика более точна, нежели информатика. Но, если возвращаться к вопросу того, что идеи Платона проще выразить через ООП, то следует помнить, что идея круга - это не класс, а функция. Идея многоугольников и многогранников - это углы, площадь и объëм. ООП лишь позволяет объединить эти формулы под общей абстракцией. Но, опять же, это даëт погрешность. Например, круг в ООП - что это? Напечатанная напринтере фигура? Или шаблон для станка? Или правила отрисовки для видеодвижка? ООП уводит нас от идеи - формулы - в сторону практической реализации, поскольку класс не может существовать без контекста его имплементации.

SimuliantSurrogatov
30.10.2023 14:09+1Почти обожаю этого автора! Стиль нечто) Наверное, когда он готовит себе завтрак, то это выглядит как-то так:
"Так, положим в тарелочку творога, немного докторской колбасы, пальмового масла... так - тёртый имбирь, столовую ложку соевого соуса, майонез, цедра лимона, кусочек сала... и, ох, да, чуть не забыл - заливаем все это квасом... ммм... предвкушаю вкусняшку...
И, пока я все это перемешиваю, я хотел бы поговорить с Вами подробно и по существу о Гаусовом исчислении и рангах компонент декартова разложения, чтобы было понятно как, в конце концов, в моей тарелке окажется замечательный жюлюен!"
Далее, напрягаться и писать какую-то обоснованную критику авторскому детищу смысла нет, ибо это как "об стену горох"! Это такой стиль изложения!
Но, все-таки, неплохо бы задуматься говоря о эпохи Античности на следующем, как говорится для общего образования:
Например, нет никакого "единства и борьбы противоположностей" (Гегель чуть опосля родился через где-то 15 веков) в понятиях Платона о материи и идеях, и фундаментально это не одно и тоже (идея и материя), а как раз фундаментально есть только идеи и всё!
Понятие "Бога" Античности нужно уточнять: безличное нечто существующее в замкнутом кругу перерождения в смысле циклинности и круговой замкнутости. Т.е. никакого Вам как пишет автор "создания" и "преобразования". В мире все создано и это множество постоянно и бессмысленно крутится по бесконечном кругу. Ничего не создаётся и не образуется! Нет идеи создания! Соответственно человек никакая не личность, а маленький атом в огромном космосе в надежде причаститься настоящей реальности "чистых идей" в философствовании.
Задуматься над термином создания! Ведь создание, это процесс появление того чего не было и одновременно почти полное отчуждение от него, ибо если созданное не автономно, то оно по сути и не созданно в полном смысле слова! И это один из серьёзных богословско-философских элементов проблематики акта божественного творения! И как пример разрешения этого - христианская идея богочеловечества и триадология.
Понятие человек в христианской этики, это не функция работающая с данными. Это трансцендентальная тайна. Это личность богоподобная.
Но, автору пофиг на эти нюансы, поэтому можно мешать тёплое с мягким ради красивого словца!
Мне нравится такое) Автор держит мозги читателя в тонусе. И задаёт интеллектуальное пространство для выяснения сути и деталей его скрытой на*бки! Спасибо искуситель абсурда!

z_lex
30.10.2023 14:09По первому пункту позволил бы себе уточнить: идея единства и борьбы противоположностей хоть и не связана напрямую с Платоном, но к античности имеет самое непосредственное отношение, т.к. была высказана еще Гераклитом, а в диалектике Гегеля уже получила свое развитие. В том, что нужно быть осторожнее, делая попытки связать такие широкие области знания - соглашусь

SimuliantSurrogatov
30.10.2023 14:09Благодарю за уточнение! Вы правы!
Единственный важный момент: Гераклиту принадлежит "идея единства противоположностей" и мир находится "просто" в состоянии постоянного движения и изменения, а вот "идея единства и борьбы противоположностей" - это уже Гегель, и мир связан с развитием (становлением) и эволюцией идей и понятий, в процессе преодоления противоречий через диалектическое движение тезиса, антитезиса и синтеза! Т.е. как такового понятия "развития" (появление нового) в Античности отсутствует!
Т.о. на примере контекста автора - волна и корпускула у Гераклита - эти понятия просто существующие противоречия перетекающие одно в другое, а у Гегеля эти понятия "развиваются" в единстве и борьбе формируя новое понятие - "корпускулярно-волновой дуализм" и далее находя новый антитезис, например "единство материи", снова синтез - ну, например "квантовая физика" и т.д. т.е. в мире происходит процесс создания нового, конечноже не в идеях "эволюции Дарвина и современного понятия прогресс", а в Гегельянской трактовке как глобальное становление абсолютного духа в самоотчуждении!

Dominux
30.10.2023 14:09-3Если язык Бога — это LISP
Но всем известно, что язык бога - это RUST

VadimTTavr
30.10.2023 14:09+5Это скорее язык дьявола (Максвелловского). А так-то бог, конечно, поймет Lisp, но родной-то у него Forth :-p

Wizard_of_light
30.10.2023 14:09+4Если Лисп язык бога, то языком дьявола будут конечные автоматы, потому что они полностью противоположны функциональной парадигме - не состояния преобразуются функциями, а функции реализуются последовательностью состояний.

JustMoose
30.10.2023 14:09Мне кажется, связывать религию и программирование не стоит.

MasterMentor
30.10.2023 14:09-1Эти бы ребята поспорили


SergioT4
30.10.2023 14:09Отпад башки.
Есть вера, а есть религия. Выглядит это как её худшие проявления религии, типа попросили сделать продакт-плейсмент.
Krey
30.10.2023 14:09На протяжении всей статьи, особенно философской ее части, витает мысль о том, что все мы живём в симуляции. Но почему-то не постулируется явно.

Hemml
30.10.2023 14:09+4Бог создал Lisp, а дьявол -- Common Lisp :)
В CL, при всей его лисповости, возможны такие грязные вещи, от которых стошнит и фортранщика. Но, именно потому что это Lisp, использование этих дьявольских кундштюков там возможно и даже полезно. То, от чего программа на другом языке превращается в гибрид макаронного монстра и атомной бомбы, в CL делает ее лишь быстрее.
Вообще, если мы уж коснулись вопросов божественного и дьявольского в языках программирования, то стоит упомянуть две книги -- SICP, как книгу "белой магии" программиста и "Common Lisp Recepies", как книгу черной магии. Обе про Lisp, что характерно.

Tschuess
30.10.2023 14:09Все смешалось в доме Облонских.
Смешались в кучу кони, люди, и залпы тысячи орудий слились в протяжный вой…





leshabirukov
Язык Ада же!