Каждому ученику 10-11 класса, желающему связать свою жизнь с профессиональной деятельности в IT-сфере необходимо запомнить две вещи:

1. Беречь зрение;

2. Научиться разрабатывать наилучшее алгоритмы для поиска решения заданной задачи.

Задача с параметром - это первая полноценная исследовательская задача, при решении которой, требуется применить как сообразительность, так и любовь к труду, потому как в процессе поиска решения придётся обработать бесконечное множество числовых элементов. Да и к тому же в распоряжении будущего абитуриента имеется всего около 4 часов на экзамен по математике (ЕГЭ), а значит нужно придумать для поиска решения такой рабочий алгоритм, который занимал бы минимум времени. Этим мы сейчас и займемся.

Надеюсь, среди читателей не найдется тех, кто всерьез решиться прогнать, с помощью выдуманной им программы (алгоритма на реальном коде), все числовые значения параметра "a", принадлежащее множеству действительных чисел в нижеприведенной задаче.

Однако, автор статьи будучи выпускником школы сам пытался "извратиться" и даже иногда применял для поиска решения в задаче с параметром табличный редактор "Excel". Но очевидные проблемы: дискретность значений параметра "a" и невозможность использования ноутбука даже на пробном экзамене поставили на таком методе - жирный крест "+".

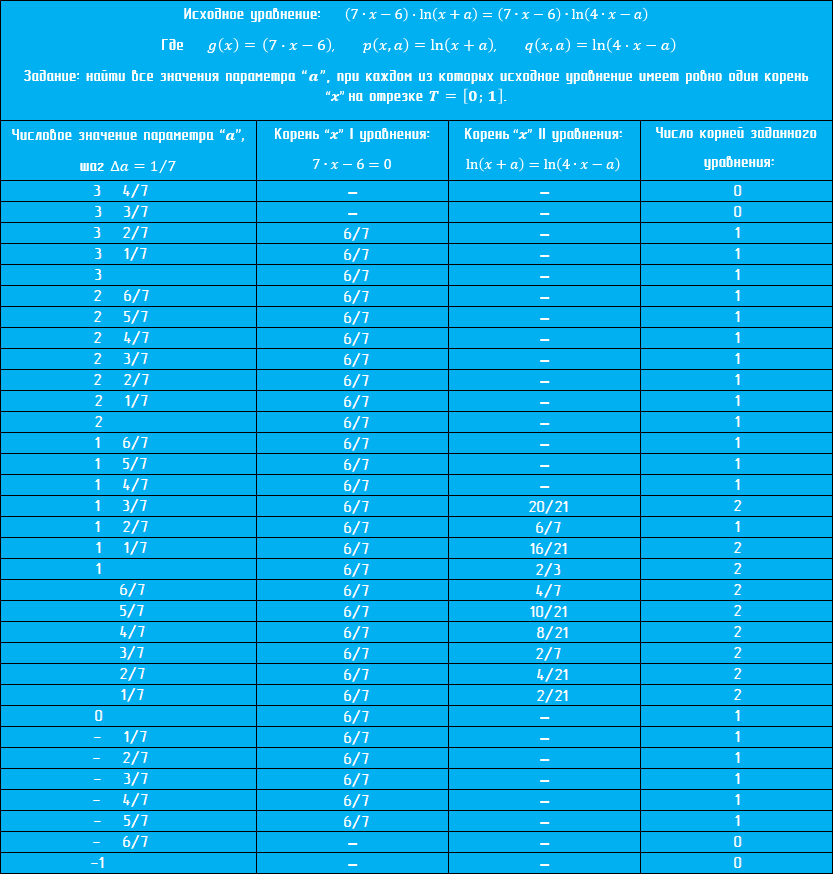
Но как тогда научиться быстро и главное правильно решать задачи с параметром? Для начала стоит поискать ответ на этот вопрос у своей интуиции, а лучше - логике.

Давайте подумаем о том: «А какая основная идея заложена для быстрого поиска правильного решения в данной задаче?».

Как ни странно, но ответ на этот вопрос очень простой: «Основной идеей для быстрого и правильного поиска решения — является способность видеть все возможные слои с необходимой информацией, а затем отбирать только полезные данные внутри каждого слоя» или короче «Овладеть навыком грамотной работы со слоистым мышлением».

Но кто такой этот «Слой»?

«Не помню такого студента, не учился он у меня...»

А если серьезно, то «Слой» — введенный мною термин вовсе не философская абстракция. И на протяжении данной статьи, я постараюсь это показать. Так например, каждый из Вас, читая данную статью, уже мыслит о ней по своему. То есть находится на своём «Слое». «Слой» — это (подумайте сами)...

Может «Слой» — это рандомно заполненные ячейки данными различных типов двухмерной таблицы или разряженная матрица, а может это оставшиеся живые нейроны после очередного стресса или вычислительные кластеры, применяемые инженерами в задачах CFD/FEM?

А ладно, хватит нам тут быть в роли «Нео» («Нео» — это главный герой‑исследователь в фильме «Матрица»)...

Сейчас мы рассмотрим графическую пародию на известнейший мем и обсудим важную тему: «Причинно‑следственная связь».

Наверняка Вы заметили, что «Синий пол» трехмерной сцены, сделанной в программе «КОМПАС-3D» подписан как «Причина», а должен был быть подписан так — «Фиолетовый цилиндр». И это не ошибка автора, это побуждения Вас и вашего мозга выстроить вполне логичную реакцию от уведенного нейронами мозга. А благодарить за такую «подлянку» стоит, как говорят психологи, ассоциативное мышление.

Чем больше времени за жизнь вы мыслите ассоциативно, тем тяжелее Вам будет решать задачи с параметрами. Поменяйте некое природное мышление на «Слоистое», т. е. такое — внутри которого есть какой‑то набор элементов (например, терминов из математики: параметры, числа, функции и т. д.), и проведите анализ относительно данных элементов по каким‑либо их главным признакам.

Поиграем сейчас в простую игру: «Вопрос‑ответ», а что бы Вам было проще в дальнейшем читать данную статью, ответьте на ряд следующих важных вопросов:

1. Какие существую способы задания функции?

2. Какие бывают функции?

3. Какие бывают числа?

4. Что такое числовая ось?

5. Что такое множество?

6. Какие я знаю методы решений задач с параметрами?

7. Когда параметр является числом, а когда функцией?

Задача автора данной статьи заключается в том, чтобы ты дорогой читатель поменял ассоциативное мышление на аналитическое, т.е. на такой тип мышления, который позволяет всесторонне анализировать имеющиеся данные (исходные и получаемые в результате решения задачи с параметром).

После того, как мы немного потренировали мозг, можно смело переходить к дальнейшему повествованию и постепенному раскрытию термина — «Слой» (применительно к задачам с параметром).

В задаче с параметром иногда приходиться рассуждать от очевидного из задачи следствия. Так к примеру, в задаче просят найти число корней (следствие) от параметра (причина), а Вы находите при конкретном числовом значении корня (следствие) — множество числовых значений параметра (причина). Что бы вытворять такие манипуляции и остаться в здравом уме, нужно оставлять своё сознание только в рамках используемого Вами «Слоя» и рассуждений над ним.

Так вот получается «Слой» — это частично обработанное и хранящее нашим мозгом множество знаний, т. е. состояние накопления полезных знаний до получения верного ответа на заданный вопрос.

А ответов, как и людей может быть очень много, причём, сколько людей, столько и ответов (в оригинале — мнений). В общем каждому экзаменатору студент не угодит) Ах да, вспомнил как раз анекдот на эту тему:

В идеале на нужном «N‑ом подслое» какого‑то «Слоя» должно находится некоторое множество знаний, содержащих строгий в математическом плане ответ на не менее грамотно сформулируемый вопрос.

Но что такое «Слой» в случае с задачей с параметром?

И можно ли уже наконец‑таки дать ответ на выше записанный вопрос однозначно и определенно?

Как показывает практика можно! В данном случае «Слой» — «Числовое множество». И при этом задача экзаменуемого найти такие числа, входящие во все «Числовые множества», которые обязательно подчиняются условию задачи. Получается, что ответом к задаче с параметром всегда является дискретная, кусочно‑заданная или непрерывная функция от параметра.

В математике задают функции не только аналитически, но и таблично, графически, и в том числе — описанием (хотя погодите, Вы же уже отвечали на этот вопрос и при этом — верно?). Поэтому наша задача при решении задач с параметром научиться находить «Множество значений параметра» удовлетворяющих условию, где условие — причина, а все отдельные числовые множества принадлежащие параметру — следствие.

Напоследок автор предлагает рассмотреть практический пример решения задачи с параметром с использованием теории множеств и применением формальной математической логики, дабы развеять туман над прочитанным Вами занудным текстом.

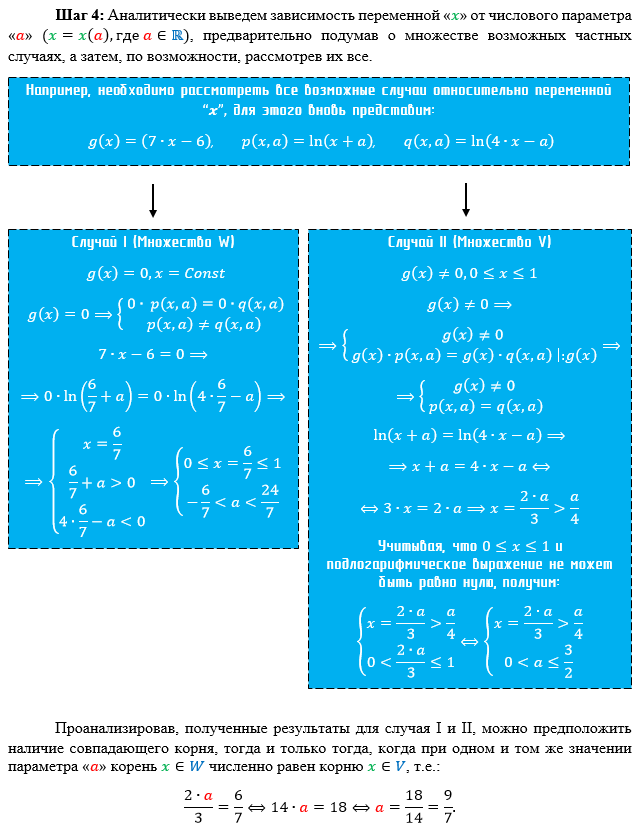
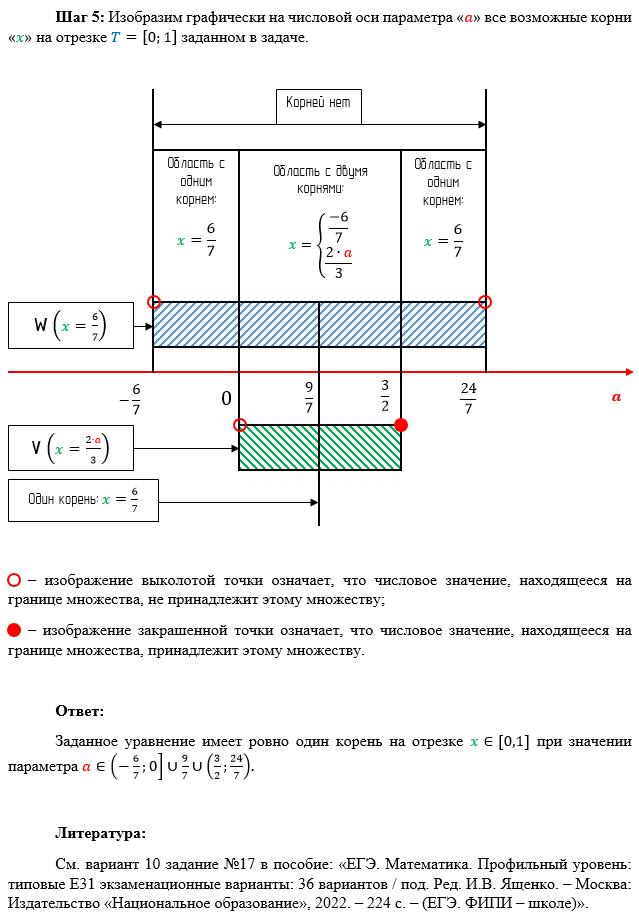
Всем спасибо за внимание!

Прокачивайте своё «Слоистое мышление» или как ещё его можно назвать — «Послойное мышление», и не забывайте прокачивать память, потому что без нее, вы не разберетесь в своих собственных записях, на одну задачу может уйти от 1 до 3 листков (см. пример автора статьи). А если не сможете прокачать память, записывайте важную промежуточную информацию (в идеале в блокнот, компьютер и e.t.c., ну а на экзамене обводите рамкой и называйте «Множеством»). А как подготовили материал — начинайте анализ.

Легче всего проводить анализ, если предварительно хорошо «отмасштабироваться»! «Масштабирование» — есть ни что иное, как сведение воедино всей полезной информации (О.О.Ф., все возможные зависимости от корней параметра и наоборот и т. д.).

Проще говоря, если Вы хотите доехать на такси в роли пассажира куда‑то заблаговременно, то предварительно нужно выбрать оптимальный по времени маршрут, а это нереализуемо без знаний у водителя о всех возможным маршрутах. Также лично Вам (пассажиру) желательно учесть и другие параметры, например, такие как: мотивация для водителя (чаевые), мощность двигателя, стаж вождения транспортного средства, оставшийся запас горючего, знания дорог и их состояние на местности и т. п.

P. S. Давайте вместе поможем будущем абитуриентам сдать ЕГЭ по математике на наивысший балл (100 вторичных баллов), для этого каждый, при желании, может посоветовать хорошую литературу по теме: «Решение задач с параметрами (Самоучитель)». Ну а я, пожалуй, начну:

1) Натяганов В.Л., Лужина Л.М. Методы решения задач с параметрами: Учеб. пособие. — М.: Изд-во МГУ, 2003. — 368 с.