У каждого разработчика есть набор инструментов для решения различных задач. Однако со временем возникает необходимость расширять этот набор, чтобы эффективно справляться с более сложными задачами. В этой статье я хочу познакомить вас с инструментом, которым вы, скорее всего, раньше не пользовались. И хотя он подходит для решения узкого спектра задач, его использование может оказаться весьма полезным. Знакомьтесь — "фильтр Блума" (Bloom filter).

Предполагается, что вы имеете представление о хэш-функциях. Если нет, рекомендую прочитать эту статью. Она позволит вам лучше понимать, о чем идет речь в этой статье.

Что может фильтр Блума?

Фильтр Блума похож на структуру данных Set. Он позволяет добавлять элементы в структуру и проверять их наличие. Ниже приведен пример использования фильтра Блума в JavaScript с вымышленным классом BloomFilter:

let bf = new BloomFilter();
bf.add("Ant");
bf.add("Rhino");
bf.contains("Ant"); // true
bf.contains("Rhino"); // true

Это выглядит похоже на Set, но существуют некоторые ключевые отличия. Фильтр Блума — это вероятностная структура данных. В отличие от Set, которая дает точный ответ "да" или "нет" при проверке наличия элемента, фильтр Блума предоставляет вероятностный ответ. Он может точно определить, что элемент отсутствует, но не может гарантировать наличие элемента.

В приведенном выше примере, мы спрашиваем bf, содержит ли он "Ant" и "Rhino". Возвращенное значение true не является абсолютной гарантией их наличия. Мы только что добавили эти элементы, но существует вероятность, что фильтр Блума даст ложноположительный ответ:

let bf = new BloomFilter();
bf.add("Ant");
bf.add("Rhino");
bf.contains("Fox"); // true

Почему так? Когда фильтр Блума возвращает значение true, это означает "возможно", а не "да". Если элемент, который никогда не добавлялся в фильтр Блума, все же отмечен как присутствующий, это считается ложноположительным результатом.

И наоборот, когда фильтр Блума возвращает значение false для ранее добавленного элемента, это называется ложноотрицательным результатом. Фильтр Блума никогда не дает ложноотрицательных результатов, что делает его очень полезным.

Как может быть полезной структура данных, которая дает ложные результаты?

Не совсем ложные, скорее неоднозначные. Рассмотрим пример, где можно использовать это свойство с пользой для дела.

Когда фильтр Блума полезен?

Предположим, что мы разрабатываем веб-браузер и хотим защитить пользователей от вредоносных ссылок. Вместо создания и поддержки списка всех известных вредоносных ссылок, можно использовать фильтр Блума. Он позволит эффективно и быстро проверять ссылки пользователя на вредоносность. Это может сэкономить ресурсы и повысить производительность браузера.

Допустим, существует 1 000 000 вредоносных ссылок по 20 символов каждая, что составляет 20 МБ. Однако, если мы готовы принять вероятность ошибки в 0,0001% (1 на миллион), можно использовать фильтр Блума. Это позволит хранить те же данные всего в 3,59 МБ. Или, при допущении ошибки в 0,1% случаев (1 на 1000), размер данных составит всего 1,8 МБ.

Применение фильтра Блума не является гипотетическим — до 2012 года Google Chrome использовал его для защиты от вредоносных ссылок. Что касается ложных срабатываний, то можно создать API с полным списком вредоносных ссылок в базе данных. Так мы сможем проверять ссылку только в случае предполагаемой угрозы, избегая лишних вызовов API для каждой ссылки. В результате — меньше ложных срабатываний и серьезная оптимизация производительности.

Принцип работы фильтра Блума

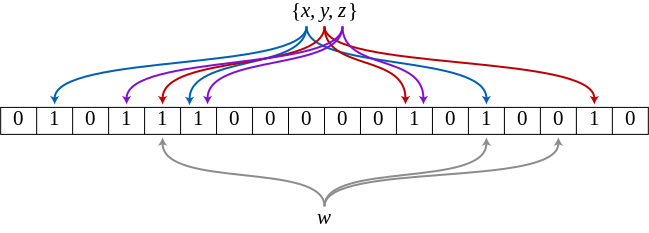
Фильтр Блума — это массив битов, все значения которых изначально равны 0. Его можно представить в виде сетки, где каждый бит соответствует окружности. Во всех приведенных ниже примерах, фильтр Блума будет содержать в общей сложности 32 бита.

Чтобы добавить элемент в фильтр Блума, мы используем 3 различные хэш-функции для получения 3 значений, затем устанавливаем соответствующие 3 бита. В данной статье я использую 3 хэш-функции семейства SHA (sha1, sha256 и sha512). Вот как будет выглядеть фильтр Блума после добавления в него значения "foo":

Значения установлены только в позициях 15, 16 и 27.

Мы берем хэш-значение "foo" для каждой из 3 хэш-функций и умножаем его по модулю на количество бит в фильтре Блума. При делении на 32 получаем остаток по модулю. Хэш-функции sha1, sha256 и sha512 дают нам значения 27, 15 и 16 соответственно.

В примерах ниже можно увидеть, какие биты будут установлены при разных значениях.

Вот что происходит при добавлении собственных значений в фильтр Блума:

Можно заметить, что в некоторых случаях задаются только 2 бита, или даже один. Это происходит, когда 2 или более хэш-функции возвращают одинаковое значение или при попытке установить бит, который уже установлен.

Но… Если установлен каждый бит, то не будет ли фильтр Блума утверждать, что содержит все элементы, которые проверяются? Результат всегда будет ложноположительным!

Совершенно верно. Если все биты фильтра Блума будут установлены, он будет эквивалентен Set, который всегда возвращает значение true для операции contains. Фильтр Блума будет утверждать, что содержит все элементы, независимо от того, были они добавлены или нет.

Частота ложноположительных результатов

Частота ложноположительных результатов в фильтре Блума растет по мере увеличения процента установленных битов.

При установке всех битов частота ложноположительных результатов будет максимальной. Это связано с вероятностной природой фильтра Блума и количеством хэш-функций. Это объясняется формулой, согласно которой частота ложноположительных результатов вычисляется как x ^ 3, где x — процент установленных битов, а 3 — количество используемых хэш-функций. Для наглядного примера рассмотрим фильтр Блума, где установлена половина битов (т.е., x = 0.5). Предположим, что хэш-функция имеет равную вероятность установки любого из битов. В таком случае, вероятность того, что все 3 хэш-функции установят уже установленный бит, будет равна 0.5 * 0.5 * 0.5, или x ^ 3.

Рассмотрим влияние количества хэш-функций на частоту ложноположительных результатов.

Похоже, чем больше хэш-функций используется, тем ниже вероятность ложноположительных результатов. Означает ли это, что всегда нужно использовать много хэш-функций? Почему бы не использовать, например, 100 таких функций?

Проблема с использованием большого количества хэш-функций заключается в том, что это приводит к быстрому заполнению фильтра. Каждая дополнительная хэш-функция требует установки дополнительных битов для каждого добавляемого элемента. Кроме того, увеличение числа хэш-функций также увеличивает их стоимость. Хотя хэш-функции, используемые в фильтре Блума, оптимизированы для быстрой работы, запуск 100 хэш-функций все равно требует больших ресурсов, чем запуск, например, 3 функций.

Можно рассчитать, насколько заполнен фильтр Блума после добавления определенного количества элементов, основываясь на количестве используемых хэш-функций. На графиках ниже показан пример для фильтра Блума, в котором содержится 1000 бит.

Использование большого количества хэш-функций приводит к более быстрому установлению всех битов. Как можно видеть на графике, кривая уменьшается по мере добавления новых элементов. Это объясняется тем, что с увеличением числа хэш-функций вероятность повторного установления уже установленных битов увеличивается.

На деле, 1000 бит — небольшой размер фильтра Блума, занимающий всего 125 байт памяти. У современных компьютеров большой объем памяти, поэтому с увеличением размера фильтра до 100 000 бит (12,5 КБ) можно получить более точные результаты.

Линии едва выходят за пределы нижней части графика. Это означает, что фильтр Блума будет содержать очень мало установленных битов, и частота ложноположительных результатов будет низкой. Это достигается при размере фильтра Блума в 12,5 КБ памяти, что для современных стандартов по-прежнему очень мало.

Настройка фильтра Блума

При выборе количества хэш-функций и битов для фильтра Блума важно соблюдать баланс. К счастью, если мы заранее знаем сколько уникальных элементов хотим сохранить, а также желаемую частоту ложноположительных результатов, можно рассчитать оптимальное количество хэш-функций и требуемое количество битов.

На странице фильтра Блума в Википедии описана математика, которую можно использовать для расчетов. Я переведу эту математику в функции JavaScript. Однако не обязательно разбираться в математике, чтобы использовать фильтр Блума или читать эту статью. Я привел ссылку на эту страницу только для полноты картины.

Оптимальное количество битов

Для определения оптимального количества битов воспользуемся следующей функцией JavaScript. Несмотря на то, что она может показаться сложной, она принимает всего два параметра: количество элементов, которое мы хотим сохранить (items), и желаемую частоту ложноположительных результатов (fpr, где 1% равно 0,01). Функция возвращает количество битов, которое потребуется для достижения желаемой частоты ложноположительных результатов.

function bits(items, fpr) {
  const n = -items * Math.log(fpr);
  const d = Math.log(2) ** 2;
  return Math.ceil(n / d);
}

Вот как этот показатель меняется для различных значений fpr:

Оптимальное количество хэш-функций

Для вычисления оптимального количества хэш-функций можно использовать следующую функцию:

function hashFunctions(bits, items) {
  return Math.ceil((bits / items) * Math.log(2));
}

Вот как количество хэш-функций будет меняться в зависимости от размера фильтра Блума и количества добавляемых элементов:

Чем больше элементов планируется добавить, тем меньше хэш-функций должно использоваться. С другой стороны, чем больше размер фильтра Блума, тем больше хэш-функций можно использовать. Большее количество хэш-функций уменьшает вероятность ложноположительных результатов. Однако увеличение количества элементов может привести к быстрому заполнению фильтра Блума.

Математики провели сложные исследования, чтобы помочь нам найти правильный баланс между количеством хэш-функций, размером фильтра и количеством элементов.

Предостережение

Важно обращать внимание на оценку количества элементов, которые планируется добавить, и выбор уровня ложноположительных результатов, который является приемлемым для конкретного случая использования. При подборе оптимального количества битов и хэш-функций, все зависит от точности этих оценок.

Если оценить эти параметры сложно, я рекомендую перестраховаться. Может быть лучше использовать фильтр Блума большего размера, чем предполагалось. Это снизит вероятность ложноположительных результатов и повысит надежность фильтра.

Удаление элементов из фильтра Блума

Вся статья была посвящена добавлению элементов в фильтр Блума и выбору оптимальных параметров. Однако мы не затрагивали процесс удаления элементов, и не случайно.

В фильтре Блума для отслеживания наличия элементов используются биты, представленные нулями и единицами. Однако, если попытаться удалить элемент, просто установив его биты в ноль, можно случайно удалить и другие элементы. Нет способа точно определить, какие элементы были удалены.

Наглядно представим этот процесс. Сначала добавим элемент "foo":

Затем добавим "baz":

Затем удалим элемент "baz":

В результате фильтр Блума не содержит ни "baz", ни "foo". Это происходит из-за того, что оба элемента устанавливают бит 27, что приводит к затиранию информации о наличии "foo" при удалении "baz".

Кроме того, если добавить элемент "foo", а затем попытаться удалить "baz" до его добавления, ничего не произойдет. Это связано с тем, что биты 18 и 23 не были установлены и фильтр Блума не содержит информации о наличии "baz". Поэтому бит 27 не обнуляется.

Фильтр Блума с подсчетом

Фильтр Блума с подсчетом представляет собой вариант фильтра Блума, в котором можно удалять элементы. Для этого вместо битов используется массив счетчиков.

Произведем те же операции и попытаемся удалить элемент "baz".

Фильтр все еще содержит "foo". Проблема решена.

Однако, у этого подхода есть один недостаток: счетчики занимают больше места, чем биты. Счетчик из 4 битов позволяет увеличивать значение до 15, а счетчик из 8 битов — до 255. Нужно выбирать размер счетчика таким образом, чтобы он никогда не достигал своего максимального значения, иначе появляется риск повреждения фильтра. Использование в 8 раз большего объема памяти, чем в стандартном фильтре Блума, может стать камнем преткновения, особенно если основная цель — экономия памяти. Поэтому важно решить, действительно ли нам нужна возможность удалять элементы из фильтра.

Фильтр Блума с подсчетом может давать ложноотрицательные результаты, которые невозможны в стандартном фильтре. Рассмотрим следующий пример. Добавим элемент "loved" и удалим "response".

Поскольку и "loved", и "response" имеют хэш-значения 5, 22 и 26, при удалении "response", удаляется и "loved". Запишем это в JavaScript и проблема станет более понятной:

let bf = new CountingBloomFilter();
bf.add("loved");
bf.add("your");
bf.remove("response");
bf.contains("loved"); // false

Мы уверены, что добавили элемент "loved" в фильтр, но при вызове contains получаем false. Такие ложноотрицательные результаты невозможны при использовании стандартного фильтра Блума, а ведь именно в этом заключается его основное преимущество: гарантия отсутствия ложноотрицательных результатов.

Практическое применение фильтра Блума

Akamai — одна из компаний, которая успешно использует фильтр Блума. Они применяют его для предотвращения кэширования веб-страниц, доступ к которым происходит всего один раз. Для этого они сохраняют все запросы к страницам в фильтре Блума и кэшируют их только в том случае, если фильтр Блума указывает, что эти страницы уже просмотрены ранее. И хотя некоторые страницы кэшируются при первом обращении, это незначительные потери. Вместо хранения всех запросов к страницам в Set, в Akamai предпочитают небольшое количество ложноположительных результатов в пользу более компактного фильтра Блума. Компания Akamai опубликовала статью, где все это подробно описывается.

Google BigTable, распределенное хранилище значений по ключам, также использует фильтр Блума, чтобы определять, какие ключи содержатся в базе данных. Когда поступает запрос на чтение ключа, BigTable сначала проверяет фильтр Блума, чтобы определить, находится ли ключ в базе данных. Если ключа нет в фильтре, BigTable сразу отвечает "не найден", не прибегая к чтению данных с диска. Могут возникать некоторые ложноположительные результаты, когда фильтр Блума ошибочно указывает, что ключ может быть в базе данных, хотя его там нет. Однако последующий доступ к диску подтверждает отсутствие ключа в базе данных.

Заключение

Фильтр Блума представляет собой замечательный пример использования хэш-функций и осознанного компромисса для достижения конкретных целей.

В разработке программного обеспечения часто применяются компромиссы и комбинирование простых элементов для создания более сложных и специализированных структур данных. Умение определить, когда и где использовать определенную структуру данных может выделить вас среди других разработчиков и вывести вашу карьеру на новый уровень.

Полезные ссылки:

• Что такое фильтр Блума?
• Фильтр Блума – вероятностная структура данных для проверки принадлежности элемента множеству
• Реализация фильтра Блума на JS

---