Всем привет. В этой статье я расскажу про дерево отрезков. Дерево отрезков - это очень мощная структура данных, которая позволяет делать много разных операций над массивом чисел. Я постараюсь по полочкам разложить эту тему и объяснить возможности дерева отрезков. Также я разберу несколько нетривиальных задач на дерево отрезков. Помимо самого дерева отрезков я расскажу и про связанные темы: дерево Фенвика, разреженные таблицы.

Материал был подготовлен на основе лекций Павла Маврина (Канал на YouTube), статьи на e-maxx (Статья) и курса АиСД от Тинькофф (Курс). Примеры кода будут написаны на C++.

Первая задача

Условие
Дан массив arr целых чисел размером n. Необходимо выполнить m запросов. Каждый запрос выглядит так:

• sum(l,r) - необходимо найти сумму отрезка от l до r - 1 и вернуть ее. Формально: sum(l,r) = a[l] + a[l + 1] + ... + a[r - 1]

Решение
Вычислим префиксные суммы от массива arr. Полученные значения внесем в массив prefix
Тогда ответ на каждый запрос sum(l,r) будет выглядеть так: sum(l,r) = prefix[r] - prefix[l]

Код

vector<int> arr;  
vector<int> prefix;  
  
void build() {  
	prefix.push_back(0);  
	int b = 0;  
	for (int i: arr) {  
		b += i;  
		prefix.push_back(b);  
	}  
}  
  
int sum(int l, int r) {  
	return prefix[r] - prefix[l];  
}

Сложность
Построение префиксных сумм имеет сложность O(n), а сам ответ на запрос будет за O(1)

Вторая задача

Условие дополняется
Дан массив arr целых чисел размером n. Необходимо выполнить m запросов. Каждый запрос выглядит так:

• sum(l,r) - необходимо найти сумму отрезка от l до r - 1 и вернуть ее. Формально: sum(l,r) = a[l] + a[l + 1] + ... + a[r - 1]

• set(i, v) - меняет значение у элемента arr[i] на v

В таком случае использование префиксных сумм является неоптимальным решением, потому что, когда у нас меняется элемент arr[i], то все префиксные суммы находящиеся правее этого элемента необходимо также обновить. Получается запрос на изменение будет за O(n)

void set(int i, int v) {  
	arr[i] = v;  
	for (int j = i + 1; j < prefix.size(); ++j) {  
		prefix[j] = prefix[j - 1] + arr[j];  
	}  
}

В таком случае можно использовать дерево отрезков, который позволяет изменять элемент и получать сумму на отрезке за O(logn)

Дерево отрезков

Подготовка

Дерево отрезков - это дерево, как бы странно это не звучало. Мы хотим, чтобы это дерево выглядело приятно и удобно. Поэтому сделаем наше дерево двоичным деревом- то есть деревом, у которого каждый узел имеет не более двух потомков. Но в отличие от стандартного определения двоичного дерева у нас каждый узел будет иметь либо двух потомков, либо вообще не иметь потомков. Тут возникает проблема, что если длина массива arr не является степенью двойки, то тогда дерево будет выглядеть не очень удобно. Поэтому для упрощения мы дополним массив нулями, пока его длина не станет равна степени двойки. В теории, если необходимо сэкономить память, то можно пользоваться и форматом дерева, где длина не равна степени двойки, но мы будем использовать увеличение длины массива до степени двойки, чтобы было удобнее.

При увеличении длины массива до степени двойки получившаяся длина не превысит 2*n, потому что даже если взять худший случай (когда изначальная длина массива на один больше степени двойки k, то есть n = 2^k + 1), то нам придется добавить 2^k - 1 элементов в массив. Преобразуем и получим, что количество добавленных элементов будет равно n - 2. У нас был массив длиной n, мы в худшем случае добавили n - 2 элементов и получили 2n - 2 - максимальную верхнюю границу.

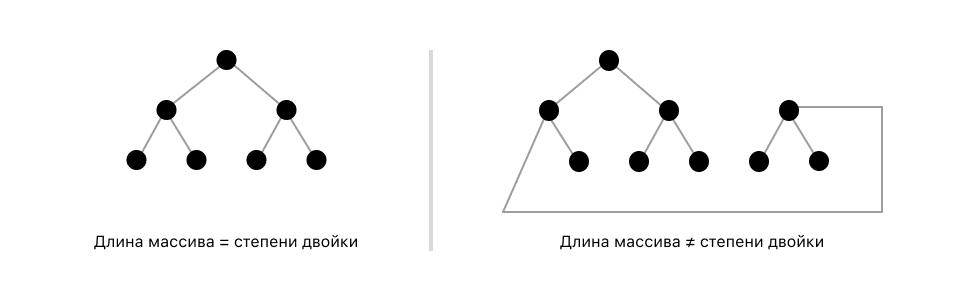
То есть перед тем, как продолжать работу, необходимо увеличить длину массива до степени двойки

#include <cmath>
void resize(vector<int> &arr) {  
	int s = (int) arr.size();  
	int new_s = (int) pow(2, ceil(log2(s)));  
	arr.resize(new_s, 0);  
}

Структура дерева

Дерево отрезков для этой задачи будет выглядеть так:

• листы дерева (то есть узлы без потомков) - это изначальный массив чисел

• каждый узел, который не является листом - это сумма двух его потомков

Постройка дерева

Построить такое дерево можно за O(n). Для хранения дерева будем использовать обычный массив длиной 2n (На деле одна клетка в массиве будет не занята, но это ни на что не влияет). Такая длина, потому что при поднятие вверх по уровням дерева количество элементов на определенном уровне в два раза меньше, чем на уровне ниже. И получается самый нижний уровень хранит n элементов, предпоследний n/2 и так далее до 1. Это геометрическая убывающая последовательность. Если подсчитать сумму, то получится 2n - 1, округлим для удобства до 2n.

Как хранить дерево в массиве? Очень просто, будем распределять элементы сверху вниз, слева направо. Тогда корневой узел у нас будет иметь индекс 0, его дети 1 и 2 и так далее вниз. Более формально это можно описать так: left of i = 2*i + 1 и right of i = 2*i + 2

В таком случае, все четные индексы, кроме нуля, являются правыми детьми, а нечетные индексы являются левыми детьми.

Иногда можно будет увидеть реализацию, где корневой узел имеет индекс 1, так тоже можно делать, но лично для меня удобнее работать с нуля.

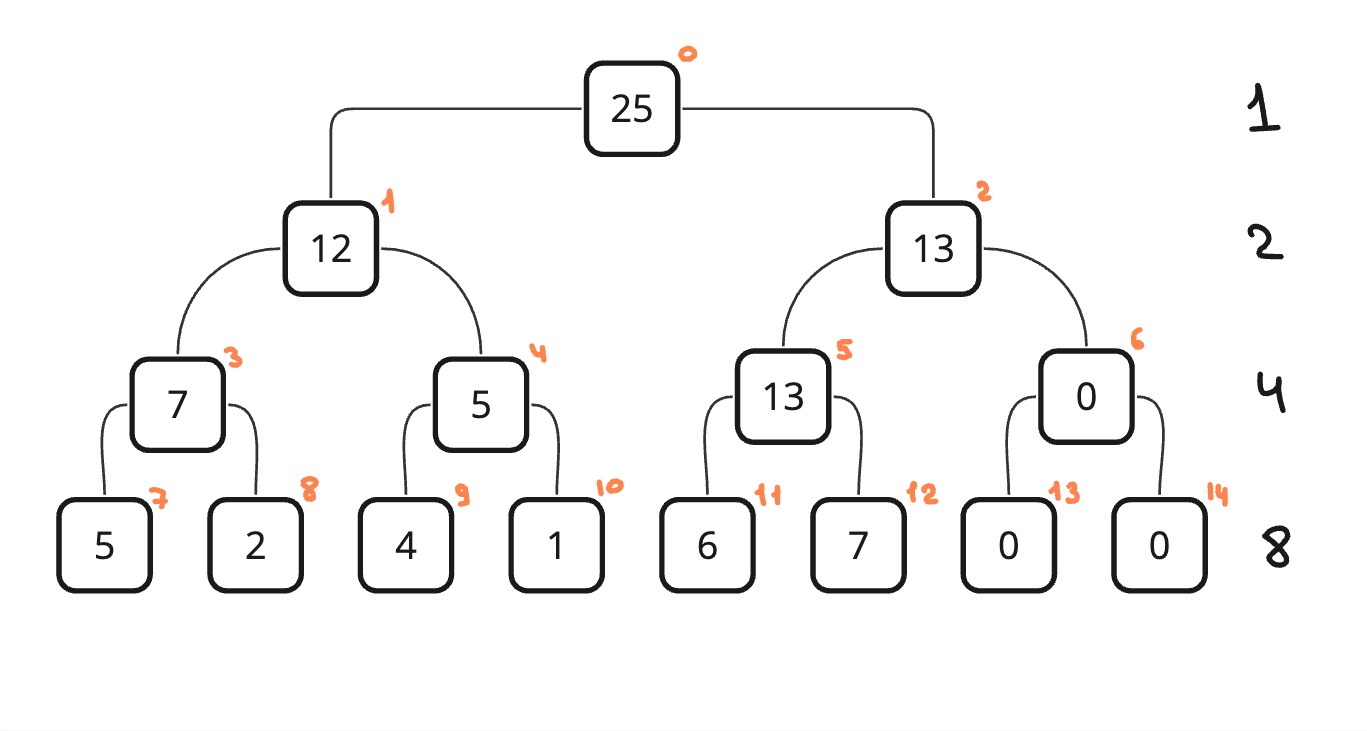
Как я и писал выше "каждый узел, который не является листом - это сумма двух его потомков", но что еще означает каждый узел?
Он означает сумму на определенном отрезке. Допустим возьмем индекс 10. Эта вершина будет обозначать сумму на отрезке [3, 3], где 3 - это индекс из оригинального массива.
Другой пример: индекс 1. Он означает сумму на отрезке [0, 3]. И так работает с любым узлом в дереве.

Как же построить такое дерево?
Будем делать это рекурсивно, начиная с вершины. Алгоритм будет выглядеть так:

• Принимаем массив, на основе которого строим дерево, текущую вершину (индекс вершины) и левую и правую границу

• Если левая и правая граница сжались до одного элемента, то устанавливаем этот элемент

• Иначе, находим середину и рекурсивно запускаем алгоритм заново

  • Первый запуск - левые дети

  • Второй запуск - правые дети

• Обновляем значение в текущей вершине

Код выглядит так:

class segtree {
public:
	vector<int> t;
	int n;
	
	segtree(vector<int> &arr) {  
		n = (int) arr.size();  
		t.resize(2 * n);  
		build(arr, 0, 0, n);  
	}

private:  
	void build(vector<int> &arr, int v, int tl, int tr) {  
	    if (tl == tr - 1) {  
		    t[v] = arr[tl];  
	    } else {  
		    int tm = (tl + tr) / 2;  
		    build(arr, v * 2 + 1, tl, tm);  
		    build(arr, v * 2 + 2, tm, tr);  
		    t[v] = t[v * 2 + 1] + t[v * 2 + 2];  
	    }  
  }
}

Рассмотрим алгоритм по шагам:
Пусть n = 8, тогда мы запустим функцию build с v = 0, tl = 0, tr = n
Рассмотрим самый левый путь. Мы будем сжимать наш текущий отрезок (который изначально был [0, n - 1], n - 1 потому что мы работаем с r - 1) до такого состояния, что tl == tr - 1. В случае с самым левым путем мы сожмем его до [0, 0], после чего мы произведем изменение массива t[7] = arr[0]. 7 потому что мы при каждом вызове функции будем уходить влево и менять v на 2*v - 1. По картинке выше можно отследить как будем меняться v. После изменения массива мы выйдем из этого вызова и поднимемся на уровень выше. И пойдем в правую сторону. После того как правая сторона обработается у нас получится, что t[7] = arr[0] и t[8] = arr[1]. А t[3] = t[7] + t[8]. И так будет продолжаться, пока не мы не выйдем из вызовов и не вернемся к первому вызову, где обработается t[0]. В итоге получится построенное дерево отрезков.

Также стоит отметить, что дерево можно построить и не прибегая к рекурсии. Также можно строить дерево снизу вверх, а не как в нашем случае сверху вниз. Эти методы разберем ниже.

Изменение элемента в массиве

После постройки дерева можно уже переходить к самим операциям. Начнем с более легкого - изменение элемента в массиве. Напомню, как звучит сама операция:

• set(i, v) - меняет значение у элемента arr[i] на v

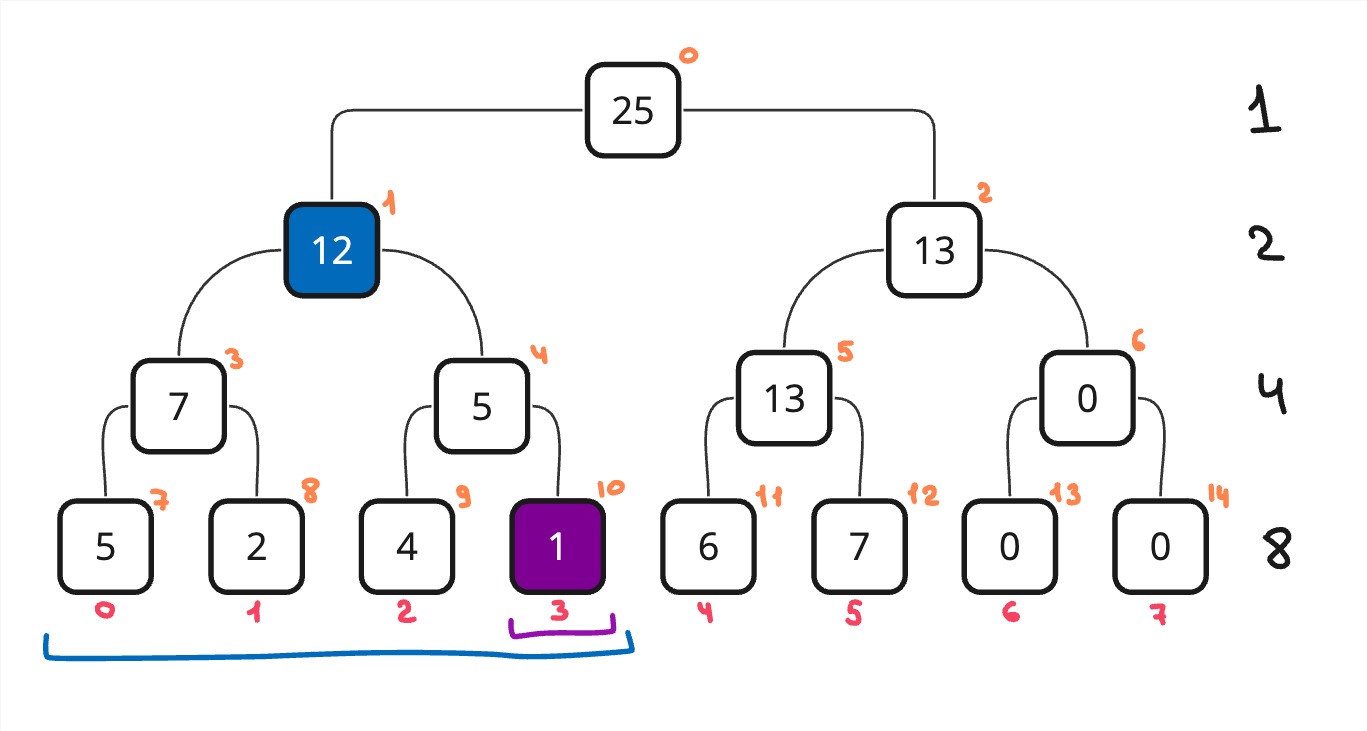
Разберем изменение элемента на примере: допустим нам надо поменять элемент с индексом 4 на 1. В таком случае кроме самого элемента нам нужно пересчитать все вершины до корня. Так как строили мы дерево сверху вниз, то и изменять будем сверху вниз. Начинаем с корня (текущая вершина с индексом 0) и границами xl, xr равными 0, n соотвественно. Находим середину границ и смотрим какой ребенок нам подходит. Заходим в подходящего нам ребенка. То есть вначале у нас будет середина равна 4. Это значит, что все левые дети лежат на отрезке [0, 3], а правые [4, 7]. Нам подходит правый ребенок, поэтому мы переходим в него. Повторяем все то же самое до тех пор, пока не сожмем границы до одного числа. В нашем случае это будет [4, 4]. Тогда мы поменяем элемент в массиве и начнем выходить из рекурсии. На выходе мы пересчитываем вершину выше. То есть просто заново вычисляем ее.

void set(int i, int v, int x, int xl, int xr) {  
	if (xl == xr - 1) {  
		t[x] = v;  
		return;  
	}  
	int xm = (xl + xr) / 2;  
	if (i < xm) {  
		set(i, v, 2 * x + 1, xl, xm);  
	} else {  
		set(i, v, 2 * x + 2, xm, xr);  
	}  
	t[x] = t[2 * x + 1] + t[2 * x + 2];  
}

Сложность
Такой алгоритм будет работать за O(logn), потому что глубина нашего дерева не превышает logn и на каждой итерации мы выбираем в левого или правого ребенка мы будем заходить.

Поиск суммы на отрезке

Задача звучала так:

• sum(l,r) - необходимо найти сумму отрезка от l до r - 1 и вернуть ее. Формально: sum(l,r) = a[l] + a[l + 1] + ... + a[r - 1]

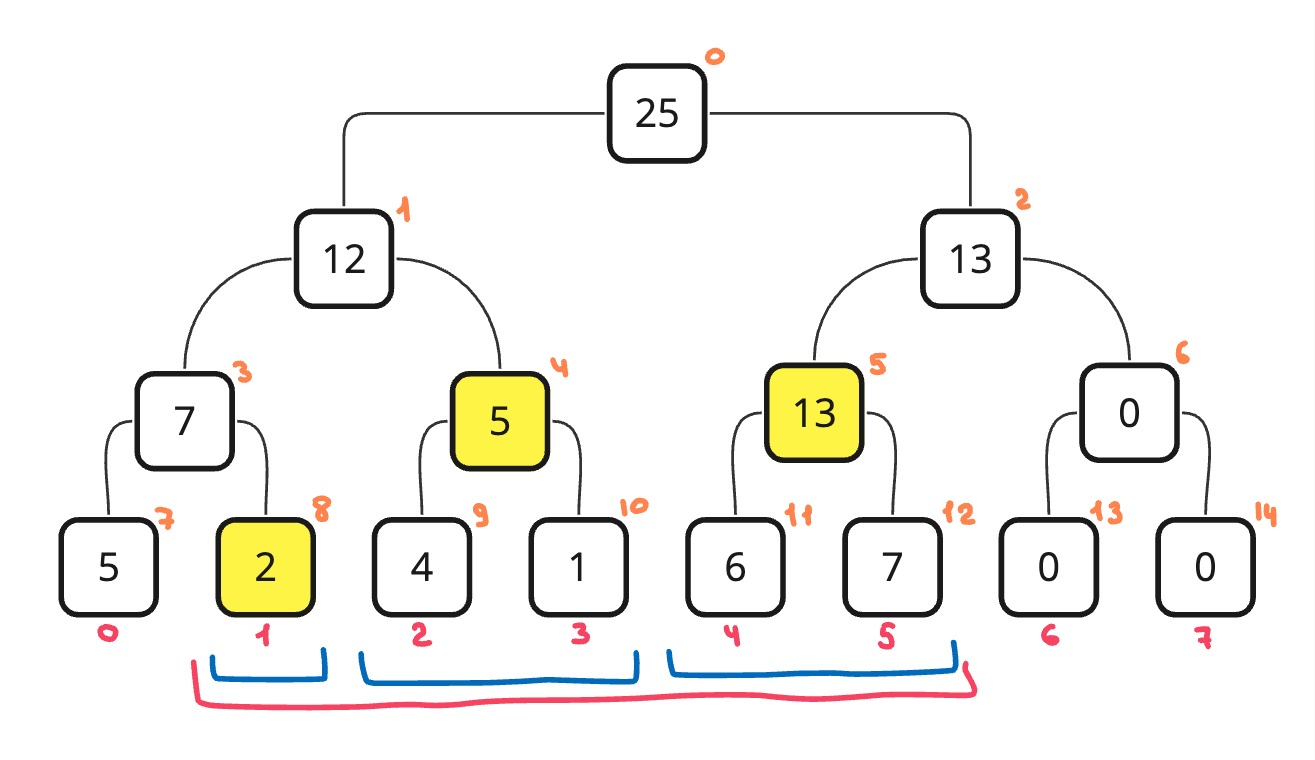
Допустим нам нужно вычислить сумму на отрезке [1, 5], тогда мы разобьем этот отрезок на несколько маленьких отрезков (на картинке это синие отрезки). Их значения мы уже знаем, мы просто сложим эти значения и вернем ответ.

Как это реализовать. Все, как всегда начинается с корня и с границами xl = 0, xr = n. Но тут есть нюанс. В какой-то момент в функции может быть три варианта границы:

1. Граница вышла за отрезок

2. Граница полностью внутри отрезка

3. Граница частично внутри отрезка

1. В первом случае нам необходимо выйти из функции, потому что вниз невозможно спуститься так, чтобы границы вошли в отрезок

2. Во втором случае мы возвращаем значение вершины

3. А в третьим случае мы делим наши границы на две части и отправляемся в левого и правого ребенка. После чего возвращаем итоговую сумму этих двух частей.

long long sum(int l, int r, int x, int xl, int xr) {  
	if (r <= xl || l >= xr) {  
		return 0;  
	}  
	if (xl >= l && xr <= r) {  
		return t[x];  
	}  
	int xm = (xl + xr) / 2;  
	return sum(l, r, 2 * x + 1, xl, xm) + sum(l, r, 2 * x + 2, xm, xr);  
}

Сложность
Сложность будет O(logn), потому что количество третьих случаев не превысит 2logn, а в целом в дереве рекурсии количество вызовов не превысит 4logn - 1

Вот и все, самое обычное дерево отрезков готово. Но на этом задачи не заканчиваются. Продолжим разбирать задачи и возможности дерева отрезков.

Дерево отрезков без рекурсии

Постройка выглядит просто. Вначале мы заносим в листы значения из оригинального значения. Первый элемент оригинального массива хранится в n - 1 элементе в дереве. Потому что до этого элемента в дереве есть n - 1 элементов. После чего в отдельном цикле мы проходимся по всем узлам, которые не являются листьями и вычисляем для них значения. Главное проходится во втором цикле с конца, потому что если мы начнем с нуля, то у нас будет t[0] = t[1] + t[2], но t[1], t[2] еще не вычислены и дерево не построится для слоев кроме последнего и предпоследнего.

void build(vector<int> &arr) {  
	n = (int) arr.size();  
	t.resize(2 * n);  
	for (int i = 0; i < n; i++) {  
		t[n + i - 1] = arr[i];  
	}  
	for (int i = n - 1; i > 0; i--) {  
		t[i] = t[2 * i + 1] + t[2 * i + 2];  
	}  
}

Изменение элемента
Вначале меняем элемент, а потом поднимаемся вверх до корня и исправляем значения.

void set(int i, int v) {  
	int x = n + i - 1;  
	t[x] = v;  
	while (x != 0) {  
		x = (x - 1) / 2;  
		t[x] = t[2 * x + 1] + t[2 * x + 2];  
	}  
}

Поиск суммы на отрезке
Здесь придется немного повозиться. У нас есть левая и правая граница. Нам необходимо научиться подниматься вверх и переносить границы. Существует 4 варианта:

• Левая граница является левым ребенком. Тогда мы просто смещаем левую границу и делаем ее равной родителя.

• Правая граница является правым ребенком. Аналогичная ситуация

• Левая граница является правым ребенком. Тогда мы заносим в ответ левую границу. А также переносим ее, но не к родителю, а к соседнему к родителю узлу.

• Правая граница является левым ребенком. Аналогичная ситуация

Когда в первом и втором случае мы переносим границу вверх, то мы ничего не меняем. Левая граница всего отрезка никак не меняется. Мы просто поднялись наверх. А в третьем и четвертом случае безболезненно подняться невозможно, поэтому мы добавляем значение границы в ответ и поднимаемся вправо или влево. Правый или левый ребенок текущее значение определяем с помощью четности.

Код не очевиден и написан не точь-в-точь как было описано выше. Это связано с тем, что здесь показан итоговый вариант, включая определенные математические сокращения

int sum(int l, int r) {  
	l = l + n - 1;  
	r = r + n - 2;
	int ans = 0;  
	while (l <= r) {  
		if (l % 2 == 0) ans += t[l];  
		l = l / 2;  
		if (r % 2 == 1) ans += t[r];  
		r = r / 2 - 1;  
	}  
	return ans;  
}

Такой код будет работать за O(log(r - l)), потому что на каждой итерации цикла мы уменьшаем длину отрезка в два раза. Это может быть удобно, когда нам нужно часто искать сумму на коротких отрезках.

Персистентные деревья отрезков

Это дерево отрезков, которое хранит все версии дерева отрезков. Например, когда нам нужно изменить какой-нибудь элемент мы делаем делаем копию всего пути от корня до этой самой вершины и изменяем ее. В итоге в дереве получается два корня: первый - не измененный и второй - уже измененный. Подробнее про такие деревья можно на Хабре

Третья задача

Условие изменяется
Дан массив arr целых чисел размером n. Необходимо выполнить m запросов. Каждый запрос выглядит так:

• min(l,r) - необходимо найти минимум на отрезке от l до r - 1 и вернуть ее. Формально: min(l,r) = min(a[l], a[l + 1], ..., a[r - 1])

• set(i, v) - меняет значение у элемента arr[i] на v

Дерево отрезков можно использовать для любой ассоциативной операции, то есть для такой операции, в которой порядок не имеет значение. Минимум и максимум являются именно такими операция, потому что варианты min(1, 2, 3) = 1 и min(3, 2, 1) = 1 вернут одно и то же значение.

По сути код не очень сильно меняется. Есть всего два важных момента:

• Использование нейтрального значение

• Ассоциативная операция

Когда мы готовили массив для построения дерева мы заполняли его нулями, но это неправильно в случае с минимумом. Потому что нули это очень маленькие числа и они влияют на итоговый результат. Поэтому необходимо использовать нейтральное значение. То есть значение, которое не влияет на результат. Для минимума, например, можно взять это значение, как INT_MAX. В коде я вынес нейтральное значение в отдельную переменную.

int NEUTRAL = INT_MAX;
void resize(vector<int> &arr) {  
	int s = (int) arr.size();  
	int new_s = (int) pow(2, ceil(log2(s)));  
	arr.resize(new_s, NEUTRAL);  
}

А что же делать с плюсом в дереве сегментов. Все просто: мы можем поменять плюс везде, где он использовался на любую ассоциативную операцию. Я поменял плюс на знак ◾, который будет обозначать любую ассоциативную операцию.
Построение дерева теперь выглядит так.

void build(vector<int> &arr, int v, int tl, int tr) {  
    if (tl == tr - 1) {  
	    t[v] = arr[tl];  
    } else {  
	    int tm = (tl + tr) / 2;  
	    build(arr, v * 2 + 1, tl, tm);  
	    build(arr, v * 2 + 2, tm, tr);  
	    t[v] = t[v * 2 + 1] ◾ t[v * 2 + 2];  
    }  
}

Изменение элемента

void set(int i, int v, int x, int xl, int xr) {  
	if (xl == xr - 1) {  
		t[x] = v;  
		return;  
	}  
	int xm = (xl + xr) / 2;  
	if (i < xm) {  
		set(i, v, 2 * x + 1, xl, xm);  
	} else {  
		set(i, v, 2 * x + 2, xm, xr);  
	}  
	t[x] = t[2 * x + 1] ◾ t[2 * x + 2];  
}

Поиск на отрезке

long long sum(int l, int r, int x, int xl, int xr) {  
	if (r <= xl || l >= xr) {  
		return NEUTRAL; // обратите внимание, тут тоже нейтральное значение
	}  
	if (xl >= l && xr <= r) {  
		return t[x];  
	}  
	int xm = (xl + xr) / 2;  
	return sum(l, r, 2 * x + 1, xl, xm) ◾ sum(l, r, 2 * x + 2, xm, xr);  
}

Четвертая задача

Оригинальное условие задачи
Теперь измените код дерева отрезков, чтобы кроме минимума на отрезке считалось также и число элементов, равных минимуму

То есть
Дан массив arr целых чисел размером n. Необходимо выполнить m запросов. Каждый запрос выглядит так:

• mmin(l,r) - необходимо найти минимум , а также число элементов, равных минимуму на отрезке от l до r - 1

• set(i, v) - меняет значение у элемента arr[i] на v

Для решения такой задачи будем хранить пару чисел в дереве отрезков. Первое число - это само минимальное значение. А второе это количество элементов на отрезке, равных минимальному.

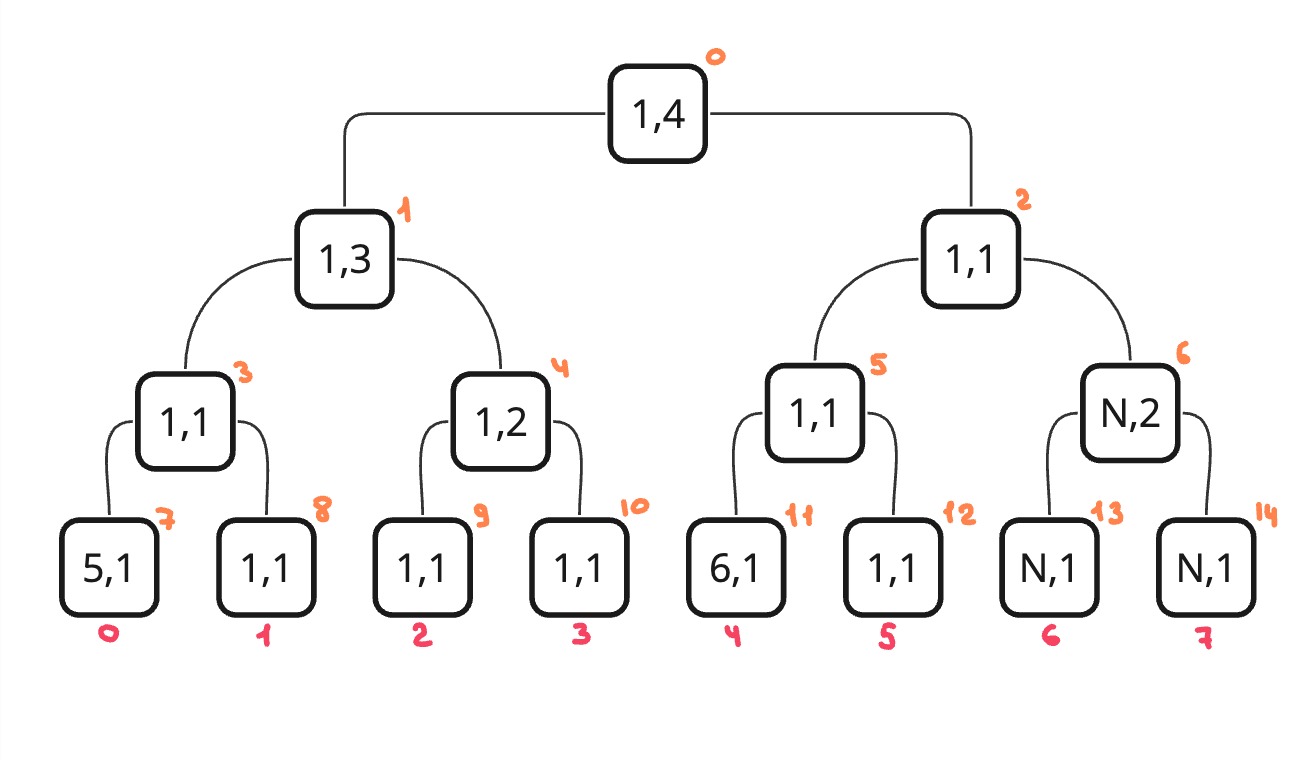
Тогда нам нужно определить нашу ассоциативную операцию. Она будет принимать две пары. Проверяем, если минимальный элемент первой пары меньше мин. элемента второй пары, то возвращаем первую пару. Если наоборот, то вторую пару. Если они равны, то нам нужно вернуть новую пару и сложить количество между собой.

typedef pair<long long, int> Type;
Type combine(Type a, Type b) {  
	if (a.first < b.first) return a;  
	if (b.first < a.first) return b;  
	return {a.first, a.second + b.second};  
}

Теперь мы можем использовать эту ассоциативную операцию вместо ◾ из третьей задачи. Также не стоит забывать про NEUTRAL, который в данном случае можно взять как LLONG_MAX, а второе значение в паре (NEUTRAL будет парой) будет 0, так как для сложения оно является нейтральным значением.

Полное решение можно посмотреть на GitHub

Пятая задача

Оригинальное условие задачи
В этой задаче вам нужно добавить в дерево отрезков операцию нахождения k-й единицы

Особенность такой задачи в том, что оригинальный массив состоит только из 1 или 0. А операция изменения принимает только индекс и меняет значение на противоположное. То есть set(i) -> arr[i] = arr[i] == 1 ? 0 : 1.

Для решения такой задачи будем хранить в узлах количество единиц в отрезке. Тогда операция построения дерева, а также изменения будут такими же как в обычном дереве отрезков. Ассоциативной операцией будет сумма.

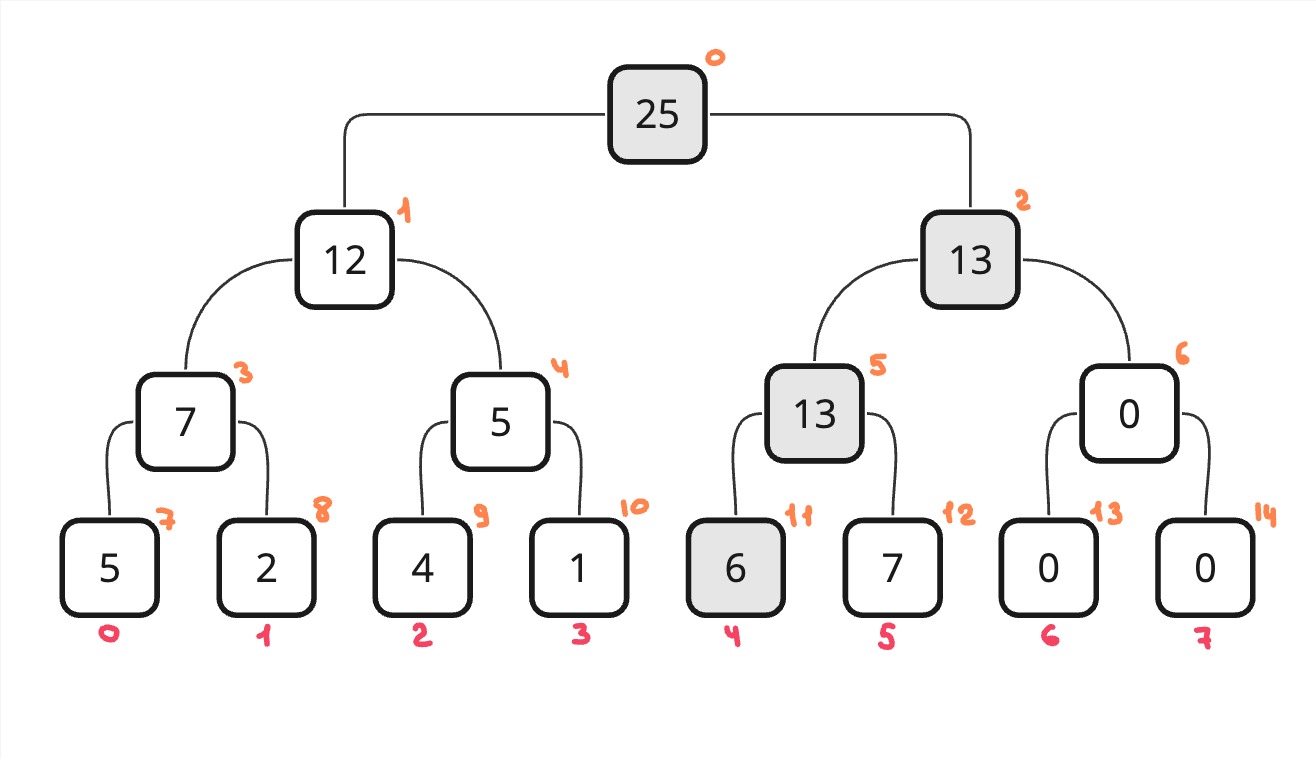
А вот поиск k-ой единицы будет такой: мы опять будем спускаться вниз и проверять левого и правого ребенка. Если искомое k лежит в левом ребенке, то значит нам надо спуститься в левого ребенка. Иначе нужно спускаться в правого ребенка. Когда мы спускаемся в правого ребенка, то нам необходимо уменьшить k на значение из левого ребенка.

Допустим мы ищем k = 2, начинаем с корня. У корня у нас левый ребенок равен 3 и правый тоже равен 3. Это значит, что в левом отрезке у нас есть три единицы, справа также. Нам же нужно получить вторую единицу по порядку. Слева есть три единицы, значит вторая единица будет находится именно там, поэтому спускаемся влево. Далее у нас получаются левый отрезок с одной единицей и правый отрезок с двумя единицами. Левый отрезок нам не подходит, потому что нам нужно две единицы, а слева всего одна единица, поэтому идем вправо. Но тут важно мы правый отрезок ничего не знает про то, сколько единиц было слево от него, именно поэтому нужно уменьшить k на количество единиц слева.

int kith(int k, int x, int xl, int xr) {  
  if (xl == xr - 1) return xl;  
  int xm = (xl + xr) / 2; 
  // идем влево, если слева искомое количество единиц 
  if (t[x * 2 + 1] >= k) {  
    return kith(k, x * 2 + 1, xl, xm);  
  } else {
	// уменьшаем k, потому что слева уже были какие-то единицы
    return kith(k - t[x * 2 + 1], x * 2 + 2, xm, xr);  
  }  
}

Полное решение можно посмотреть на GitHub

Шестая задача

Оригинальная задача
В этой задаче вам нужно добавить в дерево отрезков операцию нахождения по данным x и l минимального индекса j, для которого j >= l и a[j] >= x. Если такого элемента нет, то нужно вернуть -1

В статье e-maxx указан общий случай, когда есть и правая граница, в своем решение они хранят в каждом узле отсортированный список соответствующий отрезку.

В нашем случае правой границы нет, поэтому для решения этой задачи будем использовать дерево отрезков, которое строится на основе максимума. То есть каждый узел будет хранить максимум потомков.

Алгоритм поиска минимального индекса будет выглядеть так:

• Если текущее значение меньше искомого x возвращаем -1

• Если мы вышли за границы j >= l, то возвращаем -1

• Если мы сжались до одного элемента, то возвращаем его индекс

• Иначе поочередно проверяем левого и правого ребенка и возвращаем результат

int above(int v, int l, int x, int lx, int rx) {  
  if (t[x] < v)  
    return -1;  
  if (rx <= l)  
    return -1;  
  if (rx == lx + 1) {  
    return lx;  
  }  
  int m = (lx + rx) / 2;  
  int res = above(v, l, 2 * x + 1, lx, m);  
  if (res == -1) {  
    res = above(v, l, 2 * x + 2, m, rx);  
  }  
  return res;  
}

Разберем на пример, когда нам нужно найти минимальный индекс j, такой что j >= 0 и arr[j] >= 3. На рисунке ниже фиолетовым я указал результат функции для каждого узла. При этом я написал вычисленные значения для каждого узла, хотя на деле значение будет вычислено только для узлов с индексом (оранжевое число) - 0, 1, 3, 7, 8, потому что перед тем, как вычислять правый, мы вычисляем левый и если он равен -1, то только в таком случае вычисляем правый. Схема такая: если слева уже есть какой-то индекс, подходящий нам, то нам уже в принципе не нужна правая часть, потому что она точно будет больше, чем индекс, который вернулся слева.

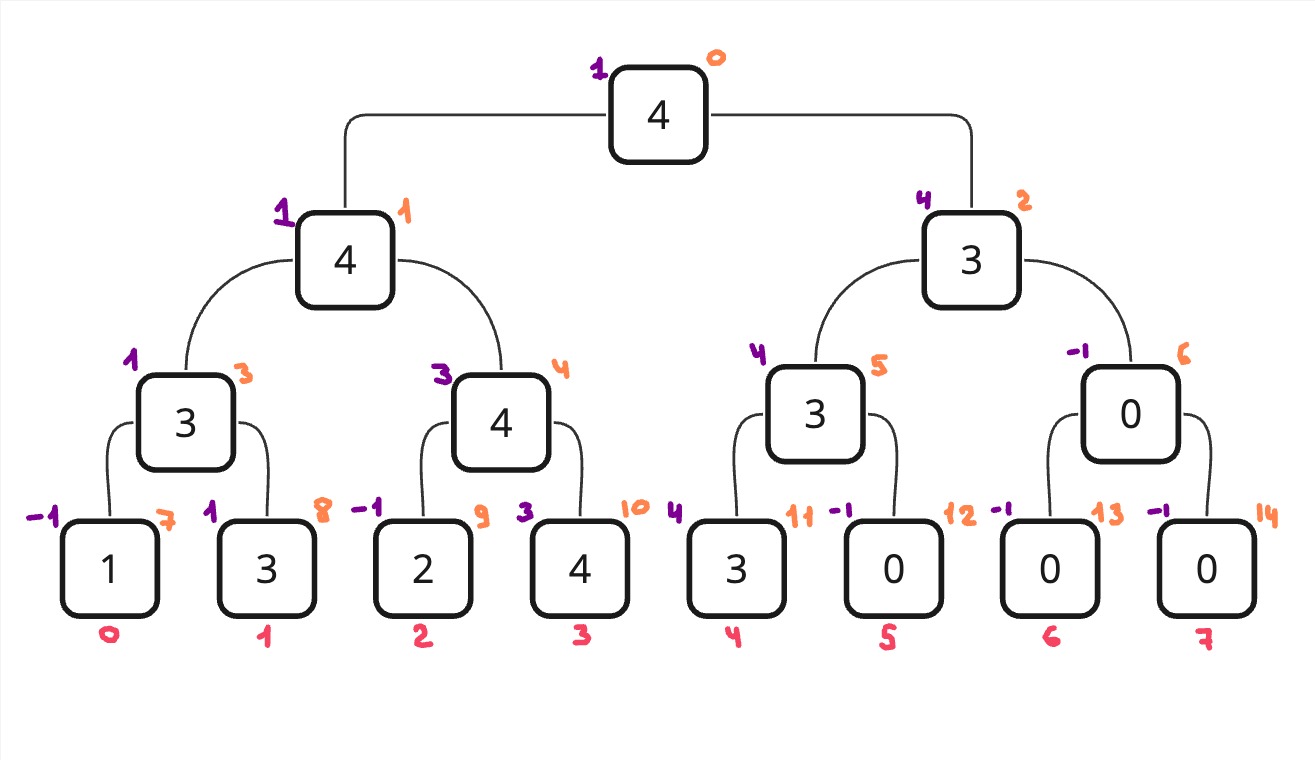
Полное решение можно посмотреть на GitHub

Дерево Фенвика

или Двоичное индексированное дерево было впервые описано российским ученым-математиком Б. Я. Рябко в 1989 году. В 1994 году появилась статья П. Фенвика, где была описана та же структура, которую впоследствии назвали Деревом Фенвика

Вспомним вторую задачу
Дан массив arr целых чисел размером n. Необходимо выполнить m запросов. Каждый запрос выглядит так:

• sum(l,r) - необходимо найти сумму отрезка от l до r - 1 и вернуть ее. Формально: sum(l,r) = a[l] + a[l + 1] + ... + a[r - 1]

• inc(i, v) - добавляет v к значение у элемента arr[i]. По сути замену можно преобразовать в добавление.

Дерево Фенвика работает за O(logn). Но есть ряд особенности

• Писать дерево Фенвика проще

• Работает чуть быстрее, потому что константы меньше

• Занимает меньше памяти, чем дерево отрезков. Лучший вариант дерева отрезков использует O(2n) памяти. Дерево фенвика же хранит один массив длиной n.

Разберем идею по порядку
Пусть у нас будет массив f длиной n, где каждый элемент массива будет суммой на каком-то отрезке, то есть f[i] = Σ arr[p(i) ... i]. То есть условно нам дан какой-то i, мы с помощью функции p(i) получаем левую границу отрезка и заносим в f[i] сумму элементов от левой границы (p(i)) до правой (i)

Как будем вычислять сумму от l до r - 1. Как мы это делали в первой задаче, то есть с помощью префиксных сумм:
sum(l, r) = sum(0, r) - sum(0, l)

Упростим и сделаем, что sum(r) = sum(0, r). Как мы будем вычислять sum(r) - то есть сумму всех элементов до r - 1

int sum(int r) {  
  int i = r - 1;  
  int res = 0;  
  while (i >= 0) {  
    res += f[i];  
    i = p(i) - 1;  
  }  
  return res;  
}

Наглядно можно посмотреть ниже. Функцию p(i) определим попозже, для наглядности я решил, что p(6) = 4

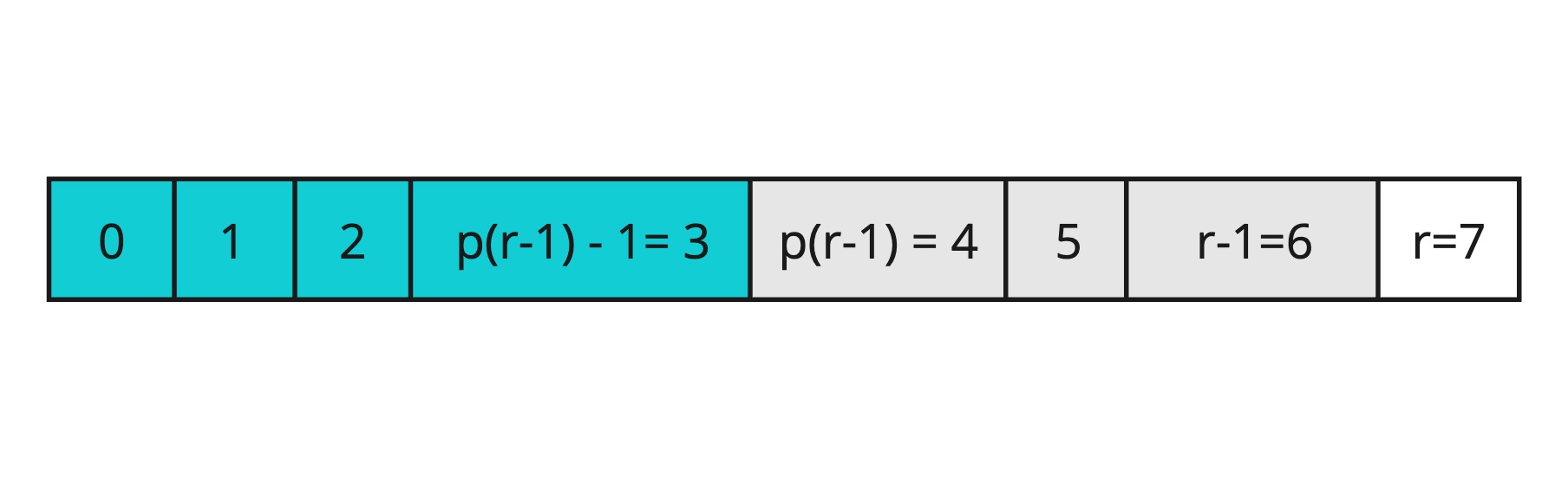
Как выполнить функцию inc(i, v)? Для этого нужно найти все индексы массива f в которые попадает i и прибавить к ним значение v. Разберемся как это делать быстро дальше по тексту.

Как определить функцию p(i)?
Возьмем двоичное представление числа i - ......011111
И заменим все единицы последнего нуля на 0 - ......000000
В таком случае для каждого четного числа p(i) будет равен самому этому числу. А для нечетных будет образовываться закономерность. Функцию можно определить так: p(i) = i & (i + 1)

Функция sum не меняется, мы просто определили функцию p(i). А функция inc(i, v) теперь мы можем определить. Нам дано i и нам нужны все такие индексы j, что i ∊ [p(j), j]
Допустим нам у нас есть двоичное значение
j = .....0111
i = .....0???
p(j) = .....0000

i лежит между j и p(j). Теперь обратное, нам дано i, нам надо найти все j. По сути нам нужно пройтись последовательно по всем нулям в i и менять их на единицу. То есть j | (j + 1)

Наглядный пример:
i = 01010
j = 01010
01011
01111
11111

Код выглядит так:

void inc(int i, int v) {  
  int j = i;  
  while (j < f.size()) {  
    f[j] += v;  
    j = j | (j + 1);  
  }  
}

Вот и все, дерево Фенвика готово. К сожалению дерево Фенвика нельзя использовать для необратных операций, как например, для сумм мы использовали sum(0,r) - sum(0,l). Полная реализация дерева Фенвика:

int n;
int a[100000];  //массив
int f[100000];  //дерево Фенвика

int sum(int x) {
    int result = 0;
    for (; x >= 0; x = (x & (x + 1)) - 1) {
        result += f[x];
    }
    return result;
}

int sum(int l, int r) {
    if (l) return sum(r) - sum(l - 1);
	else return sum(r);
}

void increase(int idx, int delta) {
    a[idx] += delta;
    for (; idx < n; idx |= idx + 1) {
        f[idx] += delta;
    }
}

Седьмая задача

Условие
Дан массив arr целых чисел размером n. Необходимо выполнить m запросов. Каждый запрос выглядит так:

• max(i) - найти максимум среди элементов от 0 до i

• inc(i, v) - увеличить значение по индексу i на v

• set(i, v) - установить значение по индексу i на v. Причем v >= arr[i]

Такая задача называется поиск максимума на префиксе. Дерево Фенвика не может искать максимум на произвольном отрезке, только на префиксе. Код очень похож на стандартное дерево Фенвика, чуть чуть отличаются детали: в этой задаче f[i] будет хранить максимум на отрезке arr[p(i) ... i]

class fenwick {  
public:  
  explicit fenwick(vector<int> &arr) {  
    n = (int) arr.size();  
    a = arr;  
    f.resize(n, 0);  
    for (int i = 0; i < arr.size(); ++i) {  
      set(i, arr[i]);  
    }  
  }  
  
  int mx(int i) {  
    int res = INT_MIN;  
    for (; i >= 0; i = (i & (i + 1)) - 1) {  
      res = max(res, f[i]);  
    }  
    return res;  
  }  
  
  
  void inc(int i, int v) {  
    a[i] += v;  
    for (; i < n; i |= i + 1) {  
      f[i] += v;  
    }  
  }  
  
  void set(int i, int v) {  
    a[i] = v;  
    for (; i < n; i |= i + 1) {  
      f[i] = max(f[i], v);  
    }  
  }  
  
private:  
  vector<int> f;  
  vector<int> a;  
  int n;  
};

Восьмая задача

Условие
Дан массив arr целых чисел размером n. Необходимо удалить из него минимальное число элементов так, чтобы оставшиеся составляли возрастающую последовательность.

Пример: Дан массив 6,2,5,4,2,5,6, если удалить индексы 0, 2, 4, то получится последовательность 2,4,5,6 - которая возрастает и имеет наибольшую длину.

Казалось бы причем тут дерево отрезков или дерево Фенвика. Но давайте потихоньку разберемся как такое быстро (за O(nlogn)) решать.

Динамическое программирование. O(n^2)
Будем хранить в массиве d значения, d[i] равен длине наибольшей возрастающей подпоследовательности, которая оканчивается в arr[i]
Для примера массив d будет равен
a = 6,2,5,4,2,5,6
d = 1,1,2,2,1,3,4

На каждой итерации у нас есть выбор, либо мы запускаем новую подпоследовательность, либо присоединяемся к какой-нибудь подпоследовательности слева. То есть d[i] = max(1, max(d[j]) + 1) при условии, что 0 <= j < i и a[j] < a[i]

Так как подпоследовательность необязательно заканчивается в конце, то ответом будет max(d)

int a[100000];
int d[100000];

int main() {
    for (int i = 0; i < n; i++) {
        d[i] = 1;
        for (int j = 0; j < i; j++) {
            if (a[j] < a[i]) {
                d[i] = max(d[i], d[j] + 1);
            }
        }
    }
    int ans = *max_element(d, d + n);
}

Нетрудно заметить, что такое решение будет работать за O(n^2)

Вот бы можно было искать максимум на префиксе за O(logn). Стоп, это же и есть седьмая задача, получается можно объединить динамическое программирование и дерево Фенвика

class fenwick {  
public:  
  explicit fenwick() {  
    f.resize(1000001, 0);  
  }  
  
  int mx(int i) {  
    int res = INT_MIN;  
    for (; i >= 0; i = (i & (i + 1)) - 1) {  
      res = max(res, f[i]);  
    }  
    return res;  
  }  
  
  void set(int i, int v) {  
    for (; i < 100000; i |= i + 1) {  
      f[i] = max(f[i], v);  
    }  
  }  
  
private:  
  vector<int> f;  
};  
  
int main() {  
  ios::sync_with_stdio(false);  
  cin.tie(nullptr);  
  cout.tie(nullptr);  
  int n;  
  cin >> n;  
  vector<int> arr(n);  
  for (int i = 0; i < n; ++i) cin >> arr[i];  
  
  fenwick tree;  
  for (int i = 0; i < n; ++i) {  
    int q = tree.mx(arr[i]);  
    tree.set(arr[i], q + 1);  
  }  
  cout << tree.mx(100000);  
  return 0;  
}

Если элемент в оригинальном массиве <= 10^6, то можно решать без проблем, иначе нужно будет сжать значения.
Что значит сжать значение. Допустим нам дан массив длиной 10^6, но при этом сами числа в массиве могут быть от -10^9 до 10^9. То есть в целом значение имеет 10^18 вариантов значений, что уже не подходит для дерева Фенвика. Поэтому значения нужно сжать. Как это можно сделать. Так как количество элементов у нас ограничено, то мы можем определить биекцию между реальным элементов и его индексом. Причем два одинаковых элемента должны возвращать один и тот индекс. Таким образом даже в худшем случае, когда все числа уникальны, то получившиеся индексы не превысят 10^6, что подходит для использования в Дереве Фенвика.

Еще раз, теперь наш индекс в дереве Фенвика - это значение. Мы можем быстро найти максимум в отрезке от 0 до i. Более наглядно (d - это обычное динамическое программирование):
a = 6,2,5,4,2,5,6
d = 1,1,2,2,1,3,4
f = 0,0,1,0,2,3,4,0,0....

Мы пробегаемся по всем элементам массива и делаем две операции:

• Находим максимальное значение, которое было до этого значения

• Меняем текущее значение на полученное максимальное + 1

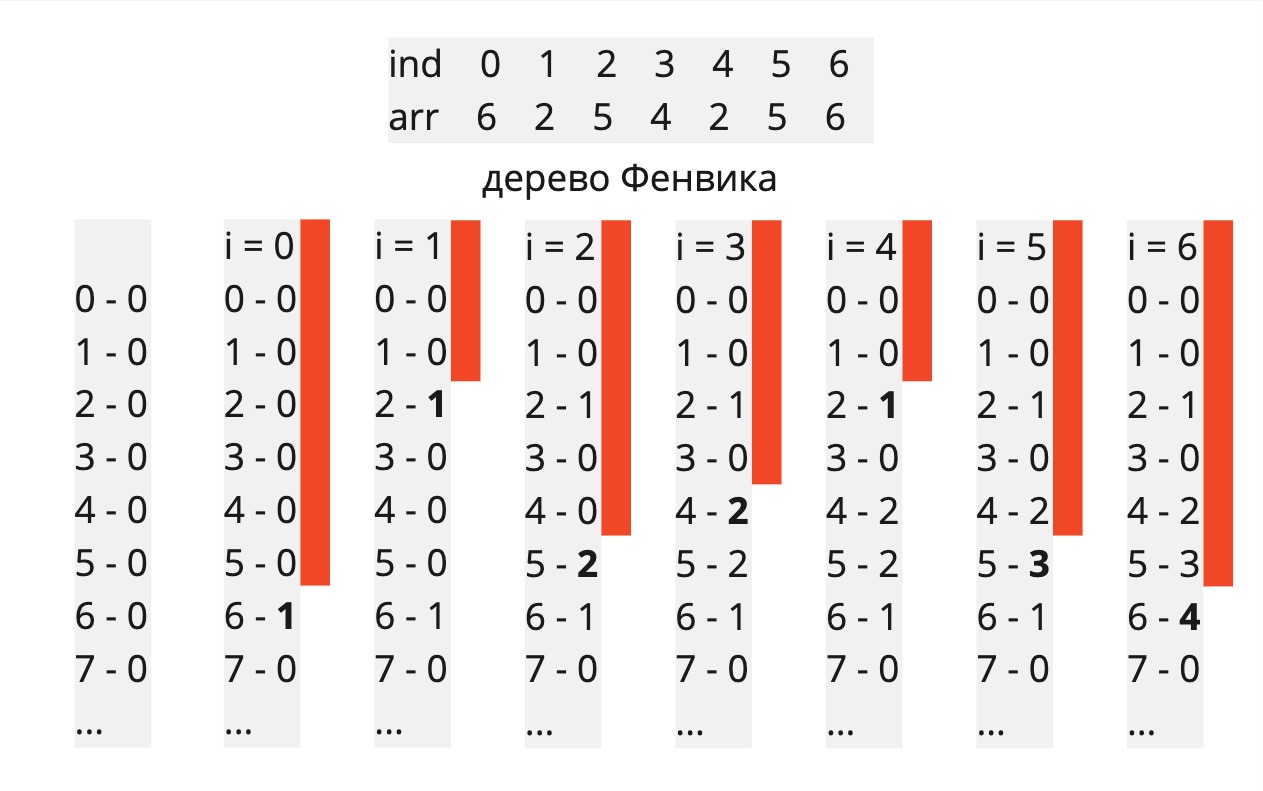
Важная ремарка, на деле массив дерева Фенвика выглядит по-другому, потому что изменяется не только один индекс, но и несколько связанных с помощью функции p(i) индексов, но для упрощения я нарисовал такой вариант.

Девятая задача

Оригинальное условие
Задана последовательность из n чисел. Необходимо найти число возрастающих подпоследовательностей наибольшей длины заданной последовательности a1, . . . , an. Так как это число может быть достаточно большим, необходимо найти остаток от его деления на 10^9 + 7.

Такое же задание можно найти и на LeetCode под номером 673

Решение аналогичному восьмой задачи, но мы будем хранить не только длину, но и количество возрастающих подпоследовательностей.

Полное решение можно посмотреть на GitHub

Здесь мы, кстати, сжимаем числа, так как дерево фенвика не умеет работать с отрицательными индексами.

Десятая задача

Условие
Дан массив из n элементов. Требуется найти в нём количество инверсий. Инверсия это такие индексы i и j, что i < j и arr[i] > arr[j]

Для решения этого задания воспользуемся деревом фенвика на сумму. При каждой итерации мы будем получать количество элементов (сумма), которые находятся правее от текущего числа. Как это работает?

В определенный момент времени (при индексе j) у нас в дереве были добавлены элементы у которых индекс меньше, чем j. Остается только найти количество элементов, которые больше arr[j]. Именно это и написано в условие задачи.

Код выглядит примерно так, но тут важно, что если числа превышают 10^6 их нужно будет сжать.

class fenwick {  
public:  
  vector<int> f;  
  
  explicit fenwick() {  
    f.resize(1000001, 0);  
  }  
  
  int sm(int x) {  
    int result = 0;  
    for (; x >= 0; x = (x & (x + 1)) - 1) {  
      result += f[x];  
    }  
    return result;  
  }  
  
  int sum(int l, int r) {  
    if (l) return sm(r) - sm(l - 1);  
    else return sm(r);  
  }  
  
  void inc(int i) {  
    for (; i < 1000001; i |= i + 1) {  
      f[i]++;  
    }  
  }  
  
};  
  
int main() {  
  int n;  
  cin >> n;  
  vector<int> arr(n);  
  for (int i = 0; i < n; ++i) cin >> arr[i];  
  
  fenwick tree;  
  int ans = 0;  
  for (int i : arr) {  
    auto q = tree.sum(i + 1, 1000000);  
    ans += q;  
    tree.inc(i);  
  }  
  cout << ans;  
  return 0;  
}

Одиннадцатая задача

Оригинальное условие
Римляне снова наступают. На этот раз их гораздо больше, чем персов, но Шапур готов победить их. Он говорит: «Лев никогда не испугается сотни овец».
Не смотря на это, Шапур должен найти слабость римской армии, чтобы победить ее. Как вы помните, Шапур – математик, поэтому он определяет, насколько слаба армия, как число – степень слабости.
Шапур считает, что степень слабости армии равна количеству таких троек i, j, k, что i < j < k и a[i] > a[j]> a[k], где a[x] – сила человека, стоящего в строю на месте с номером x.
Помогите Шапуру узнать, насколько слаба армия римлян.

Переформулировка
Дан массив целых чисел размером n. Необходимо найти количество троек индексов i, j, k, таких, что i < j < k и a[i] > a[j]> a[k]

Обобщение
Дан массив целых чисел размером n. Необходимо найти количество суперинверсий размера k. То есть то же самое, что и с тройками, но вместо трех может быть k

Задача очень похожа на десятую задачу. Идея в том, что если мы знаем сколько двух-инверсий было правее текущего числа, то мы можем узнать количество трех-инверсий. С точки зрения динамического программирования это будет выглядеть так:
a = 6 4 5 1
2_i = 0 1 1 3
3_i = 0 0 0 2
где 2_i - это массив, где 2_i[j] - это количество двух-инверсий, которые оканчиваются в этом индексе. 3_i аналогично, но уже трех-инверсий.

Массив 3_i строится на основе 2_i, 2_i строится на основе a. По сути на каждой итерации в каждом массиве мы ищем количество элементов, которые являются больше текущего. Например 2_i[3] - это количество элементов, которые больше a[3], но которые находятся левее 3 по индексу. А 3_i[3] - это количество элементов, которые больше a[3] и у которых 2_i[j] больше нуля.

По сути при каждой итерации необходимо искать количество элементов, которые больше a[i]. Если решать через динамическое программирование у нас получается сложность O(kn^2), так как мы k раз вычисляем целый массив динамики, а на каждой итерации проходимся с 0 до i. Это можно решить с помощью дерева Фенвика с аналогичной десятой задачи идеей. Просто в этом случае нам нужно будет использовать не одно дерево, а k деревьев.

Решение оригинальной задачи можно посмотреть на GitHub

Двенадцатая задача

Условие
Дан массив arr целых чисел размером n. Необходимо выполнить m запросов. Каждый запрос выглядит так:

• min(l,r) - необходимо найти минимум на отрезке от l до r - 1 и вернуть ее. Формально: `min(l,r) = min(a[l], a[l + 1], ..., a[r - 1])

Заметьте, здесь нет операций изменения массива. Такие задачи решаются двумя частями. Первой - это препроцессинг, когда данные специальным образом подготавливаются. Второй - сами ответы на запросы.

Возможные решения:

• Без подготовки

  • Сложность подготовки - O(1), ничего не делаем

  • Сложность запроса - O(n), в худшем случае пройдемся по всем элемента

• Дерево отрезков

  • Подготовка - O(n)

  • Запрос - O(logn)

• Перебор всех вариантов

  • Подготовка - O(n^2), просто переберем всевозможные отрезки и вычислим для них минимум

  • Запрос - O(1), вернем заранее заготовленные данные

• Разреженные таблицы

  • Подготовка - O(nlogn)

  • Запрос - O(1)

• Алгоритм Фарака-Колтона и Бендера

  • Подготовка - O(n)

  • Запрос - O(1)

Разреженные таблицы

Будем искать минимум для отрезков, но не всех, а только для тех отрезков, у которых длина - это степень двойки. То есть условно у нас будет двумерный массив m, где m[i][k] = min(a[i...i+2^k-1])

Как вычислить значения для такого массива.

• При k = 0 значение m[i][0] = a[i]

• При переходе от k до k + 1: m[i][k + 1] = min(m[i][k], m[i + 2^k][k])

Как теперь найти минимум на отрезке [l, r):
Заметим, что у любого отрезка имеется два отрезка длины степени двойки, которые пересекаются, и, главное, покрывают его и только его целиком. Значит, мы можем просто взять минимум из значений, которые соответствуют этим отрезкам.

Код выглядит примерно так. Здесь используется функция __lg, которая возвращает количество нулей до первой единицы в бинарной записи числа. Код взят с сайта алгоритмики

int a[maxn], mn[logn][maxn];

int rmq(int l, int r) { 
    int t = __lg(r - l);
    return min(mn[t][l], mn[t][r - (1 << t)]);
}


memcpy(mn[0], a, sizeof a);

for (int l = 0; l < logn - 1; l++)
    for (int i = 0; i + (2 << l) <= n; i++)
        mn[l+1][i] = min(mn[l][i], mn[l][i + (1 << l)]);

Тринадцатая задача

Дан массив arr целых чисел размером n. Необходимо выполнить m запросов. Каждый запрос выглядит так:

• add(l, r, v) - нужно добавить всем элемент в отрезке от l до r - 1 элемент v

• get(i) - нужно получить i элемент

Построим дерево отрезков для этой задачи. Теперь каждый узел будет хранить значение, которое нужно добавить к отрезку, к которому относится этот узел.

Для выполнения добавления, необходимо разделить нашу границу на части и добавить в узлы, относящиеся к этим отрезкам значение v. А для получения i элемента необходимо пройти весь путь от корня до вершины i и собрать ответ, сложив значения.

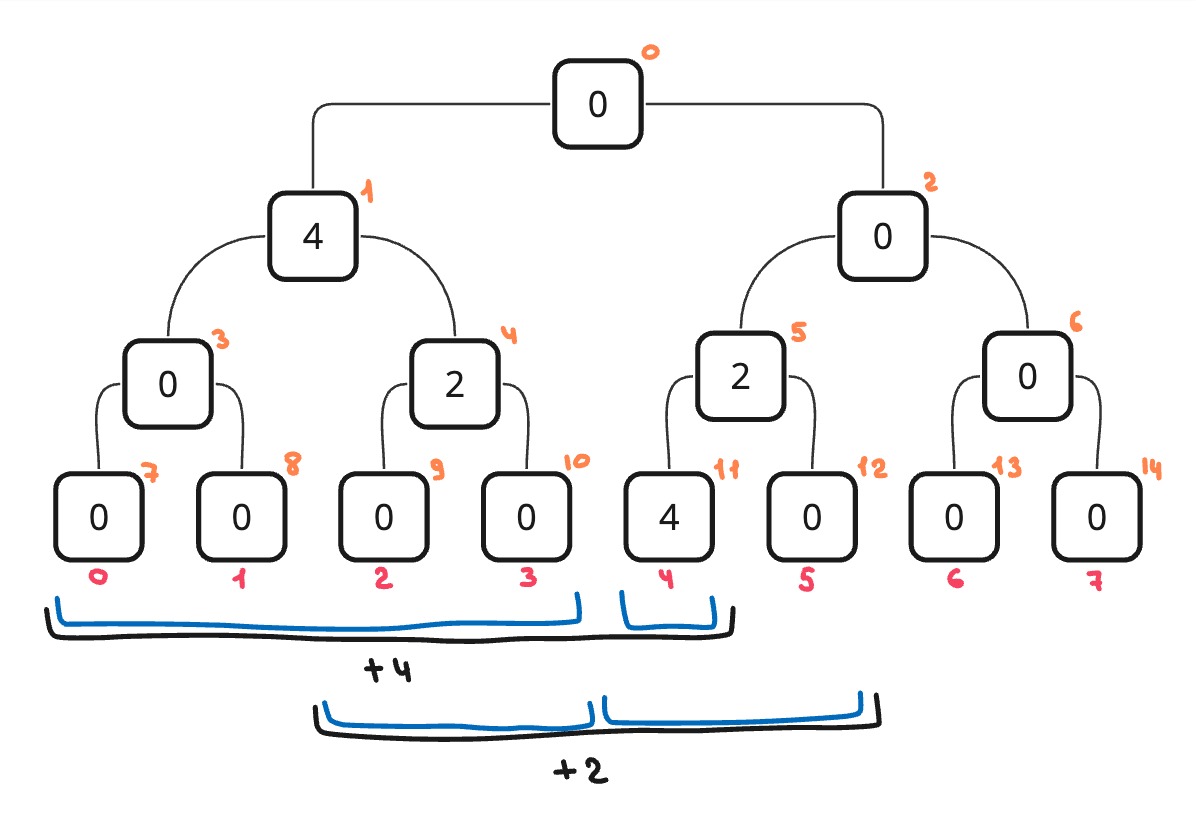
void resize(vector<int> &arr) {  
  int s = (int) arr.size();  
  int new_s = (int) pow(2, ceil(log2(s)));  
  arr.resize(new_s, 0);  
}  
  
vector<int> t;  
  
void init(vector<int> &arr) {  
  resize(arr);  
  t.resize(arr.size() * 2, 0);  
}  
  
void add(int l, int r, int v, int x, int xl, int xr) {  
  if (l >= xr || xl >= r) {  
    return;  
  }  
  if (xl >= l && xr <= r) {  
    t[x] += v;  
    return;  
  }  
  int xm = (xl + xr) / 2;  
  add(l, r, v, 2 * x + 1, xl, xm);  
  add(l, r, v, 2 * x + 2, xm, xr);  
}  
  
int get(int i, int x, int xl, int xr) {  
  if (xl == xr - 1) {  
    return t[xl];  
  }  
  int xm = (xl + xr) / 2;  
  if (xm > i) {  
    return t[x] + get(i, 2 * x + 1, xl, xm);  
  } else {  
    return t[x] + get(i, 2 * x + 2, xm, xr);  
  }  
}

Здесь могли быть еще задачи...

С помощью дерева отрезков можно в одной задачи объединять сразу несколько операций, например, присвоение и добавление на отрезке и поиск максимума. Или XOR или OR и что-то еще. Также можно решать двумерные задачи с помощью дерева отрезков. Но такие темы не очень приятно расписывать, да и они выходят за базовое понимание дерева отрезков. Посмотреть еще несколько задач на двумерные и множественные операции на дереве отрезков можно на GitHub

Вот и все, надеюсь, что статья принесла кому-нибудь пользу ?