WebGPU — это мощный GPU-API для веба, поддерживает продвинутые рендеринговые конвейеры и вычислительные конвейеры GPU. WebGPU ключевым образом отличается от WebGL своей поддержкой вычислительных шейдеров и буферов хранения данных. В WebGL такие возможности отсутствуют, а WebGPU, в свою очередь, позволяет целиком выполнять в браузере мощные приложения, требующие вычислений на GPU. Речь может идти о самых разных приложениях, от GPGPU (напр., симуляции, обработка/анализ данных, машинное обучение, т.д.) до конвейеров рендеринга на основе GPU-вычислений — а также о многих других приложениях в этом спектре.

В этой статье мы оценим вычислительную мощность WebGPU, сравнив её с показателями Vulkan. Для этого мы реализуем классический алгоритм «марширующие кубы» (Marching Cubes) для WebGPU. Алгоритм марширующих кубов почти без оговорок относится к чрезвычайно параллельным, в составе этого алгоритма выполняется два глобальных шага редукции, необходимых для синхронизации местоположений рабочих элементов и вывода потоков. Поэтому данное решение — отличный вариант GPU-параллельного алгоритма, который стоит первым делом попробовать на новой платформе. Дело в том, что он достаточно сложен, чтобы API испытал давление сразу по нескольким направлениям сверх элементарных параллельных операций диспетчеризации в ядре. При этом он не столь сложен, чтобы на его реализацию требовалось существенное время, а также он не превращается в узкое место из-за ограничения производительности ЦП.

Хотя, в этой статье мы сосредоточимся на стандартной GPU-параллельной реализации марширующих кубов, давайте для начала подробнее разберёмся, как именно обрабатываются данные в соответствии с этим алгоритмом. Также попробуем рассмотреть взаимозависимости внутри алгоритма (если таковые найдутся), чтобы посмотреть, как его можно распараллелить. Более подробно алгоритм марширующих кубов и его выполнение в контексте скалярной задачи рассмотрены в отличной статье Пола Бёрка. Ещё одна крутая работа, в которой основы марширующих кубов описаны, начиная со случая на плоскости, находится здесь.

Чтобы сконструировать треугольный меш, представляющий целую поверхность, алгоритм марширующих кубов сводит проблему к задаче вычисления отдельных участков поверхности, проходящих через каждый воксель. Просматривается ряд возможностей, как именно провести поверхность через воксель. Например, поверхность может разрезать ячейку пополам, отсекать от ячейки угол, проходить через ячейку под углом, либо вообще через неё не проходить. У каждого вокселя   8 вершин, каждая из которых может находиться внутри или извне поверхности. Таким образом, получается всего 2⁸ = 256 возможных конфигураций вокселя. Для каждого вокселя вычисляется 8-разрядная битовая маска, где для каждой вершины, находящейся ниже желаемой поверхности, устанавливается значение 1. Воксельная битовая маска применяется для индексирования при составлении таблицы триангуляции. В этой таблице хранится список рёбер, пересекающих каждый треугольник на локальной поверхности вокселя. На поверхности каждого вокселя может содержаться до 5 треугольников, что следует из описания случаев триангуляции, приведённых в исходной статье по алгоритму марширующих кубов.

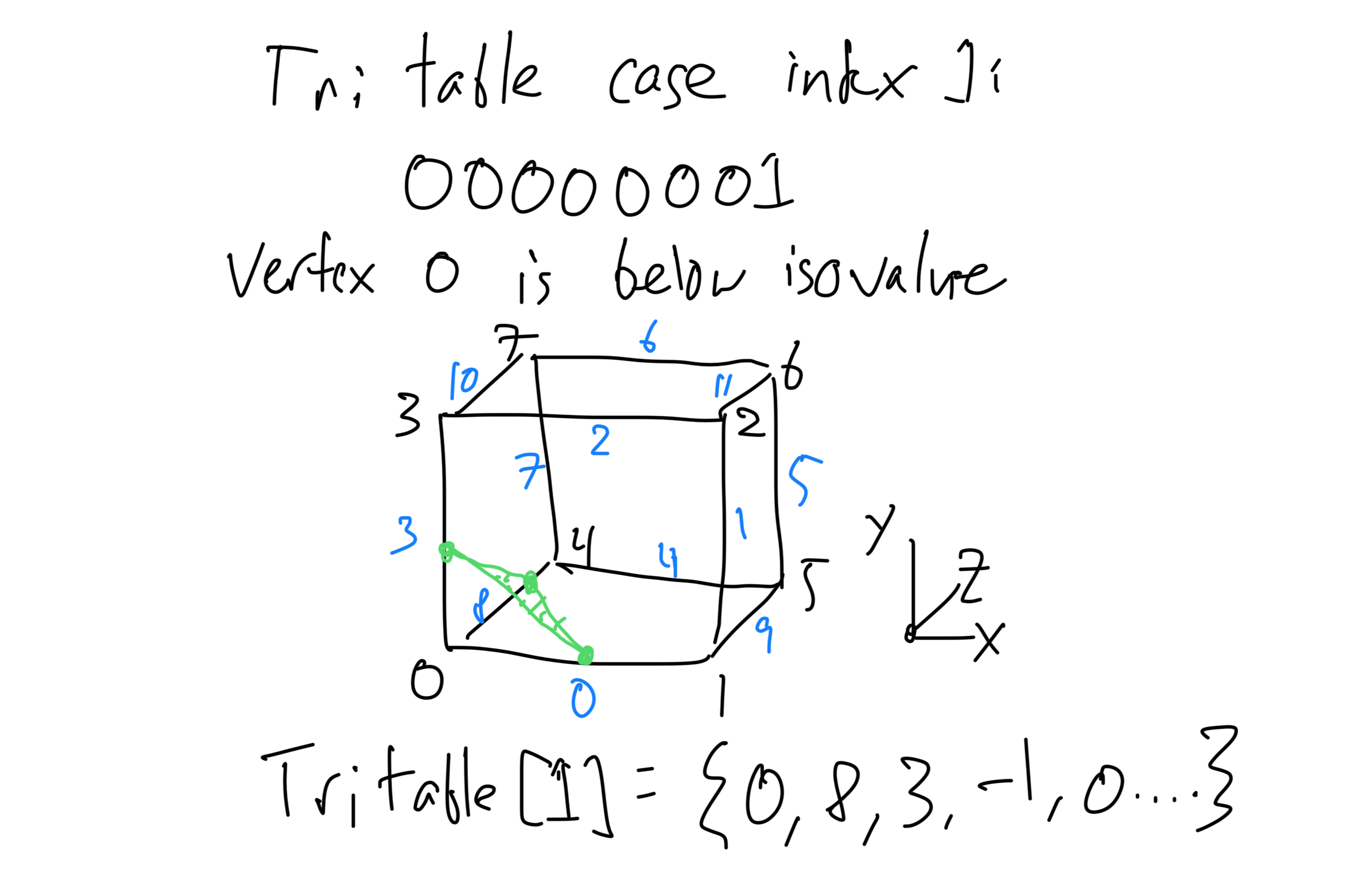
Последовательную версию алгоритма можно реализовать при помощи следующего псевдокода:

output_vertices = []
for v in voxels:
  vertex_values = load_voxel_vertices(v)
  case_index = compute_case_index(vertex_values, isovalue)

  # В этом вокселе треугольников нет, пропускаем его
  if case_index == 0 || case_index == 255:
    continue

  triangulation = case_table[case_index]
  for tri in triangulation:
    vertices = compute_triangle_vertices(tri, vertex_values, isovalue)
    output_vertices += vertices

Работа над двойной сеткой

Алгоритм марширующих кубов требует, чтобы значения каждого вокселя определялись в его вершинах, то есть, сетка должна быть «вершинно-центричной». Но, если мыслить в терминах изображений или объёмов (объёмы, в сущности, являются 3D-изображениями), то оказывается, что они обычно понимаются как ячеечно-центричные, то есть, их значения определяются в центре каждого пикселя или вокселя. Чтобы реализовать марширующие кубы в ячеечно-центричной сетке, перейдём к варианту с «двойной сеткой». В двойной сетке вершины устанавливаются в центрах ячеечно-центричной сетки. Получается второй слой, то есть, вершинно-центричная сетка, которая на ячейку меньше по каждой оси, при этом сдвинутая на половину ячейки:

Распараллеливаем марширующие кубы на GPU

Как видно из вышеприведённого псевдокода, марширующие кубы хорошо подходят для параллельного выполнения, поскольку каждый воксель можно обрабатывать независимо. Но все воксели записывают информацию в один массив, и, если отнестись к ним неаккуратно, то рано или поздно возникнет конфликт при записи. Речь о массиве output_vertices. Каждый воксель может выдавать на выход переменное количество вершин, в зависимости от того, каковы значения вершин. Известно, что каждый воксель может давать на выход максимум 5 треугольников, поэтому можем осторожно выделить пространство под 5 треугольников на воксель, а те записи, что останутся неиспользованными, заполнить вырожденными треугольниками. Правда, в таком случае для работы с крупными поверхностями нам потребуется запредельное количество памяти, и такая работа неизбежно ухудшит качество рендеринга. Вместо этого лучше подавать на выход компактный буфер, в котором содержались бы только полноценные результирующие треугольники.

Чтобы написать компактный буфер вершин, при этом не позволяя вокселям «наступать» на вывод друг друга, распределим процесс триангуляции по двум ядрам. Далее задействуем так называемую «префиксную сумму» (она же — эксклюзивное сканирование), классический примитив параллелизма. Сначала вычисляем, сколько вершин даст нам на выход каждый воксель, а затем методом эксклюзивного сканирования преобразуем этот список в последовательность выходных смещений для каждого вокселя. Наконец, задействуем второе ядро, которое запишет треугольники каждого вокселя в выделенный под них субрегион массива. При этом пользуемся смещениями, вычисленными в ходе эксклюзивного сканирования.

Также применим другую оптимизацию, для которой требуется ещё и шаг глобальной синхронизации. На этом шаге отфильтровывается список тех вокселей, над которым будут работать оба ядра – то, которое подсчитывает вершины, и то, которое выполняет вычисления. Эта оптимизация похожа на более раннюю, показанную в псевдокоде. В контексте параллельных вычислений на GPU для решения этой задачи вычисляется список ID активных вокселей. Главная польза этого шага заключается в том, что мы активнее задействуем GPU и обеспечиваем согласованность в работе ядер, выполняющих вычисления над нашими вершинами. Вместо диспетчеризации тысяч потоков, которые почти сразу же выходят по той причине, что во многих из попавшихся им вокселей не содержится треугольников, можно заранее эффективно отфильтровать нужные вершины. В таком случае вычислительные ядра будут работать лишь со сравнительно небольшим списком активных вокселей. Как правило, изоповерхности очень разреженные, из общего числа вокселей на них могут быть активны всего 4,5%-45% (более подробная статистика приводится в этой статье).

Эксклюзивное сканирование

Воспользуемся классической очень эффективной реализацией параллельного сканирования, описанной для CUDA Харрисом и др. в GPU Gems 3. Текст Харриса и др. просто отличный, а имеющийся перевод на WebGPU и WGSL — это, в сущности, прямой перевод кода CUDA. Поэтому ниже я просто поясню некоторые подробности о том, как именно работает сканирование, и объясню, почему эта техника полезна при распараллеливании алгоритма марширующих кубов на GPU.

Эксклюзивное (и инклюзивное) сканирование образуют общий фундамент алгоритмов для параллельной обработки данных. Например, эту технику обычно применяют для вычисления смещений памяти при параллельной выдаче данных — именно этом нам и требуется в случае с марширующими кубами. Механизм таков: сначала выводим буфер counts, в котором фиксируется, сколько выходных значений приходится на каждое входное. Например, вычислив, сколько треугольников получим на выход для каждого вокселя, можем получить примерно такой буфер, как показан ниже:

counts = [0, 3, 2, 0, 0, 5, 4]

Теперь известно, сколько треугольников мы получим с каждого вокселя, но мы пока не знаем, куда именно записать их в буфере вывода результатов, так, чтобы эти значения не мешали выводу с других вокселей. В помощь нам эксклюзивное сканирование! При эксклюзивном сканировании вычисляется выходная сумма y для ввода x, вот так:

y_0 = 0
y_1 = x_0
y_2 = x_0 + x_1

Применим это к буферу counts и получим:

out = [0, 0, 3, 5, 5, 5, 10]

Чтобы получить общее количество выходных значений, можно увеличить выходной буфер на 1 элемент. В результате получим:

out = [0, 0, 3, 5, 5, 5, 10, 14]

Теперь, учитывая буфер counts, вычисляем, что у нас получается на выходе всего 14 треугольников, на которые мы должны выделить память. Также получаем те адреса, по которым будут находиться результирующие треугольники. Воксель 1 будет записывать со смещением 0, воксель 2 — со смещением 3, воксель 5 — со смещением 5, а воксель 6 — со смещением 10.

Полная реализация данного проекта находится в файле exclusive_scan.ts, а шейдеры — здесь: exclusive_scan_prefix_sum.wgsl, exclusive_scan_prefix_sum_blocks.wgsl и exclusive_scan_add_block_sums.wgsl. В реализации необходимо дробить операции диспетчеризации, чтобы они вписывались в максимальный размер фрагмента для вычисления диспетчеризации, предусмотренный в WebGPU. При этом также должны использоваться динамически подбираемые групповые смещения (bind group) буферов. Это нужно, чтобы открыть шейдерам доступ к нужному субрегиону входного буфера при поблочном его сканировании.

Уплотнение потока

При приведённом выше описании параллельного алгоритма мы просто постулировали следующие операции: задействуем два ядра, на одном из которых подсчитываются треугольники, а на другом выполняются вычисления. Эти операции выполняются над активными вокселями. Но в таком случае ещё нужно позаботиться об уплотнении потока операций, как обычно в контексте параллельной обработки данных. Подобно тому, как нам требуется вычислить буфер адресов, по которым мы будем записывать выходные значения каждого вокселя, мы также должны вычислить и компактный список ID тех вокселей, на которые может приходиться изоповерхность. Такая операция обычно называется «уплотнением потока», где мы имеем множество элементов в качестве входных значений плюс массив масок, при помощи которых указываем, хотим ли мы оставить или отбросить конкретный элемент. В выводе будут содержаться либо сами элементы, либо, как в нашем случае, их индексы. К счастью, такое уплотнение можно осуществить при помощи всё той же операции эксклюзивного сканирования, которую мы обсудили выше.   

Наш буфер масок примет вид:

masks = [1, 0, 0, 1, 1, 0]

Применив эксклюзивное сканирование с масками, получим список тех смещений, под которыми будем записывать уплотнённые результаты, а также общее количество элементов (опять же, смещения на 1 элемент больше, чем в массиве масок).

offsets = [0, 1, 1, 1, 2, 2, 3]

Теперь всё, что осталось сделать — написать ядро, которое обрабатывало бы каждый выходной элемент и записывало его индекс с указанным смещением в случае, если маска этого элемента равна 1!

Можно написать и другую реализацию, при которой более эффективно используется память. В таком случае сканируется непосредственно буфер масок и проверяется, активен ли элемент, вот так:

offset[current] < offset[current + 1]

Значение true свидетельствует, что данный элемент активен, так как для следующих за ним элементов пришлось увеличить результирующее смещение, чтобы освободить место для его вывода.

Реализация уплотнения потока, в которой ID активных вокселей уплотняются на основе данных буфера смещений приведена в файлах stream_compact_ids.ts и stream_compact_ids.wgsl. Реализация именно такая, как описана здесь, но включает ещё некоторые операции обработки, нужные для фрагментации диспетчерских операций при сканировании, когда операция не вписывается в максимальный размер, отведённый под диспетчеризацию.

Собираем всё вместе в WebGPU

Вот мы и реализовали наши примитивы для параллельной обработки данных: эксклюзивное сканирование и уплотнение потока. Теперь мы готовы достроить специфические детали, связанные с алгоритмом марширующих кубов, и реализовать наш параллельный алгоритм. В нём будет три этапа:

1.    Вычисление ID активных вокселей

2.    Вычисление результирующих смещений для вершин

3.    Вычисление вершин

После чего мы сможем отобразить вычисленную поверхность.

Вычисляем ID активных вокселей

Вычисление ID и построение списка активных вокселей, в свою очередь, проходит в три этапа:

1.    Запускаем ядро, чтобы пометить активные воксели и подготовить буфер масок

2.    Подвергаем буфер масок эксклюзивному сканированию, чтобы получить результирующие смещения для активных вокселей

3.    Исходя из смещений, уплотняем ID активных вокселей методом уплотнения потока

Мы реализовали примитивы для шагов 2 и 3. Остаётся только написать ядро для обработки двойной сетки, которое бы вычисляло, активен данный воксель или нет. Ядро получается прямой трансляцией первого бита показанного выше псевдокода, за исключением того, что оно не вызывает continue, а записывает 0 или 1 в буфер масок.

Полный код ядра приведён в файле mark_active_voxel.wgsl, а ниже он записан в сокращённой псевдо-шейдерной форме. Это ядро обрабатывает каждый воксель из двойной сетки и таким образом параллельно выстраивает буфер масок.

float values[8] = compute_voxel_values(voxel_id);
uint case_index = compute_case_index(values, isovalue);
voxel_active[voxel_idx] = case_index != 0 && case_index != 255 ? 1 : 0;

Расчёт числа вершин и их результирующих смещений

Теперь, имея список всех вокселей, которые могут дать на выходе треугольники, можно вычислить, сколько треугольников получится из каждого. Таким образом мы определим результирующие смещения и подсчитаем общее число треугольников. Это делается при помощи ядра compute_num_verts.wgsl, которое параллельно обрабатывает ID активных вокселей и выдаёт, сколько вершин в результате получится из этих вокселей. Поскольку здесь мы не используем индексированного рендеринга, из каждых трёх вершин строится треугольник.

Ядро compute num verts вычисляет, сколько вершин на воксель получается на выходе, это делается при помощи таблицы марширующих кубов. Как было показано в первом наброске с вычислениями для единственного вокселя, в этой таблице определяются те рёбра вокселя, на которых лежат вершины треугольника, а окончание данной последовательности отмечается как -1. Следовательно, наше ядро может загрузить значения вокселей, а затем перебрать значения, содержащиеся в таблице, и таким образом вычислить, сколько вершин мы получим на выходе:

float values[8] = compute_voxel_values(voxel_id);
uint case_index = compute_case_index(values, isovalue);
int triangulation[16] = case_table[case_index];
uint num_verts = 0;
for (uint i = 0; i < 16 && triangulation[i] != -1; ++i) {
    ++num_verts;
}
voxel_num_verts[work_item] = num_verts;

Затем применяем эксклюзивное сканирование к выходному буферу voxel_num_verts и вычисляем результирующие смещения для каждого вокселя, а также узнаём, сколько всего вершин получим на выходе.

Вычисление вершин

Зная результирующие смещения и выделив место под выходной буфер вершин, нам остаётся, собственно, вычислить вершины и вывести их! Это делается при помощи ядра compute_vertices.wgsl. Оно принимает список ID активных вокселей и ранее вычисленные значения результирующих смещений, после чего рассчитывает вершины для каждого вокселя и записывает их в вывод. Это ядро параллельно обрабатывает все активные воксели.

Вершины для каждого вокселя вычисляются перебором соответствующих триангуляций и линейной интерполяцией между вершинами на концах каждого ребра с учётом значения поля. Так вычисляется позиция, в которой изоповерхность пересекает ребро. Вершина сначала рассчитывается для единичного вокселя, затем смещается до позиции этого вокселя в объёмной сетке и ещё на 0,5 в двойной сетке. Ниже этот процесс представлен в псевдо-шейдерном коде, а весь код ядра выложен на Github к этой статье.

float values[8] = compute_voxel_values(voxel_id);
uint case_index = compute_case_index(values, isovalue);
int triangulation[16] = case_table[case_index];
uint output_offset = vertex_offsets[work_item];
for (uint i = 0; i < 16 && triangulation[i] != -1; ++i) {
    // Линейная интерполяция начальной/конечной вершин ребра позволяет найти, где 
    // изоповерхность пересекается с ребром
    uint v0 = edge_start_vertex(triangulation[i]);
    uint v1 = edge_end_vertex(triangulation[i]);
    float t = (isovalue - values[v0]) / (values[v1] - values[v0]);
    vec3 v = lerp(voxel_pos[v0], voxel_pos[v1], t);
    
    // Смещение v на позицию вокселя в двойной сетке и вывод 
    output_vertices[output_offset + i] = v + voxel_pos + 0.5;
}

Отображение поверхности

Чтобы вычислить поверхность, нам пришлось потрудиться и порядком погонять все наши ядра! К счастью, отоборазить её просто. На выходе того этапа, где мы вычисляли вершины, получаем набор треугольников, в котором все вершины для всех вокселей записываются в виде неиндексированного списка треугольников. Его можно представить в обычной топологии «список треугольников», не требующей буфера индексов.

Заключение: сравним производительность WebGPU и Vulkan

Закончив нашу реализацию, проверим, как она смотрится на фоне нативной реализации Vulkan! Я реализовал в Vulkan совершенно аналогичный код, который выложен здесь на Github. Для этих тестов было использовано несколько маленьких датасетов из OpenScivisDatasets, а именно Череп, Бонсай, Ступня и Аневризма. Размер каждого датасета составляет 256x256x256, всего 16,77 млн ячеек (в двойной сетке 16,58 миллионов ячеек).

В обоих методах я выполнил заметание изозначений от 30 до 110, охватив такие изоповерхности, которые могли бы заинтересовать типичного пользователя (т.е., не слишком зашумленные, не слишком мелкие). Ниже приведена таблица с результатами, полученными на MacBook Pro с M2 Max и RTX 3080. Модель RTX 3080 использовалась для сравнения производительности WebGPU и Vulkan. Приходим к выводу, что в целом производительность очень близка к той, что наблюдается в нативной версии Vulkan!

Действительно здорово располагать современным API для работы с GPU прямо в браузере, да ещё к такому, который привносит минимальные издержки. Открывается масса новых возможностей для программирования игр, инструментов подготовки контента, научных приложений и многого другого. Все они работают в браузере и практически не отличаются по производительности от нативных аналогов. В настоящее время такое приложение работает только в Chrome, но Safari и Firefox также активно заняты разработкой WebGPU. Жду того дня, когда поддержкой WebGPU обзаведутся многочисленные вендоры!

Live-демонстрация и код

Код реализации алгоритма марширующих кубов для WebGPU выложен на Github и должен работать в Chrome. Firefox Nightly и Safari Tech Preview на момент подготовки оригинала этой статьи ещё не могут воспроизводить это демо. Вы можете погонять его здесь: https://www.willusher.io/webgpu-marching-cubes/