В этой статье мы постараемся понять, каким образом поиск оптимальных параметров объекта или модели может быть автоматизирован и сведен к оптимизации некоторой ресурсоемкой функции типа «черный ящик». Подробно рассмотрим математический метод (и его реализацию) для эффективного решения этой задачи.

Немного философии

Если не вдаваться в детали, то процесс решения многих инженерных (и не только) задач может быть изображен в виде такой схемы:



Простой пример — проектирование кузова спортивного автомобиля. В данном случае дизайн — это геометрия кузова, модель — некоторый расчетный пакет, а результат — скажем, вычисляемое аэродинамическое сопротивление.

Важно вот что — в приведенной выше схеме один из блоков всегда неизвестен. И это приводит нас к трем фундаментальным задачам:

• Прямая задача (неизвестен результат)
• Построение модели (неизвестна модель)
• Обратная задача (неизвестен дизайн)

Прямая задача принципиально проста. По сути это задача о построении интерфейса — пользователю должно быть удобно задать дизайн и интерпретировать результаты работы программы (подобные интерфейсы уже давно существуют и продолжают совершенствоваться). В то же время построение модели — задача принципиально сложная. Ученый, исходя из наблюдений, понимания и анализа, занимается научным творчеством, которое в общем случае не автоматизируемо, по крайней мере на сегодняшний день.

А вот с обратной задачей все не так однозначно. С одной стороны, процесс создания дизайна также представляет собой творчество. А с другой стороны, дизайн можно представить в виде набора некоторых численных параметров (самых существенных в рассматриваемом контексте), а результат — в виде некоторой численной оценки того, насколько дизайн хорош. Таким образом ищется набор параметров, которые максимизируют/минимизируют некоторую величину, а значит обратная задача — это задача математической оптимизации и ее решение может и должно быть автоматизировано.


И поскольку мы заговорили об оптимизации, нужно понимать с какой функцией мы имеем дело. А функция эта непростая:

• Мы знаем только входящие параметры (input) и, по результатам численного эксперимента, значение скалярной оценки (output). Сама же функция неизвестна, поскольку представляет собой сложную систему. И поэтому проще всего называть ее черным ящиком.
• Эта функция может быть очень ресурсоемкой и занимать минуты, часы и дни для вычисления в одной точке (то есть для одного набора параметров).

Таким образом, для решения обратных задач нам нужно научиться эффективно оптимизировать такие черные ящики (expensive black-box functions). Далее поговорим о математике, которая для этого используется.

Математический принцип

Перед тем, как углубиться в решение, постараемся понять следующее. Главная проблема — это не то, что функция представляет собой черный ящик (не имеет аналитического выражения), а то, что она долго вычисляется. Если бы она вычислялась быстро, то задача ее оптимизации решалась каким-нибудь простым проходом по сетке, методом Монте-Карло, или одним из градиентных методов. Но, учитывая дороговизну функции, и соответственно дороговизну вычисления ее градиента, нужно поступать более экономно.

Поступим так — сначала вычислим функцию в очень небольшом количестве точек, равномерно покрывающих пространство поиска, а затем интерполируем полученные значения некоторой гладкой поверхностью. Таким образом мы как бы реконструируем исходную функцию по значениям в нескольких точках, не вычисляя градиенты. Полученная поверхность укажет нам на наиболее вероятное местоположение оптимума, где мы уже сможем его уточнить.

Начальная выборка

Для простоты будем считать, что каждая переменная нашей функции имеет свой независимый интервал значений. Таким образом пространство поиска представляет собой параллелепипед в многомерном пространстве. Если же нормализовать каждую переменную, то пространство поиска становится единичным кубом (здесь и далее будем опускать приставку «гипер»).

Первый вопрос — как наиболее эффективно (наиболее равномерно) расположить заданное начальное количество точек в пространстве поиска (кубе)?

В одномерном случае, когда функция задана на отрезке, решение очевидно — равномерная сетка. Однако равномерная сетка работает заметно хуже в многомерном случае поскольку количество точек сильно привязано к размерности пространства. Скажем, в четырехмерном пространстве сетка размера 2 образует 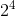(16) точек, в то время как сетка размера 3 образует 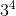(81) точку. При этом, если у нас есть вычислительное время для, допустим, 30 точек, то 16 точек для нас — слишком мало, а 81 — слишком много. И ситуация, очевидно, будет усугубляться с ростом размерности.

Еще один вариант — использовать случайную выборку. В этом случае мы не привязаны к размерности пространства и можем генерировать произвольное количество точек. Однако, возникает другая проблема — неравномерность покрытия. Вот типичное расположение 20 случайных точек в единичном квадрате:



На помощь приходит метод под названием Latin hypercube (LH). Представим, что нужно расставить 8 не бьющих друг друга ладей на шахматной доске — то есть в каждой строке и каждом столбце доски должна быть ровно одна ладья. Это и есть LH, только вместо ладей мы размещаем точки, а доска может быть многомерной и ее размер может быть отличным от 8. Можно показать, что количество точек в этом случае равно размеру доски и не привязано к размерности пространства. При этом существует множество различных LH заданного размера и нас будут интересовать не все подряд, а только те, в которых точки расположены как можно более равномерно. Оказывается, что построить такое расположение можно с помощью довольно простого метода.

Для примера будем размещать 20 точек в квадрате. Сначала расположим точки диагональным образом:



Далее мы выбираем 2 произвольных строки/столбца и меняем их местами. После каждого такого обмена будем следить, чтобы равномерность покрытия возросла. Сделать это можно, определив такую меру:



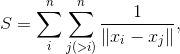
где 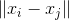— евклидово расстояние между двумя точками, а 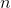— количество точек. Если после очередного обмена значение 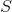уменьшилось (равномерность возросла), мы сохраняем это состояние, в противном случае продолжаем итерации до тех пор, пока не достигнем улучшения. Если проделать такие итерации некоторое большое число раз (скажем, 1000), то от диагонального расположения мы приходим к следующей картине:



Это именно то, что нам нужно — некоторое заданное количество точек, равномерно заполняющих куб заданной размерности.

Уточняющие итерации

Как только мы определились с начальной выборкой, можно приступить к построению интерполирующей поверхности для уточняющих итераций. Будем строить поверхность с помощью Radial basis functions (RBF) с кубическим базисом. Уравнение такой поверхности очень простое и компактное:



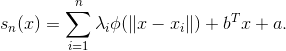
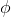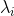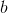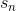Здесь — кубический базис, , , — коэффициенты, которые находятся из условия интерполяции и решения соответствующей линейной системы уравнений. Полученная поверхность построена с использованием 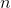точек 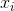и позволяет предсказать значение исходной функции в произвольной точке .

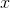После того, как начальная поверхность построена, для уточнения оптимума мы воспользуемся итерационным алгоритмом, подробно описанным здесь. Смысл алгоритма в том, чтобы найти оптимум построенной поверхности (можно даже методом Монте-Карло, поверхность намного «дешевле» исходной функции) так, чтобы новая точка находилась не ближе заданного минимального расстояния до всех остальных точек — чтобы поиск не застревал на одном месте. Это как если бы мы разместили в каждой точке ограничитель в виде мячика заданного радиуса, который бы не позволял новой точке быть слишком близко. В методе вводится функция плотности (отношение объема таких мячиков к объему куба):



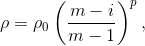
где 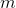— количество уточняющих итераций, 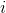— номер уточняющей итерации, 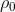— начальная плотность, а степень 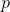определяет скорость убывания плотности с итерациями.

Выбирая те или иные значения 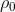и 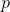, можно задавать необходимый акцент на глобальном/локальном поиске.

Пример

Для демонстрации работы метода рассмотрим задачу минимизации простой функции, например, такой:



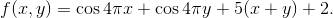
Будем искать ее минимум на области , где она выглядит вот так:



Притворимся, будто выражение функции нам неизвестно (черный ящик) и мы лишь можем вычислять ее значения в указанных точках. Запустим наш метод, используя 15 точек — 10 для LH и 5 для уточняющих итераций:



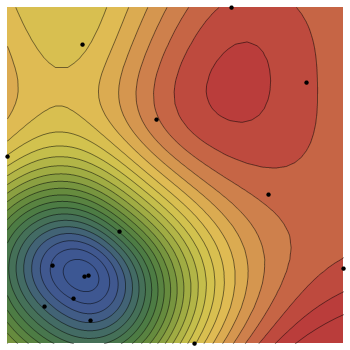
Также запустим метод, используя 30 точек — 20 для LH и 10 для уточняющих итераций:



Очевидно, что качество реконструкции исходной функции с помощью RBF-поверхности и точность метода напрямую зависят от заданного количества точек.

О глобальном оптимуме и точности метода

Если бы заданная функция обладала некоторыми свойствами (по гладкости/выпуклости/...), то наверное можно было бы построить взаимосвязь между количеством точек и точностью метода. Однако наша функция — черный ящик, а значит мы не знаем про нее абсолютно ничего. Ничто не мешает нашей функции выглядеть вот так:



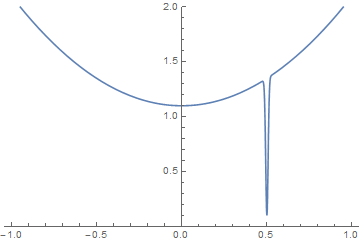
Этот искусственный пример наглядно показывает, что просто невозможно дать никаких гарантий касательно нахождения глобального оптимума (а тем более точности его нахождения).

Поэтому в метод заложена очень простая логика — пользователь вместо заданной точности указывает имеющееся вычислительное время (количество точек), а метод всего лишь эффективно использует это вычислительное время, пытаясь найти глобальный оптимум.

Ядра-ядрышки

Выше мы говорили о математических методах, позволяющих эффективно искать оптимум, экономя на вычислениях функции. Но мы забыли еще об одном — о параллельности. Почему бы не вычислять функцию в нескольких точках одновременно, используя для каждого вычисления отдельное ядро процессора? Ведь ядер сейчас немало, а реализовать такую фичу — дело несложное. Вот так выглядит велосипед на Питоне, который «мапит» заданную функцию на несколько точек в параллельном режиме:

import multiprocessing as mp

def pmap(f,batch,n):

  pool=mp.Pool(processes=n)
  res=pool.map(f,batch)
  pool.close()
  pool.join()

  return res

Эта простая штука дает прирост производительности, равный количеству используемых ядер!

Код

Код метода написан на Питоне и скорее всего не является эталоном стиля, зато простой и работает. Сделано все в виде одного модуля, включающего несколько функций.

Ссылка на GitHub

От пользователя требуется предоставить черный ящик в виде питоновской функции. Например, в случае использования внешнего пакета (через системный вызов) она может выглядеть так:

def fun(par):

  # modifying text file that contains design/model parameters
  ...
  # performing simulation in external package
  os.system(...)
  # reading results, calculating output
  ...

  return output

Аргументом функции должен быть вектор параметров, а результатом — неотрицательная скалярная величина. Запуск метода (для минимизации функции) выглядит вот так:

from blackbox import *


def fun(par):
  ...
  return output


if __name__ == '__main__':

  search(

    f=fun, # given function

    resfile='output.csv', # .csv file where iterations will be saved

    box=np.array([[-1.,1.],[-1.,1.]]), # range of values for each variable

    cores=4, # number of cores to be used

    n=8, # number of function calls on initial stage (global search)
    it=8 # number of function calls on subsequent stage (local search)

    )

Пара уточнений о том, как сохраняются и интерпретируются результаты, приведены в описании на GitHub.

На будущее

Хотелось бы допилить две вещи:

• Пока что аргументы функции задаются на независимых интервалах и пространство поиска представляет собой куб. Если же на аргументы наложены некоторые ограничения, то пространство поиска будет иметь произвольную форму. Нужно будет придумать, как удобнее всего задавать такие ограничения в коде, и, что важнее, как равномерно размещать начальные точки в области произвольной формы.
• Неплохо было бы заменить RBF-поверхность на более мощную (например, вероятностную). Это дало бы некоторый прирост к эффективности метода.

Литература

Статья с полным описанием метода

Еще пара статей по теме:

Regis, R.G. and Shoemaker, C.A., 2005. Constrained global optimization of expensive black box functions using radial basis functions. Journal of Global optimization, 31(1), pp.153-171.

Holmstrom, K., 2008. An adaptive radial basis algorithm (ARBF) for expensive black-box global optimization. Journal of Global Optimization, 41(3), pp.447-464.