Введение
Этим постом я начну цикл «Нейронные сети для новичков». Он посвящен искусственным нейронным сетям (внезапно). Целью цикла является объяснение данной математической модели. Часто после прочтения подобных статей у меня оставалось чувство недосказанности, недопонимания — НС по-прежнему оставались «черным ящиком» — в общих чертах известно, как они устроены, известно, что делают, известны входные и выходные данные. Но тем не менее полное, всестороннее понимание отсутствует. А современные библиотеки с очень приятными и удобными абстракциями только усиливают ощущение «черного ящика». Не могу сказать, что это однозначно плохо, но и разобраться в используемых инструментах тоже никогда не поздно. Поэтому моей первичной целью является подробное объяснение устройства нейронных сетей так, чтобы абсолютно ни у кого не осталось вопросов об их устройстве; так, чтобы НС не казались волшебством. Так как это не математический трактат, я ограничусь описанием нескольких методов простым языком (но не исключая формул, конечно же), предоставляя поясняющие иллюстрации и примеры.
Цикл рассчитан на базовый ВУЗовский математический уровень читающего. Код будет написан на Python3.5 с numpy 1.11. Список остальных вспомогательных библиотек будет в конце каждого поста. Абсолютно все будет написано с нуля. В качестве подопытного выбрана база MNIST — это черно-белые, центрированные изображения рукописных цифр размером 28*28 пикселей. По-умолчанию, 60000 изображений отмечены для обучения, а 10000 для тестирования. В примерах я не буду изменять распределения по-умолчанию.
Пример изображений из MNIST:
Я не буду заострять внимание на структуре MNIST и просто выложу код, который загрузит базу и сохранит в нужном формате. Этот формат в дальнейшем будет использован в примерах:
import struct
import numpy as np
import requests
import gzip
import pickle
TRAIN_IMAGES_URL = "http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz"
TRAIN_LABELS_URL = "http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz"
TEST_IMAGES_URL = "http://yann.lecun.com/exdb/mnist/t10k-images-idx3-ubyte.gz"
TEST_LABELS_URL = "http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz"
def downloader(url: str):
response = requests.get(url, stream=True)
if response.status_code != 200:
print("Response for", url, "is", response.status_code)
exit(1)
print("Downloaded", int(response.headers.get('content-length', 0)), "bytes")
decompressed = gzip.decompress(response.raw.read())
return decompressed
def load_data(images_url: str, labels_url: str) -> (np.array, np.array):
images_decompressed = downloader(images_url)
# Big endian 4 числа типа unsigned int, каждый по 4 байта
magic, size, rows, cols = struct.unpack(">IIII", images_decompressed[:16])
if magic != 2051:
print("Wrong magic for", images_url, "Probably file corrupted")
exit(2)
image_data = np.array(np.frombuffer(images_decompressed[16:], dtype=np.dtype((np.ubyte, (rows * cols,)))) / 255,
dtype=np.float32)
labels_decompressed = downloader(labels_url)
# Big endian 2 числа типа unsigned int, каждый по 4 байта
magic, size = struct.unpack(">II", labels_decompressed[:8])
if magic != 2049:
print("Wrong magic for", labels_url, "Probably file corrupted")
exit(2)
labels = np.frombuffer(labels_decompressed[8:], dtype=np.ubyte)
return image_data, labels
with open("test_images.pkl", "w+b") as output:
pickle.dump(load_data(TEST_IMAGES_URL, TEST_LABELS_URL), output)
with open("train_images.pkl", "w+b") as output:
pickle.dump(load_data(TRAIN_IMAGES_URL, TRAIN_LABELS_URL), output)
Линейная регрессия
Линейная регрессия — метод восстановления зависимости между двумя переменными. Линейная означает, что мы предполагаем, что переменные выражаются через уравнение вида:
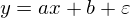Эпсилон здесь — это ошибка модели. Также для наглядности и простоты будем иметь дело с одномерной моделью — многомерность не прибавляет сложности, но иллюстрации сделать не выйдет. На секунду забудем про MNIST и сгенерируем немного данных, вытянутых в линию. Также перепишем модель (гипотезу) регрессии следующим образом: 
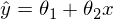. y с шапкой — это предсказанное моделью значение. 
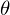1 и 2 — неизвестные параметры — основная задача эти параметры отыскать, а x — свободная переменная, ее значения нам известны. Сформулируем задачу еще раз и немного другим языком — у нас есть набор экспериментальных данных в виде пар значений 
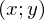и нужно найти прямую линию, на которой эти значения располагаются, найти линию, которая бы наилучшим образом обобщала экспериментальные данные. Немного кода для генерации данных:import numpy as np
import matplotlib.pyplot as plt
TOTAL = 200
STEP = 0.25
def func(x):
return 0.2 * x + 3
def generate_sample(total=TOTAL):
x = 0
while x < total * STEP:
yield func(x) + np.random.uniform(-1, 1) * np.random.uniform(2, 8)
x += STEP
X = np.arange(0, TOTAL * STEP, STEP)
Y = np.array([y for y in generate_sample(TOTAL)])
Y_real = np.array([func(x) for x in X])
plt.plot(X, Y, 'bo')
plt.plot(X, Y_real, 'g', linewidth=2.0)
plt.show()
В результате должно получиться что-то вроде этого — достаточно случайно для неподготовленного человеческого глаза:
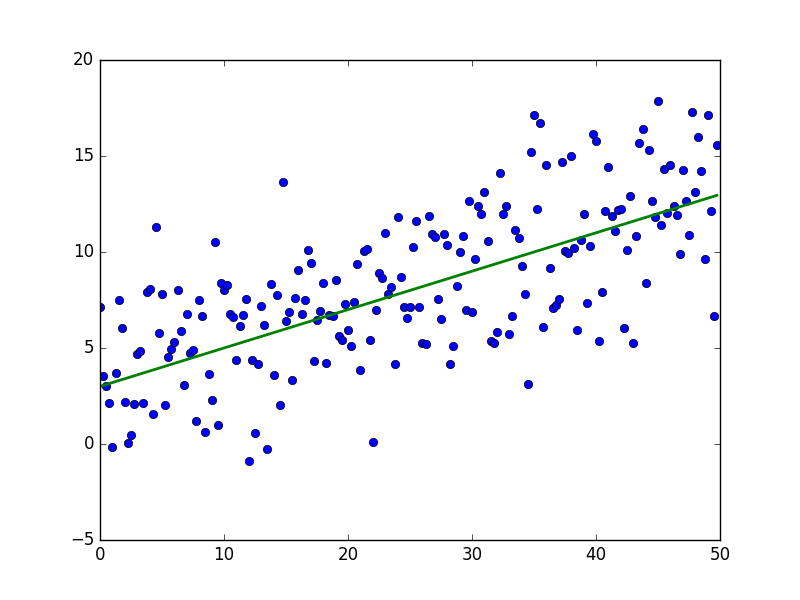
Зеленая линия — это «база» — сверху и снизу от этой линии случайным образом распределены данные, распределение равномерное. Уравнение для зеленой линии:
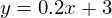
Метод наименьших квадратов
Суть МНК заключается в том, чтобы отыскать такие параметры
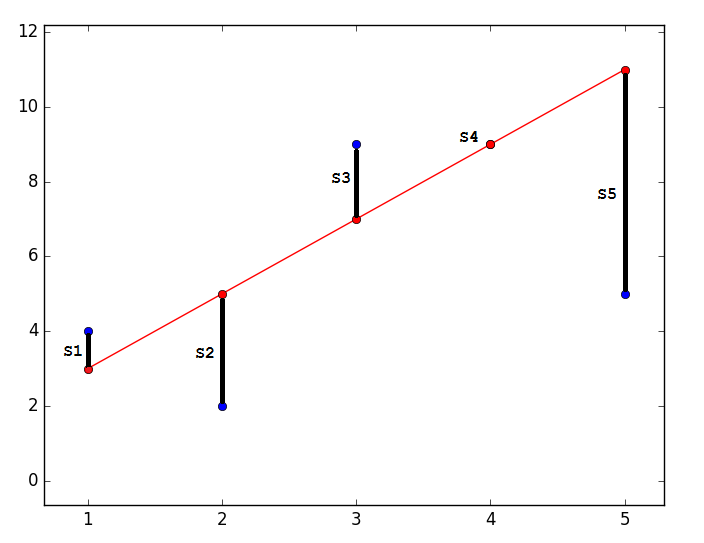
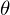, чтобы предсказанное значение было наиболее близким к реальному. Графически это выражается как-то так:import matplotlib.pyplot as plt
plt.plot([1, 2, 3, 4, 5], [4, 2, 9, 9, 5], 'bo')
plt.plot([1, 2, 3, 4, 5], [3, 5, 7, 9, 11], '-ro')
plt.show()
Наиболее близким — значит, что вектор
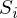должен иметь наименьшую возможную длину. Так как вектор не единственный, то постулируется, что сумма квадратов длин всех векторов должна стремится к минимуму, учитывая вектор параметров 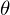. На мой взгляд, довольно логичный метод, умозрительный. Тем не менее, существует математическое доказательство корректности этого метода Ремарка: под длиной будем понимать Евклидову метрику, хотя это необязательно. Ремарка 2: обратите внимание, что сумма квадратов. Опять-таки, никто не запретит попробовать минимизировать просто сумму длин. На этой картинке красные точки — предсказанное значение (
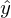), синие — полученные в результате эксперимента(y без шапки). 
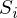— это как раз различие между ними, длина вектора.Математически это выглядит так:
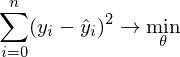— требуется найти такой вектор 
, при котором выражение 
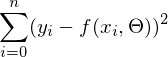достигает минимума. Функция f в этом выражении — это: 
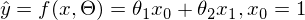или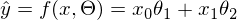 
Я долго думал, стоит ли сразу переходить к векторизации кода и в итоге без нее статья слишком удлиняется. Поэтому введем новые обозначения:
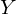— вектор, состоящий из значений зависимой переменной y —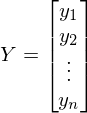 
— вектор параметров — 
A — матрица из значений свободной переменной x. В данном случае первый столбец равен 1 (отсутствует x_0) —
. В одномерном случае в матрице A только два столбца —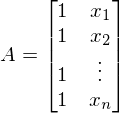 
После новых обозначений уравнение линии переходит в матричное уравнение следующего вида:
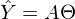. В этом уравнении 2 неизвестных — предсказанные значения и параметры. Мы можем попробовать узнать параметры из такого же уравнения, но с известными значениями: 
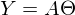Иначе можно представить как систему уравнений: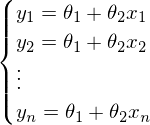 
Казалось бы, что все известно — и вектор Y, и вектор X — остается только решить уравнение. Большая проблема заключается в том, что система может не иметь решений — иначе, у матрицы A может не существовать обратной матрицы. Простой пример системы без решения — любые три\четыре\n точки не на одной прямой\плоскости\гиперплоскости — это приводит к тому, что матрица А становится неквадратной, а значит по определению нет обратной матрицы
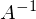.Наглядный пример невозможности решения «простым способ» (каким-нибудь методом Гаусса решить систему):
Система выглядит так:
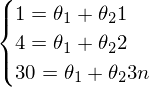— вряд ли выйдет отыскать решения для такой системы. Как итог невозможно построить линию через эти три точки — можно лишь построить примерно верное решение.
Такое отступление — это объяснение того, зачем вообще понадобился МНК и его братья. Минимизации функции стоимости (функции потерь) и невозможность (ненужность, вредность) найти абсолютно точное решение — одни из самых базовых идей, что лежат в основе нейронных сетей. Но до них еще далеко, а пока вернемся к методу наименьших квадратов.
МНК говорит нам, что необходимо найти минимум суммы квадратов векторов вида:
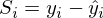Сумму квадратов с учетом того, что все преобразовано в вектора\матрицы можно записать следующим образом: 
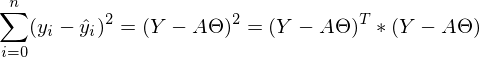.У меня не повернется язык назвать это тривиальным преобразованием, новичкам бывает довольно сложно уйти от простых переменных к векторам поэтому я распишу все это выражение полностью в «раскрытых» векторах. Опять-таки, чтобы ни одна строка не была непонятым «волшебством».
Для начала просто «раскроем» вектора в соответствии с их определением:
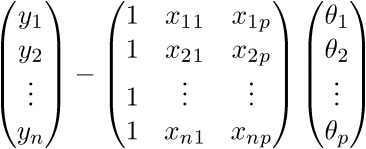.Проверим размерность — для матрицы А она равна (n;p), а для вектора
— (p;1), а для вектора 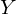— (n;1). В результате получим разницу двух векторов размерностью (n;1) —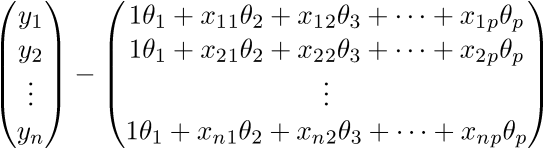 
Сверимся с определением — по определению выходит, что каждая строка правой матрицы равна
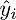. Запишем далее: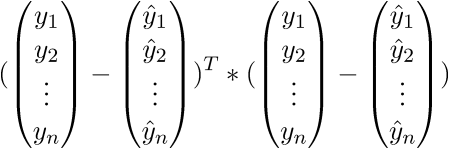 
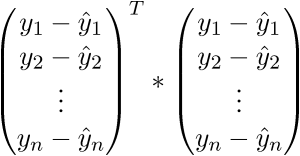
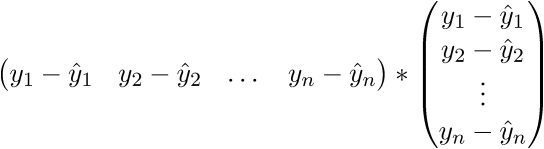
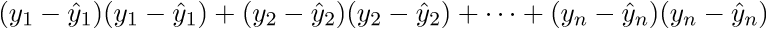
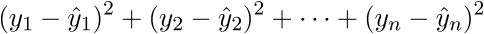
В итоге последняя строка и есть сумма квадратов длин, как нам и нужно. Каждый раз, конечно же, такие фокусы в уме проворачивать довольно долго, но к векторной нотации можно привыкнуть быстро. У этого есть и плюс для программиста — удобней работать и портировать код для GPU, где ехал вектор через вектор. Я как-то портировал генерацию шума Перлина на GPU и примерное понимание векторной нотации неплохо облегчило работу. Есть и минус — придется постоянно лезть в интернет, чтобы вспомнить тождества и правила линейной алгебры. После доказательства верности векторной нотации перейдем к дальнейшим преобразованиям:
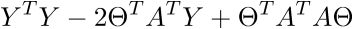
Здесь использованы свойства транспонирования матриц — а именно транспонирование суммы и произведения. А также тот факт, что выражения
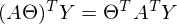и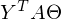 
есть константа. Доказать можно взяв размерность матриц из их определения и посчитав размерность выражения после всех умножений: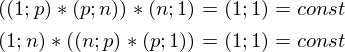 
Константу можно представить как симметричную матрицу, следовательно:
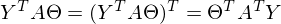
После преобразований и раскрытия скобок, приходит время решить-таки поставленную задачу — найти минимум данного выражения, учитывая
. Минимум находится весьма буднично — приравнивая первый дифференциал по к нулю. По-хорошему, нужно сначала доказать, что этот минимум вообще существует, предлагаю доказательство опустить и подсмотреть его в литературе самостоятельно. Интуитивно и так понятно, что функция квадратичная — парабола, и минимум у нее есть.Итак,
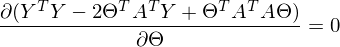
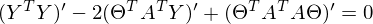
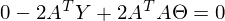
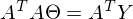
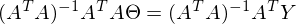
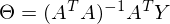
Часть
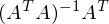называют псевдообратной матрицей.Теперь в наличии все нужные формулы. Последовательность действий такая:
1) Сгенерировать набор экспериментальных данных.
2) Создать матрицу A.
3) Найти псевдообратную матрицу
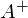.4) Найти
После этого задача будет решена — у нас в распоряжении будут параметры прямой линии, наилучшим образом обобщающей экспериментальные данные. Иначе, у нас окажутся параметры для прямой, наилучшим образом выражающей линейную зависимость одной переменной от другой — именно это и требовалось.
import numpy as np
import matplotlib.pyplot as plt
TOTAL = 200
STEP = 0.25
def func(x):
return 0.2 * x + 3
def prediction(theta):
return theta[0] + theta[1] * x
def generate_sample(total=TOTAL):
x = 0
while x < total * STEP:
yield func(x) + np.random.uniform(-1, 1) * np.random.uniform(2, 8)
x += STEP
X = np.arange(0, TOTAL * STEP, STEP)
Y = np.array([y for y in generate_sample(TOTAL)])
Y_real = np.array([func(x) for x in X])
A = np.empty((TOTAL, 2))
A[:, 0] = 1
A[:, 1] = X
theta = np.linalg.pinv(A).dot(Y)
print(theta)
Y_prediction = A.dot(theta)
error = np.abs(Y_real - Y_prediction)
print("Error sum:", sum(error))
plt.plot(X, Y, 'bo')
plt.plot(X, Y_real, 'g', linewidth=2.0)
plt.plot(X, Y_prediction, 'r', linewidth=2.0)
plt.show()
И результаты:
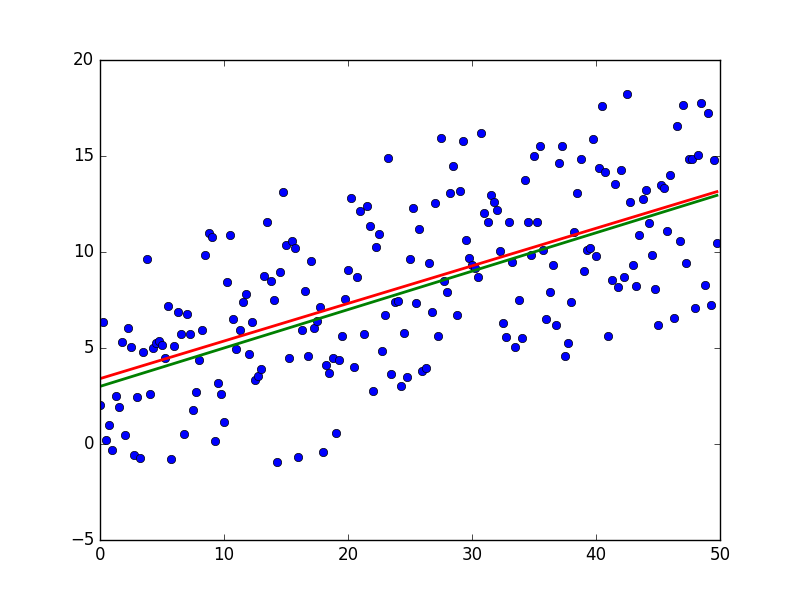
Красная линия была предсказана и почти совпадает с зеленой «базой». Параметры в моем запуске равны: [3.40470411, 0.19575733]. Попробовать предсказать значения не выйдет, потому что пока неизвестно распределение ошибок модели. Все, что можно сделать, так это проверить, правда ли для данного случая МНК будет подходящим и лучшим методом для обобщения. Условий три:
1) Мат ожидание ошибок равно нулю.
2) Дисперсия ошибок — постоянная величина.
3) Отсутствует корреляция ошибок в разных измерениях. Ковариация равна нулю.
Для этого я дополнил пример вычислением необходимых величин и провел измерения дважды:
import numpy as np
import matplotlib.pyplot as plt
TOTAL = 200
STEP = 0.25
def func(x):
return 0.2 * x + 3
def prediction(theta):
return theta[0] + theta[1] * x
def generate_sample(total=TOTAL):
x = 0
while x < total * STEP:
yield func(x) + np.random.uniform(-1, 1) * np.random.uniform(2, 8)
x += STEP
X = np.arange(0, TOTAL * STEP, STEP)
Y = np.array([y for y in generate_sample(TOTAL)])
Y_real = np.array([func(x) for x in X])
A = np.empty((TOTAL, 2))
A[:, 0] = 1
A[:, 1] = X
theta = np.linalg.pinv(A).dot(Y)
print(theta)
Y_prediction = A.dot(theta)
error = Y - Y_prediction
error_squared = error ** 2
M = sum(error) / len(error)
M_squared = M ** 2
D = sum([sq - M_squared for sq in error_squared]) / len(error)
print("M:", M)
print("D:", D)
plt.plot(X, Y, 'bo')
plt.plot(X, Y_real, 'g', linewidth=2.0)
plt.plot(X, Y_prediction, 'r', linewidth=2.0)
plt.show()
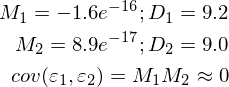
Неидеально, но все без обмана работает так, как и ожидалось.
Следующая часть.
Полный список библиотек для запуска примеров: numpy, matplotlib, requests.
Материалы, использованные в статье — https://github.com/m9psy/neural_nework_habr_guide
Комментарии (42)
Fontanka135
03.08.2016 13:47+6Причём тут название статьи "искусственные нейронные сети для новичков" и рассказ про МНК и линейную регрессию? Конечно, понимаю, что это "часть 1", но заголовок вводит в заблуждение.
BelBES
03.08.2016 14:01Пусть у нас есть однослойная нейронная сеть с функцией активации вида Identity. Тогда такую сеть можно записать в виде w * x + b = y, где w, b — обучаемые параметры. Чем это не линейная регрессия?
akhmelev
03.08.2016 14:51+2Действительно плохое название. Лучше что-то типа «что было до...»
BelBES
03.08.2016 15:02Ну это «за уши» притянуто. Просто после приведения подобных и т. д. все будет выражено через один нейрон с линейной функцией активации. Сети с линейными нейронами сколь угодной глубины и сложности вырождаются именно в это. Приводить надо обязательно, дабы оптимизировать емкость вычислений. А один нейрон — это не сеть.
Я лишь хочу сказать, что формально это нейронная сеть. Также, как и, например, SVM — частный случай нейронных сетей. Тот же Хайкин в своем "Нейронные Сети. Полный Курс" также использует термин нейронная сеть применительно к таким моделям.
m9_psy
03.08.2016 15:13+3Все эти модели приведут в конечном итоге к нейронным сетям в их обычном понимании — со слоями, нейронами и т.д. Первые части всего лишь введение и в следующих частях они плавно перетекут в ИНС. Я хотел начать абсолютно с самого-самого начала, а не рвать с места в карьер, начиная со слоев и синапсов. Даже если умозрительно концепция понятна, модель НС совсем не самая тривиальная. Начав с азов, я закончу какими-нибудь сверточными сетями или изобрету какую-нибудь новую схему и хочу, чтобы объяснение было понятно максимальному числу читателей. А заголовок как раз явно обозначает, что описанные модели используются в НС или похожи на них (например, линейная во многом похожа на логистическую и так далее). Такой длинный путь к НС выдуман не мной — как пример подойдет CS229. А еще многие модели удобней модифицировать, взяв «чистую» реализацию, а не в составе НС. Например, модифицированный градиентный спуск, о котором будет следующая часть, намного легче воспринять отдельно в контексте линейной регрессии, чем в многослойной ИНС.
knagaev
04.08.2016 15:30Что-то мне кажется, что НС всё-таки ближе линейный классификатор, а не регрессия.
Так что от печки лучше было бы идти от линейных классификаторов.
Dark_Daiver
04.08.2016 16:11А почему? Вроде НС вполне можно использовать для регрессии.
А для обучения (в смысле обучения людей) линейный классификатор чуть хуже, т.к. чуть больше формул и чуть менее наглядные примерыknagaev
04.08.2016 16:27Потому что модель нейрона при подаче сигналов возбуждения на его входы по линейной функции активации (сумма взвешенных сигналов на входе) выдаёт или не выдаёт сигнал на выходе.
А это и есть простейший линейный классификатор.Dark_Daiver
04.08.2016 16:34А кто нам мешает использовать модель нейрона, который возвращает пришедший сигнал как он есть? Получим вполне себе линейный регрессор.
Для новичков линейная модель будет явно проще. А потом сверху можно и пороговую ф-ию накрутить, или чего-нить еще.knagaev
04.08.2016 17:08Ничего не мешает.
Но если идти от печки, то нужно смотреть в сторону перцептрона
Там написано явно «Так же как и A-элементы, R-элемент подсчитывает сумму значений входных сигналов, помноженных на веса (линейную форму). R-элемент, а вместе с ним и элементарный перцептрон, выдаёт «1», если линейная форма превышает порог ?, иначе на выходе будет «?1».»
А это и есть чистой воды классификатор.
AlexAntonov
03.08.2016 13:53Интересная статься. Только надо наверно более явно обозначить, что цикл про НН, а конкретно данная статья всё-таки про линейную регрессию.
hose314
03.08.2016 13:54+1Давате все-таки не называть вещи своими именами, это ведь математика, тут так нельзя.
Линейная означает, что мы предполагаем, что переменные выражаются через уравнение вида...
linear regression definition
Roman_Kh
03.08.2016 14:36+3Для начала просто «раскроем» вектора в соответствии с их определением
После этих слов нарисованы неправильные матрицы:
- матрица Х имеет размерность N на (p+1)
- а матрица ? имеет размерность p на 1
Их не получится перемножить. Вы забыли ?0.
BansheeRotary
03.08.2016 16:20Насчет
Опять-таки, никто не запретит попробовать минимизировать просто сумму длин.
А разве метод наименьших модулей вообще можно использовать на практике? Там не получится трюк с приравниванием первой производной нулю.Dark_Daiver
03.08.2016 16:43Насколько я помню, там используются немного другие трюки, вроде Soft thresholding https://en.wikipedia.org/wiki/Proximal_gradient_methods_for_learning
Dark_Daiver
03.08.2016 16:46Еще можно притвориться что оптимизируешь сумму модулей при помощи взвешивания и МНК (IRLS) https://en.wikipedia.org/wiki/Iteratively_reweighted_least_squares
Еще (могу ошибиться, на самом деле) вроде стохастический градиентный спуск нормально работает с негладкими ф-иями потерь.
m9_psy
03.08.2016 16:59Можно, конечно. И метод этот, естественно, статистически корректен, при определенных допущениях в распределении ошибок. А минимум находят численными методами.
Gokjer
03.08.2016 18:26+6Статья выглядит примерно так:
А сейчас, друзья, я расскажу вам про нейронные сети. Будем использовать такие-то картинки.
Откуда взялись эти понятия? Зачем они нужны? Куда успели исчезнуть нейросети? Причем еще до своего появления.
<вакуум>
Линейная регрессия — это…
Метод наименьших квадратов — это..
Вообще тема интересная и про методы неплохо написано, но коли уж это гайд, то неплохо было бы мотивировать возникновение данных понятий. Иначе у читателей никуда не денетсячувство недосказанности, недопонимания.
m9_psy
03.08.2016 18:40Линейная регрессия — это подвид обобщенной линейной модели с указанием, что ошибки распределены по нормальному закону. Начинать статью для новичков с GLM? Это уже будут далеко не новички. Новичкам (особенно со слабой математической базой) требуются простые, интуитивные примеры, море картинок, анимаций, идеализированные одномерные примеры. Я как-то встречал объяснение градиентного спуска будто бы это альпинист с горы шагает. Тогда меня это покоробило, теперь же я думаю, что любые методы хороши, если работают. А до GLM и максимального правдоподобия я также доберусь, но не стоит спешить. И слова «нейронные сети» еще не будет 3 или 4 части. Зато подойдя к этой модели вплотную, читающий будет во всеоружии.
Gokjer
04.08.2016 12:28+1Начинать статью для новичков с GLM?
Нет, но стоит объяснить читателю, зачем вы даете этот материал и как он вообще связан с нейросетями. Поймите, даже в книжках по чистой математике обычно дается мотивировка перед вводом нового понятия. А у вас не книжка по математике, а хабр, где по умолчанию собрались люди с более прикладным подходом. Если слов «нейронные сети» не будет еще 3-4 части, то c таким обилием формул вы рискуете растерять больше 90% читателей.
Ну и в конце концов, называйте тогда статью не «ИНС для новичков», а «Математическая теория, необходимая для ИНС»(theoretical prerequisites).
Roman_Kh
04.08.2016 13:12-1Линейная регрессия — это подвид обобщенной линейной модели с указанием, что ошибки распределены по нормальному закону
И опять неверно. Линейная регрессии не требует нормальности ошибок.
perfect_genius
03.08.2016 18:43+1"… для новичков, которые могут смотреть спокойно на формулы"
m9_psy
03.08.2016 19:05От них никуда не денешься. ИНС, в конце концов, математическая теория, как бы ее не натягивали на гипотетические модели мозга и нейронов. Я попытался объяснить все преобразования и раскрыть все, что обычно опускается в литературе, но мог и упустить что-нибудь. Что конкретно неясно и где сломалось «понимание»?
perfect_genius
03.08.2016 21:09Не стоит отвлекаться на мой комментарий. Просто знайте, что для многих людей формулы — это как инопланетные иероглифы.
m9_psy
03.08.2016 21:15На самом деле стоит — я ведь не для профессоров или роботов пишу. Правда, некая база все же должна быть — я ее обозначил как базовый вузовский уровень, держа в уме технические вузы — линейная алгебра, мат. анализ, теория вероятности.
yorko
04.08.2016 02:27+2Для новичков то как раз это очень нагруженная подача материала.
МНК можно объяснить и без дифференцирования таких сложных матричных выражений. Да и косяки с индексами…
Но интересно посмотреть, что дальше будет.
Не планируете материал сделать в виде тетрадок Jupyter?IIvana
04.08.2016 05:56+1Соглашусь с комментарием. Если бы я не знал хорошо МНК, не выводил его формулы сам, не объяснял вывод сыну — ничего бы не понял из нагромождения формул и непонятного описания. Все это можно подать на порядок проще и понятнее. Если дальше про те вещи, которые я не знаю, будет в таком же духе — боюсь, понять это будет тяжело. Причем, самое обидное — не по причине собственной сложности моделей и концепций.
m9_psy
04.08.2016 09:30-1Если у вас есть ссылки на более доступное объяснение, я был бы признателен, если вы их предоставите. Перед публикацией следующей части я вместе с правкой опечаток добавил бы больше информации. Jupyter не планирую. На Хабр нельзя будет вставить тетрадь, а форматирование съедает достаточно времени.
Mugik
04.08.2016 09:45Если честно — каша полная. И это еще на относительно простых методах. Что будет происходить, когда дело дойдет до EM алгоритмов страшно подумать.
Так уж у нас повелось, что в Российской литературе любят кашу и в университетах старые преподаватели тоже любят. Не задумывались опубликовать это? Там бы это смотрелось лучше. Что касается новичков и статьи на хабре — вопрос, но скорее нет, чем да.
ternaus
09.08.2016 00:53Для тех, кто понимает по английски сильно рекомендую курс лекций: https://www.youtube.com/watch?v=PlhFWT7vAEw
От азов линейной регрессии до особо хитрых архитектур, причем четко и структурировано.
BelBES
Пока собирался сесть за напсиание практического курса по Deep Learning, кто-то уже сел и начал писать)
Dark_Daiver
А вы все равно пишите) ИМХО, хабру не хватает продвинутых статей по ML/DL
centrin0
Пишите. Есть большая вероятность что второй части не будет — автор уже получил инвайт.
m9_psy
Без паники, все будет. И инвайт не имеет столь большой ценности, чтобы исключительно ради него обещать обещать продолжение.
shebeko
Ещё бы практическое руководство по готовым (желательно бесплатным) инструментам.
Типа какчаем такую тулзу, запускаем такой батник, вот так скармливаем картинки — опа, получили автоматический распознаватель сисек
KvanTTT
Поддерживаю. А еще хотелось бы больше узнать о применении нейросетей в различных областях (звук, текст) и о комбинации с другими алгоритмами (AlphaGo), а не только в обработке изображений. Все-таки картинки — довольно заезженная тема уже.