На рисунке изображены схема из 8 возможных триграмм, взятая из книги [1]

Естественные языки могут быть охарактеризованы распределением частот встречаемости своих элементов, таких как слова, отдельные буквы или последовательности букв (N-граммы). Формально N-граммой называется строка из N символов, принадлежащих некоторому алфавиту, состоящему из конечного числа символов. О теоретических и прикладных вопросах применения аппарата N-грамм для автоматической коррекции текста можно прочесть в работе [2].

В данной статье мы будем рассматривать только алфавит, состоящий из букв русского языка, далее мы расскажем о возможностях применения триграмм (последовательностей из трех символов) для постобработки (коррекции с целью уменьшения ошибок) результатов распознавания русскоязычных документов. В качестве механизма распознавания выступали сверточные нейронные сети.

1. Описание модели триграммы

Модель триграмм состоит из набора (словаря) троек символов {g_i1, g_i2, g_i3} и приписанного им веса w_i. Триграммы упорядочены по весу, больший вес означает большую частоту встречаемости триграммы в естественном языке, точнее в некотором корпусе текстов на естественном языке.

В идеальном случае под весом  триграммы мы понимаем вероятность её встречаемости в естественном языке. Разумеется, на различных выборках текстов естественного языка мы можем получать различающиеся веса триграмм. В качестве примера можно рассмотреть тексты классической литературы и таблицы, содержащие аббревиатуры изделий, очевидно, что для этих случаев встречаемость  триграмм будет сильно разниться. В то же самое время извлечение триграмм из корпуса однородных слов, позволяет получить стабильные оценки весов триграмм.

Мы расскажем об извлечении триграмм из больших наборов фамилий, имен и отчеств граждан Российской Федерации и об использовании найденных триграмм для коррекции результатов распознавания полей «Фамилия», «Имя» и «Отчество» в паспорте гражданина Российской Федерации. Ранее мы рассказывали о своих программных решениях для распознавания паспорта [3, 4], в которых могут быть применены результаты данной статьи.

В нашем распоряжении имелись три корпуса слов: словари фамилий, имен и отчеств граждан Российской Федерации. Из каждого из корпусов были извлечены триграммы. Для каждого слова {c₁,c₂,…,c_n} в котором c_i–символ русского языка (прописные и строчные буквы не различались) в начало и конец слова добавлялись два фиктивных символаc_F:  {c_F, c_F, c₁, c₂, …, c_n,
c_F, c_F}. Это было сделано для того, чтобы каждому из символов c_i можно было сопоставить триграммы <c_i-2, c_i-1, c_i> и <c_i, c_i+1, c_i+2>, например, c₁ можно сопоставить триграмму <c_F, c_F, c₁>. Далее будем рассматривать слова с добавленными в алфавит символами c_F. Для каждой тройки символов <g₁, g₂, g₃>мы подсчитали количество экземпляров этой тройки во всех словах корпуса, отнормировали его на число возможных триграмм и взяли нормированное значение в качестве веса (сумма  нормированных весов ?(g₁, g₂, g₃), равна единице).

Использованный большой корпус фамилий (более 1 500 000 фамилий в случайном порядке, из – них различных около 183 000 различных фамилий), собранных ранее нами из открытых источников, позволил построить словарь триграмм с весами, которые мало зависят от размера выборки слов. Для примера рассмотрим часто встречающие в фамилиях триграммы

{О, В, А}, {К, О, В}, {Н, О, В}, {И, Н, А}, {Е, В, А},

веса которых мы вычислим на выборках различного объема, все выборки извлекаются из корпуса фамилий. На рисунке 1 представлены графики зависимости весов этих триграмм в зависимости от объема выборки, которые характеризуют стабильность определения весов указанных триграмм при объеме выборки, превышающий 50 000 слов.

Обратим внимание на то, что самой распространенной триграммой для корпуса фамилий являются {А, c_F,
c_F} и {В, А, c_F} c весами 0.044 и 0.033, соответственно.

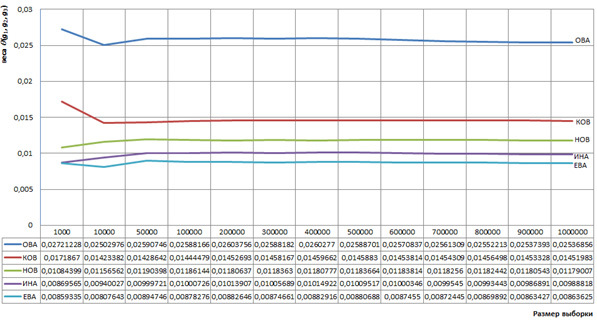
Рисунок 1. Графики примеров зависимости весов триграмм в зависимости от объема выборки

Аналогично были построены словари триграмм для имен и отчеств, в них при использования выборок слов большого объема веса часто встречающихся триграмм также вычисляются стабильно.

2. Описание результатов распознавания

Результаты распознавания символа представлены альтернативами (c_j, p_j):  

(c₁, p₁), (c₂, p₂), …, (c_n, p_q),

где c_j – код символа, а p_j– оценка надежности распознавания символа (далее – оценки распознавания). Если p_j=1, то символ c_j распознан с наибольшей надежностью, а если p_j=0, то – с наименьшей. При этом c_j принадлежит алфавиту распознавания, состоящего из q символов. Все оценки распознавания обладают нормировкой:

0? p_j ?1

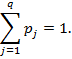
Тогда результаты распознавания слова, состоящего из n символов (знакомест) выглядят следующим образом:

(c¹₁, p¹₁), (c¹₂, p¹₂), …, (c¹_n, p¹_n)

(c²₁, p²₁), (c²₂, p²₂), …, (c²_n, p²_n)

…

(c^q₁, p^q₁), (c^q₂, p^q₂), …, (c^q_n, p^q_n).

Механизм распознавания символа может ошибаться. Распознанное слово считается распознанным с ошибками или без ошибок в зависимости от различия или совпадения  известного «идеального» слова c^*₁c^*₂ … c^*_n, которое заранее было задано человеком, с  последовательностью символов c¹₁c¹₂ … c¹_n, извлеченных из первых альтернатив {(c¹₁, p¹₁), (c¹₂, p¹₂), … (c¹_n, p¹_n)}. Определим для набора распознанных слов точность распознавания как долю слов, распознанных без ошибок.

Ниже приведен пример результатов распознавания фамилии «ЕПИФАНОВ»:

В примере одно знакоместо (буква «Н») распознано с ошибкой, поэтому все слово будет считаться как распознанное ошибочно.

Для описанных далее экспериментов были использованы два тестовых набора данных: Т₁ (2 722 слов, состоящих из 22 103 символов с низким качеством оцифровки и, соответственно с невысокой точностью распознавания) и Т₂ (2354 слов, состоящих из 19230 символов со средним качеством оцифровки и более надежным распознаванием). Набор Т₁ состоял из 896 примеров фамилий, 915 примеров имен, 911 примеров отчеств, а набор Т₂ – из 776 примеров фамилий, 794 примеров имен и 784 примеров отчеств соответственно.

Выше было написано, что оценки распознавания p^k_j интерпретировались как вероятности. Посмотрим на наборах Т₁ и Т₂, как коррелируют оценки распознавания p^k_j с количеством случившихся ошибок. Для этого построим гистограмму количества ошибок нашего механизма распознавания, случившихся с символами с оценками p^k_j из определенного диапазона отрезка [0,1]. Для наглядности разобьем отрезок [0,1] на 32 интервала [0, 1/32), [1/32, 2/32), … [31/32, 1] и для множества распознанных символов с оценками p^k_j из интервала [d/32, (d+1)/32) подсчитаем количество ошибочно распознанных символов. Эта гистограммы приведена на рисунке 2, вид гистограммы свидетельствует в пользу интерпретации оценок распознавания p^k_j как вероятностей, поскольку при малых значениях оценок наблюдается много ошибок, а при больших значениях (близких к 1) — мало. Точнее, при больших значениях оценок распознавания (более 26/32) ошибки вообще отсутствуют. Мы не стали делать более точных исследований корреляции оценок распознавания и вероятностей (частот) появления ошибок по причине ограниченного объема наборов Т₁ и Т₂.

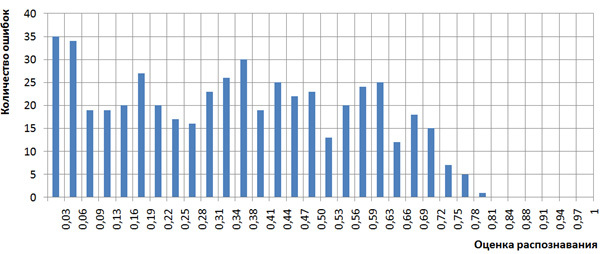
Рисунок 2. Гистограмма количества ошибок распознавания в зависимости от оценок распознавания

3. Алгоритмы коррекции результатов распознавания с помощью триграмм

Опишем простой алгоритм 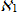для коррекции результатов распознавания.

Для всех символов с^k_i для 1?i?n, 1?k?q (т.е. для всех символов, не являющихся фиктивными) рассмотрим два предшествующих ему символа с^k_i-2, с^k_i-1, которые считаются уже выбранными (зафиксированными) и используя готовые триграммы <с^k_i-2, с^k_i-1, с^k_i>, содержащие символ с^k_i, вычислим новую оценку:

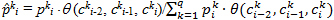
отсортируем альтернативы по новым значениям 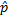^k_iи зафиксируем символ для коррекции следующего символа с^k_i+1. То есть вначале пересчитаем значения оценок для первого символа слова с учетом двух фиктивных символов, которые мы считаем выбранными, и зафиксируем первый символ. После пересчета оценок очередного символа перейдем к следующему за ним символу и так далее.

В формулах использовались предположения о том, что ? (с^k_i-2, с^k_i-1,с^k_i) и p^k_i являются вероятностями. Мы ожидали от алгоритма 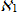исправления некоторых ошибок распознавания за счет того, что неверные и редко встречающиеся тройки распознанных символов с^k_i-2, с^k_i-1, с^k_i будут заменены на встречающиеся более часто.

Рассмотрим результаты работы алгоритма 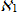на наборах Т₁ и Т₂, сведенные в таблицы 1 и 2. В этих и последующих аналогичных таблицах содержатся данные о словах, которые были распознаны с ошибками, и о безошибочно распознанных словах и используются следующие характеристики:

n₁ – количество слов без ошибок и в исходном распознавании и  при использовании механизма триграмм;

n₂ – количество слов с ошибками в исходном распознавании, не исправленные триграммами;

n₃ – количество слов с ошибками в исходном распознавании, исправленные триграммами

n₄ – количество слов без ошибок в исходном распознавании, в которые применение триграмм привнесло ошибки.

Таблица 1. Результаты работы алгоритма 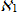на тестовом наборе Т₁

	Фамилия	Имя	Отчество
n1	811 (90.51%)	840 (91.80%)	827 (90.78%)
n2	44 (4.91%)	28 (3.06%)	31 (3.40%)
n3	36 (4.02%)	38 (4.15%)	48 (5.27%)
n4	5 (0.56%)	9 (0.98%)	5 (0.55%)

Таблица 2. Результаты работы алгоритма 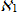на тестовом наборе Т₂

	Фамилия	Имя	Отчество
n1	736 (94.85%)	760 (95.72%)	747 (95.28%)
n2	16 (2.06%)	7 (0.88%)	9 (1.15%)
n3	21 (2.71%)	24 (3.02%)	26 (3.32%)
n4	3 (0.39%)	3 (0.38%)	2 (0.26%)

Из таблиц следует, что алгоритм корректировки 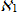дает интересные результаты, поскольку триграммами исправляется больше ошибок, чем привносится. В то же самое время возникает вопрос, как можно объяснить зависимость символа слова от двух предыдущих символов? Этот вопрос остается без ответа, такая зависимость не может быть обоснована. Однако принятая зависимость способствовала созданию очень простого алгоритма.

Не будем подвергать описанный алгоритм 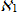дальнейшей критике, отметим только, что можно придумать множество аналогичных простых алгоритмов, например, с зависимостью символа от двух последующих или от двух соседних символов, и эти алгоритмы также дадут приемлемые результаты.

Мы поставили целью разработать алгоритм без привлечения условий зависимости символов от соседних символов, предполагая, что такой алгоритм, будучи более строгим, работал бы лучше, чем 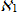. Разработанный алгоритм корректировки результатов распознавания с помощью триграмм основан на вычислениях маргинальных распределений и байесовских сетей.

Для слова из n символов с каждым знакоместом ассоциируем случайную величину 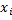со значениями в конечном пространстве состояний 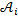и положим, что 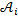является алфавитом распознавания A, то есть множеством букв русского языка, в котором не различаются прописные и строчные буквы. Обозначим через N = {1,…,n} множество индексов. Назовем произведение 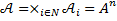пространством конечных конфигураций вектора 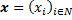. Далее построим граф 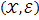по следующему правилу. Множество является множеством вершин графа. Будем считать, что с каждой тройкой вершин <x_j,x_j+1,x_j+2> ассоциирована нормированная функция весов триграмм 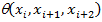. Соединим ребрами вершины из тройки между собой, совокупность полученных ребер образует множество .

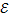Выпишем формулу для совместного распределения вероятностей

/

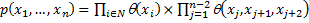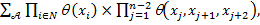
где 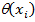– функция оценок распознавания для i-го знакоместа, 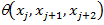– нормированная функция весов триграмм.

Для пересчета оценок достаточно посчитать маргинальные распределения

.

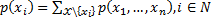Вычисление маргинальных распределений мы реализовали с помощью алгоритма HUGIN [5, 6]. Не раскрывая подробностей реализации, укажем, что этот алгоритм является существенно более сложным, чем алгоритм .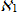

Результаты работы алгоритма на тех же самых наборах Т₁ и Т₂ сведены в таблицы 3 и 4, при этом в таблицы добавлены результаты работы алгоритма 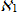для сравнения. Также в таблицы 3 и 4 добавлены характеристики точности алгоритмов.

Таблица 3. Результаты работы алгоритмов 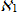и на тестовом наборе Т₁

	Фамилия		Имя		Отчество
	алгоритм	алгоритм	алгоритм	алгоритм	алгоритм	алгоритм
n1	811 (90.51%)	815 (90.96%)	840 (91.80%)	845 (92.35%)	827 (90.78%)	831 (91.22%)
n2	44 (4.91%)	38 (4.24%)	28 (3.06%)	30 (3.28%)	31 (3.40%)	21 (2.31%)
n3	36 (4.02%)	42 (4.69%)	38 (4.15%)	36 (3.93%)	48 (5.27%)	58 (6.37%)
n4	5 (0.56%)	1 (0.11%)	9 (0.98%)	4 (0.44%)	5 (0.55%)	1 (0.11%)
Точность исходного распознавания	91.07%		92.79%		91.33%
Точность с триграммами	94.53%	95.65%	95.96%	96.28%	96.05%)	97.59%
Выигрыш в точности при использовании триграмм	3.46%	4.58%	3.17%	3.50%	4.72%	6.26%

Таблица 4. Результаты работы алгоритмов 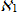и на тестовом наборе Т₂

	Фамилия		Имя		Отчество
	алгоритм	алгоритм	алгоритм	алгоритм	алгоритм	алгоритм
n1	736 (94.85%)	737 (94.97%)	760 (95.72%)	762 (95.97%)	747 (95.28%)	749 (95.54%)
n2	16 (2.06%)	12 (1.55%)	7 (0.88%)	5 (0.63%)	9 (1.15%)	8 (1.02%)
n3	21 (2.71%)	25 (3.22%)	24 (3.02%)	26 (3.27%)	26 (3.32%)	27 (3.44%)
n4	3 (0.39%)	2 (0.26%)	3 (0.38%)	1 (0.13%)	2 (0.26%)	0 (0.0%)
Точность исходного распознавания	95.23%		96.10%		95.54%
Точность с триграммами	97.55%	98.20%	98.74%)	788 (99.24%)	773 (98.60%)	776 (98.98%)
Выигрыш в точности при использовании триграмм	2.32%	2.96%	2.64%	3.15%	3.06%	3.44%

4. Обсуждение результатов работы алгоритмов

Из таблиц 3 и 4 следует, что на наборах Т₁ и Т₂ оба алгоритма существенно улучшают исходные результаты распознавания, при низком качестве оцифровки точность распознавания может быть повышена более чем на 6%. Во всех рассмотренных случаях алгоритм дает лучшие результаты, чем алгоритм .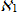

Недостатком алгоритма является использование ничем не обоснованной гипотезы о зависимости символа от двух предыдущих символов.

Недостатком алгоритма является существенно более низкое быстродействие по сравнению с быстродействием алгоритма – более чем в 100 раз. Однако необходимо отметить, что алгоритм являясь очень простым, обрабатывает одно слово примерно за 0.001 секунды.

В некоторых случаях использование триграмм приводит к ухудшению верных результатов распознавания. В основном, такие случаи  объясняются двумя следующими причинами:

• исходное распознавание дало не очень уверенный результат с низкими оценками первой альтернативы, а триграммы, получаемые из прочих альтернатив, имеют больший вес (например, в слове «ДИНАР» знакоместо с символом «Д» имеет низкую оценку, равную 0.57, и это приводит к замене на символ «Л» из-за того, что вес триграммы «ДИН» приблизительно равен  0.0001,  а вес триграммы «ЛИН» примерно равен 0.0034),
• в словаре триграмм отсутствуют триграммы, необходимые для подтверждения троек символов в редких именах, фамилиях или отчествах (например, в словаре триграмм не содержится триграммы «ЗРВ», отчего слово «АЗРВАРД» заменяется на «АЗРААРД»).

Распределение количества ошибок распознавания в зависимости от оценок распознавания после применения триграмм также выглядит «улучшенным». На рисунке 3 представлена гистограмма, подсчитанная после применения триграмм с помощью алгоритма , в сравнении с исходной гистограммой. Видно, что практически на всех интервалах оценок количество ошибок уменьшено.

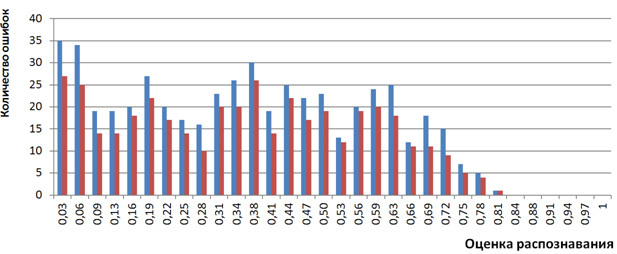
Рисунок 3. Гистограмма количества ошибок распознавания в зависимости от оценок распознавания до (синий) и после (красный) применения триграмм

Заключение

Мы показали способ коррекции распознанных документов с помощью механизма триграмм на примере  полей паспорта (ФИО) гражданина Российской Федерации. Были описаны два алгоритма такой коррекции и основные проблемы их работы. Существенным является наличие разумных оценок надежности, формируемых механизмом распознавания, и представительной выборки слов для построения словаря триграмм.

Описанные алгоритмы использованы для коррекции результатов распознавания в работающих программных продуктах Smart Engines.

Список полезных источников

1. Щуцкий Ю. К. Китайская классическая «Книга Перемен». — 2-е изд. испр. и доп. / Под ред. А. И. Кобзева. — М.: Наука, 1993.
2. Kukich, K. Techniques for Automatically Correcting Words in Text. ACM computing survey, Computational Linguistic, V. 24, No. 4, 377-439. 1992.
3. «Паспортный сканер своими руками» (https://habrahabr.ru/company/smartengines/blog/278257/)
4. «Распознавание Паспорта РФ на мобильном телефоне» (https://habrahabr.ru/company/smartengines/blog/252703/)
5. R. Cowell, P. Dawid, S. Lauritzen, D. Spiegelhalter. Probabilistic Networks and Expert Systems. Springer, 1999.
6. Michael I. Jordan. An introduction to probabilistic graphical models. Manuscript used for Class Notes of CS281A at UC Berkeley, Fall 2002.