James Kyle как-то раз взял и написал пост про структуры данных, добавив их реализацию на JavaScript. А я взял и перевёл.

Дисклеймер: в посте много ascii-графики. Не стоит его читать с мобильного устройства — вас разочарует форматирование текста.




Сегодня мы узнаем всё о структурах данных.

«Оооооой как интересно...», да?

Да уж, не самая сочная тема на сей день, однако крайне важная. Не для того, чтобы сдавать курсы наподобие CS101, а чтобы лучше разбираться в программировании.

Знание структур данных поможет вам:

• Управлять сложностью своих программ, делая их доступней для понимания.
• Создавать высокопроизводительные программы, эффективно работающие с памятью.

Я считаю, что первое важнее. Правильная структура данных может кардинально упростить код, устраняя запутанную логику.

Второй пункт тоже важен. Когда учитываются производительность или память программы, правильный выбор структуры данных значительно сказывается на работе.

Чтобы познакомиться со структурами данных, мы реализуем некоторые из них. Не беспокойтесь, код будет лаконичен. На самом деле, тут больше комментариев, а кода между ними — раз, два и обчёлся.

============================================================================
,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'
============================================================================

Что такое структуры данных?

По сути, это способы хранить и организовывать данные, чтобы эффективней решать различные задачи. Данные можно представить по-разному. В зависимости от того, что это за данные и что вы собираетесь с ними делать, одно представление подойдёт лучше других.

Чтобы понять, почему так происходит, сперва поговорим об алгоритмах.

/*** ===================================================================== *** *                                                                           *
 *                        ,--,--.    ,--,--.                                 *
 *   ,----------.        |   |   |  |   |   |            _____               *
 *  |`----------'|       |   |   |  |   |   |           |     |    ,------.  *
 *  |            |       |   |   |  |   |   |      ,--. | o o |   |`------'| *
 *  |            |      ,| +-|-+ |  | +-|-+ |`     |  | |_____|   |        | *
 *  |            | ,:==| | |###|======|###| | |====#==#====#=,,   |        | *
 *  |            | ||   `| +---+ |  | +---+ |'  ,,=#==#====O=``  ,|        | *
 *  |            | ||    |   |   |  |   |   |   ``=#==#====#=====||        | *
 *   `----------'  ||    |   |   |  |   |   |      |__|          `|        | *
 *    | | ``=| |===``    `--,',--`  `--,',--`      /||\            `------'  *
 **   \_/    \_/         / /   \ \  / /   \ \     //||\\           |_|  |_| **
\*** ===================================================================== ***/

Алгоритмы

Алгоритм — такое хитроумное название для последовательности совершаемых действий.

Структуры данных реализованы с помощью алгоритмов, алгоритмы — с помощью структур данных. Всё состоит из структур данных и алгоритмов, вплоть до уровня, на котором бегают микроскопические человечки с перфокартами и заставляют компьютер работать. (Ну да, у Интела в услужении микроскопические люди. Поднимайся, народ!)

Любая данная задача реализуется бесконечным количеством способов. Как следствие, для решения распространённых задач изобрели множество различных алгоритмов.

Например, для сортировки неупорядоченного множества элементов существует до смешного большое количество алгоритмов:

Сортировка вставками, Сортировка выбором, Сортировка слиянием, Сортировка пузырьком, Cортировка кучи, Быстрая сортировка, Сортировка Шелла, Сортировка Тима, Блочная сортировка, Поразрядная сортировка...

Некоторые из них значительно быстрее остальных. Другие занимают меньше памяти. Третьи легко реализовать. Четвёртые построены на допущениях относительно наборов данных.

Каждая из сортировок подходит лучше других для определённой задачи. Поэтому вам надо будет сперва решить, какие у вас потребности и критерии, чтобы понять, как сравнивать алгоритмы между собой.

Для сравнения производительности алгоритмов используется грубое измерение средней производительности и производительности в худшем случае, для обозначения которых используется термин «О» большое.

/*** ===================================================================== *** *           a           b                                 d                 *
 *           a         b    O(N^2)                      d                    *
 *     O(N!) a        b                O(N log N)    d                    c  *
 *           a      b                            d                 c         *
 *          a      b                          d             c        O(N)    *
 *          a    b                         d         c                       *
 *          a  b                       d      c                              *
 *         a  b                     d  c                                     *
 *         ab                   c                          O(1)              *
 *  e    e    e    e    ec   d    e    e    e    e    e     e    e    e      *
 *      ba        c      d                                                   *
 *    ba   c        d                       f    f    f    f    f    f    f  *
 ** cadf    f d    f    f    f    f    f       O(log N)                     **
\*** ===================================================================== ***/

О большое

«О» большое — обозначение способа приблизительной оценки производительности алгоритмов для относительного сравнения.

О большое — заимствованное информатикой математические обозначение, определяющее, как алгоритмы соотносятся с передаваемым им некоторым количеством N данных.

О большое характеризует две основные величины:

Оценка времени выполнения — общее количество операций, которое алгоритм проведёт на данном множестве данных.

Оценка объёма — общее количество памяти, требующееся алгоритму для обработки данного множества данных.

Оценки делаются независимо друг от друга: одни алгоритмы могут производить меньше операций, чем другие, занимая при этом больше памяти. Определив свои требования, вы сможете выбрать соответствующий алгоритм.

Вот некоторые распространённые значения О большого:

Имя               Нотация    Что вы скажете, припрись они к вам на вечеринку
----------------------------------------------------------------------------
Константная       O(1)         ОХРЕНЕННО!!
Логарифмическая   O(log N)     КРУТО!
Линейная          O(N)         НОРМАС.
Линейно-
логарифмическая   O(N log N)   БЛИИИН...
Полиномиальная    O(N ^ 2)     ОТСТОЙ
Экспоненциальная  O(2 ^ N)     ОТВРАТИТЕЛЬНО
Факториальная     O(N!)        ТВОЮЖМАТЬ

Чтобы дать представление, о каких порядках чисел мы говорим, давайте взглянем, что это будут за значения в зависимости от N.

           N = 5            10             20             30
-----------------------------------------------------------------------
O(1)           1            1              1              1
O(log N)       2.3219...    3.3219...      4.3219...      4.9068...
O(N)           5            10             20             30
O(N log N)     11.609...    33.219...      84.638...      147.204...
O(N ^ 2)       25           100            400            900
O(2 ^ N)       32           1024           1,048,576      1,073,741,824
O(N!)          120          3,628,800      2,432,902,0... 265,252,859,812,191,058,636,308,480,000,000

Как видите, даже при относительно небольших числах можно сделать *дофига* дополнительной работы.

Структуры данных позволяют производить 4 основных типа действий: доступ, поиск, вставку и удаление.

Замечу, что структуры данных могут быть хороши в одном из действий, но плохи в другом.

                          Доступ      Поиск       Вставка      Удаление
------------------------------------------------------------------------
                Массив    O(1)        O(N)        O(N)         O(N)
        Связный список    O(N)        O(N)        O(1)         O(1)
Двоичное дерево поиска    O(log N)    O(log N)    O(log N)     O(log N)

Или даже…

                          Доступ       Поиск      Вставка      Удаление
------------------------------------------------------------------------
                Массив    ОХРЕНЕННО    НОРМАС     НОРМАС       НОРМАС
        Связный список    НОРМАС       НОРМАС     ОХРЕНЕННО    ОХРЕНЕННО
Двоичное дерево поиска    КРУТО        КРУТО      КРУТО        КРУТО

Кроме того, некоторые действия имеют разную «среднюю» производительность и производительность в «самом худшем случае».

Идеальной структуры данных не существует. Вы выбираете самую подходящую, основываясь на данных и на том, как они будут обрабатываться. Чтобы сделать правильный выбор, важно знать различные распространённые структуры данных.

/*** ===================================================================== *** *                             _.-..                                         *
 *                           ,'9 )\)`-.,.--.                                 *
 *                           `-.|           `.                               *
 *                              \,      ,    \)                              *
 *                               `.  )._\   (\                               *
 *                                |//   `-,//                                *
 *                                ]||    //"                                 *
 **                        hjw    ""    ""                                  **
\*** ===================================================================== ***/

Память

Компьютерная память — довольно скучная штука. Это группа упорядоченных слотов, в которых хранится информация. Чтобы получить к ней доступ, вы должны знать её адрес в памяти.

Фрагмент памяти можно представить так:

Значения: |1001|0110|1000|0100|0101|1010|0010|0001|1101|1011...
  Адреса: 0    1    2    3    4    5    6    7    8    9    ...

Если вы задумывались, почему в языках программирования отсчёт начинается с 0 — потому, что так работает память. Чтобы прочитать первый фрагмент памяти, вы читаете с 0 до 1, второй — с 1 до 2. Адреса этих фрагментов соответственно равны 0 и 1.

Конечно же, в компьютере больше памяти, чем показано в примере, однако её устройство продолжает принцип рассмотренного шаблона.

Просторы памяти — как Дикий Запад. Каждая работающая на компьютере программа хранится внутри одной и той же *физической* структуры данных. Использование памяти — сложная задача, и для удобной работы с ней существуют дополнительные уровни абстракции.

Абстракции имеют два дополнительных назначения:

— Сохраняют данные в памяти таким образом, чтобы с ними было эффективно и/или быстро работать.

— Сохраняют данные в памяти так, чтобы их было проще использовать.

/*** ===================================================================== *** *                  *     _______________________                            *
 *                    ()=(_______________________)=()           *            *
 *       *                |                     |                            *
 *                        |   ~ ~~~~~~~~~~~~~   |       *               *    *
 *             *          |                     |                            *
 *   *                    |   ~ ~~~~~~~~~~~~~   |         *                  *
 *                        |                     |                            *
 *                        |   ~ ~~~~~~~~~~~~~   |                 *          *
 *        *               |                     |                            *
 *                   *    |_____________________|         *        *         *
 *                    ()=(_______________________)=()                        *
 **                                                                         **
\*** ===================================================================== ***/

Списки

Для начала реализуем список, чтобы показать сложности взаимодействия между памятью и структурой данных.

Список — представление пронумерованной последовательности значений, где одно и то же значение может присутствовать сколько угодно раз.

Начнём с пустого блока памяти, представленного обычным JavaScript-массивом. Также нам понадобится хранить значение длины списка.

Заметьте, что мы хотим хранить длину отдельно, поскольку в реальности у «памяти» нет значения length, которое можно было бы взять и прочитать.

class List {

    constructor() {
        this.memory = [];
        this.length = 0;
    }

    //...
}

Первым делом нужно получать данные из списка. Обычный список позволяет очень быстро получить доступ к памяти, поскольку вы уже знаете нужный адрес.

Сложность операции доступа в список — O(1) — «ОХРЕНЕННО!!»

get(address) {
    return this.memory[address];
}

У списков есть порядковые номера, поэтому можно вставлять значения в начало, середину и конец.

Мы сфокусируемся на добавлении и удалении значений в начало или конец списка. Для этого понадобятся 4 метода:

• Push — Добавить значение в конец.
• Pop — Удалить значение из конца.
• Unshift — Добавить значение в начало.
• Shift — Удалить значение из начала.

Начнём с операции «push» — реализуем добавление элементов в конец списка.

Это настолько же легко, как добавить значение в адрес, следующий за нашим списком. Поскольку мы храним длину, вычислить адрес — проще простого. Добавим значение и увеличим длину.

Добавление элемента в конец списка — константа O(1) — «ОХРЕНЕННО!!»

push(value) {
    this.memory[this.length] = value;
    this.length++;
}

Комментарии хабра: poxu не согласен с автором и объясняет, что существует операция расширения памяти, увеличивающая сложность добавления элементов в список.

Далее, реализуем метод «pop», убирающий элемент из конца нашего списка. Аналогично push, всё, что нужно сделать — убрать значение из последнего адреса. Ну, и уменьшить длину.

Удаление элемента из конца списка — константа O(1) — «ОХРЕНЕННО!!»

pop() {
    // Нет элементов — ничего не делаем.
    if (this.length === 0) return;

    // Получаем последнее значение, перестаём его хранить, возвращаем его.
    var lastAddress = this.length - 1;
    var value = this.memory[lastAddress];
    delete this.memory[lastAddress];
    this.length--;

    // Возвращаем значение, чтобы его можно было использовать.
    return value;
}

«Push» и «pop» работают с концом списка, и в общем-то являются простыми операциями, поскольку не затрагивают весь остальной список.

Давайте посмотрим, что происходит, когда мы работаем с началом списка, с операциями «unshift» и «shift».

Чтобы добавить новый элемент в начало списка, нужно освободить пространство для этого значения, сдвинув на один все последующие значения.

[a, b, c, d, e]
 0  1  2  3  4
  ?  ?  ?  ?  ?
    1  2  3  4  5
[x, a, b, c, d, e]

Чтобы сделать такой сдвиг, нужно пройтись по каждому из элементов и поставить на его место предыдущий.

Поскольку мы вынуждены пройтись по каждому из элементов списка:

Добавление элемента в начало списка — линейно O(N) — «НОРМАС.»

unshift(value) {
    // Cохраняем значение, которое хотим добавить в начало.
    var previous = value;

    // Проходимся по каждому элементу...
    for (var address = 0; address < this.length; address++) {
        // заменяя текущее значение «current» на предыдущее значение «previous»,
        // и сохраняя значение «current» для следующей итерации.
        var current = this.memory[address];
        this.memory[address] = previous;
        previous = current;
    }

    // Добавляем последний элемент на новую позицию в конце списка.
    this.memory[this.length] = previous;
    this.length++;
}

Осталось написать функцию сдвига списка в противоположном направлении — shift.

Мы удаляем первое значение и затем сдвигаем каждый элемент списка на предшествующий адрес.

[x, a, b, c, d, e]
    1  2  3  4  5
  ?  ?  ?  ?  ?
 0  1  2  3  4
[a, b, c, d, e]

Удаление элемента из начала списка — линейно O(N) — «НОРМАС.»

shift() {
    // Нет элементов — ничего не делаем.
    if (this.length === 0) return;

    var value = this.memory[0];

    // Проходимся по каждому элементу, кроме последнего
    for (var address = 0; address < this.length - 1; address++) {
        // и заменяем его на следующий элемент списка.
        this.memory[address] = this.memory[address + 1];
    }

    // Удаляем последний элемент, поскольку значение теперь в предыдущем адресе.
    delete this.memory[this.length - 1];
    this.length--;

    return value;
}

Списки отлично справляются с быстрым доступом к элементам в своём конце и работой с ними. Однако, как мы увидели, для элементов из начала или середины они не слишком хороши, так как приходится вручную обрабатывать адреса памяти.

Давайте посмотрим на иную структуру данных и её методы по добавлению, доступу и удалению значений без необходимости знать адреса элементов.

/*** ===================================================================== *** *                           ((\                                             *
 *     (              _  ,-_  \ \                                            *
 *     )             / \/  \ \ \ \                                           *
 *     (            /)| \/\ \ \| |          .'---------------------'.        *
 *     `~()_______)___)\ \ \ \ \ |        .'                         '.      *
 *                 |)\ )  `' | | |      .'-----------------------------'.    *
 *                /  /,          |      '...............................'    *
 *        ejm     |  |          /         \   _____________________   /      *
 *                \            /           | |_)                 (_| |       *
 *                 \          /            | |                     | |       *
 *                  )        /             | |                     | |       *
 **                /       /              (___)                   (___)     **
\*** ===================================================================== ***/

Хеш-таблицы

Хеш-таблица — неупорядоченная структура данных. Вместо индексов мы работаем с «ключами» и «значениями», вычисляя адрес памяти по ключу.

Смысл в том, что ключи «хешируются» и позволяют эффективно работать с памятью — добавлять, получать, изменять и удалять значения.

var hashTable = new HashTable();

hashTable.set('myKey', 'myValue');
hashTable.get('myKey'); // >> 'myValue'

Вновь используем обычный JavaScript-массив, представляющий память.

class HashTable {

    constructor() {
        this.memory = [];
    }

    // ...
}

Чтобы сохранять пары ключ-значение из хеш-таблицы в память, нужно превращать ключи в адреса. Этим занимается операция «хеширования».

Она принимает на вход ключ и преобразовывает его в уникальное число, соответствующее этому ключу.

hashKey("abc") =>  96354
hashKey("xyz") => 119193

Такая операция требует осторожности. Если ключ слишком большой, он будет сопоставляться несуществующему адресу в памяти.

Следовательно, хеш-функция должна ограничивать размер ключей, т.е. ограничивать число доступных адресов памяти для неограниченного количества значений.

Любая реализация хеш-таблиц сталкивается с этой проблемой.

Однако, поскольку мы собираемся рассмотреть лишь устройство их работы, предположим, что коллизий не случится.

Давайте определим функцию «hashKey».

Не вдавайтесь во внутреннюю логику, просто поверьте, что она принимает на вход строку и возвращает (практически всегда) уникальный адрес, который мы будем использовать в остальных функциях.

hashKey(key) {
    var hash = 0;
    for (var index = 0; index < key.length; index++) {
          // Ма-а-а-агия.
          var code = key.charCodeAt(index);
        hash = ((hash << 5) - hash) + code | 0;
    }
    return hash;
}

Теперь определим функцию «get», получающую значение по ключу.

Сложность чтения значения из хеш-таблицы — константа O(1) — «ОХРЕНЕННО!!»

get(key) {
    // Сперва получим адрес по ключу.
    var address = this.hashKey(key);
    // Затем просто вернём значение, находящееся по этому адресу.
    return this.memory[address];
}

Перед тем, как получать данные, неплохо бы их сперва добавить. В этом нам поможет функция «set».

Сложность установки значения в хеш-таблицу — константа O(1) — «ОХРЕНЕННО!!»

set(key, value) {
    // И вновь начинаем с превращения ключа в адрес.
    var address = this.hashKey(key);
    // Затем просто записываем значение по этому адресу.
    this.memory[address] = value;
}

Наконец, нужен способ удалять значения из хеш-таблицы. Сложность удаления значения из хеш-таблицы — константа O(1) — «ОХРЕНЕННО!!»

remove(key) {
    // Как обычно, хешируем ключ, получая адрес.
    var address = this.hashKey(key);
    // Удаляем значение, если оно существует.
    if (this.memory[address]) {
        delete this.memory[address];
    }
}

============================================================================
,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'
============================================================================

Теперь мы прекратим работать с памятью напрямую: все последующие структуры данных будут реализовываться через другие структуры данных.

Новые структуры фокусируются на двух вещах:

• Организовывают данные, исходя из особенностей их применения
• Абстрагируют детали реализации

Цель таких структур данных — организовать информацию для применения в программах различного типа. Они предоставляют язык, позволяющий выражать более сложную логику. При этом абстрагируются детали реализации, т.е. можно изменить реализацию, сделав её быстрее.

/*** ===================================================================== *** *                             _ . - - -- .. _                               *
 *         ||||            .-'      /```\     `'-_             /|            *
 *         ||||           (     /`` \___/ ```\    )           | |            *
 *         \__/           |`"-//..__     __..\\-"`|           | |            *
 *          ||            |`"||...__`````__...||"`|           | |            *
 *          ||            |`"||...__`````__...||"`|           \ |            *
 *          ||       _,.--|`"||...__`````__...||"`|--.,_       ||            *
 *          ||    .'`     |`"||...__`````__...||"`|     `'.    ||            *
 *          ||   '.        `/ |...__`````__...| \         .'   ||            *
 *          ||     `'-..__  ``      `````      ``  __..-'`     ||            *
 *                        `""---,,,_______,,,---""`                          *
 **                                                                         **
\*** ===================================================================== ***/

Стеки

Стеки похожи на списки. Они также упорядочены, но ограничены в действиях: можно лишь добавлять и убирать значения из конца списка. Как мы увидели ранее, это происходит очень быстро, если обращаться к памяти напрямую.

Однако стеки могут быть реализованы через другие структуры данных, чтобы получить дополнительную функциональность.

Наиболее общий пример использования стеков — у вас есть один процесс, добавляющий элементы в стек и второй, удаляющий их из конца — приоритизируя недавно добавленные элементы.

Нам вновь понадобится JavaScript-массив, но на этот раз он символизирует не память, а список, вроде реализованного выше.

class Stack {

    constructor() {
        this.list = [];
        this.length = 0;
    }

    // ...
}

Нам понадобится реализовать два метода, функционально идентичных методам списка — «push» и «pop».

Push добавляет элементы на верхушку стека.

push(value) {
    this.length++;
    this.list.push(value);
}

Pop удаляет элементы из верхушки.

pop() {
    // Нет элементов — ничего не делаем.
    if (this.length === 0) return;

    // Возьмём последний элемент списка и вернём значение.
    this.length--;
    return this.list.pop();
}

Кроме того, добавим функцию peek, показывающую элемент на верхушке стека без его удаления. Прим. переводчика: peek – взглянуть.

peek() {
    // Возвращаем последний элемент, не удаляя его.
    return this.list[this.length - 1];
}

/*** ===================================================================== *** *                   /:""|                     ,@@@@@@.                      *
 *                  |: oo|_                   ,@@@@@`oo                      *
 *                  C     _)                  @@@@C   _)                     *
 *                    ) /                     "@@@@ '=                       *
 *                   /`\\                      ```)/                         *
 *                  || | |                       /`\\                        *
 *                  || | |                      || | \                       *
 *                  ||_| |                      || | /                       *
 *                  \( ) |                      ||_| |                       *
 *               |~~~`-`~~~|                    |))) |                       *
 *         (_)   |         |         (_)        |~~~/          (_)           *
 *         | |`""....__     __....""`| |`""...._|| /  __....""`| |           *
 *         | |`""....__`````__....""`| |`""....__`````__....""`| |           *
 *         | |       | ||```         | |        ||`|``         | |           *
 *         | |       |_||__          | |        ||_|__         | |           *
 *        ,| |, jgs  (____))        ,| |,       ((;:;:)       ,| |,          *
 **       `---`                     `---`                     `---`         **
\*** ===================================================================== ***/

Очереди

Теперь создадим очередь — структуру, комплементарную стеку. Разница в том, что элементы очереди удаляются из начала, а не из конца, т.е. сначала старые элементы, потом новые.

Как уже оговаривалось, поскольку функциональность ограничена, существуют разные реализации очереди. Хорошим способом будет использование связного списка, о котором мы поговорим чуть позже.

И вновь мы призываем на помощь JavaScript-массив! В случае с очередью мы опять рассматриваем его как список, а не как память.

class Queue {

    constructor() {
        this.list = [];
        this.length = 0;
    }

    // ...
}

Аналогично стекам мы определяем две функции для добавления и удаления элементов из очереди.

Первым будет «enqueue» — добавление элемента в конец списка.

enqueue(value) {
    this.length++;
    this.list.push(value);
}

Далее — «dequeue». Элемент удаляется не из конца списка, а из начала.

dequeue() {
    // Нет элементов — ничего не делаем.
    if (this.length === 0) return;

    // Убираем первый элемент методом shift и возвращаем значение.
    this.length--;
    return this.list.shift();
}

Аналогично стекам объявим функцию «peek», позволяющую получить значение в начале очереди без его удаления.

peek() {
    return this.list[0];
}

Важно заметить, что, поскольку для реализации очереди использовался список, она наследует линейную производительность метода shift (т.е. O(N) — «НОРМАС.»).

Как мы увидим позже, связные списки позволяют реализовать более быструю очередь.

============================================================================
,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'
============================================================================

С этого места и далее мы будем работать со структурами данных, где значения ссылаются друг на друга.

+- Структура данных -------------------------------------+
|  +- Элемент A ------------+ +- Элемент B ------------+ |
|  | Значение: 1            | | Значение: 2            | |
|  | Ссылка на: (Элемент B) | | Ссылка на: (Элемент A) | |
|  +------------------------+ +------------------------+ |
+--------------------------------------------------------+

Элементы структуры данных становятся сами по себе министруктурами, содержащими значение и дополнительную информацию — ссылки на другие элементы родительской структуры.

Сейчас вы поймёте, что я имею ввиду.

/*** ===================================================================== *** *                                                                           *
 *   |                                 RICK ASTLEY'S NEVER GONNA...          *
 *   |       +-+                                                             *
 *   |  +-+  |-|                          [^] - GIVE YOU UP                  *
 *   |  |^|  |-|                 +-+      [-] - LET YOU DOWN                 *
 *   |  |^|  |-|       +-+       |*|      [/] - RUN AROUND AND DESERT YOU    *
 *   |  |^|  |-|  +-+  |\|       |*|      [\] - MAKE YOU CRY                 *
 *   |  |^|  |-|  |/|  |\|  +-+  |*|      [.] - SAY GOODBYE                  *
 *   |  |^|  |-|  |/|  |\|  |.|  |*|      [*] - TELL A LIE AND HURT YOU      *
 *   |  |^|  |-|  |/|  |\|  |.|  |*|                                         *
 *   +--------------------------------                                       *
 **                                                                         **
\*** ===================================================================== ***/

Графы

На самом деле граф — совсем не то, о чём вы подумали, увидев ascii-график.

Граф — структура наподобие этой:



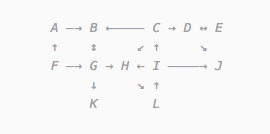
У нас есть множество «вершин» (A, B, C, D, ...), связанных линиями.

Эти вершины можно представить вот так:

Node {
    value: ...,
    lines: [(Node), (Node), ...]
}

А весь граф будет выглядеть вот так:

Graph {
    nodes: [
        Node {...},
        Node {...},
        ...
    ]
}

Представим список вершин JavaScript-массивом. Массив используется не с целью специально упорядочить вершины, а как место для хранения вершин.

class Graph {

    constructor() {
        this.nodes = [];
    }

    // ...
}

Начнём добавлять значения в граф, создавая вершины без каких-либо линий.

addNode(value) {
    this.nodes.push({
        value: value,
        lines: []
    });
}

Теперь нужен способ искать вершины в графе. Обычно для ускорения поиска делается ещё одна структура данных поверх графа.

Но в нашем случае мы просто переберём все вершины, чтобы найти соответствующую значению. Способ медленный, но работающий.

find(value) {
    return this.nodes.find(function(node) {
        return node.value === value;
    });
}

Теперь мы можем связать две вершины, проведя «линию» от одной до другой (прим. переводчика: дугу графа).

addLine(startValue, endValue) {
    // Найдём вершины для каждого из значений.
    var startNode = this.find(startValue);
    var endNode = this.find(endValue);

    // Ругнёмся, если не нашли одной или другой.
    if (!startNode || !endNode) {
        throw new Error('Обе вершины должны существовать');
    }

    // В стартовую вершину startNode добавим ссылку на конечную вершину endNode.
    startNode.lines.push(endNode);
}

Полученный граф можно использовать вот так:

var graph = new Graph();
graph.addNode(1);
graph.addNode(2);
graph.addLine(1, 2);
var two = graph.find(1).lines[0];

Кажется, что для такой мелкой задачи сделано слишком много работы, однако это мощный паттерн.

Он часто применяется для поддержания прозрачности в сложных программах. Это достигается оптимизацией взаимосвязей между данными, а не операций над самими данными. Если вы выберете одну вершину в графе, невероятно просто найти связанные с ней элементы.

Графами можно представлять уйму вещей: пользователей и их друзей, 800 зависимостей в папке node_modules, даже сам интернет, являющийся графом связанных друг с другом ссылками веб-страниц.

/*** ===================================================================== *** *      _______________________                                              *
 *  ()=(_______________________)=()              ,-----------------,_        *
 *      |                     |               ,"                      ",     *
 *      |   ~ ~~~~~~~~~~~~~   |             ,'    ,---------------,     `,   *
 *      |               ,----------------------------,          ,----------- *
 *      |   ~ ~~~~~~~~ |                              |        |             *
 *      |               `----------------------------'          `----------- *
 *      |   ~ ~~~~~~~~~~~~~   |            `,    `----------------'     ,'   *
 *      |                     |              `,                      ,'      *
 *      |_____________________|                 `------------------'         *
 *  ()=(_______________________)=()                                          *
 **                                                                         **
\*** ===================================================================== ***/

Связные списки

Давайте теперь посмотрим, как графоподобная структура может оптимизировать упорядоченный список данных.

Связные списки — распространённая структура данных, зачастую используемая для реализации других структур. Преимущество связного списка — эффективность добавления элементов в начало, середину и конец.

Связный список по своей сути похож на граф: вы работаете с вершинами, указывающими на другие вершины. Они расположены таким образом:

1 -> 2 -> 3 -> 4 -> 5

Если представить эту структуру в виде JSON, получится нечто такое:

{
    value: 1,
    next: {
        value: 2,
        next: {
            value: 3,
            next: {...}
        }
    }
}

В отличие от графа, связный список имеет единственную вершину, из которой начинается внутренняя цепочка. Её называют «головой», головным элементом или первым элементом связного списка.

Также мы собираемся отслеживать длину списка.

class LinkedList {

    constructor() {
        this.head = null;
        this.length = 0;
    }

    // ...
}

Первым делом нужен способ получать значение по данной позиции.

В отличие от обычных списков мы не можем перепрыгнуть на нужную позицию. Вместо этого мы должны перейти к ней через отдельные вершины.

get(position) {
    // Выведем ошибку, если искомая позиция превосходит число вершин в списке.
    if (position >= this.length) {
        throw new Error('Позиция выходит за пределы списка');
    }

    // Начнём с головного элемента списка.
    var current = this.head;

    // Пройдём по всем элементам при помощи node.next,
    // пока не достигнем требуемой позиции.
    for (var index = 0; index < position; index++) {
        current = current.next;
    }

    // Вернём найденную вершину.
    return current;
}

Теперь необходим способ добавлять вершины в выбранную позицию.

Создадим метод add, принимающий значение и позицию.

add(value, position) {
    // Сначала создадим вершину, содержащую значение.
    var node = {
        value: value,
        next: null
    };

    // Нужно обработать частный случай, когда вершина вставляется в начало.
    // Установим поле «next» в текущий головной элемент и заменим
    // головной элемент нашей вершиной.
    if (position === 0) {
        node.next = this.head;
        this.head = node;

    // Если мы добавляем вершину на любую другую позицию, мы должны вставить её
    // между текущей вершиной current и предыдущей previous.
    } else {
          // Сперва найдём предыдущую и текущую вершины.
          var prev = this.get(position - 1);
          var current = prev.next;
          // Затем вставим новую вершину между ними, установив поле «next»
          // на текущую вершину current,
          // и поле «next» предыдущей вершины previous — на вставляемую.
          node.next = current;
          prev.next = node;
    }

    // И увеличим длину.
    this.length++;
}

Последний метод, который нам понадобится — remove. Найдём вершину по позиции и выкинем её из цепочки.

remove(position) {
    // Если мы удаляем головной элемент, просто переставим указатель head
    // на следующую вершину.
    if (position === 0) {
        this.head = this.head.next;

    // Для остальных случаев требуется найти предыдущую вершину и поставить
    // в ней ссылку на вершину, следующую за текущей.
    } else {
        var prev = this.get(position - 1);
        prev.next = prev.next.next;
    }

    // И затем уменьшим длину.
    this.length--;
}

============================================================================
,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'
============================================================================

Две оставшиеся структуры данных относятся к семейству «деревьев».

Как и в жизни, существует множество различных древовидных структур данных.

Прим. переводчика: ну не-е-е-е, я пас…

Binary Trees:
AA Tree, AVL Tree, Binary Search Tree, Binary Tree, Cartesian Tree, left child/right sibling tree, order statistic tree, Pagoda,…

B Trees:
B Tree, B+ Tree, B* Tree, B Sharp Tree, Dancing Tree, 2-3 Tree,…

Heaps:
Heap, Binary Heap, Weak Heap, Binomial Heap, Fibonacci Heap, Leonardo Heap, 2-3 Heap, Soft Heap, Pairing Heap, Leftist Heap, Treap,…

Trees:
Trie, Radix Tree, Suffix Tree, Suffix Array, FM-index, B-trie,…

Multi-way Trees:
Ternary Tree, K-ary tree, And-or tree, (a,b)-tree, Link/Cut Tree,…

Space Partitioning Trees:
Segment Tree, Interval Tree, Range Tree, Bin, Kd Tree, Quadtree, Octree, Z-Order, UB-Tree, R-Tree, X-Tree, Metric Tree, Cover Tree,…

Application-Specific Trees:
Abstract Syntax Tree, Parse Tree, Decision Tree, Minimax Tree,…

Чего уж вы не ожидали, так это что будете изучать сегодня дендрологию… И это ещё не все деревья. Пусть они вас не смущают, большинство из них вообще не имеет смысла. Надо же было людям как-то защищать кандидатские степени и что-то для этого доказывать.

Деревья похожи на графы или связные списки, с той разницей, что они «однонаправленые». Это значит, что в них не может существовать циклических ссылок.



Если вы можете пройти круг по вершинам дерева… что ж, поздравляю, но это не дерево.

Деревья применяются во множестве задач. Они используются для оптимизации поиска или сортировки. Они могут лучше организовывать программу. Они могут создать представление, с которым проще работать.

/*** ===================================================================== *** *            ccee88oo             \ | /                                     *
 *          C8O8O8Q8PoOb o8oo    '-.;;;.-,   ooooO8O8QOb o8bDbo              *
 *        dOB69QO8PdUOpugoO9bD  -==;;;;;==-aadOB69QO8PdUOpugoO9bD            *
 *       CgggbU8OU qOp qOdoUOdcb .-';;;'-.  CgggOU ddqOp qOdoUOdcb           *
 *           6OuU  /p u gcoUodpP   / | \ jgs  ooSec cdac pdadfoof            *
 *             \\\//  /douUP         '         \\\d\\\dp/pddoo               *
 *               \\\////                         \\ \\////                   *
 *                |||/\                           \\///                      *
 *                |||\/                           ||||                       *
 *                |||||                          /|||                        *
 ** .............//||||\.......................//|||\\..................... **
\*** ===================================================================== ***/

Деревья

Начнём с простой древовидной структуры. В ней нет особых правил, и выглядит она примерно так:

Tree {
    root: {
        value: 1,
        children: [{
            value: 2,
            children: [...]
        }, {
            value: 3,
            children: [...]
        }]
    }
}

Дерево должно начинаться с единственного родителя, «корня» дерева.

class Tree {

    constructor() {
        this.root = null;
    }

    // ...
}

Нам нужен способ обходить наше дерево и вызывать определённую функцию в каждой его вершине.

traverse(callback) {
    // Определим функцию обхода walk, которую можно рекурсивно вызывать
    // в каждой вершине дерева.
    function walk(node) {
        // Сперва вызовем callback на самой вершине.
        callback(node);
        // Затем рекурсивно вызовем walk на всех её потомках.
        node.children.forEach(walk);
    }

    // А теперь запустим процесс обхода.
    walk(this.root);
}

Теперь нужен способ добавлять вершины в дерево.

add(value, parentValue) {
    var newNode = {
        value: value,
        children: []
    };

    // Если корня не существует, установим в него новую вершину.
    if (this.root === null) {
        this.root = newNode;
        return;
    }

    // В остальных случаях переберём внутреннее дерево, найдём вершину
    // с соответствующим значением parentValue и добавим новую вершину
    // к его потомкам.
    this.traverse(function(node) {
        if (node.value === parentValue) {
            node.children.push(newNode);
        }
    });
}

Это простое дерево, возможно, полезное лишь в случае, когда отображаемые данные на него похожи.

Однако при наличии дополнительных правил деревья могут выполнять кучу различных задач.

/*** ===================================================================== *** * 0 0 1 0 1 0 0 1 0 1 1 1 0 1  ,@@@@@@@@@@@@@@,   0 0 1 0 1 0 0 1 0 1 1 1 0 *
 * 0 1 0 1 0 1 0 1 1 0 1 1 0  @@`              '@@   0 1 0 1 0 1 1 0 1 0 1 0 *
 * 1 1 0 0 0 1 0 0 1 1 1 0  @@`   8O8PoOb o8o    '@@   0 0 1 0 0 1 0 0 1 1 1 *
 * 0 0 1 1 0 1 0 1 0 0 0  @@   dOB69QO8PdUgoO9bD    @@   1 0 1 1 0 1 0 1 0 0 *
 * ===================== @@   CgbU8OU qOp qOdOdcb    @@  0 1 1 0 1 0 1 0 1 0 *
 *                       @@      6OU /p u gcoUpP     @@  1 0 1 1 0 1 0 0 1 1 *
 * ===================== @@         \\// /doP        @@  0 1 1 0 0 1 0 0 1 0 *
 * 1 1 0 0 1 1 0 1 1 0 0  @@         \\//           @@   1 0 1 0 0 1 1 0 1 1 *
 * 0 1 1 0 1 0 1 1 0 1 1 0  @@,      |||          ,@@  0 1 1 0 1 1 0 0 1 0 1 *
 * 1 0 1 0 1 1 0 0 1 0 0 1 0  @@,   //|\       ,@@   0 1 0 1 0 1 1 0 0 1 1 0 *
 **  1 0 1 0 0 1 1 0 1 0 1 0 1  `@@@@@@@@@@@@@@'   0 1 1 1 0 0 1 0 1 0 1 1  **
\*** ===================================================================== ***/

Двоичные деревья поиска

Двоичные деревья поиска — распространённая форма деревьев. Они умеют эффективно читать, искать, вставлять и удалять значения, сохраняя при этом отсортированный порядок.

Представьте, что у вас есть последовательность чисел:

1  2  3  4  5  6  7

Развернём её в дерево, начинающееся из центра.

             4
          /            2           6
     /   \       /       1     3     5     7
   -^--^--^--^--^--^--^-
    1  2  3  4  5  6  7

Вот пример, как работает бинарное дерево. У каждой вершины есть два потомка:

• Левый — меньше, чем значение вершины-родителя.
• Правый – больше, чем значение вершины-родителя.

Замечание: для того, чтобы это работало, все значения в дереве должны быть уникальны.

Это делает обход дерева при поиске значения очень эффективным. Например, попробуем найти число 5 в нашем дереве.

            (4)         <--- 5 > 4, двигаемся направо.
          /            2         (6)    <--- 5 < 6, двигаемся налево.
     /   \      /       1     3    (5)   7  <--- Мы добрались до 5!

Заметьте, чтобы добраться до 5, потребовалось сделать лишь 3 проверки. А если бы дерево состояло из 1000 элементов, путь был бы таким:

500 -> 250 -> 125 -> 62 -> 31 -> 15 -> 7 -> 3 -> 4 -> 5

Всего 10 проверок на 1000 элементов!

Ещё одной важной особенностью двоичных деревьев поиска является их схожесть со связными списками — при добавлении или удалении значения вам нужно обновлять лишь непосредственно окружающие элементы.

Как и в прошлой секции, сперва нужно установить “корень” двоичного дерева поиска.

class BinarySearchTree {

    constructor() {
        this.root = null;
    }

    // ...
}

Чтобы проверить, находится ли значение в дереве, нужно провести поиск по дереву.

contains(value) {
    // Начинаем с корня.
    var current = this.root;

    // Мы будем продолжать обход, пока есть вершины, которые можно посетить.
    // Если мы достигнем левой или правой вершин, равных null, цикл закончится.
    while (current) {

        // Если значение value больше current.value, двигаемся вправо.
        if (value > current.value) {
            current = current.right;

        // Если значение value меньше current.value, двигаемся влево.
        } else if (value < current.value) {
            current = current.left;

        // Иначе значения должны быть равны и мы возвращаем true.
        } else {
            return true;
        }
    }

    // Если мы не нашли ничего, возвращаем false.
    return false;
}

Чтобы добавить элемент в дерево, нужно произвести такой же обход, как и раньше, перепрыгивая по левым и правым вершинам в зависимости от того, больше или меньше ли они по сравнению с добавляемым значением.

Однако теперь, когда мы доберёмся до левой или правой вершины, равной null,
мы добавим вершину в эту позицию.

add(value) {
    // Для начала создадим вершину.
    var node = {
        value: value,
        left: null,
        right: null
    };

    // Частный случай, если не существует корневой вершины — добавим её.
    if (this.root === null) {
        this.root = node;
        return;
    }

    // Начнём обход с корня.
    var current = this.root;

    // Мы собираемся циклически продолжать работу до тех пор, пока не добавим
    // наш элемент или не обнаружим, что он уже находится в дереве.
    while (true) {

        // Если значение value больше current.value, двигаемся вправо.
        if (value > current.value) {

            // Если правая вершина не существует, установим её и закончим обход.
            if (!current.right) {
                current.right = node;
                break;
            }

            // Иначе перейдём на правую вершину и продолжим.
            current = current.right;

        // Если значение value меньше current.value, двигаемся влево.
        } else if (value < current.value) {

            // Если левая вершина не существует, установим её и закончим обход.
            if (!current.left) {
                current.left = node;
                break;
            }

            // Иначе перейдём на левую вершину и продолжим.
            current = current.left;

        // Если значение ни больше и не меньше, оно должно быть совпадать
        // с текущим, значит ничего делать не надо.
        } else {
            break;
        }
    }
}

/*** ===================================================================== *** *                                           .''.                            *
 *                 .''.             *''*    :_\/_:     .                     *
 *                :_\/_:   .    .:.*_\/_*   : /\ :  .'.:.'.                  *
 *            .''.: /\ : _\(/_  ':'* /\ *  : '..'.  -=:o:=-                  *
 *           :_\/_:'.:::. /)\*''*  .|.* '.\'/.'_\(/_'.':'.'                  *
 *           : /\ : :::::  '*_\/_* | |  -= o =- /)\    '  *                  *
 *            '..'  ':::'   * /\ * |'|  .'/.\'.  '._____                     *
 *                *        __*..* |  |     :      |.   |' .---"|             *
 *                 _*   .-'   '-. |  |     .--'|  ||   | _|    |             *
 *              .-'|  _.|  |    ||   '-__  |   |  |    ||      |             *
 *              |' | |.    |    ||       | |   |  |    ||      |             *
 * _____________|  '-'     '    ""       '-'   '-.'    '`      |____________ *
 ** jgs~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ **
\*** ===================================================================== ***/

Конец

Надеюсь, вы получили хорошую дозу знаний. Если вам понравилось,
ставьте звездочки в репозитории и подписывайтесь на меня в твиттере.

Также можете прочитать другую мою статью, «The Super Tiny Compiler» github.com/thejameskyle/the-super-tiny-compiler

// Экспортируем модули для тестов...
module.exports = {
    List: List,
    HashTable: HashTable,
    Stack: Stack,
    Queue: Queue,
    Graph: Graph,
    LinkedList: LinkedList,
    Tree: Tree,
    BinarySearchTree: BinarySearchTree
};

---

Также эту статью можно прочитать на гитхабе.

Перевод: aalexeev, редактура: iamo0, Чайка Чурсина.