Переменная величина – атрибут (свойство) системы, меняющий свое числовое значение. Множество значений переменой величины может иметь вид:

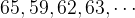
Человек анализирует числовые данные такого рода и принимает решения. Знание температуры воздуха помогает правильно одеться. Курс валюты говорит покупать ее или продавать.

Когда значений одно или несколько, то никаких трудностей не возникает. Но когда значений десятки или сотни, то человеку сложно сразу понять, что означают полученные данные. На помощь приходят интегральные характеристики множеств значений и визуализация.

Одна из интегральных характеристик множества значений переменной величины – среднее арифметическое. Посмотрим на него с точки зрения статистики, физики (механики) и эстетики.

Среднее арифметическое двух чисел

Начнем с минимального набора чисел, для которых можно подсчитать среднее арифметическое. Вот два числа:

Их среднее арифметическое:

Два наблюдения:

• Среднее арифметическое находится посередине двух чисел (больше меньшего, но меньше большего).
• Среднее арифметическое не всегда входит в анализируемый набор чисел (не равно ни одному из двух чисел).

Физический смысл среднего арифметического

Изобразим два исходных числа и их среднее арифметическое на числовой оси:

Числа помечены черными кружками, а среднее арифметическое красным треугольником. Полученная конструкция – это весы. Для весов в равновесии правило рычага требует, чтобы моменты сил были равны. Весы не наклоняются ни в одну, ни в другую сторону, так как крутящий момент отсутствует.

В механике момент силы – это произведение силы F на расстояние l:

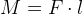
На плечи весов действует сила, создаваемая весом точек-"грузов". Обозначив расстояния от грузов до точки опоры l₁ и l₂, получим:

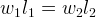
Точки-"грузы" отличаются только координатой на оси. Будем считать их вес одинаковым. Тогда:

Обозначив m координату точки опоры весов, получим:

Аналогично из формулы равенства моментов для произвольного количества N точек-"грузов" с одинаковым весом w выводится формула среднего арифметического. Равенство моментов для обоих плеч весов:

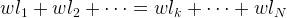
Координата опоры весов m:

Формула среднего арифметического дает координату точки опоры весов, находящихся в равновесии.

Визуальное восприятие равновесия

Равновесие в изобразительном искусстве играет важнейшую роль. Если при создании картины не достигнуто равновесие ее элементов, то произведение не будет законченным. В каждой картине художник создает равновесие различных визуальных сил.

Рудольф Арнхейм отмечает, что человеческое зрение способно обнаруживать малейшие отклонения от центра равновесия в изображении:

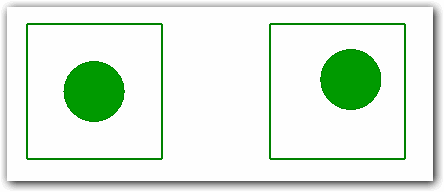
На приведенном примере слева круг находится в состоянии равновесия, а справа нет. Несмотря на то, что точка равновесия (центр квадрата) никак не отмечена на рисунке, человек с большой точностью может определить, находится ли круг в этой точке или нет.

Несмотря на то, что точка равновесия может быть не изображена, человек воспринимает ее как часть визуальной структуры:

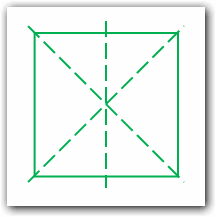
Аналогично и среднее арифметическое: необязательно входит в набор чисел, но значимо для его восприятия и оценки.

Математическое ожидание случайной величины

Для случайной величины аналогом среднего арифметического служит математическое ожидание. Вероятность при этом можно считать весом точки-"груза". Формула равенства моментов с разными весами:

Теперь точка опоры весов в равновесии это ?:

Сумма всех вероятностей равна 1. Следовательно, и сумма весов равна 1. Тогда формула координаты точки весов в равновесии равна:

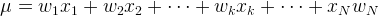
Это и есть формула математического ожидания.

Гистограмма

Гистограмма – это визуализация (геометрическое изображение) значений переменной величины с учетом вероятностей. Гистограмма показывает для выборки значений, какие из них появляются часто, какие реже, а какие совсем редко.

На гистограмме возможные значения откладываются по горизонтальной оси, а веса – по вертикальной. Диапазон значений по вертикали очевиден – от 0 до 1 (значения вероятности). По горизонтали диапазон должен включать ожидаемые значения переменной.

Гистограмма представляет собой простую картину (экземпляр изобразительного искусства). Зритель ожидает, что точка равновесия множества значений будет ровно посередине гистограммы:

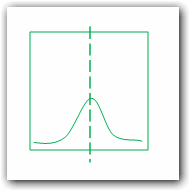
Исходя из этого должен подбираться диапазон значений для горизонтальной оси гистограммы. Тогда сразу будет видно отклонение свойств выборки значений от ожидаемых:

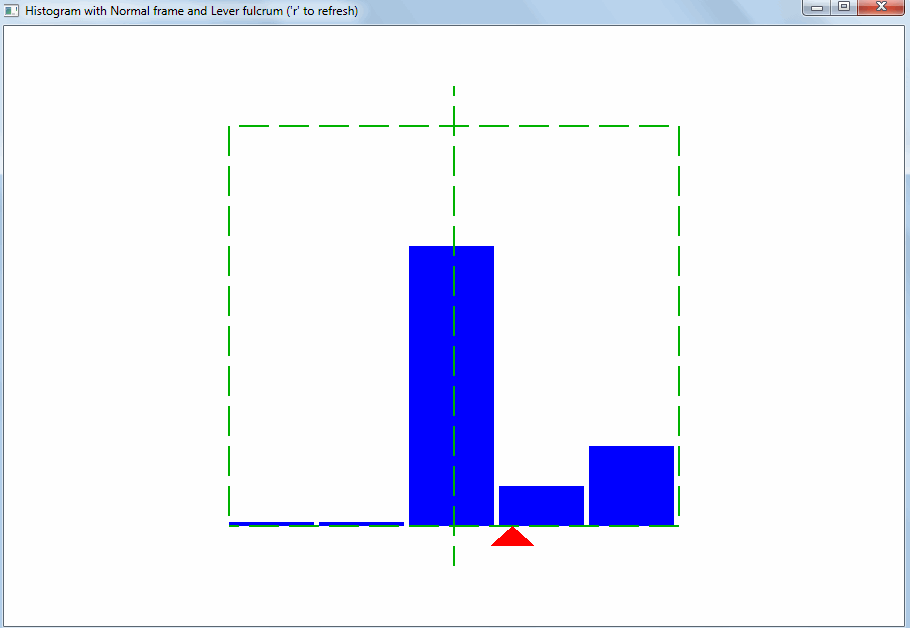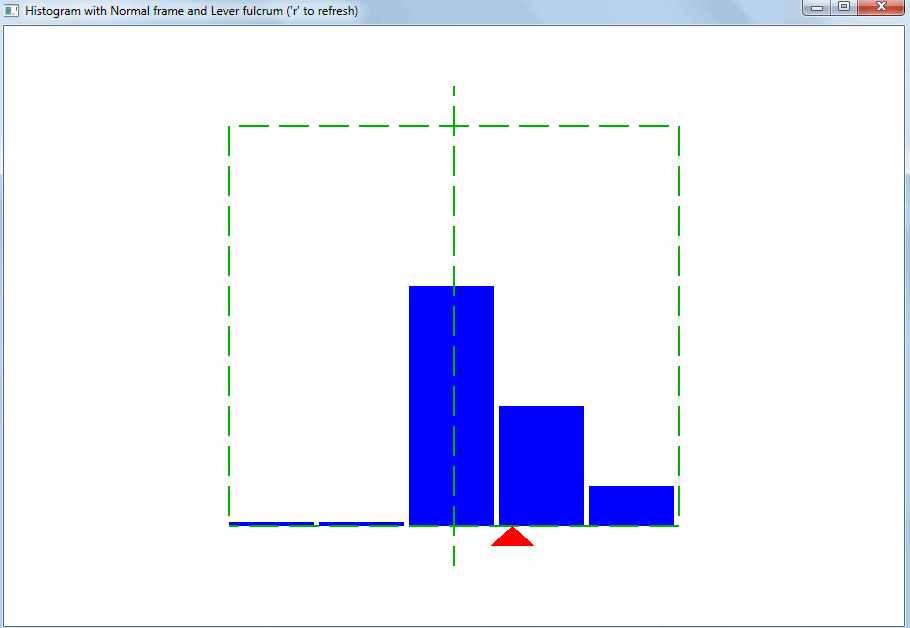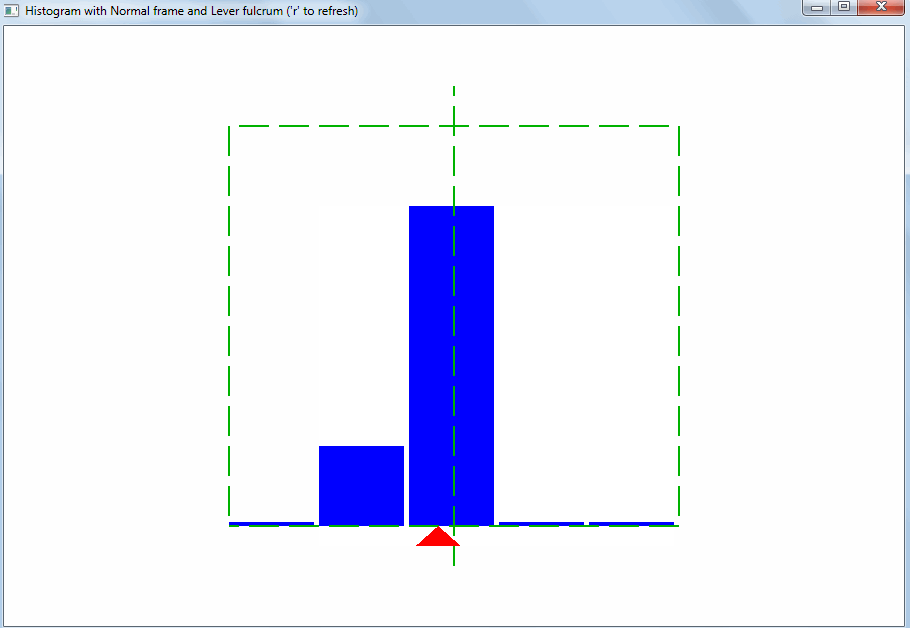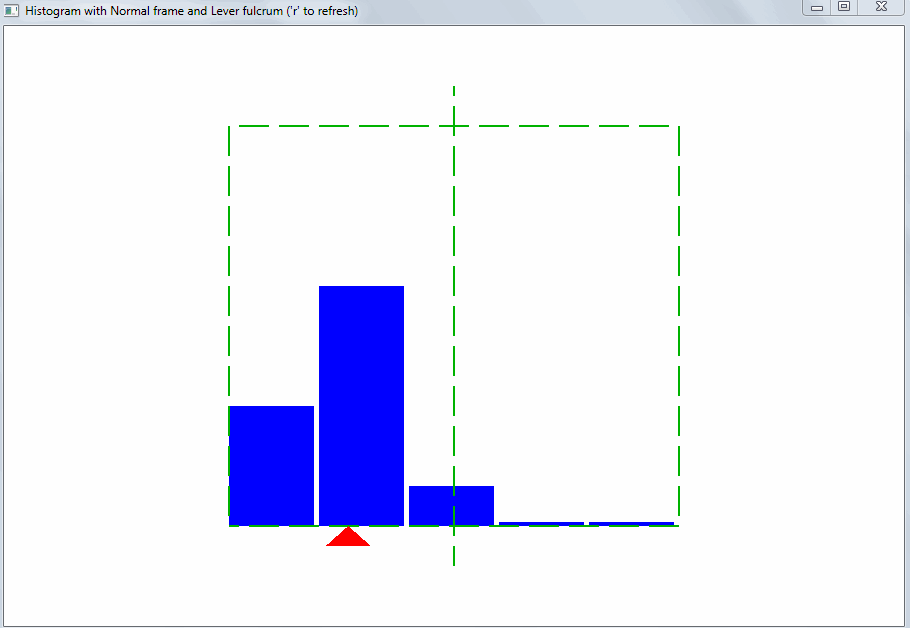
Такого рода отклонение может быть вызвано выбросами. Выбросы – это значения, сильно отличающиеся от остальных. Благодаря правилу рычага, даже небольшое количество выбросов меняет точку равновесия и среднее арифметическое:

Дайте мне точку опоры, и я переверну Землю. Архимед

Выводы

• Среднее арифметическое – интегральная характеристика набора числовых данных (выборки). Применяется как описательная характеристика в совокупности с другими.
• Нормально, что среднее значение не входит в набор данных. Среднее арифметическое не может заменить полное описание полученной выборки.
• Интервал значений гистограммы должен быть подобран таким образом, чтобы ожидаемое среднее арифметическое было посередине. Тогда будет сразу видно отклонение параметров выборки от ожидаемых значений.
• Среднее арифметическое подвержено влиянию выбросов – значений, сильно отличающихся от остальных значений переменной величины.

Ссылки

• Wikipedia: Переменная величина, Моменты в статистике и механике, Момент силы, Математическое ожидание
• Рудольф Арнхейм. Искусство и визуальное восприятие: фрагменты
• Демонстрация гистограммы, ожидаемого среднего и среднего выборки: исходный код для PyOpenGL