Адиабатический компьютер компании D-Wave

Статья завершает цикл публикаций, посвященных критическому анализу квантовой магии: geektimes.ru/post/285378 и geektimes.ru/post/285490. Этот термин почему-то сильно раздражает некоторых адептов новой религии. Но я его не выдумал, а позаимствовал у одного из ее жрецов или, по-меньшей мере, посвященных, пытавшегося издавать журнал и написавшего книгу с таким названием royallib.com/book/doronin_sergey/kvantovaya_magiya.html. Кроме того, название американской компании MagicQ, занимающейся квантовыми системами кодирования, содержит в себе часть заголовка этой статьи до дефиса. Здесь я пытался порассуждать о существующих в реальном мире технологиях, которые принято связывать с квантовой запутанностью в смысле парадокса ЭПР.

Что же такое адиабатический алгоритм?

Известно, что полноценных квантовых компьютеров, оперирующих регистрами с запутанными кубитами, пока не существует. Есть только экспериментальные установки, которые могут что-то делать со считанным числом кубитов. Например говорят, что еще в 2001 IBM сумела разложить число 15 на два простых сомножителя с помощью алгоритма Шора, используя 7 кубитов. Но я не встречал информации о том, что еще какие-то числа поддались этому устройству. Может быть плохо искал, но, как мне представляется, правильней называть его не компьютером, а уникальным, физическим экспериментом.

Прежде уточним, что значит «полноценный квантовый компьютер». Таковым является устройство, реализующее квантовые, параллельные вычисления (см. параграф «Компьютер Бога» в geektimes.ru/post/285490). Если этого нет, то говорить о квантовом компьютере значит морочить людям головы. В том, что касается прогресса и перспектив квантовых технологий этим весьма успешно занимаются журналисты и даже многие ученые. Стоит заметить, что квантовые технологии, вообще говоря, используют уже лет 60 — с момента создания первого мазера, а потом лазера. Сегодня существуют компьютеры, использующие квантовые эффекты.

Примерами такого компьютера являются изделия D-Wave www.3dnews.ru/822671. Известно, что процессоры с регистрами из 128, 512, 1024 и даже 2048 кубитов, которые D-Wave эффектно презентует, не образуют запутанных состояний. Хотя группы по 8 кубитов (кубайты), как утверждается, запутаны внутри себя и есть еще запутанность между отдельными (немногими) кубитами. О черном ящике, которым в буквальном смысле является компьютер D-Wave, известно мало.

Однако известно, что он реализует т.н. адиабатические алгоритмы. В них используется эффект перераспределения энергии между SQUID-ами («кубитами»), в процессе чего регистр релаксирует к состоянию термодинамического равновесия. При этом удается решать весьма узкий класс задач, связанных с целочисленной оптимизацией. Однако, как утверждается, среди них есть задача коммивояжера, которая решается быстрей, чем на любом суперкомпьютере. Это конечно производит впечатление! Очевидно, что речь идет о локальной оптимизации, т.е., о пошаговом улучшении произвольного маршрута в классе тех маршрутов, которые к нему достаточно близки. Тем не менее, с практической точки зрения алгоритмы локальной оптимизации, как правило, работают эффективно.

Что же такое адиабатический алгоритм? Попробую объяснить это на примере, который я придумал сам. Может быть алгоритмы в D-Wave работают совсем не так. Но я не могу себе представить, как иначе употребить процесс перераспределения энергии в системе кубитов. Судите сами, насколько это выглядит правдоподобно. Во всяком случае, как оптимизационный алгоритм должно быть небезинтересным. Технически вполне осуществимо!

В этой связи термин «кубит» не вполне годится, т.к. желательно иметь больше состояний. Есть подходящее слово «кудит». В принципе это — тот же кубит, только имеет не 2, а произвольное число $$ базовых состояний. В случае с кубитом ($$) адиабатически считать тоже можно, но все же предположим, что D-Wave использует кудиты при каком-то $$. И пойдем еще дальше, утверждая, что суперпозиции базовых состояний в данном случае не нужны. Для реализации адиабатического алгоритма достаточно иметь элементы данных, каждый из которых может находиться в одном из $$ энергетических (стационарных) состояний и переходить из одного в другое при взаимодействиях с достаточно близкими к нему элементами. Регистр состоит из $$ таких «кудитов» (так и будем называть их в дальнейшем).

Пусть нужно найти максимум функции $$ при условиях

$$

Коэффициенты $$ и $$ являются целыми, неотрицательными числами. Нужно найти (целочисленное) решение этой оптимизационной задачи. Ниже дан пример того, как она может возникать.

Преобразуем ее, введя новые переменные $$, где $$. Обозначая $$ получаем эквивалентную задачу: найти максимум $$ при условиях

$$

Предполагаем, что уровни энергии являются равноотстоящими на $$. Для запуска алгоритма следует для всех $$ установить кудит номер $$ в состояние с энергией $$, т.е., перебросить его на $$ — й энергетический уровень (начиная с нулевого).

Пусть текущее значение переменной $$ определяется из уравнения $$, где $$ — энергия $$ — го кудита. Тогда все начальные значения $$. В процессе перераспределения энергии между кудитами значения $$ меняются, что эмулирует изменения величин $$.

Теперь предоставим регистру возможность самостоятельно прийти в состояние термодинамического равновесия. В процессе этого кудиты с большей энергией будут передавать ее близким к ним кудитам с меньшей энергией порциями кратными $$. Рассмотрим парное взаимодействие, когда энергия $$ переходит от элемента с энергией $$ к элементу с энергией $$. Тогда новые значения переменных $$ и $$ даются выражениями:

$$

Очевидно, что для таких «транзакций» в большинстве случаев $$, т.е., начальная энергия $$ — го кудита больше, чем $$ — го. Тогда из (2) следует, что $$, т.е., значение целевой функции увеличилось от $$ до $$. При этом $$ является целым, если целым было $$.

Поскольку процесс проходит адиабатически, полная энергия системы не меняется. Следовательно

$$

откуда видно, что новые значения $$ удовлетворяют ограничению (1).

После того, как в системе установится термодинамическое равновесие (это произойдет очень быстро), останется cчитать значения энергии кудитов $$, поделить их на $$ и умножить на $$. Получится решение исходной задачи $$. Заметим, что на каждом шаге алгоритма числа $$ являются целыми, т.е., решается именно задача целочисленной оптимизации. Заметим также, что полученное решение будет локально оптимальным, но, возможно, на практике это нас устроит.

Реальным примером рассмотренной задачи служит следующая (придумана навскидку). Пусть требуется обслужить наибольшее число клиентов в $$ пунктах, в каждый из которых следует пригласить $$ человек. При этом компания располагает денежной суммой $$, которая должна быть потрачена на эту операцию согласно бюджету, а расходы на обслуживание одного клиента в пункте $$ равны $$.

По-видимому, примерно таким образом компьютеры D-Wave решают весьма узкий класс задач оптимизации, которые, однако, представляют практический интерес. Например, умельцы из Google с помощью адиабатических алгоритмов научили D-Wave распознавать на фотографии образ автомобиля. И все же изделия этой компании, хотя и вызывают большой интерес, бесконечно далеки от сколько-нибудь универсального, подлинно квантового компьютера.

Квантовый радар из Поднебесной

Крайне любопытная информация о том, что Китай якобы успешно испытал радар, использующий пары запутанных фотонов, действующий на дистанции до 100 км и способный сделать бесполезной технологию РЛС — невидимости sputniknews.com/military/20161004/1045974842/china-quantum-radar-stealth.html. Этот медиаресурс сильно прокитайский и поменьше пророссийский. Бравый такой агитпроп ))

Как видно, Китай уже вовсю блефует тем, что овладел запутанными технологиям и использует их в спутниковой связи, а также в радиолокации. Идея такого радара вполне очевидна, если поверить в квантовую магию. Один из двух ЭПР — запутанных в поляризациях фотонов пойман в оптический резонатор в виде стоячей волны, а второй отправился на встречу с целью (B2 Spirit). Как только он отразился от поверхности объекта, так сразу, в силу частичного преломления, с вероятностью больше 0.5 приобрел поляризацию перпендикулярно к плоскости падения-отражения. Это означает, что состояние поляризации одного из двух фотонов пары изменилось. Согласно ЭПР — парадигме (она же квантовая магия) поляризация второго фотона — того, что скучает в резонаторе, также изменилась. Поскольку это произошло не с одной фотонной парой, а со многими, изменение поляризации поля в резонаторе можно детектировать. Попался, Spirit? Сейчас мы из тебя дух-то вышибем по имя светлых идей Мао! ))

Важно обратить внимание на то, что обнаружение цели происходит не тогда, когда отраженный фотон вернулся к передачику, а сразу, как только он отразился от объекта. Легко понять, что это грубо противоречит СТО. В самом деле, пусть лазерный луч с фотонами, входящими в запутанные пары, светит в фиксированном направлении. Лишь только злоcчастный B2 наткнулся на луч, в то же мгновение воины НОАК определили азимут и угол места цели. Они-то знали эти углы заранее, когда фиксировали направление луча, но американец сообщил о своей встрече с лучом раньше, чем его можно было бы увидеть в этом месте! Если это не превышение предельно допустимой скорости передачи сигналов $$ м/сек, то что?

Адептов и любителей квантовой магии данный факт совершенно не смущает. Давно привычно объяснять странные эффекты тем, что мол законы физики писаны в классическом пространстве, а квантовая физика далеко проникает за его пределы, где действуют другие правила (что-то вроде того, как прокалывание искривленного пространства черной дырой драматически сокращает расстояния между звездами). Я не берусь точно воспроизвести философские объяснения, основанные на вере в квантовые чудеса. Но исходя из той физики, которая подтверждена экспериментами, такого произойти не может.

Стало быть, радар на запутанных фотонах фикция? И да и нет. В том виде, как я в шутливой форме описал — однозначно ДА. Но можно домыслить механизм работы этого радара, который имеет чисто квантовую природу. Итак, никаких запутанных пар не возникает. Вместо этого каждый фотон делится на две моды, одна из которых остается в резонаторе, а другая отправляется на встречу с целью (см. по этому поводу цитату из Дирака в п. «Опыт Аспэ» geektimes.ru/post/285378). После возвращения отраженной моды и поглощения радаром всего фотона поле в резонаторе ослабевает. При большом числе фотонов это можно детектировать.

Оценивая эти рассуждения важно понимать, что фотон не имеет представления Шредингера. А это означает, что не имеет местоположения в пространстве. Фотон присутствует везде, где есть поле, частью которого он является, грубо говоря. По этому поводу полезно почитать введение в книгу Дирака «Принципы квантовой механики», где он рассуждает о фотонах. Это займет лишь несколько минут, но поможет избавиться от навязчивого образа фотона — точечной частицы, лежащего в основе ложной интерпретации опытов Аспэ.

Таким образом, по-видимому, имеет место обычная локация, но фотонами. Понятно, что лишь малая их часть возвращается к радару. Однако отраженная мода фотона будет рассеянной волной, поэтому вероятность ее возвращения на место излучения не так уж и мала. Все эти эвристические рассуждения, конечно, могут быть ошибочными. Однако, мое объяснение основано на КМ и не привлекает такие мистические сущности, как запутанные состояния бесконечно удаленных частиц.

Ясно одно: китайцы создали радар на фотонах, который позволяет обнаружить самолет за пределами прямой видимости. Это — успех технологий волновой оптики и фотоники. Возможно, что такой радар повысит уязвимость самолетов-невидимок. Но вряд ли к этому причастна квантовая магия, хотя сами китайцы свято веруют в обратное.



Рисунок из статьи на эту тему wonderfulengineering.com/the-chinese-have-allegedly-developed-a-quantum-radar-that-can-detect-american-stealth-planes, в котором я не смог разобраться, не зная аббревиатур. Это явно не имеет отношения к запутанным фотонам. Похоже на обычную локацию фотонами.



На этом рисунке из той же статьи, насколько можно судить, принцип работы доплеровского радара.

Криптография и cпонтанное параметрическое рассеяние

Системы квантовой криптографии применяются десяток лет, если не больше. Их постоянно смешивают с квантовой магией, но, по-видимому, она не имеет никакого отношения к таким системам. В качестве примера рассмотрим алгоритм генерации секретного ключа BB84, описанный здесь ru.wikipedia.org/wiki/Квантовая_криптография.

Механизм защиты основан на том, что если злоумышленник Ева перехватит бит, переносимый поляризованным фотоном, то тем самым она переведет его в состояние поляризации, которое может отличаться от заданного Алисой. В процессе сверки переданных битов между Алисой и Бобом это изменение поляризации будет обнаружено. Используется квантовый эффект — переход фотона в собственное состояние измеренной поляризации, но ЭПР — запутанность здесь не при чем.

Таким образом, реально существующие системы квантовой криптографии играют роль важного аргумента в пользу квантовой магии, но на деле таковым не являются. Что касается теоретических результатов в этой области, основанных на ЭПР — запутанности, то их физическая осуществимость связана с теми же фундаментальными проблемами, что и телепортация и квантовые вычисления geektimes.ru/post/285490.

В статье wonderfulengineering.com/the-chinese-have-allegedly-developed-a-quantum-radar-that-can-detect-american-stealth-planes приводится рисунок, изображающий cпонтанное параметрическое рассеяние фотона в качестве гипотетического источника запутанных пар для квантового радара. Считается, что в ходе этого процесса фотон, проходя через нелинейный кристалл, спонтанно распадается на два запутанных в поляризациях фотона. Это — известный с конца 60-х, довольно слабый эффект. Рождающуюся в результате пару называют бифотоном, теоретически она получается запутанной.



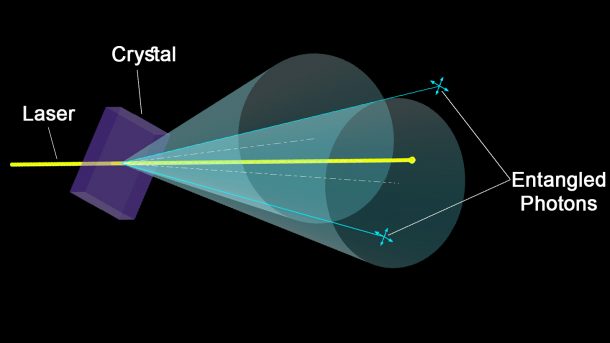
Спонтанное параметрическое рассеяние (spontaneous down conversion)

Но в самом ли деле здесь возникают два фотона, как показано на рисунке, или правильней было бы говорить о двух модах одного фотона на выходе из кристалла? То есть о чем-то вроде двойного лучепреломления? В некоторых статьях на эту тему авторы осторожно пишут, что распад фотона на два не стоит воспринимать слишком буквально. Судя по тому, что данный эффект регистрируется через интерференцию «фотонов пары», можно уверенно утверждать, что пары здесь не возникает. Дело в том, что, в соответствии с КМ, фотон может интерферировать только с самим собой! В своей фундаментальной книге П.А.М. Дирак прямо пишет, что два разных фотона никогда не интерферируют (см. введение). На теорию спонтанного параметрического рассеяния данное обстоятельство, предположительно, существенно не повлияет. Однако, оно выбьет важную подпорку из-под мифа о запутанных фотонах, остающихся таковыми после разлета на расстояния в десятки и сотни км (ЭПР — запутанность). Разумеется, данный вопрос нуждается в точном исследовании.

Итог трех публикаций, выражающий мою личную точку зрения. Квантовая магия не имеет под собой теоретических оснований, является продуктом произвольных спекуляций с формализмом КМ и, в действительности, не подтверждается экспериментами. Основополагающие опыты Аспэ были ошибочно интерпретированы на основе классического представления о том, что излученные в одном каскаде фотоны имеют собственные значения импульсов и угловых моментов одновременно (что невозможно в силу КМ и КЭД). ЭПР — парадигма не воплощается в реальных, квантовых технологиях вопреки тому, что принято думать под давлением журналистов и не вполне добросовестных ученых. Научному сообществу остро не хватает критической оценки данной парадигмы, которая фактически стала догмой.

P.S. Мои статьи ни в какой мере не подвергают сомнению собственно квантовую механику. Обратные утверждения адептов квантовой магии являются свидетельством той недобросовестности, о которой сказано выше.