31.01.2017 20:23
SpaceOdyssey 110 17500 Источник
image

Феномен квантовой запутанности (entanglement), когда разделенные в пространстве частицы мистическим образом взаимодействуют друг с другом, нахально нарушая запрет на передачу взаимодействий со сверхсветовой скоростью, давно считается частью науки и у научного сообщества не вызывает никаких сомнений. Вполне серьезно изучаются перспективы создания на этой основе квантовых компьютеров. Считается, что их элементы данных — кубиты будут изменять и передавать свое информационное состояние посредством механизма квантовой запутанности. Такая прагматичная организация, как DARPA щедро финансирует эту чудесную науку. А между тем имеет серьезные основания точка зрения, согласно которой квантовая запутанность в смысле парадокса ЭПР — это миф, который прижился в поверхностном слое понимания квантовой механики.

Парадокс ЭПР


Эйнштейн предпринял атаку на квантовую механику со знаменем в руках, на котором было написано «Бог не играет в кости». В знаменитой статье [0], опубликованной в 1935-м, появился т.н. парадокс ЭПР (Эйнштейна, Подольского, Розена). Из этого парадокса, который на самом деле является софизмом, родился миф о квантовой запутанности.

Основная идея ЭПР, согласно статье его авторов, выглядит следующим образом. Пусть имеется пара квантовых объектов 1 и 2, образующих единую систему с волновой функцией $\Psi(x_1, x_2)$, где наборы переменных $x_1$ и $x_2$ используются для описания поведения подсистем 1 и 2 в отдельности. Если задан полный набор $u_1(x_1), u_2(x_1), \ldots, u_n(x_1), \ldots$ собственных волновых функций для некоторых наблюдаемых системы 1, то функция $\Psi(x_1, x_2) $разлагается в ряд Фурье:

$\Psi(x_1, x_2)=\sum_{n=1}^{\infty}\varphi_n(x_2)u_n(x_1)$

Теперь предположим, что подсистемы удаляются друг от друга и через некоторое время расстояние между ними стало настолько большим, что взаимное влияние невозможно. Если затем измерить значения (коммутирующих) наблюдаемых системы 1, то, в силу принципов квантовой механики, она скачком перейдет в некоторое собственное состояние $u_k(x_1)$. В контексте запутанной парадигмы это событие имеет драматическое название «коллапс волновой функции». Следовательно, рассуждают далее авторы ЭПР, вся система в целом скачком переходит в состояние c волновой функцией $\varphi_k(x_2)u_k(x_1)$. Это означает, что подсистема 2 внезапно оказалась в состоянии $\varphi_k(x_2)$, хотя никакого воздействия подсистемы 1 и измерительных приборов на нее не было.

Перед нами главный эффект, с которым связано представление о нелокальности квантовой механики, а именно — непонятное и необъяснимое, мгновенное взаимодействие удаленных квантовых объектов 1 и 2. Оно заключается в том, что при измерении некоторых физических величин, связанных с системой 1, автоматически и сразу меняется состояние системы 2.

В приведенных рассуждениях есть сразу две ошибки. Первая заключается в том, что волновая функция $\varphi_k(x_2)u_k(x_1)$, вообще говоря, не отвечает собственному состоянию объединенной системы. Поэтому последняя не обязана переходить в $\varphi_k(x_2)u_k(x_1)$ скачком при измерении, связанном только с системой 1. И все же возникает вопрос: в каком состоянии окажется подсистема 2 после измерения 1? Ответ прост и очевиден — ее состояние не изменится. В самом деле, поскольку в рассматриваемой ситуации объекты 1 и 2 независимы, то

$\Psi(x_1,x_2)=\Psi_1(x_1)\Psi_2(x_2)=\Psi_2(x_2)\sum_{n=1}^{\infty}c_nu_n(x_1)=\sum_{n=1}^{\infty}c_nu_n(x_1)\Psi_2(x_2)$

где $\Psi_j(x_j)$ — волновая функция системы $j=1, 2$, рассматриваемой в отдельности. Следовательно, как только подсистема 1 оказалась в собственном состоянии $u_k(x_1)$, подсистема 2 автоматически оказывается в… своем исходном состоянии $\Psi_2(x_2)$. Что и следовало ожидать!

Вторая ошибка заключается в том, что пара не взаимодействующих объектов 1 и 2, формально объединенных в единую систему, на самом деле не испытывает возмущения при измерении, которое связано лишь с подсистемой 1. Такое «возмущение» не способно вызвать скачок объединенной системы в одно из собственных состояний (полного набора коммутирующих наблюдаемых, полученного объединением наборов 1 и 2). Для этого нужно было бы возмутить всю систему в целом, т.е., реально подействовать также и на объект 2.

Таким образом, псевдопарадокс ЭПР лишь вынуждает нас уточнить понятие возмущения. Но вместо этого ему придают абсолютный и формальный смысл, как если бы взмах крыла бабочки считался возмущением Вселенной,… хотя с философской точки зрения так оно и есть. Выше дан точный ответ на вопрос, что именно происходит с подсистемой 2 после измерения 1. По существу ничего!

Из своего псевдопарадокса авторы ЭПР сделали далеко идущие выводы о неполноте квантовой механики, т.е. о том, что эта теория нуждается в дополнительных параметрах для описания квантовых систем. Параметрах, которые исключают всякую неопределенность и делают их поведение детерминированным в классическом духе. С точки зрения Эйнштейна наука пока просто не знает этих скрытых параметров и законов их поведения, поэтому ограничивается вероятностным характером квантовых прогнозов.

В популярных объяснениях эффекта квантовой запутанности пары частиц, после вольного изложения ЭПР всегда ссылаются на законы сохранения. Рассмотрим случай пары электронов. Рассуждать о сохранении импульса нет смысла, хотя часто приводится пример пары «запутанных» электронов с импульсами $\pm\vec p$. Поскольку оператор импульса имеет непрерывный спектр, его собственные состояния практически не могут быть реализованы. Поэтому на квантовом уровне бессмысленно рассматривать пару электронов с импульсами $\pm\vec p$. Таким образом, отбросим импульс в сторону и рассмотрим случай «запутанной» пары электронов с нулевой суммарной проекцией спина на ось Z (синглет).

Сохранение проекции спина означает, что для оператора $m_z$ проекции спина на ось Z имеет место $ [m_z, H]=0$, где $H$ — оператор энергии данной системы. В частности это означает, что если система первоначально находится в собственном состоянии оператора $m_z$, то в дальнейшем, при отсутствии внешних возмущений она будет при каждом $t$ находиться в собственном состоянии наблюдаемой $m_z$, хотя вектор состояния может изменяться во времени.

Для единственного электрона оператор $m_z$ имеет два собственных вектора, обозначим их $|1\rangle$ и $2\rangle$, так что

$m_z(|1\rangle)=\frac{1}{2}\frac{h}{2\pi} |1\rangle \qquad m_z(|2\rangle)=-\frac{1}{2}\frac{h}{2\pi} |2\rangle$

Предположим, что пара электронов первоначально находится в состоянии $c\cdot(|1,2\rangle-|2,1\rangle)$, где $c$ — любое комплексное число. Здесь вектор $|a,b\rangle$ отвечает такому состоянию пары, что первый электрон находится в состоянии $|a\rangle$, а второй в состоянии $|b\rangle$. Состояние $c\cdot(|1,2\rangle-|2,1\rangle)$ является собственным для спина $M_z$ системы из двух электронов, поэтому при измерении система останется в этом состоянии и будет получено нулевое значение $M_z'=0$ для спина пары.

В процессе разбегания электронов в разные стороны спиновое состояние синглета не изменится, если система остается изолированной вплоть до момента первого измерения. Это означает, что при каждом $t$ пара электронов находится в состоянии $c(t)\cdot(|1,2\rangle-|2,1\rangle)$, которое является собственным для оператора $M_z$ и отвечает собственному значению $M_z'=0$. Согласно популярным рассуждениям о паре запутанных электронов, при измерении спина одной из частиц произойдет скачок системы в собственное состояние оператора $M_z$. Но согласно квантовой механике, поскольку система уже находится в собственном состоянии (полного набора коммутирующих наблюдаемых, включающего $M_z$, она останется в нем после измерения. Соответственно, изменится разве лишь числовой множитель перед вектором $|1,2\rangle-|2,1\rangle$.

Таким образом, перехода измеряемого электрона в состояние $|1\rangle$, а второго в состояние $|2\rangle$ не произойдет. Получено противоречие с тем фактом, что измеряемый электрон все-таки перейдет в собственное состояние своего оператора $m_z$. Отсюда следует, что при измерении спина одного из электронов совместное состояние синглета будет разрушено. При этом состояние второго электрона останется неизменным, т.е., неопределенным с точки зрения спина, а именно $|1\rangle+|2\rangle$.

В рамках запутанной парадигмы также рассматривают пару фотонов в одинаковых состояниях поляризации, так что общее состояние пары можно задать вектором $c(|1,1\rangle+|2,2\rangle)$, где $|1\rangle$ и $|2\rangle$ задают состояния поляризации в перпендикулярных направлениях. Если при измерении одного из фотонов он перейдет в собственное состояние $|1\rangle$, то якобы это повлечет переход пары в состояние $|1,1\rangle$, т.е., мгновенный скачок второго фотона в такое же состояние поляризации $|1 \rangle$. Однако, аналогично примеру с синглетом электронов можно утверждать, что пара фотонов останется в собственном состоянии $c(|1,1\rangle+|2,2\rangle)$. Это противоречие означает, что измерение одного из двух фотонов разрушает систему, после чего второй фотон остается в исходном состоянии $|1\rangle+|2\rangle$. Запутанности в смысле ЭПР и здесь не возникает.

image

Неравенства Белла


В 1964 Джон Стюарт Белл написал интересную статью [1], в которой подверг критическому анализу гипотезу о скрытых параметрах. Эти, на удивление простые рассуждения Белла оказали большое влияние на развитие квантовой физики с конца XX века по настоящее время.

По ходу своих рассуждений Белл вывел неравенство $1+P(\vec b, \vec c)\geq |P(\vec a, \vec b)-P(\vec a, \vec c) |$, где $\vec a, \vec b, \vec c$ — это единичные векторы различных направлений в пространстве, на которые проектируются спины двух разбегающихся в разные стороны частиц (электронов). Изначально частицы имеют нулевой суммарный спин, т.е. образуют синглет. При этом $P(\vec a, \vec b)$ обозначает ненормированный коэффициент корреляции пары случайных величин $\vec\sigma_1\cdot \vec a$ и $\vec\sigma_2\cdot \vec b$, являющихся проекциями спиновых переменных $\vec\sigma_1$ и $\vec\sigma_2$ частиц 1 и 2 на направления векторов $\vec a$ и $\vec b$ соответственно. Другими словами $P(\vec a, \vec b)$ — это среднее значение произведения чисел $\vec\sigma_1\cdot \vec a$ и $\vec\sigma_2\cdot \vec b$. Которые, заметим, принимают значения $\pm 1$. Данное неравенство имеет место при условии, что верна гипотеза Эйнштейна о скрытых параметрах $\lambda$ квантовой системы. И оно может быть проверено статистически. В дальнейшем были аналогично получены другие неравенства, которые применимы не только к синглетной паре электронов, и все они называются неравенствами Белла. Например такое:

$|P(\vec a, \vec b)+P(\vec a, \vec b')+P(\vec a', \vec b)- P(\vec a', \vec b')|\leq 2$

Оно также справедливо лишь в том случае, если есть скрытые параметры $\lambda$ квантовой системы, определяющие ее поведение. При этом, поскольку законы поведения этих параметров неизвестны, они считаются случайными величинами.

Для иллюстрации последнего утверждения, рассмотрим опыт с бросанием монеты. Понятно, что полет брошенной монеты определяется многими величинами, которые описывают ее форму, распределение массы, детальные условия броска, форму поверхности падения и другие факторы, от которых зависит ответ на вопрос: «орел или решка». При полном учете всех этих «скрытых параметров», которые Белл обозначает символом $\lambda$, можно было бы дать 100% надежный прогноз того, как именно упадет монета. Однако такой учет слишком сложен, и в этом нет большой необходимости, поэтому довольствуются вероятностным прогнозом того, как упадет монета. Соответственно, скрытые параметры следует считать случайными величинами. Вопрос: существуют ли аналогично скрытые параметры у любой квантовой системы, или же таких параметров нет, а стохастическое поведение субатомных объектов заложено в природе вещей?

В экспериментах с т.н. запутанными частицами, чаще всего фотонами, искомым результатом всегда является нарушение неравенства Белла. Такие нарушения в самом деле наблюдаются с конца 70-х годов прошлого века, и сегодня принято толковать их, как доказательства возникновения запутанных квантовых состояний. При этом значительные усилия экспериментаторов направлены на то, чтобы разнести на возможно большие расстояния приборы, которые регистрируют спины частиц или направления поляризации фотонов, чтобы исключить взаимное влияние объектов и приборов измерения. Сделав тем самым максимально убедительным эффект мгновенной передачи взаимодействий, положенный в основу фантазий о квантовой телепортации.

Однако в действительности, нарушение неравенств Белла означает одно из двух.

a) У квантовых систем нет скрытых параметров. Это полностью соответствует квантовой механике и не связано с запутанностью.

b) Скрытые параметры есть и тогда измерения одной из подсистем могут влиять на другую. Поэтому квантовая запутанность имеет место быть.

Соответственно нет оснований утверждать, что нарушения неравенств Белла экспериментально доказывают феномен ЭПР — запутанности. Разумно предположить, что они влекут за собой a), т.е., что квантовая механика не нуждается в скрытых параметрах и апгрейде в духе Бома. Однако, принято считать эти нарушения свидетельствами ЭПР — запутанности фотонных пар.

Данная парадигма сформировалась под влиянием работ Аспэ и других ученых, поставивших аналогичные эксперименты. Помимо несомненных нарушений неравенств Белла, в них якобы наблюдались корреляции между направлениями поляризации взаимно удаленных фотонов. Будь это так, для опытной проверки ЭПР — запутанности в неравенствах Белла не было бы необходимости. Стоит заметить, что сам Аспэ, судя по статье [1], считал свидетельством запутанности только корреляции. Но в действительности наблюдалась «корреляция» каждого фотона, попавшего в фотоумножитель, с самим собой. Точнее: он достигал двух фотоумножителей почти одновременно (см. ниже).

Опыт Аспэ


Опыт Алана Аспэ (Aspect) — блестящего экспериментатора и классика квантовой магии, внес основной вклад в трансформацию ЭПР — мифа в догму. Результаты опытов Аспэ и других были интерпретированы на основе представления о фотонах, как точечных частицах (с обычными оговорками о корпускулярно-волновом дуализме). Оно является ошибочным, т.к. у фотона нет представления Шредингера [2]. Говоря простым языком, для этих частиц понятие пространственных координат лишено смысла. Поэтому нельзя говорить о том, что в определенный момент времени фотон находится в определенном месте. Он может быть локализован в состоянии малого волнового пакета, но в этом случае поляризация теряет смысл.

В связи с этим уместно процитировать Дирака (P.A.M. Dirac, стр. 25 [2]).

"… Пусть мы имеем пучок света, состоящий из большого числа фотонов, который расщепляется на две компоненты одинаковой интенсивности. Сделав предположение о том, что интенсивность пучка связана с вероятным числом фотонов, мы получили бы, что в каждую из компонент попала бы половина от общего числа фотонов. Если далее эти две компоненты будут интерферировать, то мы должны потребовать, чтобы фотон из одной компоненты мог интерферировать с фотоном в другой компоненте. Иногда эти два фотона уничтожались бы, иногда же они превращались бы в четыре фотона. Это противоречило бы закону сохранения энергии. Новая теория, которая связывает волновую функцию с вероятностями для одного фотона, преодолевает эту трудность, считая, что каждый фотон входит отчасти в каждую из двух компонент. Тогда каждый фотон интерферирует лишь с самим собой. Интерференции между двумя разными фотонами никогда не происходит."

Аналогичная мысль звучит в цитате из Гейзенберга, которая касается парадокса ЭПР и имеет отношение к интерпретации опытов Аспэ (W. Heisenberg, стр. 34 [3]).

"В связи с этими рассуждениями здесь должно быть указано на мысленный эксперимент, предложенный Эйнштейном. Вообразим один световой квант, который представлен посредством волнового пакета, построенного из максвеллевских волн и которому, таким образом, приписана известная область пространства и, в смысле соотношений неопределенности, также определенная область частот. Посредством отражения от полупрозрачной пластинки мы можем очевидно легко разложить этот волновой пакет на две части: отраженную и прошедшую. Тогда существует определенная вероятность найти световой квант или в одной, или в другой части волнового пакета. Через достаточно долгое время обе части будут сколько угодно далеко удалены друг от друга. Если теперь посредством опыта будет установлено, что световой квант находится, положим, в отраженной части волнового пакета, то это одновременно даст, что вероятность нахождения светового кванта в другой части равна нулю. Опыт на месте отраженной половины пакета производит тем самым некоторое действие (сведение волнового пакета!) на сколь угодно удаленном расстоянии, где находится другая половина, и легко видеть, что это действие распространяется со сверхсветовой скоростью."

Таким образом, попытки обнаружить ЭПР — запутанные пары фотонов с помощью интерферометра лишены смысла. Допустим, мы разделили световой луч полупрозрачным зеркалом, после чего пропустили один пучок через поляризатор. Согласно парадигме ЭПР, возникают запутанные пары одинаково поляризованных фотонов из двух пучков. Это может быть проверено через интерференцию, но так как интерферировать каждый фотон будет с самим собой, совпадение измеренных в разных местах поляризаций не может быть истолковано, как ЭПР — запутанность.

Неявно предполагаемая возможность поляризации точечного фотона легла в основу ложной интерпретации опытов Аспэ. Начнем с краткого описания этих экспериментов (подробности в статье [1]).

Использовались флуоресцентные источники каскадного излучения, где атомы испускают пары квантов с интервалом $\tau\approx 5$ нс. В первых опытах один из фотонов пары имел длину волны 551.3 нм (зеленый свет), а другой 422.7 нм (фиолетовый). Исходя из законов сохранения импульса и момента импульса считается, что в каждом каскаде фотоны разлетаются в разные стороны, имея одинаковые направления круговой поляризации — левое или правое с вероятностями 0.5, что равносильно пребыванию в суперпозиции двух состояний линейной поляризации в направлениях осей X и Y. Как полагают Аспэ и его последователи, эта пара квантов света рождается в запутанном, поляризационном состоянии:

$|\Psi\rangle=\frac{1}{\sqrt{2}}\left(|R_1\rangle\otimes|R_2\rangle+|L_1\rangle\otimes|L_2\rangle\right)=\frac{1}{\sqrt{2}}\left(|x\rangle\otimes|x\rangle+|y\rangle\otimes|y\rangle\right)$


$|R_1\rangle=|L_2\rangle=\frac{1}{\sqrt{2}}(|x\rangle+i|y\rangle),\qquad|L_1\rangle=|R_2\rangle=\frac{1}{\sqrt{2}}(|x\rangle-i|y\rangle)$


Состояния $|x\rangle$, $|y\rangle$ отвечают направлениям поляризации вдоль осей координат, состояния $|R_j\rangle$, $|L_j\rangle$ — двум направлениям круговой поляризации фотона номер $j=1,2$.

ЭПР — запутанность означает, что если один из фотонов будет обнаружен поляризованным вдоль оси X (для чего достаточно пропустить его через поляризатор с X — ориентацией), то второй автоматически, в то же мгновение окажется в том же состоянии (что можно обнаружить с помощью второго поляризатора). То же самое в отношении оси Y. В этом случае говорят о корреляции между направлениями поляризации фотонов запутанной пары, которую можно измерить.

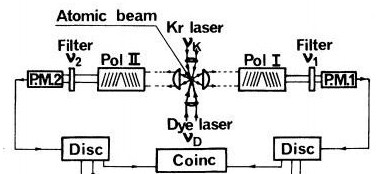
image

Схема опыта Аспэ

На схеме пара лазеров возбуждает флуоресцентный источник каскадного излучения, который, по мысли Аспэ, излучает пары запутанных фотонов. Каждый из них проходит через свой поляризатор (Pol I и Pol II), после чего, пройдя через частотный фильтр, попадает в фотоумножитель (PM I и PM II). Последний, по существу, является детектором одиночных фотонов и работает по принципу электронной лавины, которую инициирует фотоэффект. Схема управления фотоумножителями организована так, что каждая пара квантов детектируется во временном окне около 20 нс. Попадание в него случайной пары фотонов от двух разных атомов маловероятно. Таким образом, схема почти наверняка зафиксирует только пару, излученную в одном каскаде. Происходит это в среднем 100 раз в секунду. Напомним, что каждая такая пара считается ЭПР — запутанной.

Если теперь за некоторый период времени подсчитать числа пар для случаев, когда один из поляризаторов («левый» или «правый») удален, то можно вычислить коэффициент корреляции между событиями поляризованности левого фотона в заданном направлении $\vec a$, а правого в направлении $\vec b$. Такие измерения позволяют проверить неравенства Белла, а также выявляют корреляцию между поляризациями фотонов каждой пары (для различных направлений $\vec a$ и $\vec b$). Именно это было сделано группой Аспэ.

Однако, в опыте Аспэ мог иметь место подсчет одиночных фотонов, которые достигали двух фотоумножителей в виде волн со сферическими фронтами (волновыми поверхностями). Согласно квантовой электродинамике [4], поле фотона с заданным моментом импульса распространяется именно в виде такой волны. Можно доказать, что эта волна приходит к каждому из двух поляризаторов в одинаковых фазах, хотя и в разные моменты времени в силу различной удаленности от излучателя. При этом угол между вектором напряженности поля $\mathbf E$ и осью каждого поляризатора один и тот же для любой волновой поверхности. Поэтому волна одного фотона взаимодействует с двумя поляризаторами одинаково. Это и создает иллюзию пары частиц, запутанных в поляризациях.

На сказанное можно возразить, что счетчик фотонов срабатывает дважды в среднем через $\approx 5$ нс, как и должно быть при излучении каскадов. Однако, время срабатывания фотоумножителя элементарно оценивается $\sim 10$ нс. В течение этого времени может быть зафиксирован только один фотон. В действительности он является волновым пакетом, центрированным на сфере $|{\mathbf r}|=ct$. Если размер пакета $\Delta r\sim 1$ м, что отвечает допплеровскому уширению спектральной линии $ \sim 10^{-3} \buildrel _\circ \over {\mathrm{A}}$, то время прохождения через фотоумножитель имеет порядок интервала между фотонами одного каскада. В условиях опытов Аспэ такое уширение было возможно. Таким образом, до срабатывания пары фотоумножителей на первом фотоне второй не мог быть детектирован, а к моменту, когда оба устройства готовы принять второй фотон, его пакет уже прошел. По-видимому, в большинстве случаев пара фотоумножителей фиксировала только один из двух фотонов каждого каскада.

Заметим также, что в рассматриваемом состоянии направление движения фотона не определено. Это связано с тем, что импульс и его момент не коммутируют. Следовательно, аналогии с классической механикой, которые используются в качестве причины запутанного состояния пары фотонов, в данном случае неуместны. Кроме того, излучение фотона сопровождается возмущением. После него атом окажется не в состоянии с нулевым моментом, а в суперпозиции собственных состояний момента. Таким образом, законы сохранения не влекут состояние пары фотонов одного каскада вида

$|\Psi\rangle=\frac{1}{\sqrt{2}}\left(|R_1\rangle\otimes|R_2\rangle+|L_1\rangle\otimes|L_2\rangle\right)=\frac{1}{\sqrt{2}}\left(|x\rangle\otimes|x\rangle+|y\rangle\otimes|y\rangle\right)$

За время излучения расстояние между фотонами пары составит $\sim 1$ м. Идея о том, что такая пара рождается запутанной, противоречит здравому смыслу. Впрочем, последнее относится ко всей квантовой магии.

Таким образом, результаты опытов Аспэ имеют интерпретацию, которая не связана с ЭПР — запутанностью. Необходимы более точные оценки, но уже есть основания предполагать, что в этих экспериментах совместные, ЭПР — запутанные состояния не наблюдались. По-видимому, подобным образом можно объяснить все опыты с т.н. запутанными фотонами.

Представления о запутанных состояниях взаимно удаленных частиц, восходящие к парадоксу ЭПР, широко популяризованы и уже считаются частью квантовой механики. Одной из целей данной статьи было показать, что фундамента под этим нет. Мыльный пузырь на иллюстрации символизирует волновой фронт фотона с заданным угловым моментом, а также теорию квантовых компьютеров, основанную на ЭПР — запутанности.

Ссылки
0. Einstein A., Podolsky B., Rosen N., Can Quantum-Mechanical Description of Physical Reality Be Considered Complete,

1. A. Aspect. Bell's theorem: the naive view of an experimentalist, in Quantum [Un]speakables — From Bell to Quantum information, 2002, R. A. Bertlmann and A. Zeilinger, Springer.

2. П.А.М. Дирак. Принципы квантовой механики, 1960, Москва: Физматгиз (перевод английского издания P.A.M. Dirac. The principles of quantum mechanics, 1958, Oxford: Clarendon press), 1932).

3. В. Гейзенберг. Физические принципы квантовой теории, Москва: ГТТИ (перевод немецкого издания W. Heisenberg: Die Physikalischen Prinzipien der Quantentheorie, 1930, Leipzig).

4. В.Б. Берестецкий, Е.М. Лифшиц, Л.П. Питаевский. Квантовая электродинамика, Москва: Наука, 1989.
Поделиться с друзьями
-->

Комментарии (110)


  1. SpaceOdyssey
    31.01.2017 23:34
    #9856474
    +2

    Данная статья в доступной форме представляет основной вывод многолетних размышлений о парадигме квантовой запутанности в том виде, как ее принято понимать в смысле псевдопарадокса ЭПР. Этот вывод является конечно спорным, и многим он резко не понравится. Особенно тем, кто увлечен квантовым компьютингом. Хотя именно эта тема в статье не затронута. Я не смогу активно и оперативно отвечать на все вопросы, но постараюсь не оставлять без ответа содержательные ones, хотя это может происходить с задержками. Заранее за них извиняюсь ))


    1. Dr-Good
      01.02.2017 00:28
      #9856570
      +4

      Насчет доступной формы я бы поспорил, моим гуманитарным мозгам было тяжеловато:) Было бы здорово, если бы вы добавили к статье суть «разоблачения» что называется на пальцах, для людей неподготовленных.


      1. saboteur_kiev
        01.02.2017 01:38
        #9856670
        -7

        Как я понял из статьи, построить что-либо на технологии квантовой зависимости нельзя, потому что квантовая теория скорее всего миф.


        1. SpaceOdyssey
          01.02.2017 07:53
          #9856942
          +5

          Нет конечно! Квантовая механика — это никакой не миф. Проблема скорее в том, что ее плохо понимают многие современные ученые. Немало времени требует осмысление, а хочется быстрей писать статьи. Мифом является квантовая магия. То есть набор идей, врашающихся вокруг ЭПР — запутанности. Вроде бы объяснил это в статье. Но повторю.


          ЭПР — запутанность, которую называют квантовой запутанностью, это идея о том, что две взаимно удаленные на физически бесконечное расстояние квантовые системы могут, тем не менее, неким таинственным образом влиять на состояния друг друга. Это — вовсе не квантовая механика. как принято думать, а формальные спекуляции, основанные на квантовой механике. Вы бы статью все же прочитали вдумчиво для начала, иначе не выйдет обсуждения ))


          1. GreatRash
            01.02.2017 09:55
            #9857236
            +15

            Жили-были 14 непонятных объяснений квантовой механики…
            — Они все непонятные! Смотрите, сейчас я объясню вам на пальцах!
            Жили-были 15 непонятных объяснений квантовой механики…


          1. geisha
            01.02.2017 17:29
            #9858730
            +1

            Проблема скорее в том, что ее плохо понимают многие современные ученые.
            Точно. Но насчет «многие» — тут я бы не был так уверен.
            это идея о том, что две взаимно удаленные на физически бесконечное расстояние квантовые системы могут, тем не менее, неким таинственным образом влиять на состояния друг друга.
            Есть некий эффект. Он заведомо находится за гранью нашего повседневного опыта. Его можно либо хорошо и годно описать формулами либо нехорошо и негодно — словами. С этой точки зрения мне совершенно все равно, будет у вас написано «таинственно», «магически» или «метафизически».

            Что меня лично раздражает — так это то, что постоянно разоблачают именно квантовую физику / релятивизм. Вот возьмите, скажем, топологию и разоблачайте топологические инварианты бесконечномерных пространств.


            1. SpaceOdyssey
              02.02.2017 11:58
              #9860438
              -3

              А вы возьмите свою жену и учите ее щи варить )) Вы откуда так уверены, что знаете КМ лучше меня? И даже если знаете, то не нужно указывать другим, чем им заниматься и о чем думать. Тем более профессиональным ученым. По теме возражайте, если есть что сказать кроме того, что вас раздражает сам факт такой статьи.


      1. vanxant
        01.02.2017 02:52
        #9856744
        +7

        Не, по сравнению с обычным уровнем статей про квантмех всё очень и очень доступно. Нотации в формулах расшифрованы (на чём спотыкаются люди, не изучавшие физику в ВУЗе — формула вроде простая, но как её читать), все участвующие переменные обозваны и объяснены, даны очень дельные пояснения для людей, далёких от темы, например «которые, заметим, принимают значения ±1». В-общем, излагаются не только основы квантовой физики, но и собственно язык изложения.
        Да, это не бульварный детектив, в таких статьях, если вы чего-то не знаете или не понимаете, принято думать над каждой непонятной фразой до просветления. Иначе дальше не поймёте вообще ничего.
        Но так конечно да, картинок маловато, букв многовато…


        1. SpaceOdyssey
          01.02.2017 07:57
          #9856948
          +1

          Спасибо за оценку )) Картинок да, мало, я даже не знал толком, какие именно вставлять. Вставил чисто для украшения. Но здесь картинки мало помогут. Тема серьезная.


      1. SpaceOdyssey
        01.02.2017 07:43
        #9856934
        +2

        Квантовую механику трудно объяснять на пальцах.


        1. Lamaster
          01.02.2017 12:28
          #9857700
          +6

          Потому что палец это объект макромира?


          1. SpaceOdyssey
            02.02.2017 11:54
            #9860424

            Потому что, что идеи КМ не находят аналогий в макромире. Без математики они не постижимы.


      1. Trabant
        02.02.2017 11:54
        #9860430

        я за


    1. ieshevyakov
      01.02.2017 14:11
      #9858116
      +2

      В доступной форме? Вы издеваетесь?


      1. SargeT
        06.02.2017 23:39
        #9870128
        +1

        Ну, парой красивых художественных картинок автор таки статью разбавил, видимо о доступной форме он не издевается :)
        А если серьёзно, аудитория у подобного произведения, конечно, и не должна быть сильно большой, но тут, кажется, перебор. Во времена МИФягИ бы осилил :)


  1. zookko
    01.02.2017 00:47
    #9856594
    -6

    Непривычно много матана для гиктаймс.


    1. zookko
      01.02.2017 10:30
      #9857320
      +3

      Вот так вот. Удивись появлению серьёзной статьи в нынешнем засилье реклам смартфончиков, статей гуманитарий-style — и получай кучу минусов.


      1. SpaceOdyssey
        02.02.2017 12:01
        #9860450

        Спасибо за оценку статьи. В том-то и дело, что статья и тема намного серьезнее, чем думают многие энтузиасты квантовых компьютеров.


  1. qbertych
    01.02.2017 01:33
    #9856652
    +14

    Ну давайте по пунктам.


    Про ЭПР. Тут вы просто придумали какую-то свою квантовую механику с преферансом и профурсетками и пытаетесь убедить нас в ее неправоте. У вас там, простите, в конце появляются члены вида фnum, у которых изначально были строго нулевые вероятности.
    (Это не говоря о том, что фnun, разумеется, являются собственными функциями стационарного гамильтониана в реальных экспериментах — никто не измеряет запутанность поляризации одного фотона с размером обуви другого.)


    Про скрытые параметры.


    Скрытые параметры есть и тогда измерения одной из подсистем могут влиять на другую.

    WTF? Скрытые параметры — это не про влияние, это про предопределенность результата. Берем пару ботинок, отправляем один в Москву, другой в Питер. При этом один из них уже левый, а другой — уже правый. В отличие от запутанных частиц, которые еще не определились.


    Про Аспе. Не обсуждая сферическую волну и КЭД, рискните посчитать то же самое для современных экспериментов (длительность импульса 1 пикосекунда, расстояние меджду импульсами 12 наносекунд, джиттер детекторов 4 пикосекунды).


    1. SpaceOdyssey
      01.02.2017 09:14
      #9857110
      -5

      Если желаете обсуждать тему содержательно, то не паясничайте пожалуйста в дальнейшем, а пишите по существу. Если же угодно паясничать (преферанс и профурсетки), то я вам препятствовать не смею, но реагировать на кривляния впредь не стану.


      Далее, я никого не пытаюсь убедить в неправоте квантовой механики, не передергивайте. Я люблю эту науку и, смею надеяться, знаю и понимаю ее не хуже вас. Конечно сугубо в теоретическом аспекте — опытами в т.ч. численными не занимался. Речь о другом. Если вы еще не поняли о чем, то прочитайте статью внимательно еще раз. И бросьте свой митинговый пафос со словом "нас". Говорите от своего имени пожалуйста. Спокойно и по существу. Впрочем опять же, запретить вам оный пафос не могу. Просто переживаю за Вас — вдруг свалитесь с броневика ))


      А теперь давайте по пунктам, если угодно.


      Про ЭПР Статью Einstein A., Podolsky B., Rosen N., Can Quantum-Mechanical Description of Physical Reality Be Considered Complete прочитайте для начала. Вот перевод на русский http://ufn.ru/ufn36/ufn36_4/Russian/r364_b.pdf. Обозначения взяты оттуда.


      Фраза "в конце появляются члены вида \phi_n\u_m, у которых изначально были строго нулевые вероятности" Почему у них изначально были нулевые вероятности? Это вам так хочется, считая пару изначально запутанной. Но для двух физически независимых систем волновая функция является произведением волновых функций по отдельности. Вероятность произведения независимых событий равна произведению их вероятностей. Ноль может получиться, только если есть нулевой сомножитель.


      Дальше: откуда известно, что \phi_n u_n есть собственная функция гамильтониана системы двух частиц?
      Посмотрите еще раз, как появились эти функции. Изначально собственными были только u_n, а функции \phi_n есть просто коэффициенты ряда Фурье. В частности, как показано ниже, a'priori возможен случай, когда все
      \phi_n равны между собой и представляют НЕ стационарное состояние второй системы. Так что ничего здесь не разумеется.


      Про скрытые параметры. Статью Белла прочитайте для начала http://www.drchinese.com/David/Bell_Compact.pdf. И тогда поймете, что я имел ввиду. Про ботинки звучит красиво, такой стиль хорош для популяризации. Но я предпочел бы более формальный язык, чтобы не упражняться в сетевом краснобайстве, а говорить по существу.


      Про Аспэ Сначала рискните описать эксперимент. Потом я рискну его объяснить. Пока не вижу, чем эксперименты с импульсом в 1 пс и интервалом в 12 нс хуже. Напротив — лучше в плане того, что пара детекторов реагирует на один фотон, а не на пару. Впрочем, вы внятно не объяснили, что там происходит, поэтому жду описания эксперимента.


      1. Eol
        01.02.2017 13:05
        #9857836
        +7

        Я начал только про ЭПР, и у меня уже возникла тонна недоумения.


        У ЭПР вообще-то начальная волновая функция вовсе не в виде \Psi_1(x_1)\Psi_2(x_2) — ведь именно такие волновые функции как раз означают отсутствие запутанности. Если у вас волновая функция представляется в виде ряда (первая формула), то она автоматически не представляется во втором виде — для которого, безусловно, ваше рассуждение работает.


        Касательно рассуждений про коммутацию S с гамильтонианом, и, как следствие, неизменность волновой функции. Вы ведь измеряете S_1, а не полный S; и построенная вами волновая функция не является собственной для S_1. Если бы вы мерили полный спин — то, конечно, ничего бы не изменилось. А иначе ваше рассуждение, мягко говоря, очень странно звучит.


        У меня вот глубокое удивление вызывают попытки доказать несостоятельность квантовой механики (или классических парадоксов оной), используя уже установившийся за сотню лет формализм этой самой квантовой механики.


        1. geisha
          01.02.2017 16:48
          #9858642

          Тоже подпишусь здесь. Какой смысл рассуждать о запутанности если волновая функция — прямое произведение чистых квантовых состояний? Потом автор все-таки рассматривает запутанное состояние |12> + |21>. Но предлагает нам умножить на оператор полного спина системы. Вообще, это отдельная тема для разговора — а как квантовомеханическое измерение проходит? В данном случае мы должны поставить условие, что

          а) оператор действует только на подпространство нашей уже незамкнутой системы
          б) в результате действия оператора система переходит в чистое состояние для одной из частиц, к примеру a*|11> + b*|12> + 0*|21> + 0*|22> или 0*|11> + 0*|12> + c*|21> + d*|22>

          Оказывается, что комбинация этих двух условий автоматически гарантирует, что для начального состояния |12> + |21> в вышеозначенных исходах a = d = 0. Для эрмитовых операторов, конечно. Следовательно, конечное (чистое) состояние — это либо |12> либо |21>. Это и есть запутанность.

          Для неэрмитовых операторов — можно сделать все что угодно. Это означает, что мы разрушаем запутанность.


          1. SpaceOdyssey
            02.02.2017 12:17
            #9860480
            -2

            Автор рассуждает вот как )) Берем изначально запутанное состояние (автор не отрицает явление запутанности, как таковое, основанное на понятии симметричных/антисимметричных состояний тождественных частиц, он лишь отрицает физическую реальность запутанных состояний для заведомо не взаимодействующих систем, т.е., автор отрицает квантовую магию). И дальше частицы разбегаются на бесконечность. И тогда, как рассуждает автор, измерение состояния одной из частиц, если истолковывать его, как измерение комбинированной системы, не повлечет за собой изменения ее состояния, которое вызвало бы изменение состояния второй частицы. Вместо этого, как полагает автор, совместное и изначально запутанное состояние разрушается при измерении одной из частиц. Более, оно перестает быть запутанным уже тогда, когда частицы удаляются друг от друга достаточно далеко. Так что слогикой у автора все в порядке )) Хотя объяснил в статье все это слишком лаконично может быть.


            Дальше я не совсем понял. Какое подпространство уже незамкнутой системы? Да, в результате измерения одной из частиц система перейдет в ее собственное состояние. Конечно! Но и все на этом. Со второй частицей ничего не произойдет.


            Неэрмитовы операторы не соответствуют наблюдаемым, физическим величинам. О них вспоминать не стоит.


            1. mayorovp
              02.02.2017 12:36
              #9860540

              И тогда, как рассуждает автор, измерение состояния одной из частиц, если истолковывать его, как измерение комбинированной системы, не повлечет за собой изменения ее состояния, которое вызвало бы изменение состояния второй частицы. Вместо этого, как полагает автор, совместное и изначально запутанное состояние разрушается при измерении одной из частиц. Более, оно перестает быть запутанным уже тогда, когда частицы удаляются друг от друга достаточно далеко.

              А где доказательство?


            1. geisha
              02.02.2017 13:42
              #9860782

              оно перестает быть запутанным уже тогда, когда частицы удаляются друг от друга достаточно далеко.
              На малых расстояниях запутанность, все-таки, возможна? Каких это расстояниях?
              Какое подпространство уже незамкнутой системы?
              Подпространство одной из двух частиц.
              система перейдет в ее собственное состояние
              Собственное состояние какого оператора? Если оператор — локальный, то собственные состояния — вырождены и состояние второй частицы предопределено не будет.
              Со второй частицей ничего не произойдет.
              Что значит — не произойдёт? Её матрица плотности, конечно же, изменится. Но в широком смысле — да, не произойдёт: как была удаленной невзаимодействующей частицей, так и осталась.
              Неэрмитовы операторы не соответствуют наблюдаемым, физическим величинам.
              Ну не соответствуют, но оператор эволюции exp(i H t) вполне себе неэрмитов и как раз-таки определяет изменение волновой функции при измерении.


            1. Eol
              02.02.2017 17:13
              #9861392
              +2

              Если вы подходите к вопросу с физической точки зрения, а не с точки зрения формализма квантовой механики — то ОК. Вопрос о создании пространственно-разнесённой запутанной системы — это содержательный вопрос, в связи с явлениями дефазировки и декогеренции и взаимодействию с окружающей средой. Сделать это действительно очень сложно, и именно поэтому окружающие нас макроявления классичны. В большинстве случаев запутанность действительно пропадёт, если частицы разнести в пространстве. Но для исследования этого вопроса приведённых вами рассуждений, безусловно, недостаточно; более того, научное сообщество в этом вопросе тоже очень далеко продвинулось, и вам было бы полезно изучить эту область человеческого знания для понимания проблем, связанных с запутанностью.


              Беда лишь в том, что экспериментаторы в различных условиях эти проблемы научились решать, и запутанность таки наблюдают.


              1. geisha
                02.02.2017 17:29
                #9861434
                +1

                Просто дополню: 100 км.


        1. SpaceOdyssey
          02.02.2017 11:43
          #9860390
          -2

          В своем рассуждении к парадоксу ЭПР я предложил разумную альтернативу выводам его авторов. Имея ввиду показать, что их рассуждение является логически необоснованным. Мое рассуждение по поводу волновой функции в ЭПР основано на предположении, что бесконечно удаленные системы физически независимы. И тогда, как я утверждаю, запутанность отсутствует. В этом, собственно, основной тезис моей статьи. Ваше же утверждение:


          "У ЭПР вообще-то начальная волновая функция вовсе не в виде \Psi_1(x_1)\Psi_2(x_2) "


          не основано ни на чем кроме устоявшейся веры в то, что частицы, о которых идет речь в ЭПР, являются запутанными. Утверждение авторов ЭПР о том, что члены этого ряда суть собственные состояния комбинированной системы, на мой взгляд, также не обосновано ничем. И теперь вы мне предъявляете, как факт, что там это имеет место быть? С логикой проблемы.


          Вы просто не разобрались со спином. Я измерил именно суммарный спин пары электронов и нашел его равным нулю (с веротяностью 1 разумеется). Именно поэтому состояние суть собствение для спина. Только я обозначал его не S, а M_z. Просто прочитайте внимательнее, тогда не будет звучать странно.


          Насчет попыток доказать несостоятельность квантовой механики вы просто передергиваете. Разве я использую не аппарат квантовой механики, а что-то иное? Я не подвергаю квантовую механику ни малейшему сомнению. Вы видимо не заметили, что основными источниками для меня являются Дирак и Гейзенберг. Также опираюсь на КЭД, хотя знаю ее хуже. Но достаточно для получения тех выводов, к которым я пришел. Просто не путайте квантовую механику с квантовой магией, основанной на произвольных спекуляциях вокруг ее формализма и, как я думаю, неверной интерпретации опытов Аспэ и других с т.н. запутанными фотонами. Хотя, если вы постигали КМ из книжек по квантовым компьютерам, то для вас вся квантовая механика сводится к рассуждениям о состояниях запутанных кубитов,.достаточным для разработки алгоритмов. И тогда да, я ее опровергаю ))


          1. Eol
            02.02.2017 17:06
            #9861368
            +1

            Безусловно, измерение суммарного спина не изменит эту волновую функцию, но это ничего не доказывает. Существенно именно то, что будет происходить с ВФ после измерения, связанного именно с одним из спинов.


            Я не изучал квантовые компьютеры; впрочем, вы почему-то в этом обвиняете уже не первого человека в комментариях, что довольно странно.


      1. qbertych
        01.02.2017 13:36
        #9857980
        +6

        В реальном мире и фи, и у — собственные функции. Потому что у обоих фотонов мы измеряем поляризацию. (И это без обсуждения всей остальной математики.)


        Нарушения неравенств Белла подразумевают, что если есть скрытые параметры — то должен быть и физический механизм нелокального взаимодействия. Не может быть (как вы пишете), а должен. Не запутанность-вероятность, а физическая сущность, которая перевернет вторую частицу так, как нужно. Со сверхсветовой скоростью, да.


        Про эксперименты — это смешно. Вы нас убеждаете в несостоятельности КМ, и вы же не в курсе современных экспериментов?? В прошлом году и Nature, и APS, и кто только не писал про loophole-free tests.


        (А работы с mode-locked лазерами и down-conversion, которые я упомянул, еще старее — можете начать с этой)


        1. SpaceOdyssey
          02.02.2017 12:50
          #9860576
          -1

          "В реальном мире и фи, и у — собственные функции. Потому что у обоих фотонов мы измеряем поляризацию. (И это без обсуждения всей остальной математики.)"


          Лучше бы вы обсуждали математику, потому что написали какую-то бессмыслицу. Мне нечего здесь комментировать, если не съезжать на стеб


          То, что пишите по поводу скрытых параметров — это и есть альтернатива б) в моей статье. Но есть еще альтернатива а). Чему вы возражаете? Cлово "может" вам не понравилось. Когда сказать нечего, то и это сгодится ))


          Насчет попыток доказать несостоятельность квантовой механики вы просто передергиваете. Разве я использую не аппарат квантовой механики, а что-то иное? Я не подвергаю квантовую механику ни малейшему сомнению. Вы видимо не заметили, что основными источниками для меня являются Дирак и Гейзенберг. Также опираюсь на КЭД, хотя знаю ее хуже. Но достаточно для получения тех выводов, к которым я пришел.


          Просто не путайте квантовую механику с квантовой магией, основанной на произвольных спекуляциях вокруг ее формализма и, как я думаю, неверной интерпретации опытов Аспэ и других с т.н. запутанными фотонами. Хотя, если вы постигали КМ из книжек по квантовым компьютерам, то для вас вся квантовая механика сводится к рассуждениям о состояниях запутанных кубитов,.достаточным для разработки алгоритмов. И тогда да, я ее опровергаю ))


          И да, я не копался во всех экспериментах. Ничего смешного в этом нет — жизни не хватит на все. По вашему, если я вижу грубую, теоретическую ошибку в рассуждениях Аспэ и его последователей (а именно — фотоны вылетают из атома, будучи в собственном состоянии одновременно импульса и углового момента — некоммутирующих наблюдаемых, осмелюсь пояснить высокому сообществу, которое вы представляете, как "нас"), то я обязан молчать об этом до тех пор, пока не изучу весь массив экспериментов, которые на этой глупости нагромоздились за 30 лет? Может быть еще их повторить?


          Если я вижу ошибку у Аспэ, то я пишу о ней. С другими буду разбираться в другой раз. Про down-conversion в курсе. По-видимому там фотон делится на два луча, а не распадается на два фотона. Но не копался в этих опытах, подумаю как-нибудь на досуге


          Конкретно что мне возражаете? Не тыкайте пальцем в статьи пожалуйста, вот мол там написано, а поясните свою мысль. Иначе не что отвечать. И еще раз прошу: поубавьте спеси, если Вас не затруднит.


          1. Eol
            02.02.2017 17:19
            #9861414
            +3

            Вы же должны понимать, что научный процесс именно так и устроен. Именно чтобы не говорить глупости, или не повторять чужих ошибок, прежде чем заниматься научным вопросом, КРАЙНЕ ПОЛЕЗНО было бы изучить, что же там человечество придумало за эти годы. Хотя бы обзоры, или ключевые статьи в окрестности. Именно так наука-физика и работает, простите.


          1. Eol
            06.02.2017 18:11
            #9869176

            Вчитался в дискуссию чуть более подробно.
            То есть вы предпочитаете физическую передачу информации за пределы светового конуса? Ведь именно такую альтернативу и предлагает неравенство Белла. Но не с этим ли вы боретесь? Не большая ли это "магия"?


            Если вас напрягает "коллапс волновой функции" со скоростью быстрее скорости света (что, конечно, у всех людей, что с этим впервые знакомятся, вызывает неудовлетворение — хотя при этом всегда приговаривают, что ни к какиму реальному влиянию событий за пределами светового конуса друг на друга это не ведёт) — то это уже вопрос из раздела интерпретаций квантовой механики, по большей части — философии.
            В таком случае, предлагаю вам ознакомиться с весьма занятной интерпретацией — субьективной квантовой механикой (и несколько соседних ссылок в том же блоге). Вкратце: достаточно лишь откинуть волновую функцию как объективную реальность, точно так же как и классические функции распределения в статистической физике (не забывая при этом, конечно, что статистика всё-таки квантовая, и живёт она всё-таки по иным законам) — и всё встаёт на свои места. И, как у большинства интерпретаций, все наблюдаемые физические явления подчиняются стандартному аппарату оной, и поэтому эта идея, как и большая часть иных интерпретаций, не является фальсифицируемой.


    1. Seven-ov
      01.02.2017 09:15
      #9857114
      +1

      В отличие от запутанных частиц, которые еще не определились.

      А с чего вы взяли, что они еще не определились? Ведь по той же логике ботинок в коробке тоже не определился и постоянно превращается то в левый то в правый, пока мы на него не посмотрим, а когда посмотрим — его состояние фиксируется.

      Передача информации быстрее скорости света возможна (в философском смысле), но механизм некоторыми людьми не верно воспринимается. Пример с теми же ботнками, если второй ботинок отправить за несколько световых лет от нас, при желании мы можем мгновенно узнать какой там ботинок на Альфа-Центавре заглянув в коробочку со вторым ботинком. И вот, вроде ботинок за много световых лет от нас, а мы раз, и узнали все о нем за мгновение. Смысл в том, что мы не можем повлиять на этот выбор (как и повлиять на квантовую частицу, котрая «определилась» в своем состоянии), что в принципе не позволяет нам наладить передачу информации в классическом смысле. А во многих статьях пришут чуть ли не о полнодуплексной связи быстрее скорости света…


      1. niknamezanat
        01.02.2017 15:41
        #9858424

        А с чего вы взяли, что они еще не определились?

        Неравенства Белла и экспериментальная проверка Аспэ утверждают, что не определились до самого последнего момента измерения, в отличии от ботинка, который изначально правый или левый.
        Поэтому информация от того ботинка, который вы посмотрели должна каким-то образом квантово телепортироваться к тому что на Альфе-Центафра


        1. Seven-ov
          01.02.2017 16:22
          #9858538
          -1

          Только о проведенных эксперементах с однозначными выводами я пока не слышал. Отсюда и скепсис.


  1. laughing_one
    01.02.2017 01:52
    #9856702

    Друзья, я совершенно не специалист в этой области, и пользуясь случаем, позвольте задать пару вопросов, вдруг кто доступно ответит:

    1. Что такое спин?
    Определение в вики я читал, но не понял его. Как-то наглядно можно его представить?

    2. Как связать 2 электрона (фотона или чего)?
    Не понимаю, что такое связанность (сцепленность) и как этого добиться. Определение в вики тоже читал, но тоже не понял.


    1. abstracto
      01.02.2017 03:03
      #9856758
      -4

      1. грууубо говоря если луна у земли — это электрон, то спин это то в какую сторону она вращается вокруг своей оси. у фотона тоже 2 состояния спина.
      2. загнать их в очень узкое пространство, а потом дать разлететься в разные стороны. при этом не возможно знать какой именно полетит в какую сторону. как только спин одного из фотона будет измерен — автоматически становится известен спин второго.


    1. Mulin
      01.02.2017 21:36
      #9859340

      1 Неясные определения всегда сбивают с толку. Если представить себе частицу как шарик, то спин, это вращение шарика, где ось вращения располагается вдоль траектории движения. Соответственно есть правосторонний и левосторонний спин. Частицы в квантовой физике не рассматриваются как буквально очень мелкие шарики. Подразумевается что это некий квантовый объект не имеющий конечной длинны (если не брать струнные и иные теории). Соответственно вращение этого квантового объекта тоже некое свое — квантовое. Легко понять сложность и запутанность определения, уяснив один важный момент — реальный шарик не мог бы вращаться в соответствии с параметрами спина по той причине, что тогда скорость углового движения поверхности этого шарика, превысила бы скорость света, что есть парадокс. Однако спин имеется, а частицы, согласно Копенгагенской Интерпретации не есть шарики, а по сему спин, это некое внутреннее квантовое состояние. А сейчас вообще опасная для мозга штука будет. Вы то неверно слышали о числе спина — 1, 1/2, 2. Так вот, если очень грубо, это число означает количество оборотов, которое должна совершить частица, что бы вернуться в исходное состояние. Если с 1 оборотом все ясно-понятно, то вот два оборота уже вызывает вопросы, что уж говорить о половине оборота и ты уже вроде как полностью обернулся 0_о
      2 Родить их вместе. Например излучить лазером.


      1. laughing_one
        01.02.2017 22:15
        #9859404

        Благодарю за разъяснения!

        1. Как раз число спина, о котором я действительно слышал, мне более-менее понятно, не считая того, что понятие спина, несмотря даже на Ваше подробное объяснение, до сих пор представляю смутно…
        Если это некий непредставимый «квантовый параметр» — то почему его принимают именно как за вращение? Тем более, что частицы, как Вы сами упомянули, на самом деле не являются «шариками». Или это чисто номинальное представление?
        Как можно представить спин у электрона, если он таки не шарик? Есть электрон и у него есть некий параметр, который можно измерить, но что это именно — никто не знает, просто для удобства считая за направление вращения? Я прав?

        2. Прочитал принцип действия лазера. Вроде бы стал понятнее. Спасибо!


        1. Kulich
          01.02.2017 23:46
          #9859532
          +2

          Мне кажется что спин это такая же абстракция как аромат и цвет кварков или упаси господь их прелестность. Хотя может меня поправят.


        1. mayorovp
          02.02.2017 09:50
          #9860048

          Любая частица — это волна. Волна может распространяться параллельно (например, плоская)… а может при распространении "закручиваться". Второй вариант — это и есть спин.


          Обнаруживается он по моменту импульса или инерции.


        1. Nathanson
          02.02.2017 11:51
          #9860414

          Спин еще измеряют, пропуская частицу через призму (стеклянный прозрачный куб). Если у нее один спин, то она пролетит по прямой через призму, если другой спин, то она под углом 90 градусов отразится и вылетит из призмы в другом направлении.


  1. abstracto
    01.02.2017 02:40
    #9856728

    del


  1. DmitriyN
    01.02.2017 08:59
    #9857078
    +8

    У Вас, по-видимому, какое-то сове особое понимание запутанности, с которым Вы спорите. Можно начать с того, что в реальном мире, независимость квантовых объектов не влечет за собой сепарабельность, как в классике — это то, что и приводит к «квантовости» квантовой механики.
    Вы же, написав \Psi(x_1, x_2) = \Psi_1(x_1) \Psi_2(x_2), автоматически предположили сепарабельность. Все дальнейшие выводы основаны на этом. Кроме того, ваше утверждение о том, что (|1, 2> + |2, 1>) превращается в |1>*(|1> + |2>) напрямую противоречат любому набору аксиом квантовой механики или отсутствию дальнодействия — у вас поменялось expectation value оператора у суммарной системы.


    1. SpaceOdyssey
      01.02.2017 09:40
      #9857176
      -2

      Мое понимание к делу не относится, т.к. как я спорю с вашим пониманием, отраженным в этой фразе про сепарабельность. Я как раз и доказываю, что оно не имеет под собой не только теоретических, но и, если я прав с интерпретацией опытов Аспэ, экспериментальных оснований. Не говоря уже о том, что противоречит здравому смыслу.


      В анализе статьи ЭПР я показываю, что рассуждения авторов были не вполне корректными и с этой целью предъявляю альтенративное рассуждение, основанное на предположении том, что независимые системы являются сепарабельными. Верно он или нет — вопрос открытый. Но поскольку есть логическая альтернатива, рассуждения авторов ЭПР не могут служить твердым фундаментом для пардигмы ЭПР — запутанности.


      Чему противоречит, можно поконкретнее? "Любому набору акстиом квантовой механики" — это вода.
      Чему именно? Cреднее значение момента суммарной системы у меня не менялось. И кстати, там знак минус между векторами, а не плюс, как вы написали. Не поэтому ли у Вас поменялось среднее значение?


      1. DmitriyN
        01.02.2017 09:55
        #9857232
        +1

        Окей, раз несепарабельность выкидываем, то дальше рассуждать про остальной аппарат бесполезно. Или Вы хотите наложить ограничение на допустимые состояния и выбирать их только из сепарабельного подпространства общего гильбертова пространства? Как тогда заставить динамические уравнения не приводить к ним при эволюции?

        По поводу того, что не поменялось среднее значение — конечно, если у Вас начальный спин — 0, то среднее не поменяется. Но что же делать со спином 1 (с плюсиком, как у меня написано)?


        1. DmitriyN
          01.02.2017 10:04
          #9857250
          +1

          Да, забыл задать главный вопрос :). Если все функции сепарабельны, что как же можно писать |1, 0> — |0, 1>?


          1. SpaceOdyssey
            01.02.2017 10:15
            #9857280
            +2

            Я же не отрицаю существование систем из тождественных частиц, подчиняющихся статистикам Бозе-Эйнштейна или Дирака-Ферми или даже каким-то еще. Но эти системы не состоят из физически независимых подсистем. Например, электроны в одном атоме или фотоны в одном поле.


            То есть запутанность, как феномен, свойственный наборам из тождественных частиц, имеет место быть конечно. Но не между физически независимыми системами (скажем бесконечно удаленными). Обратное я и называю ЭПР — запутанностью. Таким образом, я не считаю, что все квантовые системы суть сепарабельные, не приписывайте мне выдуманные вами глупости. И просто не передергивайте, пытаясь подловить на противоречии. Не выйдет, хотя я могу ошибаться, как все люди.


            1. DmitriyN
              01.02.2017 10:31
              #9857326
              +5

              Окей, а чем отличаются «разнесенные» системы от «неразнесенных»? Насколько нужно разделить систему из двух частиц, чтобы «запутанность» превратилась в «ЭПР-запутанность»? Два электрона в одной длинной молекуле ДНК, находящиеся на разных концах еще могут быть запутаны или уже нет?

              P.S. Физически независимых систем не бывает. А если еще вспомнить, что на самом деле, вся квантовая механика полевая, то и непосредственно взаимодействующих электронов тоже не бывает.


              1. niknamezanat
                02.02.2017 09:24
                #9859976
                +1

                Физически независимых систем не бывает

                Почему тогда в (ур.1) говорят об паре образующих «единую» и следовательно независимую систему? На мой взгляд, потому что забывают добавить, что «разнесенные» системы получаются из «неразнесенных» после взаимодействия с какой-то третьей системой.


        1. SpaceOdyssey
          01.02.2017 10:22
          #9857298

          Ничего не выкидываеи, об этом сказано в комментарии ниже.


          С плюсиком с электронами не получится, т.к. они — фермионы.


          Насчет гальбертова пространства кстати. Сразу видно, что сведений о квантовой механике вы набрались из теории квантового компьютинга. Отнюдь не каждое пространство состояний суть гильбертово. Бывают же собственные векторы наблюдавемых с непрерывныым спектром (импульс например). Этих вы в гильбертово пространство не запихнете. И даже просто в пространство со скалярным произведением не выйдет. Гильбертово пространство состояний — это мантра ))


          1. DmitriyN
            01.02.2017 10:56
            #9857390

            С плюсиками с электронами прекрасно получится, если у них отличается что-то еще. На спине свет клином не сошелся. Вы же физически разнесенные системы рассматриваете.

            А Вас что конкретно в гильбертовости беспокоит? Если чисто формальные вопросы, то есть, например, тройки Гельфанда, которые их отлично решают. Если более физические вещи, то, как Вы, кажется справедливо сами замечали, собственные состояния неограниченных операторов все равно физически нереализуемы.


            1. SpaceOdyssey
              02.02.2017 13:05
              #9860626
              -2

              Меня ничего не беспокоит. Просто забавляет, как часто слово "гильбертово пространство" произносят математики, занимающиеся квантовыми вычислениями и толком не изучавшие квантовую механику. Говорю это, как математик ))


              Я справедливо заметил не то, что вы снова мне приписываете. Не извинившись ни разу за предыдущие, поверхностные наскоки. Но я бесконечно с вами терпелив, как видите, поэтому продолжаю. Я заметил, что собственные векторы наблюдаемых с непрерывным спектром не могут скалярно перемножаться между собой, т.к. их "скалярные произведения" имеют смысл только, как обобщенные функции. То есть не то, что гильбертовым, но и просто унитарным пространством, вообще говоря и почти всегда, пространство состояний не является. Реализуемы такие состояние или нет — это другой вопрос. Важно, что их нельзя игнорировать в формализме КМ. Более того, без них от нее ничего не останется кроме квантовых вычислений.


              Мантра о гильбертовом пространстве выдвет квантовых программистов с головой. И вот они-то, как мне кажется, больше всех разглагольствуют об аксиомах и основаниях КМ, которым якобы я противоречу )).


              1. DmitriyN
                03.02.2017 02:43
                #9862208

                Я не хочу с Вами спорить, потому как занятие это довольно бесплодное, но скажите, все-таки, что там происходит с «эпр-запутанной» парой с суммарным спином 1?


  1. interprise
    01.02.2017 09:35
    #9857166
    +1

    Скажите пожалуйста, можем ли мы «одновременно» (быстрей чем скорость света) в точках А и Б получить случайные значения?


    1. SpaceOdyssey
      01.02.2017 09:45
      #9857192

      Я не очень вопрос понимаю ))


      1. interprise
        01.02.2017 09:48
        #9857204

        Проводя изменения к примеру спина фотона, мы не зависимо от расстояния между запутанными фотонами получим к примеру -1/2 и 1/2. Таким образом мы можем мгновенно «передавать» информацию, однако она будет представлять из себя случайную последовательность. Я все правильно понял? когда речь заходит о квантовой криптографии там применяются какие-то сложные схемы, вот меня интересует вопрос просто передавать случайный вектор и делать XOR с данным мы можем или нет.


        1. SpaceOdyssey
          01.02.2017 10:04
          #9857252

          не понимаю все равно. Что такое XOR в курсе )), но остальное… Что значит передать случайный вектор? Передаем одно, а получаем другое и случайное? Вы извините, мне пора уже. Может быть еще вернемся к этому. Про квантовую криптографию и вообще все эти фокусы с запутанностью почитайте здесь, очень доступное изложение, хотя и не научно-популярное http://extremal-mechanics.org/wp-content/uploads/2017/02/RIFFEL.pdf. Отличный текст для ознакомления с основными идеями квантового компьютинга.


        1. wataru
          02.02.2017 13:17
          #9860682

          Можно так сделать, да. Но тут нет никакой передачи информации. Потому что запутанные частицы получаются где-то локально, а потом разносятся в пространстве. Это как написать код на двух бумажках и разнести их очень далеко. Прочитав бумажку в одном месте, мы знаем, что написано в другом месте. Но никакой информации мы не передавали.


          1. interprise
            02.02.2017 13:19
            #9860688

            спасибо за ответ, но хотелось бы пруф. и да стоит заметить, что бумажки условно бесконечные и я и не говорю про передачу информации в привычном нам виде.


            1. plus79501445397
              04.02.2017 19:57
              #9865526

              1. С какой целью Вы хотите применить XOR? Он конечно легко применяется, в качестве проверки Ваших идей я бы посоветовал воспользоваться любым эмулятором квантового компьютера или например, настоящим КК от IBM.
              2. Пусть меня поправят знатоки КМ, но разве для получения

              условно бесконечного
              набора скореллированных случайных значений в удаленных точках А и Б не нужно будет разносить в эти точки
              условно бесконечное
              количество пар запутанных фотонов?


              1. mayorovp
                04.02.2017 21:57
                #9865704

                Нужно. В том-то и идея квантовой криптографии: имея бесконечный поток запутанных частиц от стороннего источника, мы получаем два синхронных генератора случайных чисел с неограниченной энтропией. Надо "всего лишь" убедиться что наш фотон не перехватил никто другой.


  1. SpaceOdyssey
    01.02.2017 09:53
    #9857218
    -2

    Ув. коллеги! Хотел бы попросить некоторых из вас, кто изучал квантовую механику или даже специализируется по ней, слегка убавить спеси и не считать меня полным профаном. Статья http://extremal-mechanics.org/wp-content/uploads/2017/02/Article_Z.pdf, написанная в строго научном стиле (нет варианта на русском языке) поможет вам убедиться в том, что вы имеете дело отнюдь не с любителем, нахватавшимся в интернете по вершкам. Поэтому оставьте пожалуйста чванливые поучения в стиле "учите физику" для других и давайте обсуждать тему по существу. Если же вы не видите предмета для обсуждения, на что имеете конечно право, то и я позволю себе не реагировать на комментарии, которые написаны в стиле, цепляющем мое самолюбие. Однако тема есть ))


    1. Shkaff
      01.02.2017 11:20
      #9857464
      +4

      Как ваше определение запутанности (ур. 2) выглядит для матриц плотности?


      1. SpaceOdyssey
        02.02.2017 13:14
        #9860670
        -2

        Я об этом пока не думал.


        1. Shkaff
          02.02.2017 14:13
          #9860870
          +2

          Было бы интересно, как у вас получится сформулировать это для реального случая. Я тоже не согласен с вашим определением запутанности, и мне кажется, оно не обобщается для матриц плотности.
          Кстати, а почему вы не выкладываете на архив свои статьи?


    1. qbertych
      01.02.2017 13:04
      #9857830
      +5

      Эмм. На первой же странице уравнение 2 — это ваше личное определение запутанности, которое не совпадает с общепринятым, о чем вы сами и пишете:


      Definition 1 for the entangled state of two particles is close to the conventional notion.

      Пока вы не доказали эквивалентность вашего определения общепринятому, разговаривать не о чем.


      1. SpaceOdyssey
        02.02.2017 13:11
        #9860646
        -2

        И не разговаривайте, я вас к этому не принуждаю. Но я и не собираюсь доказывать эквивалентность общепринятому, т.к. считаю, что оно нуждается именно в таком (небольшом) уточнении.


        1. Shkaff
          02.02.2017 14:18
          #9860892

          На самом деле, доказывать эквивалентность не обязательно, но вот объяснить, откуда оно такое взялось — желательно бы. Из статьи этого совершенно не ясно (или я плохо прочитал).


    1. Eol
      01.02.2017 13:34
      #9857976
      +6

      Это связано с совершенно необоснованными нападками на ученых, занимающихся квантовой механикой — якобы, никто из них (sic!) не разобрался с квантовой механикой, не задает себе интересных вопросов и гонятся лишь за статьями. Что это, как не спесь с вашей стороны?


      1. SpaceOdyssey
        02.02.2017 13:20
        #9860692
        -1

        Не врите! Я не писал, что никто не владеет. Ученые бывают разные. Но в среднем теоеретическая поверхностность и тенденция гонки за статьями имеют место быть. Я просто видел много таких статей, на многие писал рецензии. Мое оценочное суждение состояния дел в современной теор-физике — это не спесь. Если так передергивать, то любая критика есть спесь. Можно только дефирамбы петь и втирать обществу очки?


        1. Eol
          06.02.2017 17:25
          #9868978
          +3

          Я не вру, я утрирую. И вы сейчас утрируете.
          Ведь научное сообщество так устроено — достаточно, чтобы хотя бы несколько толковых учёных обратили внимание, что пространственно-разнесённая запутанность, как вы утверждаете, невозможна (=> обосновали это, поставили соответствующие эксперименты, опубликовали результаты) — и этот "пузырь", как вы считаете, лопнул бы. Но, видимо, последние несколько десятков лет научное сообщество находится во власти коллективного умопомешательства и заблуждения. Это мне представляется крайне сомнительным, и на этом суждении я основываюсь.


          Вы правы, учёные бывают разные, и глупо отрицать отсутствие карьеристов в науке. Но где же в таком случае добросовестные учёные? Почему они это упустили? Об ЭПР сейчас знают буквально все, начиная с младших курсов физических ВУЗов. О механизмах, разрушающих когерентность — гораздо меньше, но тем не менее, всё ещё много. По-прежнему много и людей, занимающихся экспериментальной проверкой (до сих пор, хотя столько воды утекло!) — созданием запутанных систем, измерением корреляций, и пр. Среди них нет ни одного настоящего учёного? Где они?


          (позвольте полюбопытствовать, о каком разделе теоретической физики, и о каком журнале (журналах?) идёт речь?)


  1. zuborg
    01.02.2017 10:27
    #9857304
    +2

    В рамках запутанной парадигмы также рассматривают пару фотонов в одинаковых состояниях поляризации, так что общее состояние пары можно задать вектором $c(|1,1\rangle+|2,2\rangle)$, где $|1\rangle$ и $|2\rangle$ задают состояния поляризации в перпендикулярных направлениях. Если при измерении одного из фотонов он перейдет в собственное состояние $|1\rangle$, то якобы это повлечет переход пары в состояние $|1,1\rangle$, т.е., мгновенный скачок второго фотона в такое же состояние поляризации $|1 \rangle$. Однако, аналогично примеру с синглетом электронов можно утверждать, что пара фотонов останется в собственном состоянии $c(|1,1\rangle+|2,2\rangle)$. Это противоречие означает, что измерение одного из двух фотонов разрушает систему, после чего второй фотон остается в исходном состоянии $|1\rangle+|2\rangle$. Запутанности в смысле ЭПР и здесь не возникает.

    Если бы второй фотон после измерения первого оставался в состоянии $|1\rangle+|2\rangle$, то его (второго фотона) измерение давало бы результат 1 или 2 с вероятностью 50/50. Но эксперимент показывает, что при измерении первого фотона в состоянии 1 второй фотон (для Вашего случая) тоже будет измерен в состоянии 1 в 100% случаев (причем независимо от того, в каком порядке и с каким интервалом мы проводим эти измерения).


    1. niknamezanat
      01.02.2017 11:03
      #9857410
      +2

      Как я понял, автор как раз и ставит под сомнение экспериментальные доказательства корреляции.


      1. SpaceOdyssey
        02.02.2017 13:23
        #9860706
        -2

        Да, именно так.


        1. zuborg
          02.02.2017 16:14
          #9861202

          Даже так? Т.е. Вы утверждаете, что если подготовить два запутанных электрона с разнонаправленными спинами, и измерить их (спинов) проекции на одну и ту же ось, то результаты не будут противоположными в 100% случаев? А какими они будут? 50/50?


  1. aleksandros
    01.02.2017 11:40
    #9857554
    -1

    Значит, теперь надо ждать экспериментов, которые однозначно смогут пролить на это свет?


  1. lavmax
    01.02.2017 12:49
    #9857768

    Можно ли измерить спин частицы, не установив его при этом в какое-то свое (измерителя) значение?


    1. SpaceOdyssey
      02.02.2017 13:27
      #9860722

      У него всего 2 значения. В одно из них переходит при измерении. Если частица находится в собственном спиновом состоянии, т.е., уже имеет определенный спин (его проекцию на какую-то ось), то при достаточно аккуратном измерении в нем же и останется. То есть ответ на Ваш вопрос положительный.


      1. lavmax
        04.02.2017 02:19
        #9864622

        А если мы измерим недостаточно аккуратно, то квантовая запутанность разорвется?


  1. kauri_39
    01.02.2017 13:51
    #9858048
    -3

    По-моему, если бы сомнения автора были оправданы, то не было бы никакого производства квантовых компьютеров с мгновенным взаимодействием кубитов, ни квантовой криптографии. Это уже не исследовательские проекты, а промышленные. И вообще, существование мгновенной связи следует из общего закона эволюции материи.


    1. SpaceOdyssey
      02.02.2017 13:33
      #9860732

      А его и нет. Есть только мечты об этом и проекты. Реально работающих устройств, использующих механизм квантовой запутанности, на мой взгляд не существует. Скажем, компьютер DWAVE не есть квантовый, хотя он использует элементную базу на квантовых эффектах. Вот интересный комментарий на эту тему: http://extremal-mechanics.org/archives/18241#comment-4020


  1. Alexsandr_SE
    01.02.2017 16:20
    #9858532

    Один вопрос. Квантовая запутанность это «левый и правый ботинок» отправленные в разные места и там осмотренный хотя бы один из них или эти «ботинки» еще реально не определились?
    в первом случае состояние частиц жестко задано в момент создания, но какие именно у другой частицы можно узнать только после замера (та же пара ботинок отправленная не глядя), во втором случае что-то непонятное.


    1. zuborg
      01.02.2017 16:34
      #9858570
      +3

      Первый случай — это наличие скрытых параметров, проявляющихся через правость или левость ботинка в Вашем случае.
      Второе — это отстуствие скрытых параметров — результат измерения определяется в момент собственно измерения, а не генерации состояния. А запутанность проявляется в том, что результаты двух (или больше) измерений скоррелированы друг с другом (если один ботинок правый, то второй — левый, и наоборот).

      Экспериментально подтверждено (см. Неравенства Белла), что природа работает по второму варианту.


      1. Kulich
        01.02.2017 23:53
        #9859542

        В подобных статьях для чайников как-раз не хватает объяснения простого этих самых неравенств. Как получается что мы не измеряли, но уверены что частица неопределившаяся? Желательно и не рода «вот из этого элементарного уравнения следует»


        1. mayorovp
          02.02.2017 10:12
          #9860138
          +1

          Это будет затруднительно. Для объяснения "на пальцах" потребуется чтобы у ботинок было 3 независимых параметра, причем мы должны быть способны после открытия коробки определить только один из них на наш выбор (либо линейную комбинацию параметров).


          Вряд такие странные ботинки будут понятны.


          1. Kulich
            02.02.2017 21:57
            #9861930

            Аналогии с ботинками как раз сбивают с толку =) Вот человек объяснил ниже, не скажу что я понял, но суть в целом уловил.


        1. zuborg
          02.02.2017 17:16
          #9861404
          -1

          Грубо говоря — если есть скрытый параметр, который предопределяет результат измерения, тогда для трех осей A, B, C результат измерения каждой частицы из запутанной пары будет предопределен в момент генерации такой пары — например <-,+,-> для первой частицы и <+,-,+> соотв для второй (рассматриваем разнонаправленные спины). Т.е. всего 8 вариантов. Так вот, если сделать замеры по разным парам осей (частиц то две) много раз, то есть вот такое соотношение вероятностей (одно из):
          P(A+,B+) <= P(B-,C-) + P(A+,C+)
          которое должно выполняться, если эти 8 вариантов равновероятны. Для любых направлений осей.

          Но в квантовом случае есть комбинация углов между осями, когда это соотношение не будет выполняться. Экспериментально подтверждено, что оно действительно нарушается. Т.е. результат измерения не предопределен до момента измерения.


  1. Tertium1
    02.02.2017 12:31
    #9860514
    +1

    Спасибо за статью. Но все же — как тогда быть с коммерческими системами квантовой криптографии? Куча народа ими занимается и вроде бы даже их используют конечные пользователи. Я могу предположить, что запутанность слишком обывательски интерпретирована, как кот Шредингера и корпускулярно-волновой дуализм, что неверно использовать интуитивные понятия для описания процессов, для которых у рас нет аналогий. Но если коммерческая система работает, обычно это означает, что хотя интерпретации и нужны публике, даже в их отсутствие открытые закономерности позволяют усмешно прогнозировать и выстраивать действующую технологию. Например, мало кто может представить кватернион, но мы ими отлично пользуемся. Или многомерный OLAP куб не требует вообще говоря многомерного мышления и магии. Так неужели в запутанности вообще ничего нет? И эти системы — то же, что DWAVE для квантового компьютинга?


    1. SpaceOdyssey
      02.02.2017 13:39
      #9860762
      -1

      Насчет коммерческих систем квантовой криптографии нужно разбираться. Но вроде бы там нет квантовой запутанности в смысле ЭПР. Думал об этом, но забыл уже, что думал. Попробую Вам позднее ответить (дней через несколько может быть). Пока посмотрите пожалуйста мой комментарий по поводу китайского якобы радара, использующего ЭПР — запутанность. На мой взгляд — развод по китайски http://extremal-mechanics.org/archives/18241#comment-4020.


    1. SpaceOdyssey
      02.02.2017 13:39
      #9860766

      Да, и спасибо Вам за оценку статьи ))


    1. Tertium1
      03.02.2017 12:14
      #9862882

      Прошу прощения, конечно, рас=нас, усмешно=успешно. Экранная клавиатура, «очень трудно копытом номер набирать» (с)


  1. erwins22
    02.02.2017 12:31
    #9860516
    -2

    вот такой мысленный эксперимент

    пускаем 2 запутанных фотона один в Токио, второй в Нью-Йорк.

    мы хотим передать из Нью-Йорка в Токио 1 бит. Для этого опредяляем поляризацию фотона в Нью-Йорке. Фотон отправленный в Токио пока не дошел.

    Далее мы пускаем фотон пришедший в Токио в полуфильтр (1 фильтр 50% прохождения горизонтальной поляризации и 100% вертикальной, 2 фильтр 50% прохождения вертикальной поляризации и 100% горизонтальной)
    если фотон имеет определенную поляризацию, то он пройдет систему с вероятностью 50%

    а вот в случае запутанности вероятность будет другая?

    посылаем одновременно 1000 фотонов и с определенной вероятностью передаем информацию мгновенно.
    При этом нарушается принцип ограничения скорости передачи информации, но не нарушается ограничение на перенос материи.


    1. zuborg
      02.02.2017 16:10
      #9861192
      +1

      а вот в случае запутанности вероятность будет другая?

      Не будет. Запутанные состояния в плане вероятности измерения любой частицы никак не выделяются от незапутанных состояний этих частиц, вообще. Запутанность проявляется исключительно в скоррелированности результата измерения одной частицы с результатом измерения второй частицы из пары (если оси измерения совпадают, а спины противонаправленны — то корреляция -100%, например).


  1. prostovovan
    02.02.2017 13:41
    #9860776
    -2

    Так путешествия во времени возможны или нет?


    1. SpaceOdyssey
      02.02.2017 13:43
      #9860786

      В будущее можно в силу эффектов ТО )).


    1. erwins22
      02.02.2017 14:03
      #9860848

      В прошлое в ОТО возможны, в квантовой механике нет.


      1. SpaceOdyssey
        04.02.2017 01:48
        #9864604
        -1

        Невозможны в ОТО путешествия в прошлое. Только в спекуляциях на основе ОТО вроде кротовых нор. В фильме "Интерстеллар" возможно. В самой ОТО этого нет.


        1. erwins22
          05.02.2017 13:56
          #9866336
          -1

          самой ОТО это есть.
          Кстати, есть теория которая объясняет квантование на основе того, что не все варианты «будущего» могут возникнуть в силу путешествия информации в прошлое.
          Так как такие теории сложны, то их исключительно сложно опровергнуть или подтвердить.
          Но проблема таких теорий в том, что они работают в пространстве времени определенным исходным искажением метрики.


          1. SpaceOdyssey
            05.02.2017 23:41
            #9867072
            -1

            Вы ошибаетесь. Я знаю, что такое ОТО прилично без ложной скромности. Все-таки это — риманова геометрия + тензорный анализ. Родная для геометров стихия. Нет там таких эффектов. А вот на основе ОТО есть много спекуляций (теоретических построений без связи с физ. реальностью), где возможно всякое.


            1. erwins22
              06.02.2017 09:46
              #9867462
              -1

              Вы правы. ОТО — «риманова геометрия + тензорный анализ». Вы правы — «А вот на основе ОТО есть много спекуляций (теоретических построений без связи с физ. реальностью), где возможно всякое. „

              И я прав. “ Кстати, есть теория которая объясняет квантование на основе того, что не все варианты «будущего» могут возникнуть в силу путешествия информации в прошлое.»

              Это одна из хреновой тучи альтернатив. Причем какая из них верна пока никто не может даже представить.

              Может мы верна теория торсионных полей (Энштейна-Катрана) где нет сингулярностей, есть сверхсветовая передача информации и эта теория по эксперементальным данным находится в числе допустимых.


            1. R9A_019
              06.02.2017 23:40
              #9870132

              На счет эффектов и спекуляций, насколько мне известно, процессы динамического образования объектов вроде "кротовых дыр" в рамках ОТО, уже разъяснены, на сколько я помню вводится специальный формализм, благодаря оному и становится видно, пусть и теоретическое, но обоснование их возможного существования и возникновения (а также условий возникновения). Cсылку так сходу не дам, но натыкался на неё на форуме dxdy, когда господин Munin выразил нечто подобное. Далее, есть такая замечательная книга (С.В. Красникова Некоторые вопросы причинности в ОТО -М.: Ленанд, 2015 -336 с.) где обсуждается ограничения перемещения во времени (но не отсутствия оной возможности). Можете глянуть. Ну теперь про статью, вопросов нет, несколько затянута, но это не существенно. Вообще чем больше о КМ напишите, тем лучше, идеального описание не найти, а так хотя бы с разных изложений можно выяснить суть.


  1. Macilnor
    02.02.2017 16:05
    #9861180

    Замечательная статья. Правда читалось сложно и я не совсем уверен что все правильно понял, но мне понравилось. Побольше бы такого.


    1. SpaceOdyssey
      04.02.2017 01:36
      #9864592
      -1

      Спасибо за Ваш позитивный отзыв в потоке поверхностной критики ))


  1. SpaceOdyssey
    04.02.2017 01:42
    #9864600
    -1

    Извиняюсь перед теми, кому пока не смог ответить. Весь день готовил новую статью на эту тему, хотя научный материал не новый (но лично мой). Постараюсь ответить позднее, хотя не всем хочется отвечать. Надоели кавалерийские наскоки с глупостями вроде того, что я отвергаю квантовую механику ))


    Новая статья посвящена той же проблеме, но уже в контексте квантовых компьютеров https://geektimes.ru/post/285490/. Там речь идет о кубитах. Должна быть интересна даже тем, кто о них толком не знает. Узнает значит )) На многие вопросы, которые мне здесь задают, я постарался в ней ответить.


  1. timapple
    05.02.2017 08:14
    #9865984

    SpaceOdyssey Дмитрий Борисович, спасибо за статью. Хочу узнать Ваше мнение о такой интерпретации КМ: КМ есть предельный случай КТП для сильно разряженных полей (когда можно говорить об единичных квантах). Вот небольшое эссе об этом Препарата Дж. Реалистическая квантовая физика. 2005 год. 124 стр. Там есть упоминание об ЭПР-парадоксе. Объясняется тем, что КМ, как предельный (упрощенный) случай, не может объяснить вещи, требующие более общей теории (КТП). Рекомендую прочитать всем интересующимся КМ/КТП. Даже чтение «между формул» дает лучшее понимание связи этих теорий.


    1. SpaceOdyssey
      05.02.2017 11:44
      #9866160

      Спасибо на добром слове. Я слабо знаком с КТП, поэтому мнения у меня никакого нет по Вашему вопросу. Но что касается КЭД, то из нее КМ никоим образом не может быть получена в предельном случае. Эссе гляну, но самое название текста — "эссе" уже не нравится ))


  1. realbtr
    05.02.2017 15:08
    #9866418
    +1

    Автор — фрик, рассматривающий лишь математический формализм и полагающий, что классическая физика, с глобальными концепциями пространства-времени имеют приоритет на другими. Не понимая даже азов квантовой механики автор путает причины и следствия и спорит с причинами, опираясь на неоднозначность формальных следствий (видимо не вкурсе о неполноте и противоречивости формальных систем). Это не лечится.


    Но один вопрос задам. С чего автор решил, что нормальным является классическое состояние определенности, а не квантовое состояние запутанности?


    Отталкиваясь от ошибки — ошибок не избежать. Начните с другого конца: определенность имеет условия, запутанность — безусловна.


    Впрочем, уверен, что это не поможет. Убежденность фриков маниакальна.


    1. SpaceOdyssey
      05.02.2017 23:44
      #9867074
      -1

      А вы — дурак и хам. Когда научитесь вести корректную дискуссию, тогда и поговорим по существу. Вот только вряд ли вы когда-нибудь научитесь. Да и сказать вам нечего, т.к. несете околесицу. Продолжайте паясничать, клоун.