Один мой друг любит говорить (не знаю, его это слова или он их где-то взял), что в программисты идут по двум причинам: если ты хочешь стать хакером или если ты хочешь писать игры. Мой случай второй. Всегда интересовался разработкой игр, причём той частью, которая отвечает за искусственный интеллект в играх. Очень много времени я потратил на изучение алгоритмов поиска пути. Реализуя очередную версию алгоритма A* на Java, столкнулся с интересной ситуацией, связанной с коллекциями TreeSet и TreeMap.

Сразу хочу ввести два понятия, которые буду использовать на протяжении всей статьи: поиск по равенству и поиск по сравнению. Поиском по равенству я буду называть поиск в коллекции, где для сравнения элементов используются методы equals и hashCode. Поиском по сравнению или поиском на основании сравнения я буду называть поиск элемента в коллекции, где для сравнения элементов используются методы compare и compareTo.

В алгоритме A* используется две коллекции для хранения точек пути: открытый список и закрытый список. Точка пути, грубо говоря, имеет для нас три важных атрибута: координату X, координату Y и значение метрической функции – F. Для закрытого списка необходимо выполнять только две операции добавление и поиск. С открытым списком всё несколько сложней. С открытым списком помимо операций добавления и поиска элемента необходимо также находить наименьшую точку по значению метрической функции.

Для закрытого списка выбираем HashSet тут всё очевидно, для операций добавления и поиска отлично подходит, если конечно вы написали хорошую хэш-функцию. С выбором коллекции для открытого списка возникают затруднения. Если выбрать HashSet, как и для закрытого списка, то мы получим наилучшую асимптотику для операций вставки, поиска и удаления – O(1), однако поиск минимального будет выполняться за O(n). При выборе TreeSet или TreeMap мы будем иметь O(log(n)) для вставки и поиска, но для поиска и удаления минимального будем иметь всё те же O(log(n)). Посмотреть асимптотики различных коллекций можно тут.

Ещё одна важная деталь, связанная с TreeMap и TreeSet – все операции с этими коллекциями используют сравнения. Таким образом, если поиск нас интересует с учётом координат точек, то для поиска минимального мы используем значение метрической функции, а это приведёт к тому, что операция может быть не выполнена для точки, у которой изменили это значение. Более того при вставке новых значений мы можем получить некорректно построенное дерево: если считать точки с одинаковыми координатами равными и учесть это в компараторе, то вставка нового значения в дерево не произойдёт.

Имеет смысл использовать коллекцию на основе бинарного дерева, так как элементы в открытый список добавляются не так часто, в то время как поиск минимального элемента по значению метрической функции выполняется на каждой итерации поискового алгоритма. Это связано с тем, что добавление в открытый список зависит от наличия аналогичного (по координатам) элемента в закрытом списке, который со временем растёт и в нём оказывается всё большее количество точек – чем больше точек в закрытом списке, тем меньше вероятность добавления элемента в открытый список. Но также хотелось бы иметь преимущества коллекции HashSet.

Я решил обобщить задачу. Пусть определена некоторая структура данных, в которой имеется набор полей. Пусть также некоторые поля определяют отношение эквивалентности двух элементов данной структуры, в то время как другие поля определяют отношения порядка (проще говоря, методы equals и hashCode используют одни поля объекта, а методы compare и compareTo другие).
Задача: реализовать структуру данных, в которой операция поиска элемента на основании равенства выполняется с асимптотикой O(1), а операции вставки и удаления работали с учётом операций и сравнения и равенства, и строили бинарное дерево таким образом, что наименьший элемент был бы корнем дерева.

Так как для моих целей мне нужно хранить в открытом списке точки с учётом их координат, то я могу однозначно определить хэш-функцию на основании размера карты проходимости так, что в ней будут отсутствовать коллизии, поэтому я и в коллекции решил задать константой максимальное количество элементов.



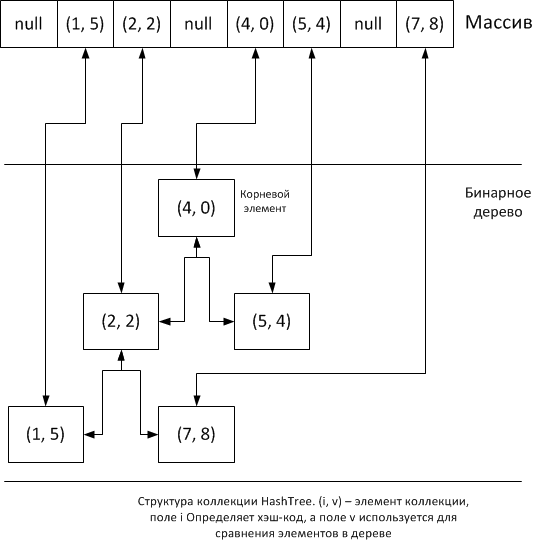
Идея очень проста: будем помещать на основании хеширования элементы коллекции в массив, и тут же помещать эти же элементы в бинарное дерево. Нам понадобиться внутренний класс для упаковки элементов в узлы дерева:

private static class Node<V extends Comparable<V>> {

        private Node parent;
        private Node left;
        private Node right;
        private int k = 0;
        private final V data;

        public Node(V data) {
            this.data = data;
            this.parent = null;
            this.left = null;
            this.right = null;
        }

    }

Тип V определяет элемент коллекции, он должен расширять класс Comparable, чтобы можно было выполнять сравнение для построения дерева.

В классе помимо указателей на левого и правого потомка есть указатель на предка. Это сделано для оптимизации процесса удаления элемента из дерева – имея прародителя удаляемого элемента можно исключить из алгоритма удаления обход дерева начиная с корня, для поиска можно будет воспользоваться массивом элементов. Поле с именем k содержит количество узлов поддерева, если они не представляют собой подряд идущие увеличивающиеся узлы по левому потомку.


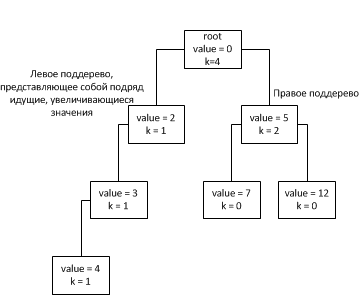
Внутри коллекции должен быть указатель на корень дерева и массив элементов коллекции, где в пустых ячейках хранится null, а в заполненных экземпляры класса Node, где в поле data будет храниться значение добавленного элемента (а точнее значение указателя на экземпляр объекта):

public abstract class HashTree<E extends Comparable<E>> {

    private Node root = null;
    private Node[] nodes;

    public HashTree(int capacity) {
        this.nodes = new Node[capacity];
    }

    public abstract int getElementHash(E element);
…
}

Как и тип V, тип E определяет элемент коллекции. По умолчанию коллекция пуста, поэтому указатель на корневой элемент – null и массив также заполнен значениями null. Класс абстрактный с абстрактным методом getElementHash, позволяющим переопределить вычисление хэш-кода.

Теперь к методам. Метод addElement:

public void addElement(E element) {
        	    int index = getElementHash(element);
        	    if (nodes[index] != null) {
            	        return;
        	    }
       	    Node<E> node = new Node<>(element);
        	    nodes[index] = node;
        	    this.root = connectNodes(this.root, node);
    	}

В методе получаем хэш-код добавляемого элемента. Создаём новый узел дерева с новым элементом в качестве данных и добавляем его в дерево и в массив, где хэш-код определяет индекс в массиве. Вставка элемента в массив имеет асимптотику O(1), вставка в дерево — O(log(n)), суммарная асимптотика – O(log(n)).

Метод removeElement:

public E removeElement(E element) {
        int index = getElementHash(element);
        Node node = nodes[index];
        if (node == null) {
            return null;
        }
        nodes[index] = null;
        E data = (E) node.data;
        Node l = getElemInArray(node.left);
        Node r = getElemInArray(node.right);
        if (l != null) {
            l.parent = null;
        }
        if (r != null) {
            r.parent = null;
        }
        l = connectNodes(l, r);
        if (node.parent == null) {
            this.root = l;
            if (this.root != null) {
                this.root.parent = null;
            }
            return data;
        }
        int p = getElementHash((E) node.parent.data);
        if (nodes[p] != null) {//здесь сравниваются ИМЕННО значение указателей, 
                               //интересует равенство адресов памяти, а не значений
            if (nodes[p].left == node) {
                nodes[p].left = null;
            }
            if (nodes[p].right == node) {
                nodes[p].right = null;
            }
        }
        connectNodes(nodes[p], l);
        return data;

    }

Здесь, используя хэш-код удаляемого элемента, извлекается из массива узел дерева, который нужно удалить. Используя предка удаляемого узла, выполняем удаление элемента, в процессе которого приходится 2 раза вызывать связывание поддеревьев, каждая из операций в худшем случае обладают асимптотикой – O(log(n)). В итоге метод имеет асимптотику O(log(n)).

Метод connectNodes выполняет присоединение, как одиночного узла, так и поддерева. Причём связывание происходит с применением сравнения. Таким образом, в вершине дерева всегда находится наименьший элемент.

Метод connectNodes:

private Node connectNodes(Node parent, Node node) {
        if (node == null) {
            return parent;
        }
        if (parent == null) {
            return node;
        } else {
            if (compare(node, parent) < 0) {
                return connectNodes(node, parent);
            }
            Node cur = parent;
            Node n = node;
            while (cur != null) {
                if (cur.left == null) {
                    cur.left = n;
                    n.parent = cur;
                    cur.k++;
                    break;
                }
                if (cur.right == null) {
                    if (compare(n, cur.left) <= 0) {
                        cur.right = cur.left;
                        cur.left = n;
                        n.parent = cur;
                        cur.k++;
                        break;
                    } else {
                        cur.right = n;
                        n.parent = cur;
                        cur.k++;
                        break;
                    }
                }
                if (compare(n, cur.left) <= 0) {
                    Node tmp = cur.left;
                    cur.left = n;
                    n.parent = cur;
                    cur.k++;
                    cur = n;
                    n = tmp;
                    continue;
                }
                if (compare(n, cur.right) < 0
                        && compare(n, cur.left) > 0) {
                    cur.k++;
                    if (cur.right.k < cur.left.k) {
                        Node tmp = cur.right;
                        cur.right = n;
                        n.parent = cur;
                        cur = n;
                        n = tmp;
                    } else {
                        cur = cur.left;
                    }
                    continue;
                }
                if (compare(n, cur.left) > 0) {
                    cur.k++;
                    cur = cur.left.k < cur.right.k ? cur.left : cur.right;
                }
            }
            return parent;
        }

Методу connectNodes стоит уделить особое внимание. Добавление нового элемента выполняется с использованием этого метода применительно к корню и новому элементу. Считаем, что дерево не пусто:


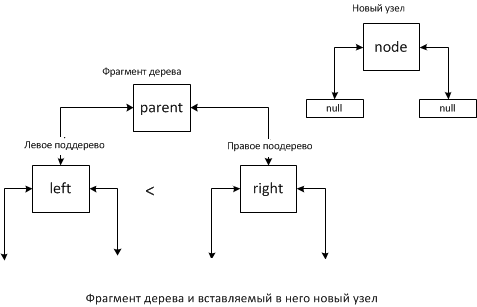
Возможно 4 случая:

1. новый элемент меньше корня;
2. новый элемент меньше левого потомка;
3. новый элемент больше левого потомка, но меньше правого;
4. новый элемент больше правого потомка.

Случай 1.
В данной ситуации левым потомком нового элемента становится parent, если parent — корень дерева, то соответственно новым корнем будет новый, добавленный элемент.


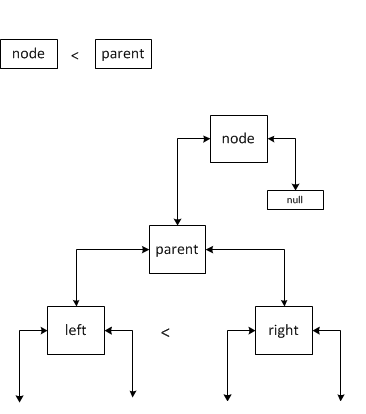
Случай 2.
Тут возможно два варианта: правый потомок определён и правый потомок не определен. Если левый потомок не определён, то мы считаем что левый потомок имеет большее значение новый узел. В обоих ситуациях новый элемент становится левым потомком parent, а left (который был левым потомком до добавления) становится правым потомком. Однако во втором случае нужно выполнить присоединение старого правого потомка right к новому правому потомку left. Присоединение left к right будет происходить по тем же правилам, что и в описываемых случаях.


Случай 3.
В этом случае выполняется либо переход по левому поддереву и добавление в него нового узла, если в нём меньше узлов чем в правом поддереве, либо заменяется правое поддерево right на вставляемый узел node и происходит добавление к нему правого поддерева right.


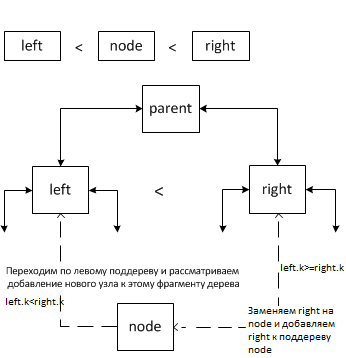
Случай 4.
В этом случае выполняется переход по тому поддереву, в котором меньше всего узлов. Число узлов накапливается в поле k.


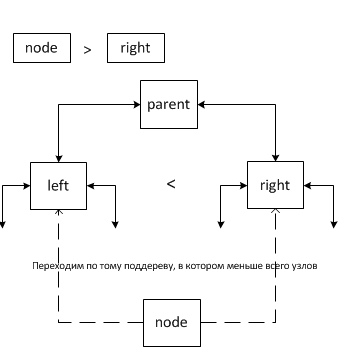
Теперь оценим асимптотику метода connectNodes. В лучшем случае, когда в дерево добавляются узлы без потомков в порядке уменьшения, асимптотика будет равна O(1), так как в этом случае поместить новый элемент на место прародителя. Если речь идёт о связывании узла с потомками и меньшим чем прародитель, то нужно будет пройти по поддереву узла. Для случая 2 в пункте а) асимптотика — O(1), а в пункте б) нужно вновь пройти по поддереву вставляемого узла.
Заметим, что поле k у узлов увеличивается для всех случаев, кроме 1-го, это сделано, чтобы дерево заполнялось симметрично, но не нарушая увеличивающегося порядка по левому поддереву если таковой встретится.

Чтобы оценить сложность прохода по дереву достаточно оценить его высоту. Высота дерева и будет искомой асимптотикой. Отдельным вопросом стоит наличие длиной последовательности по левому поддереву. Если учесть наличие таких поддеревьев, то в худшем случае асимптотику выполнения связывания можно считать как асимптотику связывания с поддеревом, которое мы хотим привязать, а в лучшем случае как O(1) (2 случай).


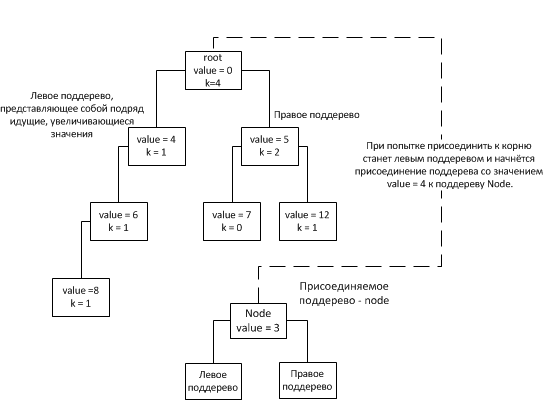
Так как при связывании узлов мы имеем дело с узлами внутри дерева значит высоту любого поддерева можно считать не превосходящей высоту самого дерева. Таким образом оценив высоту всего бинарного дерева получим асимптотику метода connectNodes. Из за того, что выбор поддерева для вставки выбирается на основании поля k узла (в котором хранится размер поддерева за исключением подряд идущих увеличивающихся узлов они считаются как один узел), дерево стремится заполнить следующий свой уровень только после заполнения предыдущего (исключая, конечно же описанный выше случай 1). Таким образом древо будет иметь вид:


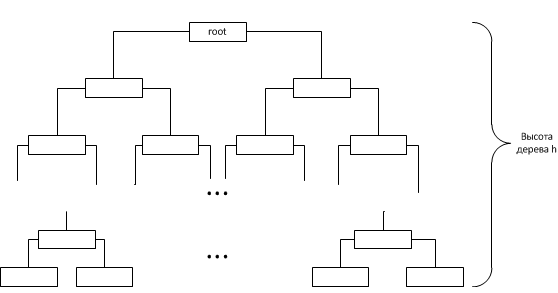
Таким образом, если n — количество узлов в дереве, то $$. Из чего вытекает, что высота дерева $$. Отсюда следует, что асимптотика метода connectNodes — O(log(n)).

Поиск элемента можно осуществлять не в дереве, а в массиве на основании хэш-кода, поэтому операция поиска имеет асимптотику O(1). А так как дерево организовано как бинарное, то в корне всегда находится минимальный элемент по сравнению и асимптотика поиска минимального — O(1). Замечу, что удаление минимального элемента имеет асимптотику O(log(n)), так как при удалении требуется реорганизовать дерево, начиная с корня применяя метод connectNodes.

На первый взгляд операция удаления минимального элемента в реализованной коллекции имеет худшую асимптотику, чем у коллекции HashSet, но не стоит забывать, что прежде чем удалить минимальный элемент его сначала нужно найти, а для этого требуется выполнить операции с асимптотикой O(n). Таким образом, итоговая асимптотика операции удаления минимального элемента в коллекции HashSet будет иметь вид – O(n).

Проверка наличия элемента в коллекции, как уже говорилось выше, выполняется на основании проверки на null элемента массива по индексу, определяемому хэш-кодом элемента. Проверка выполняется методом contains и имеет асимптотику O(1):

public boolean contains(E element) {
        int index = getElementHash(element);
        return nodes[index] != null;
 } 

Также на основании хэш-кода выполняется поиск по равенству при чём с той же асимптотикой при помощи метода getElement:

public E getElement(E element) {
        return (E) nodes[getElementHash(element)].data;
 }

Реализованная коллекция не лишена недостатков. Она требует больше памяти, ей нужна хэш-функция без коллизий и для реализации перебора элементов придётся реализовывать обход дерева, что также не доставляет удовольствия, но данная коллекция предназначена для других целей. Главное преимущество – это возможность поиска элементов одного типа по разным критериям с наилучшей асимптотикой. В применении к моей задаче, это был поиск по равенству на основании координат и поиск минимального элемента на основании сравнения значений метрической функции.

В конце приведу результаты тестирования коллекции на быстродействие по сравнению с коллекциями LinkedHashMap, TreeSet и HashSet. Все коллекции заполнялись 1000 значений типа Integer и, с заполненными коллекциями, проводился следующий набор операций:

1. помещение нового элемента в коллекцию;
2. проверка на наличие в коллекции элемента с заданным значением (проверка выполнялась дважды для элемента, который был в коллекции и для элемента, которого в коллекции не было);
3. поиск и удаление минимально по сравнения элемента;
4. удаление, добавленного в пункте 1, элемента.

Результаты тестов приведены в таблице:

Коллекция	Количество повторений	Затраченное время
LinkedHashMap	10 000 000	1985±90 мс
TreeSet	10 000 000	1190±25 мс
HashSet	1 000 000	4350±100 мс
HashTree	10 000 000	935±25 мс

В итоге имеем более чем в 2 раза большую скорость коллекции HashTree по сравнению с LinkedHashMap и в 1.27 раза большую по сравнению с TreeSet (рассматривать HashSet не имеет смысла вообще). Проверки выполнялись на машине с 4Гб оперативной памяти и процессором AMD Phenom(tm)II X4 940, ОС – 32-разрядная Windows7 Профессиональная.