Введение
В публикациях [1,2,3,4] были рассмотрены отдельные элементы САУ и АСР, поэтому целесообразно рассмотреть решение задач анализа и синтеза таких систем в целом. Рассмотрим простую модель поверхностного водо-водяного теплообменника [5].
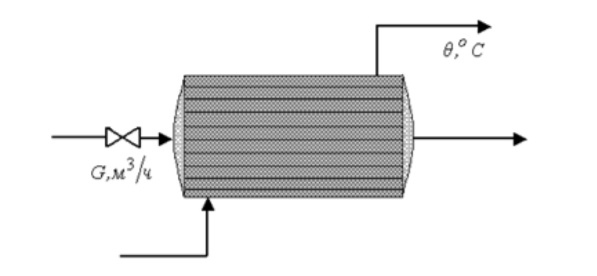
Постановка задачи
Проведём анализ и синтез АСР, используя её структурную схему, приведенную на рисунке:

На рисунке используются следующие обозначения:
Y(s)– изображение регулируемой величины y(t);
U(s) – изображение сигнала задания u (t);
E(s) – изображение ошибки регулирования ?(t)=u(t)-y(t);
M(s) – изображение регулирующего параметра µ(t);
?(s)– изображение возмущения по каналу регулирующего органа ?(t);
X(s)– изображение входной переменной объекта регулирования x(t)= µ(t)+ ?(t);
Wp (s) – передаточная функция регулятора;
Wоб (s) – передаточная функция объекта регулирования.
Одноконтурная АCР работает по принципу отклонений. На вход автоматического регулятора поступает два сигнала: сигнал задания u(t) и регулируемый параметр y(t). На основании ошибки регулирования ?(t)=u(t)-y(t), регулятор вырабатывает регулирующее воздействие µ(t) таким образом, чтобы минимизировать ошибку регулирования ?(?) – 0.
Для приведенной структурной схемы необходимо решить следующие задачи:
- Построить структурную схему АСР.
- Сделать декомпозицию математической модели теплообменника, представив её в виде соединения трех последовательно соединенных А- звеньев. Получить аналитическое выражение передаточной функции объекта регулирования.
- Рассчитать и построить кривую разгона для максимального возмущения по расходу греющей воды. На график нанести линию допустимого отклонения температуры нагреваемой воды.
- Рассчитать и построить в плоскости параметров ПИ-регулятора Ki=Кр /T1 и Кр график линии заданного запаса устойчивости анализируемой системы регулирования (m= mзд). Здесь же рассчитать и построить линию границы устойчивой работы системы (m=0).
- Определить из полученного в п.4. графика оптимальные параметры настройки ПИ-, П- и И- регуляторов и отметить их на плоскости настроечных параметров.
- Рассчитать и построить для одноконтурной АCР с ПИ-, П- и И- регуляторами переходные процессы для максимального возмущения по расходу греющей воды.
- Провести анализ переходных процессов.
- Рассчитать и построить КЧХ (комплексную частотную характеристику):
— для объекта регулирования;
— для замкнутой АCР с П-, И- и ПИ-регуляторами. - Построить график АЧХ замкнутой системы с ПИ-регулятором и определить значение частотного показателя колебательности.
- Сделать выводы о результатах расчетов (соответствие фактических и допустимых отклонений температуры). Дать рекомендации.
- Составить упрощенную функциональную схему АСР температуры нагреваемой воды теплообменника ?(t).
Декомпозиция модели теплообменника
В соответствии с исходными данными, математическая модель теплообменника представлена в виде линейного дифференциального уравнения с постоянными коэффициентами:

Преобразовав по Лапласу левую и правую части уравнения (1), получим аналитическое выражение передаточной функции объекта регулирования:

Декомпозиция модели теплообменника состоит в разбиении сложной передаточной функции (2) на комбинацию простых передаточных функций элементарных динамических звеньев. Представим передаточную функцию объекта регулирования в виде последовательного соединения трех апериодических звеньев (А-звеньев):

Сравнив выражения (2) и (3), можно определить коэффициенты передачи звеньев:

Для определения постоянных времени звеньев T1, T2 и T3, необходимо разложить на множители характеристическое уравнение объекта (знаменатель передаточной функции (2)).
Для этого найдем его корни. Для определения корней характеристического уравнения, будем использовать модуль SymPy.
В пакете есть функция real_roots (), которая возвращает только вещественные корни.
Программа Python
# -*- coding: utf8 -*-
import numpy as np
import matplotlib.pyplot as plt
from sympy import *
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
x=S('x')
p = 80*x**3+56*x**2+13*x+1
z=real_roots(p)# Символьное решение уравнения для постоянных времени звеньев
print('Уравнение -%s имеет корни : %s, %s,%s'%(p, z[2], z[1],z[0]))
Получим:
Уравнение -80*x**3 + 56*x**2 + 13*x + 1 имеет корни: -1/5, -1/4,-1/4
Зная корни характеристического уравнения, найдем постоянные времени А-звеньев:
Программа Python
T1=-1/z[2];T2=-1/z[1];T3=-1/z[0]
print («Постоянные времени звеньев: A1 — %s, A2- %s, A3-%s»% ( T1,T2,T3))
Получим:
Постоянные времени звеньев: A1 — 5, A2- 4, A3-4
Построение кривой разгона объекта регулирования методом имитационного моделирования на основе разностных уравнений
Кривой разгона называется реакция динамической системы на ступенчатое воздействие произвольной амплитуды. Применительно к теплообменнику, кривой разгона будет называться изменение температуры нагреваемого теплоносителя ?(t) при ступенчатом изменении входного воздействия G(t).
Согласно заданию, величина отклонения входного воздействия равна 9% относительно установившегося статического значения. Построение кривой разгона будем осуществлять путем численного решения дифференциальных уравнений А-звеньев методом Эйлера. Введем исходные значения и параметры для моделирования.
Расчет кривой разгона осуществляет подпрограмма KR. Следует отметить, что начальным значением входного воздействия является максимальное отклонение расхода греющего теплоносителя Gmax относительно установившегося статического значения.
Программа Python
# -*- coding: utf8 -*-
import numpy as np
import matplotlib.pyplot as plt
from sympy import *
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
x=S('x')
p = 80*x**3+56*x**2+13*x+1
z=real_roots(p)# Символьное решение уравнения для постоянных времени звеньев
print('Уравнение -%s имеет корни : %s, %s,%s'%(p, z[2], z[1],z[0]))
T1=-1/z[2];T2=-1/z[1];T3=-1/z[0]
print("Постоянные времени звеньев: A1 - %s, A2- %s, A3-%s"%(T1,T2,T3))
K1= 1.5; K2= 1; K3= 1# коэффициенты усиления звеньев
dt= 0.01 #Шаг моделирования
N =10000 #Число точек кривой разгона
?st = 84.97 #Статическое значение температуры нагреваемой воды
Gst = 470.1#Статическое значение расхода греющей воды
Gmax =0.02* Gst #Максимальное отклонение расхода ?
?dop =0.09* ?st #Допустимое отклонение температуры:
x=[0 for w in np.arange(0,N)]# начальное заполнение списка x
y1=[0 for w in np.arange(0,N)]#начальное заполнение списка y1
y2=[0 for w in np.arange(0,N)]#начальное заполнение списка y2
y3=[0 for w in np.arange(0,N)]#начальное заполнение списка y3
x[0]=Gmax
def f(K,T,dt,x,y):# Разностное уравнение для звеньев А
return (1-dt/T)*y+K*x*(dt/T)
for i in np.arange(0,N):# Решение разностопного уравнения звеньев А
if i+1>N-1:break
y1[i+1]=f(K1,T1,dt,x[0],y1[i])
y2[i+1]=f(K2,T2,dt,y1[i+1],y2[i])
y3[i+1]=f(K3,T3,dt,y2[i+1],y3[i])
v=[w+?st for w in y3]# список для КР
t=[dt*i for i in np.arange(0,N)]# список для времени
u=[?st+?dop for i in np.arange(0,N)]# список для допуска на температуру
plt.title('Построение кривой разгона объекта регулирования ') #Заголовок
plt.ylabel('Температура теплоносителя') #Метка по оси y
plt.xlabel('Время - t') #Метка по оси x
plt.grid(True) #Сетка
plt.plot(t,v,"--r",linewidth=2,label='Кривая разгона объекта регулирования') #Построение графика
plt.plot(t,u,"b",linewidth=2,label='Допустимое отклонение температуры') #Построение графика
plt.legend(loc='best')
plt.show() #Показать графикПолучим:
Уравнение -80*x**3 + 56*x**2 + 13*x + 1 имеет корни: -1/5, -1/4,-1/4
Постоянные времени звеньев: A1 — 5, A2- 4, A3-4

Как видно из полученного графика, при изменении расхода греющего теплоносителя на 9%, температура нагреваемого теплоносителя увеличивается и превышает предельно допустимое отклонение.
Для предотвращения этого, необходимо спроектировать автоматическую систему регулирования. Проектирование АСР заключается в выборе регуляторов различной структуры, их настройке и анализе. Проанализируем работу АСР с П-, И- и ПИ-регуляторами.
Построение линии границы устойчивости и линии заданного запаса устойчивости в плоскости настроечных параметров ПИ-регулятора
Для расчета оптимальных параметров П-, И-, ПИ- регуляторов будем использовать метод настройки при ограничении на корневой показатель колебательности m.
Для этого необходимо в плоскости настроечных параметров ПИ- регулятора [Kp, Ki] построить линию заданного запаса устойчивости m.
Координаты максимума этой кривой будут являться оптимальными настроечными параметрами ПИ-регулятора, точка с координатами [Kp,0] – оптимальными настроечными параметрами П-регулятора, а точка с координатами [0, Ki] — оптимальными настроечными параметрами И- регулятора.
Построим в плоскости настроечных параметров ПИ-регулятора линии границы устойчивости (m=0; = 0) и заданного запаса устойчивости (m=0.351; = 0.89):
Программа Python
#!/usr/bin/env python
#coding=utf8
import matplotlib.pyplot as plt
import numpy as np
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
def f(w,m):
T1=5;T2=4;T3=4
K1=1.5; K2=1;K3=1
j=(-1)**0.5
return K1/(T1*w*(j-m)+1)*K2/(T2*w*(j-m)+1)*K3/(T3*w*(j-m)+1)
Kp=[-(0.351* f(w,0.351).imag +f(w,0.351).real)/((f(w,0.351).imag)**2+(f(w,0.351).real)**2) for w in np.arange(0,5,0.001)]
Ki=[-((0.351**2+1)*w* f(w,0.351).imag)/((f(w,0.351).imag)**2+(f(w,0.351).real)**2) for w in np.arange(0,5,0.001)]
plt.title('Плоскость настроечных параметров ПИ-регулятора ')
plt.ylabel('Ki(0.351,w), Ki(0,w)')
plt.xlabel('Kp(0.351,w), Kp(0,w)')
plt.axis([0.0, 6.0, 0.0, 0.4])
plt.plot(Kp, Ki, color='r',linewidth=2, label='Линия заданного запаса устойчивости ')
Kp0=[-(0.0* f(w,0.0).imag +f(w,0.0).real)/((f(w,0.0).imag)**2+(f(w,0.0).real)**2) for w in np.arange(0,5,0.001)]
Ki0=[-((0.0+1)*w* f(w,0.0).imag)/((f(w,0.0).imag)**2+(f(w,0.0).real)**2) for w in np.arange(0,5,0.001)]
plt.plot(Kp0, Ki0, color='b',linewidth=2, label='Линия границы устойчивости')
plt.legend(loc='best')
plt.grid(True)
plt.show()
Получим:

Определим оптимальные параметры настройки П-, И- и ПИ-регуляторов, а также параметры ПИ-регулятора на границе устойчивости по ранее приведенным условиям:

Расчет переходных процессов в АСР методом имитационного моделирования
Для расчета переходных процессов в замкнутой АСР методом имитационного моделирования, необходимо дополнительно к ранее записанному разностному уравнению А-звена дописать разностные уравнения для П- и И-звеньев.
Программа Python
# -*- coding: utf8 -*-
import numpy as np
import matplotlib.pyplot as plt
from sympy import *
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
T1=5;T2=4;T3=4#постооянные времени звеньев
K1= 1.5; K2= 1; K3= 1# коэффициенты усиления звеньев
dt= 0.01 #Шаг моделирования
N =10000 #Число точек кривой разгона
?st = 84.97 #Статическое значение температуры нагреваемой воды
Gst = 470.1#Статическое значение расхода греющей воды
Gmax =0.02* Gst #Максимальное отклонение расхода
?dop =0.09* ?st #Допустимое отклонение температуры:
x=[0 for w in np.arange(0,N)]# начальное заполнение списка x
y1=[0 for w in np.arange(0,N)]#начальное заполнение списка y1
y2=[0 for w in np.arange(0,N)]#начальное заполнение списка y2
y3=[0 for w in np.arange(0,N)]#начальное заполнение списка y3
mu=[0 for w in np.arange(0,N)]#начальное заполнение списка mu
ep=[0 for w in np.arange(0,N)]#начальное заполнение списка ep
ii=[0 for w in np.arange(0,N)]#начальное заполнение списка ii
"""Переходные процессы в АСР при ступенчатом возмущении Gmax
по каналу регулирующего воздействия"""
def PP(Kp,Ki):
def fa(K,T,dt,x,y):#Разностное уравнение кривой разгона
return (1-dt/T)*y+K*x*(dt/T)
def fi(K,dt,x,y):
return dt*K*x+y#Разностное уравнение И-звена
def fp(K,x):
return K*x#Разностное уравнение П-звена
for i in np.arange(0,N):# численное решение разностных уравнений
if i+1>N-1:break
x[i+1]=mu[i]+Gmax
y1[i+1]=fa(K1,T1,dt,x[i],y1[i])
y2[i+1]=fa(K2,T2,dt,y1[i],y2[i])
y3[i+1]=fa(K3,T3,dt,y2[i],y3[i])
ep[i+1]=-y3[i]
ii[i+1]=fi(Ki,dt,ep[i],ii[i])
mu[i+1]= fp(Kp,ep[i])+ii[i+1]
return y3
""" Оптимальные настройки регуляторов"""
KpП= 1.299; KiП= 0
KpИ= 0; KiИ= 0.053
KpПИ = 0.734; KiПИ = 0.105
Kpгр = 2.366; Kiгр = 0.352
""" Учёт ?st """
VПИ=[w+?st for w in PP(KpПИ,KiПИ)]
VП=[w+?st for w in PP(KpП,KiП)]
VИ=[w+?st for w in PP(KpИ,KiИ)]
Vгр=[w+?st for w in PP(Kpгр,Kiгр)]
V=[w+?st for w in PP(0,0)]
u=[?st+?dop for i in np.arange(0,N)]
t=[dt*i for i in np.arange(0,N)]
plt.title('Переходные процессы в АСР при ступенчатом возмущении ')
plt.ylabel('VПИ,VП,VИ,Vгр,u') #Метка по оси y
plt.xlabel('Время - t') #Метка по оси x
plt.grid(True) #Сетка
plt.plot(t,VП,linewidth=2,label='АСР с П-регулятором')
plt.plot(t,VИ,linewidth=2,label='АСР с И-регулятором')
plt.plot(t,VПИ,linewidth=2,label='АСР с ПИ-регулятором')
plt.plot(t,Vгр,linewidth=2,label='АСР на границе устойчивости')
plt.plot(t,u,linewidth=2,label='Допустимое отклонение температуры')
plt.plot(t,V,linewidth=2,label='Кривая разгона объекта регулирования ')
plt.legend(loc='best')
plt.show() #Показать график
Получим:


Функция PP(Kp,Ki) рассчитывает отклонение температуры теплоносителя от некоторого установившегося значения при изменении расхода греющей жидкости Gmax.
В качестве аргументов функции PP (Kp, Ki), необходимо подставить ранее рассчитанные настроечные параметры П-, И- и ПИ-регуляторов Kp и Ki.
Для построения графиков изменения температуры нагреваемой воды ?(t), необходимо рассчитанное отклонение прибавить к её статическому значению ?st.
Расчет КЧХ объекта регулирования и замкнутой АСР
Введем последовательно формулы, вычисляющие КЧХ объекта регулирования, регулятора и замкнутой АСР. Для вычисления вещественной и мнимой составляющих комплексных частотных характеристик, необходимо использовать встроенные функции Python image и real.
Построим графики КЧХ объекта регулирования и замкнутой АСР с П-, И- и ПИ-регуляторами, подставляя в качестве аргументов функции fz(Kp,Ki), посчитанные ранее настроечные параметры регуляторов.
Программа Python
#!/usr/bin/env python
#coding=utf8
import matplotlib.pyplot as plt
import numpy as np
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
def f(w):#КЧХ объекта регулирования
T1=5;T2=4;T3=4
K1=1.5; K2=1;K3=1
j=(-1)**0.5
return K1/(T1*w*j+1)*K2/(T2*w*j+1)*K3/(T3*w*j+1)
""" Вещественная (Re) и мнимая (Im) части КЧХ объекта регулирования """
Im=[f(w).imag for w in np.arange(0.001,5,0.001)]
Re=[f(w).real for w in np.arange(0.001,5,0.001)]
def fz(Kp,Ki):
j=(-1)**0.5
"""Вещественная (Rez) и мнимая (Imz) части КЧХ замкнутой АСР """
Imz=[(((Kp*j*w+Ki)*f(w))/(j*w+(Kp*j*w+Ki)*f(w))).imag for w in np.arange(0.001,5,0.001)]
Rez=[(((Kp*j*w+Ki)*f(w))/(j*w+(Kp*j*w+Ki)*f(w))).real for w in np.arange(0.001,5,0.001)]
return Rez,Imz
KpП= 1.299; KiП= 0
KpИ= 0; KiИ= 0.053
KpПИ = 0.734; KiПИ = 0.105
plt.title('Графики КЧХ ')
plt.ylabel('Im(w),Imz(KpПИ,KiПИ),Imz(KpП,KiП),Imz(KpИ,KiИ)')
plt.xlabel('Re(w),Rez(KpПИ,KiПИ),Rez(KpП,KiП),Rez(KpИ,KiИ)')
plt.axis([-1.0, 2.0, -2.0, 0.5])
plt.plot(Re,Im,linewidth=2, label='КЧХ объекта регулирования ')
Rez,Imz=fz(KpПИ,KiПИ)
plt.plot(Rez,Imz ,linewidth=2, label='КЧХ замкнутой АСР с ПИ-регулятором')
Rez,Imz=fz(KpП,KiП)
plt.plot(Rez,Imz ,linewidth=2, label='КЧХ замкнутой АСР с П-регулятором')
Rez,Imz=fz(KpИ,KiИ)
plt.plot(Rez,Imz ,linewidth=2, label='КЧХ замкнутой АСР с И-регулятором')
plt.legend(loc='best')
plt.grid(True)
plt.show()
Получим:

Необходимо обратить внимание, что график КЧХ объекта регулирования начинается на действительной оси при частоте w=0 и приходит в начало координат при частоте w=?.
Причем, Re(0)=1.5, что совпадает с коэффициентом усиления объекта.
Графики КЧХ замкнутой АСР с ПИ- и И-регулятором выходят из точки [1, j?0] при w=0, что говорит о соблюдении точности регулирования в установившемся режиме y(?)=u(?).
График КЧХ замкнутой АСР с П-регулятором при w= 0 выходит из точки, координаты которой можно посчитать исходя из выражения:

Это означает, что при единичном ступенчатом возмущении по каналу задания U(s), АСР с П-регулятором будет обладать остаточной неравномерностью 0.66 0C, y (?) = 0.66 • u (?).
Расчет АЧХ замкнутой АСР с ПИ-регулятором
Программа Python
#!/usr/bin/env python
#coding=utf8
import matplotlib.pyplot as plt
import numpy as np
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
def f(w):
T1=5;T2=4;T3=4
K1=1.5; K2=1;K3=1
j=(-1)**0.5
return K1/(T1*w*j+1)*K2/(T2*w*j+1)*K3/(T3*w*j+1)
Im=[f(w).imag for w in np.arange(0.001,5,0.001)]
Re=[f(w).real for w in np.arange(0.001,5,0.001)]
def fz(Kp,Ki):
j=(-1)**0.5
Modz=[abs(((Kp*j*w+Ki)*f(w))/(j*w+(Kp*j*w+Ki)*f(w))) for w in np.arange(0.001,1,0.001)]
return Modz
KpПИ = 0.734; KiПИ = 0.105
plt.title('Расчет АЧХ замкнутой АСР с ПИ-регулятором ')
plt.ylabel('A(w,KpПИ,KiПИ)')
plt.xlabel('Частота -w')
w=np.arange(0.001,1,0.001)
Modz=fz(KpПИ,KiПИ)
Amax=max(Modz)
Wmax=Modz.index(Amax)
print('Значение АЧХ - %s на резонансной частоте -%s'%(round(Amax,3),w[Wmax]))
print('Значение частотного показателя колебательности -%s'%round(Amax/Modz[0],3))
plt.plot(w,Modz ,'r',linewidth=2, label='АЧХ ')
plt.legend(loc='best')
plt.grid(True)
plt.show()
Получим:
Значение АЧХ — 1.454 на резонансной частоте -0.156
Значение частотного показателя колебательности -1.454

Оценка качества и анализ переходных процессов
Для оценки качества переходных процессов на практике обычно используются прямые и косвенные показатели. Прямые показатели качества определяются непосредственно по виду переходного процесса. К ним относятся: динамическая ошибка yдин, время регулирования tр, степень затухания, перерегулирование и т.п.
Значения косвенных показателей не позволяют напрямую оценить характер переходных процессов, однако они широко используются для сравнения качества регулирования различных систем между собой.
Для оценки качества регулирования АСР с П-, И- и ПИ-регуляторами будем использовать в качестве прямых показателей качества степень затухания и динамическую ошибку регулирования yдин, а в качестве косвенных показателей – линейный интегральный критерий и интегральный критерий по модулю. Ниже приведена программа для расчета показателей качества регулирования.
Программа Python
# -*- coding: utf8 -*-
import numpy as np
import matplotlib.pyplot as plt
from sympy import *
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
T1=5;T2=4;T3=4#постооянные времени звеньев
K1= 1.5; K2= 1; K3= 1# коэффициенты усиления звеньев
dt= 0.01 #Шаг моделирования
N =10000 #Число точек кривой разгона
?st = 84.97 #Статическое значение температуры нагреваемой воды
Gst = 470.1#Статическое значение расхода греющей воды
Gmax =0.02* Gst #Максимальное отклонение расхода ?
?dop =0.09* ?st #Допустимое отклонение температуры:
x=[0 for w in np.arange(0,N)]# начальное заполнение списка x
y1=[0 for w in np.arange(0,N)]#начальное заполнение списка y1
y2=[0 for w in np.arange(0,N)]#начальное заполнение списка y2
y3=[0 for w in np.arange(0,N)]#начальное заполнение списка y3
mu=[0 for w in np.arange(0,N)]#начальное заполнение списка mu
ep=[0 for w in np.arange(0,N)]#начальное заполнение списка ep
ii=[0 for w in np.arange(0,N)]#начальное заполнение списка ii
"""Переходные процессы в АСР при ступенчатом возмущении Gmax
по каналу регулирующего воздействия"""
def PP(Kp,Ki):
def fa(K,T,dt,x,y):#Разностное уравнение кривой разгона
return (1-dt/T)*y+K*x*(dt/T)
def fi(K,dt,x,y):
return dt*K*x+y#Разностное уравнение И-звена
def fp(K,x):
return K*x#Разностное уравнение П-звена
for i in np.arange(0,N):# численное решение разностных уравнений
if i+1>N-1:break
x[i+1]=mu[i]+Gmax
y1[i+1]=fa(K1,T1,dt,x[i],y1[i])
y2[i+1]=fa(K2,T2,dt,y1[i],y2[i])
y3[i+1]=fa(K3,T3,dt,y2[i],y3[i])
ep[i+1]=-y3[i]
ii[i+1]=fi(Ki,dt,ep[i],ii[i])
mu[i+1]= fp(Kp,ep[i])+ii[i+1]
return y3
""" Оптимальные настройки регуляторов"""
KpП= 1.299; KiП= 0
KpИ= 0; KiИ= 0.053
KpПИ = 0.734; KiПИ = 0.105
Kpгр = 2.366; Kiгр = 0.352
""" Учёт ?st """
VПИ=[w+?st for w in PP(KpПИ,KiПИ)]
print("АСР с ПИ-регулятором")
Dуст=round((VПИ[N-1]),3)
print("Установившееся значение температуры -%s"%Dуст)
D1=round(max(VПИ),3)
print(" Первая амплитуда переходного процесса A1 минус t установ.-%s"%D1)
D2=round((VПИ[6400-1]),3)
print(" Третья амплитуда переходного процесса A3 минус t установ.-%s"%D2)
D=(D1-D2)/(D1-Dуст)
print(" Степень затухания-%s "%(round(D,3)))
VПии=sum([dt*w for w in PP(KpПИ,KiПИ)])
print("Интегральный критерий -%s"%round((VПии),3))
VПии=sum([abs(dt*w) for w in PP(KpПИ,KiПИ)])
print('Интеграл по модулю -%s'%round((VПии),3))
VП=[w+?st for w in PP(KpП,KiП)]
print("АСР с П-регулятором")
Dуст=round((VП[N-1]),3)
print("Установившееся значение температуры -%s"%Dуст)
D1=round(max(VП),3)
print(" Первая амплитуда переходного процесса A1 минус t установ.-%s"%D1)
D2=round((VП[6940-1]),3)
print(" Третья амплитуда переходного процесса A3 минус t установ.-%s"%D2)
D=(D1-D2)/(D1-Dуст)
print(" Степень затухания--%s "%(round(D,3)))
VПии=sum([dt*w for w in PP(KpП,KiП)])
print("Интегральный критерий --%s"%round((VПии),3))
VПи=sum([abs(dt*w) for w in PP(KpП,KiП)])
print('Интеграл по модулю -%s'%round((VПи),3))
VИ=[w+?st for w in PP(KpИ,KiИ)]
print("АСР с И-регулятором")
Dуст=round((VИ[N-1]),3)
print("Установившееся значение температуры -%s"%Dуст)
D1=round(max(VИ),3)
print(" Первая амплитуда переходного процесса A1 минус t установ.-%s"%D1)
D2=round((VИ[9940-1]),3)
print(" Третья амплитуда переходного процесса A3 минус t установ.-%s"%D2)
D=(D1-D2)/(D1-Dуст)
print(" Степень затухания--%s "%(round(D,3)))
VПии=sum([dt*w for w in PP(KpИ,KiИ)])
print("Интегральный критерий --%s"%round((VПии),3))
VПи=sum([abs(dt*w) for w in PP(KpИ,KiИ)])
print('Интеграл по модулю -%s'%round((VПи),3))
Получим:
АСР с ПИ-регулятором
Установившееся значение температуры -84.976
Первая амплитуда переходного процесса A1 минус t установ.-91.609
Третья амплитуда переходного процесса A3 минус t установ.-84.987
Степень затухания-0.998
Интегральный критерий -89.707
Интеграл по модулю -123.746
АСР с П-регулятором
Установившееся значение температуры -89.753
Первая амплитуда переходного процесса A1 минус t установ.-91.15
Третья амплитуда переходного процесса A3 минус t установ.-89.762
Степень затухания--0.994
Интегральный критерий --457.272
Интеграл по модулю -457.272
АСР с И-регулятором
Установившееся значение температуры -85.848
Первая амплитуда переходного процесса A1 минус t установ. -95.087
Третья амплитуда переходного процесса A3 минус t установ.-85.883
Степень затухания--0.996
Интегральный критерий --178.211
Интеграл по модулю -329.97
Выводы:
Оценка степени затухания переходных процессов практически совпадает с заданной, что говорит о высокой точности моделирования АСР;
АСР с И-регулятором обладает наибольшей динамической ошибкой регулирования и затянутым по времени переходным процессом. Кроме того, величина динамической ошибки превышает предельно допустимое значение, поэтому использование И-регулятора по техническим условиям задачи становится невозможным;
АСР с П-регулятором обладает наименьшей динамической ошибкой регулирования, однако для него наблюдается эффект остаточной неравномерности. Установившееся значение температуры на выходе из теплообменника не совпадает с её статическим значением, что и подтверждается завышенными значениями интегральных критериев. Исходя из этого, П-регулятор нельзя рекомендовать к использованию для регулирования температуры теплообменника;
Наилучшими интегральными показателями качества регулирования обладает АСР с ПИ-регулятором. С учетом того, что максимальное отклонение температуры для АСР с ПИ-регулятором не превышает предельно допустимого значения, ПИ-регулятор является наиболее
предпочтительным для регулирования температуры теплообменника.


Karroplan
У вас совсем не используется ни одна методика программирования для именно анализа или моделирования. Вы заранее аналитическим методом упростили систему до уравнения простейшего вида и используете минимальные средства программирования и вообще никакие средства самого питона. Такую «программу» можно было написать на любом императивном языке и она отличалась бы только косметически.
Если бы вы изначально в виде классов или допустим функций описали бы атомарные компоненты системы и использовали бы какие-то средства композиции из этих классов или средства функционального программирования для «собирания» системы из элементарных функций и потом применили бы какие-то именно библиотеки питона для решения таких уравнений или сами бы их написали — вот тогда можно было бы сказать, что «анализ на питоне».
а так — фуфел какой-то