Чем мы, физики, не занимаемся (по крайней мере никто из моих знакомых не утверждал, что занимается этим), так это не представляем себе дополнительные измерения. Мой мозг ограничен точно так же, как ваш, и хотя этот мозг легко создаёт трёхмерное изображение мира, в котором я могу двигаться, я не могу заставить его представить изображение четырёх- или пятимерного мира, как и вы. Моё выживание не зависело от возможности представлять что-либо подобное, так что, возможно, и неудивительно, что мой мозг на это не настроен.
Я вместо этого (и, судя по нашему обмену идеями, большая часть моих коллег тоже) разрабатываю интуицию на основе комбинации из аналогий, трюков с визуализацией и расчётов. Расчёты мы здесь опустим, но многие аналогии и трюки не так уж сложно объяснить.
Размышлениям о дополнительных измерениях можно научиться в два этапа.
- Простой этап — научиться представлять или описывать мир с дополнительными измерениями. Вам уже известно несколько способов для этого, даже если вы это и не осознаёте — и вы можете выучить ещё немного.
- Этап посложнее — научиться тому, как в мире с дополнительными измерениями всё работает. Как работать иглой в четырёх измерениях, а не в трёх; будут ли планеты двигаться по орбитам вокруг Солнца в шести пространственных измерениях; сформируются ли протоны и атомы? Тут вам нужно будет узнать незнакомые трюки, представляя различия между миром с только одним или двумя измерениями и трёхмерным, известным нам, миром, и работая по аналогии.
Так что начнём с того, что поможем вам представлять мир с дополнительными измерениями. Для этого нужно подумать о том, как вообще мы представляем любое измерение. Начнём с начала.
- Мир с нулём измерений — это точка. О нём сейчас мало что можно сказать, но мы к нему вернёмся.
- Одномерный мир уже довольно интересен.
- В двумерных мирах происходит гораздо больше интересного.
- Важно избежать путаницы между пространственными измерениями и более общего смысла слова «измерение» в обычном языке, а также в математике и статистике.
- И дальше последуют различные примеры дополнительных измерений, с упором на то, что именно значит «дополнительные», и как может быть, что в нашем мире существуют измерения, о которых мы ничего не знаем.
- Также мы рассмотрим, как именно можно обнаружить эти незаметные измерения.
Одномерные миры
Мир с одним пространственным измерением гораздо проще мира с тремя, но и в нём есть кое-что, о чём можно порассуждать. К примеру, существуют несколько видов одномерных миров. У них есть не только определённые общие свойства, но и интересные различия.
Для первого примера давайте рассмотрим измерение не как физическое, а как более общее понятие. Это поможет вам во многих смыслах, например, отвлечёт вашу интуицию от естественных заблуждений по поводу того, что такое измерения и как они работают. Давайте поговорим о годовом заработке — сколько денег получает человек за определённый год. Это такое же подходящее для изучения измерение, как и все остальные.
Доходное измерение
Ваш доход за прошлый год — это определённое число в вашей местной валюте. Он может быть положительным или отрицательным, большим или маленьким; его можно представить как точку на линии, как на рис. 1, которую мы будем называть «точкой дохода». Каждая точка на линии представляет возможный доход.
Рис. 1: доходная линия бесконечной длины, левая часть которой представляет убытки, правая — доходы.
Что делает годовой доход одномерным свойством, так это (очень грубо говоря) следующее:
• Положение в пространстве обозначается одой единицей информации: в нашем случае, доходом.
Также заметьте, что он непрерывен (или практически непрерывен) — если у двух людей разные доходы А и В, мы можем найти третьего, чей доход находится между А и В.
Два этих факта подразумевают, что доход может меняться непрерывно по доходной линии, перемещаясь вправо или влево — либо к более высокому, либо к более низкому доходу. Иных вариантов нет.
Конечно, доходная линия не имеет ничего общего с физическим пространством, в котором мы с вами можем гулять, но это всё равно измерение. И (по крайней мере, в принципе) у него нет окончания ни в одной из сторон: нет (в принципе) ограничений на то, сколько денег человек может заработать или потерять за год. Этот одномерный мир не такой уж и разнообразный, но всё равно мы можем задать о нём несколько осмысленных вопросов:
- Как распределяются в США ежегодные доходы?
- Какой средний годовой доход в Японии?
- Как ответы на эти вопросы меняются со временем?
Эти вопросы приобретают смысл в одномерном мире доходной линии.
Радужное измерение
А вот ещё один, совсем другой мир. Единое измерение формируют цвета радуги, от красного, через оранжевый, к жёлтому, оттуда к зелёному, [голубому], синему и к фиолетовому [у англоговорящих людей шесть цветов в радуге, они не выделяют голубой / прим. перев.]. С этой точки зрения цвета формируют одномерный мир конечного размера. За пределами красного или фиолетового цвета есть невидимые формы цветов, но с точки зрения ваших глаз измерение заканчивается на них. Теперь оно представлено не в виде бесконечной линии, но в виде отрезка — «радужной линии» на рис. 2. Просьба не путать его с цветовым колесом — если оно замкнутое, то наше измерение начинается с красного цвета и заканчивается на фиолетовом. И вновь положение на радужной линии определяется одной единицей информации (цветом), и оно непрерывно.
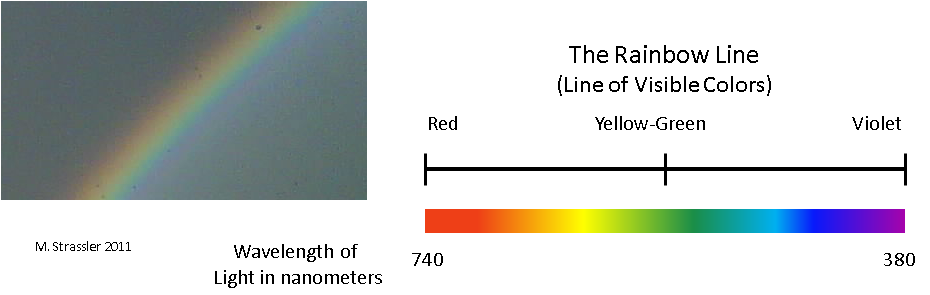
Рис. 2
Это, очевидно, также не измерение физического пространства! Можно бросить мячик из вашего дома в дом вашего соседа, но нельзя представить, как вы бросаете мячик из зелёного в оранжевое — это не имеет смысла. И всё равно это тоже будет измерение. Здесь можно задать множество осмысленных вопросов: как двигается цвет яблока по радужной линии в процессе превращения яблока из зелёного в красное? Сколько в солнечном свете каждого из цветов? Если оранжевая звезда начнёт превращаться в красную, станет ли она сначала жёлтой?
Измерение направления ветра
А вот третий вариант измерения, и опять другой. Если послушать прогноз погоды, то вам скажут, что ветер скоро начнёт дуть с севера, или с северо-запада, или с юго-запада. Возможные направления ветра — это тоже измерение. Обратите внимание, что это не пространственное измерение! В этом измерении нельзя бросить мячик так, как вы бросаете его вверх, влево или вперёд. Это измерение направлений в пространстве!
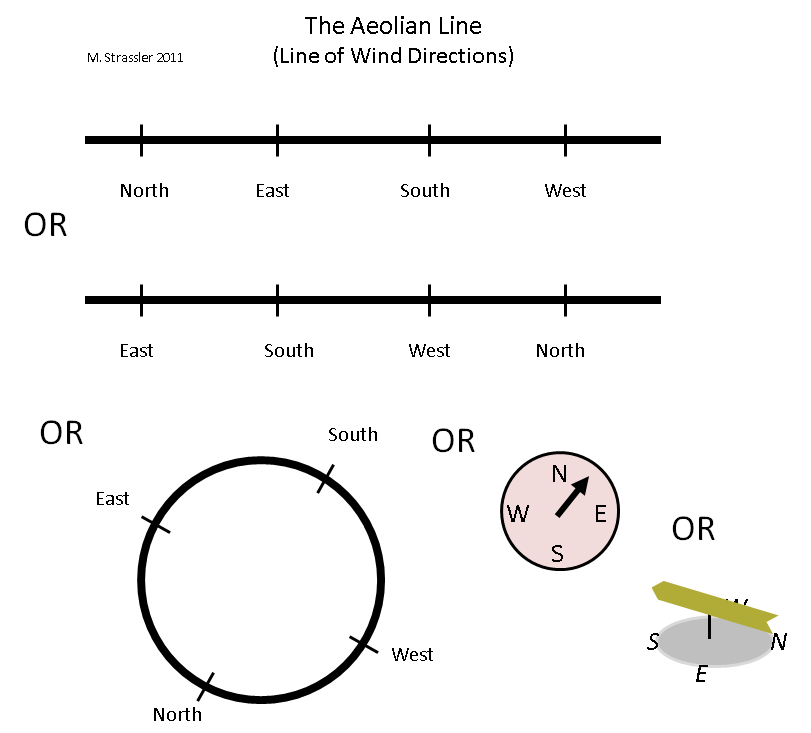
Рис. 3
Как можно представить это измерение? Для этого есть по меньшей мере два естественных способа, показанных на рис. 3. Один использует отрезок — «эолову линию» (Эол — полубог, властитель воздушных стихий у Древних греков) — но эолова линия отличается от радужной линии своей периодичностью. Направление ветра может меняться с северного на восточное, потом на южное, потом на западное, и потом опять на северное, непрерывно. И в нашем представлении линию можно разрезать где угодно — сравните две линии наверху рис. 3, которые одинаково хорошо представляют эолову линию. Суть в том, что ветер может переходить с правого конца линии сразу на левый конец, и наоборот, поэтому всё равно, где её разрезать. Или, возможно, легче всего представлять эту периодическую линию в виде круга. Именно это мы и делаем с компасом или флюгером!
Три разных одномерных мира
И вот вам одномерные миры. Посмотрите, насколько они богаты деталями! Разные размеры, разные свойства. На линии дохода доход может расти или уменьшаться вечно. На радужной линии ваши глаза могут перемещаться только до фиолетового, или же в другую сторону, только до красного. А на эоловой линии ветер может совершать полный круг сколько угодно — но при этом он всё время будет возвращаться на одно из направлений.
Эти разновидности одномерных миров — бесконечный, конечный, и конечно-периодический, представленные бесконечной линией, отрезком и кругом — базовые ингредиенты для понимания миров высших измерений. Я буду обращаться к ним ещё не раз. На рис. 4 представлены они, а также и четвёртый тип, простирающийся бесконечно только в одном направлении. Примером такого измерения может быть температура: она может быть сколь угодно большой, но существует минимально возможная температура — абсолютный ноль — поэтому температура образует линию, начинающуюся в абсолютном нуле и идущую оттуда вверх, но не вниз.
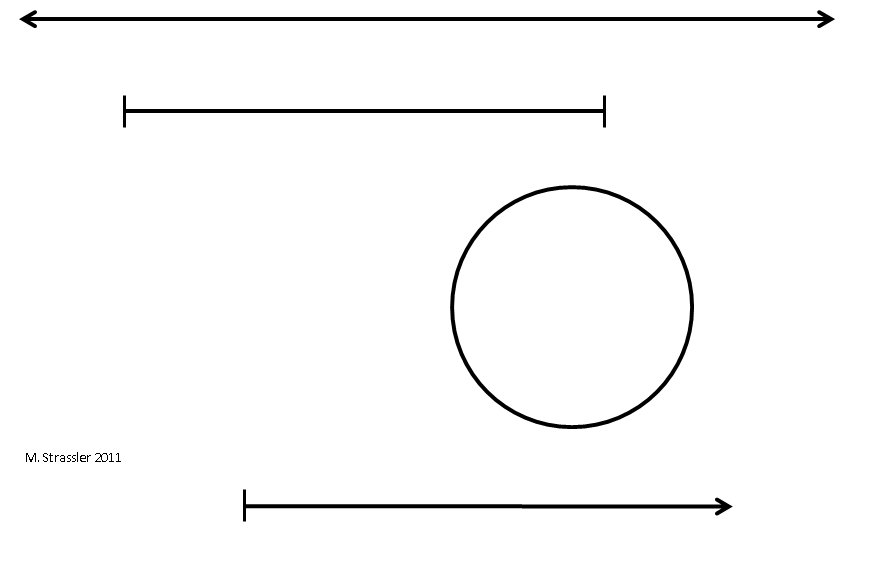
Рис. 4
Как изображать измерения, пространственные и прочие
Я вскользь упоминал или использовал несколько разных методов представления измерений. Доход можно представлять числом или бесконечной линией. Видимую радугу можно представить как отрезок, или как цвет, а также использовать число — длину волны фотонов, соответствующую определённому цвету. Направление ветра можно представлять кругом, или отрезком, чей левый конец соединён с правым — или словами типа север, восток, юг, запад — ила числом, определяющим направление в градусах, идущим от 0 до 360 и обратно на 0. То, что мы можем представлять одно измерение множеством разных способов даёт нам огромную гибкость для тренировки интуитивной работы с дополнительными измерениями.
Для иллюстрации этих видов измерений я выбрал понятия, никак не связанные с физическим пространством — доход, цвет радуги, направление ветра — чтобы показать, что пространственные измерения представляют собой конкретные примеры более общей концепции измерения. Понимание этого факта сильно облегчает попытки представить миры с количеством измерений более трёх. Помните, я упоминал две части процесса обучения мышлению о дополнительных измерениях? Во-первых, научитесь их представлять; во-вторых, поймите, как в них всё устроено и работает. У пространственных измерений есть особенности, связанные с тем, как некоторые вещи в них работают, но не с их представлением.
Пространственные миры с одним эффективным измерением
Учитывая всё это, рассмотрим регулярно встречаемые нами пространственные миры с одним эффективным измерением. Или, точнее, такие ситуации, в которых определённый аспект нашего мира ведёт себя так, как будто у пространства есть только одно измерение. Тогда мы говорим, что мир для определённых участников или объектов становится эффективно одномерным.
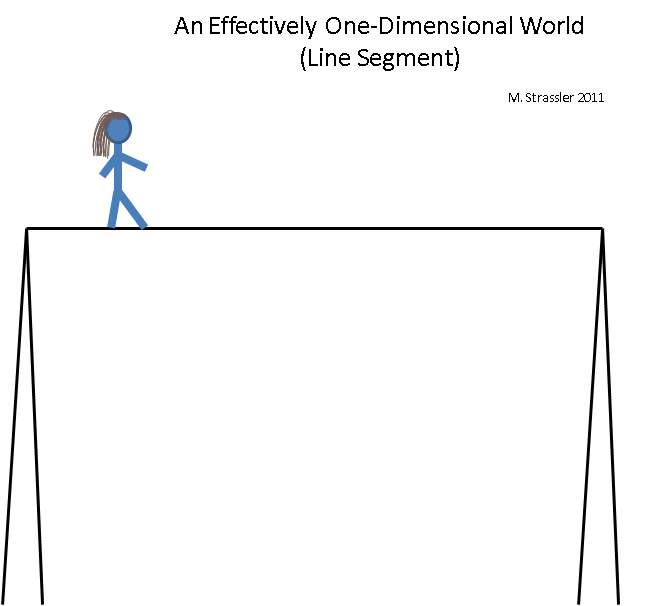
Рис. 5
Представьте себе канатоходца, балансирующего на высоко расположенном канате. Мир канатоходца эффективно одномерный (хотя он, конечно, на самом деле остаётся трёхмерным), поскольку он не способен безопасно двигаться в любом направлении, отличном от справа налево или слева направо. Этот мир похож на радужный мир — он конечен по длине, и когда канатоходец доходит до конца, ему надо развернуться и идти обратно (или сойти с каната, закончив ситуацию, в которой мир становится эффективно одномерным). Что ещё можно сказать? Положение на канате можно определить одной единицей информации (например, расстоянием от левого шеста до канатоходца). Два канатоходца могут встретиться на одной линии, но не пройти мимо друг друга.
Мы можем превратить мир каната в эолову линию, замкнув его в круг (рис. 6). В нём два канатоходца тоже не могли бы пройти мимо друг друга — это основное свойство одномерных миров. И это всё ещё было бы конечное измерение. Но канатоходец в такой ситуации уже мог бы ходить по кругу непрерывно и бесконечно, не останавливаясь.
Рис. 6
Другие известные нам (эффективно) одномерные миры:
- Узкая дорога — одномерный мир для автомобилей;
- Узкая тропа с обрывом — для карабкающегося в гору туриста;
- Этажи высотного здания — для лифта.
В целом мир остаётся трёхмерным, но для описания автомобилей, туриста или лифта необходимо представлять только одно измерение.
В дальнейшем помните: мы живём в кажущемся трёхмерном мире, и всё, что мы встречаем, кажется нам трёхмерным. Но иногда наш трёхмерный мир (точнее, его часть) может вести себя как эффективно одномерный, или двумерный (можете ли вы придумать примеры?) или даже нольмерный! (Каждый, кому не повезло когда-нибудь застрять в пробке, которая никуда не двигается, знает, каков этот мир с нулём измерений!) Эта интуиция позже будет нам очень полезной.
Комментарии (48)
NeoCode
06.12.2017 10:26Интереснее было бы про многомерное время:) с пространством все достаточно просто (ну разве что экстраполировать мерность на нецелые, отрицательные и прочие ненатуральные числа)
ankh1989
06.12.2017 11:58Что мешает ему быть многомерным? Если считать, что мир постоянно делится на ветки возможных развитий событий, то время это такое "дерево" в программистском понимании, а размерность времени это "скорость" с которой растёт количество вариантов (если кол-во вариантов через время
tравноt^dто размерность будетd).NeoCode
06.12.2017 12:01Интересно представить работу разума в многомерном времени. Я кстати представил, довольно интересно получилось.
ankh1989
06.12.2017 21:57Там ниже интересная статья которая говорит о том, что будет если время будет многомерное. Разума там похоже не будет потому что невозможно будет ничего предсказать.
maslyaev
06.12.2017 13:55+1Ветвящаяся одномерность — это тоже одномерность. Просто плюс ещё один вариант в дополнение к тому, что в статье показано на рис. 4.
Num
06.12.2017 20:51Элементарные частицы становятся нестабильными, образование сложных структур становится невозможным. (предположительно)
Another interesting difference, which can be shown by an elegant geometrical argument [10], is that particles become less stable when m > 1. For a particle to be able to decay when m = 1, it is not sufficient that a set of particles with the same quantum numbers
exists. It is also necessary, as is well known, that the sum of their rest masses should be
less than the rest mass of the original particle, regardless of how great its kinetic energy
may be. When m > 1, this constraint vanishes [10]. For instance,
• a proton can decay into a neutron, a positron and a neutrino,
• an electron can decay into a neutron, an antiproton and a neutrino, and
• a photon of sufficiently high energy can decay into any particle and its antiparticle.
Victor_koly
07.12.2017 00:15Почему размерность должна быть 2<N<3 для хороших астрономических условий — это легко показать. Правда в ОТО кажется те же условия хорошей размерности, но по точно противоположным причинам © Вики.
maslyaev
06.12.2017 13:51Концепцию двумерного времени довольно часто использую при проектировании информационных систем. Весьма полезный рабочий инструмент. Тема называется «Темпоральные базы данных».
leshabirukov
06.12.2017 22:50Филогенез (эволюция вида) и онтогенез (индивидуальное развитие организма).
velovich
06.12.2017 10:35Я мысленно представляю себе четырехмерное пространство вот как. Беру некий объем трехмерного пространства с объектами, еще одну точную копию его размещаю в его же объеме, но с минимальным смещением по любой оси. Представляю, что этих копий бесконечное множество, со смещением в эту же сторону. Потом сдвигаю все эти копии как гармошку в одни координаты. Получается то же самое трехмерное пространство, но мой мозг уже чувствует в нём четвертое измерение
vassabi
06.12.2017 11:02а следующим шагом — нужно мысленно поменять одну из осей в объеме всех трехмерных пространств на 4ю ось (по которой смещали). Потом представить, что там находится какой-нибудь 3хмерный шарик (или хотя бы точка), запомнить его траекторию, проделать обратное преобразование осей и увидеть — как оно будет выглядеть в проекциях :)
vassabi
06.12.2017 11:12но мне кажется, что чаще всего физики смотрят — по какому направлению меньше всего изменений, чтобы их отбросить и решать задачу в пространстве с меньшими измерениями: теплопередачу между двумя 3х-мерными поверхностями сводят к 2мерной (со словами «представим, что они бесконечной ширины»), или вихри вокруг (бесконечно длинного) крыла, и т.д.
eatfears
06.12.2017 13:05Всё хорошо, пока не попытаться повращать эту фигуру, строить сечения различными пространствами. Кажется, что без этого представление о фигуре не совсем полное.
Tyusha
06.12.2017 11:11Статья какая-то слишком уж для «чайников». Если вам как мне эта заметка на столь волнующую тему показалась банальной, то для расширения сознания и тренировки многомерного мышления, рекомендую узнать, что такое символы Шлефли.
На Хабре была отличнейшая статья с замечательными картинками на эту тему. Как правильно начинает автор: «Прочитав эту статью, вы уже не сможете смотреть на мир по старому». Чтение требует небольших усилий, но зато раскрываются верхние чакры. Очень рекомендую.
Shkaff
06.12.2017 13:27Ох, и как теперь разучиться? Работать надо…
А вообще, очень здорово, спасибо за ссылку.
bro-dev
06.12.2017 12:25Есть много вещей на которые мозг просто не приспособлен представлять, и поэтому лучше даже не пытаться, это не дает нечего.
Пытаться представить это значит совершить мысленный эксперимент, но если этот объект не поддается этому то такие хаки и костыли, просто фальсифицируют его. Так что самый верный вариант это заткнуться и считать.vassabi
06.12.2017 12:44Так что самый верный вариант это заткнуться и считать.
Но ведь, если сначала придумать более наглядное представление, то потом можно гораздо больше посчитать, чем без него
Nuwen
06.12.2017 12:38+3Просто оставлю
kisaa
06.12.2017 12:48+2Инженер три часа просидел на лекции математика, посвященной многомерным пространствам. В конце он, очень огорченный, подошел к лектору и сказал: «Извините, я хотел бы хоть немножко представить себе предмет вашей лекции. Но я не могу вообразить сферу в девятимерном пространстве!» «Это же очень просто, — ответил ему математик, — вообразите сферу в N-мерном пространстве, а затем положите N равным девяти».
Victor_koly
06.12.2017 15:09Есть интересная задачка. Берем куб с ребром a, вписываем 8 сфер диаметра a/2. Потом вписываем внутрь сферу, которая касается снаружи внутренних сторон этих сфер. Считаем радиус R этой сферы как функцию размера ребра a.
Экстраполируем на случай больших размерностей. Внезапно получаем, что в пределе R>a (хотя в начале эта функция падает).Tyusha
06.12.2017 15:44Решила. Только в начале ничего не убывает.
Пусть центр N-куба находится в начале N-мерных координат: (0, 0, 0, ...). Тогда центры шаров находятся в координатах вида a/4*(-1, -1, -1, ...), a/4*(1, -1, -1,...). Короче говоря, во всех возможных комбинациях -1 и 1, коих для N-мерного пространства 2^N.
Наш вписанный шарик находится, очевидно, в начале координат. Он должен касаться всех шаров. Для 2D и 3D это очевидно. В высших измерениях это можно доказать из симметрии задачи. (Если центральный шар касается шара X, но не касается шара Y, то поворотом всей системы можно поместить шар X на место Y… — Приходим к противоречию, что центральный шар касается только одного из них — должен касаться каждого.)
Центральный шар, таким образом, должен касаться диаметрально противоположных шаров и находиться на отрезке, соединяющих их центры. Большая диагональ — это в отрезок [ a/4*(-1, -1, -1,...); a/4*(1, 1, 1,...) ]. Его длина по теореме Пифагора a/2*sqrt(N).
Таким образом диаметр центрального шарика равен длине этого отрезка минус два радиуса «больших» шаров, т.е. a/2*(sqrt(N)-1). В 9-мерном и более пространствах радиус вписанного шарика становится больше куба.Tyusha
06.12.2017 15:52Думаю, это можно объяснить такой аналогией. В 9-мерном пространстве куб становится таким «пухлым», что его внутренности имеют линейный размер больше его стороны. Я себе представила наш родной шестиугольник со стороной 'a'. Очевидно, что в него можно вписать окружность диаметром больше 'a'. Вот и гиперкубы с какого момента становятся — это такие же «толстые» фигуры.
В общем интересный момент, не знала, надо будет запомнить.
UPD: В последнем предложении решения задачи слово «радиус» заменить на «диаметр».Tyusha
06.12.2017 19:10Подумала ещё, поняла, что глупость написала. То, что центральный шар (тип 2, для определённости повествования) вписан касательным к шарам (тип 1), расположенным внутри гиперкуба, ещё не означает, что этот центральный шар типа 1 будет целиком помещаться внутри куба! Да-да шары типа 2 находятся внутри гиперкуба, а шар тип 1, который вроде как в низких размерностях зажат внутри них, в высоких размерностях по-прежнему «зажат», но всё равно вылазит за пределы гиперкуба.
Это невозможно показать, но я попробую изобразить своё понимание:
Шарики типа 2 изобразила (в каком-то двухмерном сечении всей этой задачи) маленькими, хотя на самом деле они диаметром a/2 и касаются друг друга. При этом касающийся их всех шар тип 1 вылазит за пределы куба.
speakingfish
07.12.2017 11:28Если продолжать аналогии — то многомерный куб можно представить примерно как звёздчатый многогранник, но не с плоскими а с вогнутыми внутрь гранями и соответственно на плоском «срезе» надо изобразить звёздообразную фигуру с плавными вогнутыми внутрь линиями из уголков «звезды».
Victor_koly
07.12.2017 12:46Если хотите потренировать многомерное мышление (вдруг у Вас оно есть), то «нарисуйте» для 4-мерного куба 1-, 2-, 3-ю зоны Брилюэна.
Tyusha
06.12.2017 15:59Вы знали, вы знали про девять измерений (см. задачу выше). :)
Victor_koly
06.12.2017 18:17Значит объявляем наше пространство-время 10-мерным (9+время). Правда все свернуто должно быть.
Skigh
06.12.2017 15:23[у англоговорящих людей шесть цветов в радуге, они не выделяют голубой / прим. перев.]
Вообще-то они, начиная с сэра Айзека, выделяют 7 цветов, в том числе синий/голубой и индиго:
ru.wikipedia.org/wiki/Roy_G._Biv
PavelZhigulin
06.12.2017 20:41Меня вот заинтересовал вот такой вопрос. Возьмем одномерное прямое пространство. В нем движутся точки, которые не могут друг друга обойти. Двухмерное существо может перепрыгнуть через одномерное, но для последнего этот прыжок будет выглядеть как исчезновение в одном месте и появление в другом, т.е. как бы телепортацией. Однако, двумерное существо на самом деле пройдет больший путь, т.к. двигалось по дополнительной оси и его траектория точно длиннее. Очевидно, что единственный вариант, когда такая телепортация будет иметь смысл — если наше одномерное пространство не прямая линия, а, например, круг.
Получается, вся эта история применима и к случаю 3х и 4х мерного пространства. Для нас четырехмерный обьект просто телепортируется, но по факту этот обьект прошел большее расстояние в своем четвертом измерении, тратя на это перемещение большее время.
Собственно вопрос: где-то на ГТ читал, что на данный момент кривизну нашего пространства считают равной нулю. Получается, что мы живем в трехмерном аналоге прямой линии. Означает ли это, что телепортация для нас принципиально не имеет смысла, т.к. время на преодоление расстояния будет бОльшим, нежели просто пройтись пешком до нужной точки?Victor_koly
06.12.2017 22:12Если нет никаких протяженных измерений, путь по которым можно «согнуть». Если точнее — согнуть нужно все пространство (скажем 3-мерный «лист» в 4-мерном пространстве).
Само собой — идея далеко не новая, лет 20 по НФ на экране витает.
P.S. Кривизна пространства — это все же немного не то, но как объяснить что это за запись:
Тензор кривизны.
Тензор Ричи.
Скалярная кривизна.
В глобальных масштабах эта кривизна достаточна малая. Скажем в объеме войдов. Но и в обычных условиях скажем от гравитации Солнца или Земли Вы не заметите существенной кривизны пространства.Tyusha
07.12.2017 02:55Это называется внешняя кривизна. Плоское поространство можно вложить в пространство большей размерности разными способами, в том числе и согнутом виде. Жителям плоского пространства это всё равно, но отдалённые точки в их мире могут оказаться рядом в гипер-измерении. Аналогия, верно замечено — плоский лист, согнутый пополам.
Другое дело, что добавив к нашей 3d плоской вселенной временную координату, мы не сможем говорить о близости точек из-за знаконеопределённости нормы в пространстве Минковского.
Tyusha
07.12.2017 03:02В глобальном масштабе пространсвенная часть Вселенной плоская, но локальные дефекты кривизны могут давать глобальные топологические эффекты — кротовые норы или червоточины.
Таким образом само по себе плоское в среднем пространство не исключает телепортации
Victor_koly
07.12.2017 10:10Червоточины считать не пробовал, но для варпа явно лучше иметь отрицательную плотность энергии. А в привычном смысле такую на нос корабля не нацепить.
kauri_39
06.12.2017 22:47У меня нет нужды представлять больше 5 измерений, поскольку считаю наш мир 5-мерным. Три геометрических измерения представить легко: это, допустим, условно выделенный в пространстве квадрат. Четвёртое измерение — время — представляется как постоянный рост объёма этого квадрата, ведь расширение Вселенной задаёт в ней общий ход времени, значит, любой объём пространства расширяется с течением времени.
Пятое измерение говорит о структуре расширяющегося пространства в этом квадрате и вокруг него. Наше 4-мерное пространство-время — производное от него. Чтобы его представить, надо в первую очередь мысленно посмотреть на пространство через увеличительное стекло и увидеть его кванты. Допустим, в виде упругих, стремящихся к расширению шариков. Но при этом мы увидим разные колебания этих шариков, поскольку через пространство с разной скоростью проходят разные волны. Это флуктуации плотности среды (эфира, вакуума). И чуть разойдутся от волн два или три шарика, как между ними возникает новый шарик — новый квант пространства. Такие новые шарики появляются постоянно — то тут, то там, и от этого любой условно выделенный объём пространства расширяется по закону Хаббла.
Но это ещё не пятое измерение, а его проявление. Чтобы его представить в полной мере, потребуется мысленный микроскоп и телескоп. Благодаря первому мы увидим, как между шарами — увеличенными квантами нашего пространства — мельтешат тоже взаимно сжатые, но очень мелкие шарики — кванты пространства предыдущего масштаба. И как только из-за флуктуации плотности нашего пространства у них появится достаточно времени, они тут же сливаются в один общий объём — в новый шар, который давит на соседние шары и в своей мере побуждает к расширению состоящее из шаров (увеличенных квантов) наше пространство.
Телескоп нам нужен для того, чтобы мысленно посмотреть за границы нашей расширяющейся Вселенной. Мы увидим, что со всех сторон к нашей Вселенной расширяются соседние вселенные-шары. И что сама она является таким же расширяющимся шаром — квантом более масштабного пространства. Это значит, где-то в этом более масштабном пространстве произошла некая флуктуация плотности, и теперь на её месте возникла и расширяется наша Вселенная.
К ней расширяются или уже взаимно сжатые старые вселенные — кванты масштабного пространства, или группа новых, ещё свободно расширяющихся вселенных. Второе означает, что флуктуация была очень крупной, и на её месте возникнут не только новые кванты этого пространства, но и частицы материи — как минимум фотоны (разумные вселенные).
Если мы возьмём более мощные микроскоп и телескоп, то в первый мысленно увидим ещё менее масштабные кванты — это, уже понятно, менее масштабные вселенные. А во второй — ещё более масштабные кванты — более масштабные вселенные. И так — без конца в сторону микро- и макро- масштабов. Вот эта бесконечность масштабов вселенных и есть пятое измерение. Что для нас длится доли секунды в микромире — протекает как космологические процессы для обитателей микровселенных. И космологические процессы в нашей Вселенной (а тем более — с участием соседних вселенных) мелькнёт за доли секунды для обитателей макровселенной.
Если трудно в таком виде представить 5 измерение, можно упростить задачу и воспользоваться частичной аналогией. В ней аналогом 5 измерения будет 3-е геометрическое, вертикальное измерение — высота, пространство будет плоским — двумерным (длина и ширина), а 4-м, как и у нас, будет время. Эта умозрительная аналогия имеет реальное, наблюдаемое воплощение, например, плёнку или однослойный ковёр растений ряски. Плёнка свободно расширяется с течением времени — наращивает свою площадь за счёт 3 вертикального измерения — толщи воды и воздуха. Это происходит потому, что на краях листьев ряски из молекул воды и воздуха формируются дочерние растения, они падают между взрослыми особями и продолжают расти, уплотняя плёнку и побуждая её к расширению.
Остающаяся в среднем неизменной при расширении плёнки её плотность является аналогом космологической постоянной. Понятно, что она будет расти, когда плёнка упрётся в берега водоёма, это аналог грядущего взаимного сжатия нашей группы расширяющихся вселенных. Плёнка ряски также удобна в представлении гравитации — притока пространства к поглощающей его материи. Кратковременным аналогом этого процесса служит затягивание ряской дырки, пробитой в ней камнем. "Для науки главное — наблюдение" (Из "Аватара").Neuyazvimy1
07.12.2017 01:18Думаете в нужном направлении. Только измерении 11.
en.wikipedia.org/wiki/M-theory
TheShock
07.12.2017 04:15Статья клевая, но закончилась слишком внезапно. Вроде как только разминка.
Два канатоходца могут встретиться на одной линии, но не пройти мимо друг друга.
Вот это не понял. Объясните, что вы имели ввиду? Вот два объекта в одном измерении проходят друг мимо друга:
Или в этой аналогии имеется ввиду, что для того, чтобы пройти они как раз используют второе измерение?
Но почему даже теоретически они не могут пройти друг сквозь друга в одном измерении?Victor_koly
07.12.2017 10:18Я подозреваю, что в теории 2 одномерных объекта могут туннелировтаь друг через друга. То если они состоят из заряженных частиц, то эффективная сила отталкивания двух тел может создать непреодолимый потенциальный барьер (практически бесконечной высоты).
akaChewy
08.12.2017 09:57Если я правильно понимаю теорию, то простейшим объектом одномерного мира является точка, которая, в теории, не имеет размера, а имеет лишь координату, а ещё, в теории, одну и ту же координату могут иметь бесконечно большое количество точек. Таким образом, точки могут спокойно двигаться по линии, как эти кошечки.
Только бесконечно большому количеству кошечек будет сложней, чем точкам.Victor_koly
08.12.2017 10:39Точки могут двигаться, если в нашем одномерном пространстве нет сил с эффективным радиусом бесконечность. Только есть одна проблема — в одномерном мире сила взаимодействия не зависит от расстояния. Значит потенциал принимает вид
U=a*r, где знак константы a зависит от того, рассматриваем мы силу притяжения или отталкивания.
ogoNEKto
07.12.2017 11:23Тема не расрыта! Как же, все-таки, эффективно работать с 4+ мерными пространствами?
Victor_koly
А теперь представьте, как повесить на 3-мерный объект размером в классический радиус электрона ещё 6 дополнительных измерений, координата по каждому из которых не превышает интервал планковской длины.
P.S. Ещё в Вики подберите теорию что бы решить, должна ли в этом объеме находиться замкнутая струна или разомкнутая.
Tyusha
Только трусливые Калаби вместе с Яу сворачивают лишние измерения. Сильные духом, слабые умом— работают «так».
Victor_koly
3-мерность пространства у нас работает на очень разных масштабах (закон обратных квадратов в смысле силы взаимодействия типа кулоновского и в смысле потока излучения от звезд).
Значит все придуманные 10-мерные пространства должны быть свернуты (в т. ч. — на космологическом масштабе простарнства и времени).