Предлагаю читателям «Хабрахабра» статью о том, как школьная физика и OpenCV позволяют сделать иллюзию волн на воде. Основная сложность состоит в выборе красивого уравнения и переносе эффекта преломления света на границе раздела сред из трехмерного мира на плоскую картинку.
Решение задачи можно разделить на два этапа:
Полагаю, из школьного курса физики все помнят, что круги на воде есть ни что иное, как распространение колебаний по поверхности воды. Строгий подход к решению задачи подразумевает решение дифференциального волнового уравнения в двухмерном пространстве, однако полная физическая достоверность в нашем случае не требуется — можно взять готовое решение из школьного учебника по физике или придумать свое уравнение.

где c – коэффициент затухания; L – длина волны; x0, y0 — координаты центра волны; t- время. Величину длины волны лучше изменять в зависимости от размеров картинки.
Из школьного курса помним, что косинус принимает значения [-1;1], однако интенсивность цвета [0;255], следовательно необходимо немного модифицировать нашу волновую функцию. Окончательно, яркость каждого пикселя на слое с волной задается следующим образом:
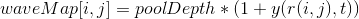
poolDepth – толщина слоя воды, в данном случае, еще и амплитуда волны в начальный момент времени. Слишком большое значение приведет к существенным искажениям изображения и будет некрасиво, слишком маленькое – почти не повлияет на картинку. Для картинки 100х100 подошло значение poolDepth=20, для картинки 1600x1600 оказалось возможным выставить предельное значение poolDepth=127.
Заметим, что размер волновой карты соответствует размеру исходного изображения. С учетом того, что волновая функция вычисляется в каждой точке получим гигантский объем вычислений уже для сравнительно небольшого изображения (в каждой точке вычисляем один квадратный корень, одну экспоненту и два косинуса – редкий ноутбук потянет картинку в 2МП при таком раскладе). На самом деле, в каждой точке явно вычислять и не нужно — уравнение ведь одномерное! На каждом временном шаге создаем таблицу значений волновой функции, а далее — линейная интерполяция.
Теперь имеем более или менее приличную реализацию алгоритма составления карты движения волны и можно приступать к ее наложению на исходное изображение.
Искажение изображения находящегося под водой происходит из-за преломления света на границе раздела. Фактически требуется решить школьную задачку о преломлении света на клине.
При нормальном падении света на ровную горизонтальную границу раздела сред искажения не происходит (изменения цвета картинки в результате интерференции здесь не рассматриваем – считаем, что лужа не глубокая да и на 100% физическую достоверность не претендуем).

На рисунке изображено что происходит с лучом света падающим на наклонную поверхность, необходимо найти насколько сместился выходящий луч относительно входящего. Расстояние CD и есть искомое смещение, определяемое как (решение здесь):
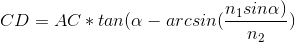
где n1=1 и n2=1.33 — показатели преломления первой (воздуха) и второй (воды) среды, соответственно.
Применительно к нашим волнам и пикселям уравнение можно записать как:
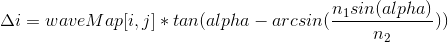
В данном случае, alpha есть угол наклона касательной к волне в точке [i,j], который вычисляется как:
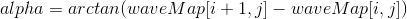
Разумеется, производную можно вычислить и аналитически, что повысит точность, однако это сделает трудоемким процесс изменения уравнения волны.
В данном случае, опять можем либо вычислять смещение для каждой точки изображения отдельно (void makeWaveMap(Mat&)), но лучше сделать lookup таблицу при первом вызове подпрограммы и использовать ее в дальнейшем (void makeWaveMapLUT(Mat&)).
Полный текст программы, а также тестовые изображения здесь.
Среднее время обработки (создание карты волны и наложение на исходное изображение) одного кадра для картинки размером 1600х1600 составило 0.137cек и 0.415сек c lookup таблицами и без них, соответственно (на видео картинка 100х100 пикселей).
Решение задачи можно разделить на два этапа:
- Создать карту распространения кругов/волн по воде;
- Совместить полученную карту с заданным изображением.
Карта волн
Полагаю, из школьного курса физики все помнят, что круги на воде есть ни что иное, как распространение колебаний по поверхности воды. Строгий подход к решению задачи подразумевает решение дифференциального волнового уравнения в двухмерном пространстве, однако полная физическая достоверность в нашем случае не требуется — можно взять готовое решение из школьного учебника по физике или придумать свое уравнение.

где c – коэффициент затухания; L – длина волны; x0, y0 — координаты центра волны; t- время. Величину длины волны лучше изменять в зависимости от размеров картинки.
Из школьного курса помним, что косинус принимает значения [-1;1], однако интенсивность цвета [0;255], следовательно необходимо немного модифицировать нашу волновую функцию. Окончательно, яркость каждого пикселя на слое с волной задается следующим образом:
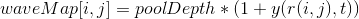
poolDepth – толщина слоя воды, в данном случае, еще и амплитуда волны в начальный момент времени. Слишком большое значение приведет к существенным искажениям изображения и будет некрасиво, слишком маленькое – почти не повлияет на картинку. Для картинки 100х100 подошло значение poolDepth=20, для картинки 1600x1600 оказалось возможным выставить предельное значение poolDepth=127.
Волновая карта без lookup таблицы
void makeWaveMap(Mat& image)
{
float simulPeriod = 10.0; // Period of simulation
static float time = 0.0;
const float dt = 0.05; // Time step
float poolDepth = 20.0;
int maxImageSize = image.cols > image.rows ? image.cols : image.rows;
for (int i = 0; i < image.rows; i++) {
for (int j = 0; j < image.cols; j++) {
float radius = sqrt((i - image.rows/2)*(i - image.rows/2) + (j - image.cols/2)*(j - image.cols/2));
float z = (1.0 + waveFunction(radius, time, maxImageSize))*poolDepth;
image.at<uchar>(i, j) = saturate_cast<uchar>(z);
}
}
time+= dt;
time*= (time < simulPeriod);
}
Заметим, что размер волновой карты соответствует размеру исходного изображения. С учетом того, что волновая функция вычисляется в каждой точке получим гигантский объем вычислений уже для сравнительно небольшого изображения (в каждой точке вычисляем один квадратный корень, одну экспоненту и два косинуса – редкий ноутбук потянет картинку в 2МП при таком раскладе). На самом деле, в каждой точке явно вычислять и не нужно — уравнение ведь одномерное! На каждом временном шаге создаем таблицу значений волновой функции, а далее — линейная интерполяция.
Волновая карта с lookup таблицей
void makeWaveMapLUT(Mat& image)
{
float simulPeriod = 10.0; // Period of simulation
static float time = 0.0;
const float dt = 0.05; // Time step
float poolDepth = 20.0;
int nLUT = image.cols > image.rows ? image.cols : image.rows;
int maxImageSize = nLUT;
float waveFuncLUT[nLUT];
for (int i = 0; i < nLUT; i++) {
float radius = saturate_cast<float>(i);
waveFuncLUT[i] = waveFunction(radius, time, maxImageSize);
}
for (int i = 0; i < image.rows; i++) {
for (int j = 0; j < image.cols; j++) {
float radius = sqrt((i - image.rows/2)*(i - image.rows/2) + (j - image.cols/2)*(j - image.cols/2));
int iRad = cvRound(radius);
float dR = radius - saturate_cast<float>(iRad);
float wF = waveFuncLUT[iRad] + (waveFuncLUT[iRad+1] - waveFuncLUT[iRad])*dR;
float z = (1.0 + wF)*poolDepth;
image.at<uchar>(i, j) = saturate_cast<uchar>(z);
}
}
time+= dt;
time*= (time < simulPeriod);
}
Теперь имеем более или менее приличную реализацию алгоритма составления карты движения волны и можно приступать к ее наложению на исходное изображение.
Наложение волновой карты на исходное изображение
Искажение изображения находящегося под водой происходит из-за преломления света на границе раздела. Фактически требуется решить школьную задачку о преломлении света на клине.
При нормальном падении света на ровную горизонтальную границу раздела сред искажения не происходит (изменения цвета картинки в результате интерференции здесь не рассматриваем – считаем, что лужа не глубокая да и на 100% физическую достоверность не претендуем).

На рисунке изображено что происходит с лучом света падающим на наклонную поверхность, необходимо найти насколько сместился выходящий луч относительно входящего. Расстояние CD и есть искомое смещение, определяемое как (решение здесь):
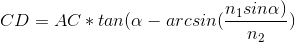
где n1=1 и n2=1.33 — показатели преломления первой (воздуха) и второй (воды) среды, соответственно.
Применительно к нашим волнам и пикселям уравнение можно записать как:
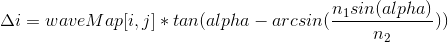
В данном случае, alpha есть угол наклона касательной к волне в точке [i,j], который вычисляется как:
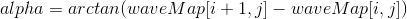
Разумеется, производную можно вычислить и аналитически, что повысит точность, однако это сделает трудоемким процесс изменения уравнения волны.
В данном случае, опять можем либо вычислять смещение для каждой точки изображения отдельно (void makeWaveMap(Mat&)), но лучше сделать lookup таблицу при первом вызове подпрограммы и использовать ее в дальнейшем (void makeWaveMapLUT(Mat&)).
Наложение без lookup таблицы
void blendWaveAndImage(Mat& sourceImage, Mat& targetImage, Mat& waveMap)
{
static float rFactor = 1.33; // refraction factor of water
for (int i = 1; i < sourceImage.rows-1; i++) {
for (int j = 1; j < sourceImage.cols-1; j++) {
float alpha, beta;
float xDiff = waveMap.at<uchar>(i+1, j) - waveMap.at<uchar>(i, j);
float yDiff = waveMap.at<uchar>(i, j+1) - waveMap.at<uchar>(i, j);
alpha = atan(xDiff);
beta = asin(sin(alpha)/rFactor);
int xDisplace = cvRound(tan(alpha - beta)*waveMap.at<uchar>(i, j));
alpha = atan(yDiff);
beta = asin(sin(alpha)/rFactor);
int yDisplace = cvRound(tan(alpha - beta)*waveMap.at<uchar>(i, j));
Vec3b Intensity = sourceImage.at<Vec3b>(i,j);
/* Check whether displacement fits the image size */
int dispNi = i + xDisplace;
int dispNj = j + yDisplace;
dispNi = (dispNi > sourceImage.rows || dispNi < 0 ? i : dispNi);
dispNj = (dispNj > sourceImage.cols || dispNj < 0 ? j : dispNj);
Intensity = sourceImage.at<Vec3b>(dispNi, dispNj);
targetImage.at<Vec3b>(i,j) = Intensity;
}
}
}
Наложение с lookup таблицей
void blendWaveAndImageLUT(Mat& sourceImage, Mat& targetImage, Mat& waveMap)
{
static float rFactor = 1.33; // refraction factor of water
static float dispLUT[512]; //Lookup table for displacement
static int nDispPoint = 512;
for (int i = 0; i < nDispPoint; i++) {
float diff = saturate_cast<float>(i - 255);
float alpha = atan(diff);
float beta = asin(sin(alpha)/rFactor);
dispLUT[i] = tan(alpha - beta);
}
nDispPoint = 0;
for (int i = 1; i < sourceImage.rows-1; i++) {
for (int j = 1; j < sourceImage.cols-1; j++) {
int xDiff = waveMap.at<uchar>(i+1, j) - waveMap.at<uchar>(i, j);
int yDiff = waveMap.at<uchar>(i, j+1) - waveMap.at<uchar>(i, j);
int xDisplace = cvRound(dispLUT[xDiff+255]*waveMap.at<uchar>(i, j));
int yDisplace = cvRound(dispLUT[yDiff+255]*waveMap.at<uchar>(i, j));
Vec3b Intensity = sourceImage.at<Vec3b>(i,j);
/* Check whether displacement fits the image size */
int dispNi = i + xDisplace;
int dispNj = j + yDisplace;
dispNi = (dispNi > sourceImage.rows || dispNi < 0 ? i : dispNi);
dispNj = (dispNj > sourceImage.cols || dispNj < 0 ? j : dispNj);
Intensity = sourceImage.at<Vec3b>(dispNi, dispNj);
targetImage.at<Vec3b>(i,j) = Intensity;
}
}
}
Полный текст программы, а также тестовые изображения здесь.
Результаты работы программы в картинках и цифрах
Среднее время обработки (создание карты волны и наложение на исходное изображение) одного кадра для картинки размером 1600х1600 составило 0.137cек и 0.415сек c lookup таблицами и без них, соответственно (на видео картинка 100х100 пикселей).


beeruser
А причём тут OpenCV?
>> гигантский объем вычислений уже для сравнительно небольшого изображения (в каждой точке вычисляем один квадратный корень, одну экспоненту и два косинуса
*смотрит на календарь*
www.shadertoy.com/view/XdsGDB
mikozh Автор
Согласен, погорячился с выносом OpenCV в название статьи, так как здесь ему отведена роль вспомогательная.
Изначальной целью было разобраться как можно более-менее красиво изобразить эффект преломления света на границе раздела сред в случае «плоской картинки»/фотографии. Здесь опять же вижу свою недоработку — нужно было четко формулировать цели и задачи.