Главная
Первое знакомство с сопроцессором Intel Xeon Phi

Первое знакомство с сопроцессором Intel Xeon Phi +15

07.07.2015 15:41

mikozh 8 13358 Источник

Желание познакомиться с сопроцессором Xeon Phi возникло давно, но то все не было возможности, то времени. В конце концов чудо свершилось и добрался до предмета вожделения. К сожалению, в руки попала далеко не самая последняя модель – 5110P, но для первого знакомства сойдет. Имея опыт работы с CUDA, меня очень интересовал вопрос отличий между программированием для GPU и сопроцессора. Вторым вопросом был: «А что (кроме дополнительной головной боли) я буду иметь используя сей девайс вместо GPU или CPU?».

Примечание: Данная статья не является рекламой или антирекламой какого-либо программного или аппаратного продукта, а всего лишь описывает личный опыт автора.

Мудрость из Developer’s Quick Start Guide

По сути, сопроцессор это отдельная железяка, устанавливающаяся в PCI-e слот. В отличие от GPU сопроцессор имеет свою Linux-подобную микро OS, так называемая Card OS или uOS. Существует два варианта запустить код на Xeon Phi:

Скомпилировать родной (native) код для архитектуры MIC, используя флаг –mmic
Запускать код через выгрузку (offload). В этом случае часть скомпилированного кода запускается на хосте (компьютер содержащий сопроцессор), а часть на девайсе (сопроцессор далее будем именовать просто девайсом).

Еще одним важным моментом является возможность использования OpenMP для распределения работы между потоками внутри девайса — прекрасно, этим и займемся. Сперва реализуем простой алгоритм на CPU, а затем переделаем программу так, чтобы она работала на сопроцессор.

Описание тестовой задачи

В качестве тестового примера была выбрана задача силового взаимодействия тел (n-body problem): есть N тел взаимодействие между которыми описывается неким парным потенциалом, необходимо определить положение каждого тела через некоторое время.
Потенциал и сила парного взаимодействия (в данном случае, можно взять любую функцию так как физика процесса нас интересует мало):

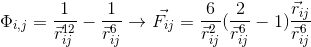
Алгоритм прост:

Задаем начальные координаты и скорости тел;
Вычисляем силу, действующую на каждое тело со стороны других;
Определяем новые координаты тел;
Повторяем шаги 2 и 3 пока не достигнем нужного результата.

Очевидно, что самым «тяжелым» этапом является именно расчет сил, так как требуется выполнить порядка N² операций, да еще и на каждом временном шаге (разумеется, применяя хитрости вроде списков соседей и вспомнив третий закон Ньютона можно существенно сократить число операций, но это отдельная история).
Серийный код такого алгоритма очень прост и легко преобразуется в параллельный используя директивы OpenMP.

Параллельный код с использованием OpenMP

/*---------------------------------------------------------*/
/*                  N-Body simulation benchmark            */
/*                   written by M.S.Ozhgibesov             */
/*                         04 July 2015                    */
/*---------------------------------------------------------*/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
#include <time.h>
#include <omp.h>

#define HOSTLEN 50

int numProc;

// Initial conditions
void initCoord(float *rA, float *vA, float *fA,                float initDist, int nBod, int nI);

// Forces acting on each body
void forces(float *rA, float *fA, int nBod);

// Calculate velocities and update coordinates
void integration(float *rA, float *vA, float *fA, int nBod);

int main(int argc, const char * argv[]) {
   int const nI = 32;               // Number of bodies in X, Y and Z directions
   int const nBod = nI*nI*nI;       // Total Number of bodies
   int const maxIter = 20;          // Total number of iterations (time steps)
   float const initDist = 1.0;      // Initial distance between the bodies
   float *rA;                       // Coordinates
   float *vA;                       // Velocities
   float *fA;                       // Forces
   int iter;
   double startTime0, endTime0;
   char host[HOSTLEN];

   rA = (float*)malloc(3*nBod*sizeof(float));
   fA = (float*)malloc(3*nBod*sizeof(float));
   vA = (float*)malloc(3*nBod*sizeof(float));

   gethostname(host, HOSTLEN);
   printf("Host name: %s\n", host);
   numProc = omp_get_num_procs();
   printf("Available number of processors: %d\n", numProc);

   // Setup initial conditions
   initCoord(rA, vA, fA, initDist, nBod, nI);

   startTime0 = omp_get_wtime();
   // Main loop
   for ( iter = 0; iter < maxIter; iter++ ) {
      forces(rA, fA, nBod);

      integration(rA, vA, fA, nBod);
   }

   endTime0 = omp_get_wtime();

   printf("\nTotal time = %10.4f [sec]\n", endTime0 - startTime0);

   free(rA);
   free(vA);
   free(fA);
	return 0;
}

// Initial conditions
void initCoord(float *rA, float *vA, float *fA,                float initDist, int nBod, int nI)
{
   int i, j, k;
   float Xi, Yi, Zi;
   float *rAx = &rA[     0];        //----
   float *rAy = &rA[  nBod];        // Pointers on X, Y, Z components of coordinates
   float *rAz = &rA[2*nBod];        //----
   int ii = 0;

   memset(fA, 0.0, 3*nBod*sizeof(float));
   memset(vA, 0.0, 3*nBod*sizeof(float));

   for (i = 0; i < nI; i++) {
      Xi = i*initDist;
      for (j = 0; j < nI; j++) {
         Yi = j*initDist;
         for (k = 0; k < nI; k++) {
            Zi = k*initDist;
            rAx[ii] = Xi;
            rAy[ii] = Yi;
            rAz[ii] = Zi;
            ii++;
         }
      }
   }
}

// Forces acting on each body
void forces(float *rA, float *fA, int nBod)
{
   int i, j;
   float Xi, Yi, Zi;
   float Xij, Yij, Zij;             // X[j] - X[i] and so on
   float Rij2;                      // Xij^2+Yij^2+Zij^2
   float invRij2, invRij6;          // 1/rij^2; 1/rij^6
   float *rAx = &rA[     0];        //----
   float *rAy = &rA[  nBod];        // Pointers on X, Y, Z components of coordinates
   float *rAz = &rA[2*nBod];        //----
   float *fAx = &fA[     0];        //----
   float *fAy = &fA[  nBod];        // Pointers on X, Y, Z components of forces
   float *fAz = &fA[2*nBod];        //----
   float magForce;                  // Force magnitude
   float const EPS = 1.E-10;         // Small value to prevent 0/0 if i==j

   #pragma omp parallel for num_threads(numProc) private(Xi, Yi, Zi,                Xij, Yij, Zij, magForce, invRij2, invRij6, j)
   for (i = 0; i < nBod; i++) {
      Xi = rAx[i];
      Yi = rAy[i];
      Zi = rAz[i];
      fAx[i] = 0.0;
      fAy[i] = 0.0;
      fAz[i] = 0.0;
      for (j = 0; j < nBod; j++) {
         Xij = rAx[j] - Xi;
         Yij = rAy[j] - Yi;
         Zij = rAz[j] - Zi;
         Rij2 = Xij*Xij + Yij*Yij + Zij*Zij;
         invRij2 = Rij2/((Rij2 + EPS)*(Rij2 + EPS));
         invRij6 = invRij2*invRij2*invRij2;
         magForce = 6.0*invRij2*(2.0*invRij6 - 1.0)*invRij6;
         fAx[i]+= Xij*magForce;
         fAy[i]+= Yij*magForce;
         fAz[i]+= Zij*magForce;
      }
   }
}

// Integration of coordinates an velocities
void integration(float *rA, float *vA, float *fA, int nBod)
{
   int i;
   float const dt = 0.01;              // Time step
   float const mass = 1.0;             // mass of a body
   float const mdthalf = dt*0.5/mass;
   float *rAx = &rA[     0];
   float *rAy = &rA[  nBod];
   float *rAz = &rA[2*nBod];
   float *vAx = &vA[     0];
   float *vAy = &vA[  nBod];
   float *vAz = &vA[2*nBod];
   float *fAx = &fA[     0];
   float *fAy = &fA[  nBod];
   float *fAz = &fA[2*nBod];

   #pragma omp parallel for num_threads(numProc)
   for (i = 0; i < nBod; i++) {
      rAx[i]+= (vAx[i] + fAx[i]*mdthalf)*dt;
      rAy[i]+= (vAy[i] + fAy[i]*mdthalf)*dt;
      rAz[i]+= (vAz[i] + fAz[i]*mdthalf)*dt;

      vAx[i]+= fAx[i]*dt;
      vAy[i]+= fAy[i]*dt;
      vAz[i]+= fAz[i]*dt;
   }
}

«Загружаем» сопроцессор

Рассмотрим нашу первоначальную программу. Сперва мы выясняем имя устройства и доступное количество процессоров. На рисунке ниже четко видны отличия между кодом для хоста (верхний рисунок) и девайса (нижний рисунок).

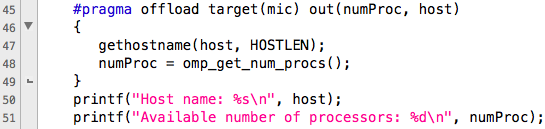
На нижнем рисунке видно, что для совершения выгрузки (offload) кода на девайс используется директива #pragma offload, в качестве цели для выгрузки указывается mic (наш девайс). Если в системе несколько сопроцессоров, то необходимо указать номер девайса. Пример:

#pragma offload target (mic:1)

После указания цели следуют параметры выгрузки, они могут быть:

in – переменные являются исключительно входными, то есть после завершения кода значения переменных обратно на хост не копируются.
out – переменные являются исключительно результатом, то есть перед началом работы выгружаемого участка их значения не копируются с хоста.
inout – перед запуском выгружаемого кода все переменные копируются на девайс, а после завершения – на хост.
nocopy – переменные никуда не копируются. Используется для повторного использования уже инициализированных переменных.

Подробное описание offload здесь.
В данном случае, переменные numProc и host только объявлены на хосте, но не инициализированы, поэтому используем out копирование (можно, конечно, и inout, но не будем нарушать порядок).
Полученный код вполне можно скомпилировать и запустить – никаких специальных флагов компиляции не требуется. В данном случае число потоков определит девайс, вернув значение numProc, в то время как расчеты будут все также производиться на хосте, так как мы еще не выгрузили процедуры.
Самая первая процедура задает начальные условия, она требует порядка N операций и вызывается только раз, поэтому оставим ее на хосте.
Далее запускается цикл по времени, на каждом шаге которого необходимо вычислять силы взаимодействия и интегрировать уравнения движения. Последняя процедура требует, как и задание начальных условий, порядка N операций, и казалось бы, что ее логично тоже оставить на хосте, но это потребует копирования массива с силами на каждом шаге. Очевидно, что при большом размере системы большая часть времени будет уходить на перетаскивание массива туда-обратно. Следовательно необходимо загрузить все исходные данные на девайс, произвести нужное число итераций и выгрузить результат на хост. Данный подход также используется при параллелизации для GPU.

   startTime0 = omp_get_wtime();
   // Main loop
   #pragma offload target(mic) inout(rA, fA, vA:length(3*nBod)) in(nBod)
   for ( iter = 0; iter < maxIter; iter++ ) {
      forces(rA, fA, nBod);
      integration(rA, vA, fA, nBod);
   }
   endTime0 = omp_get_wtime();

Помимо имен массивов здесь также необходимо указать их размер. Таким образом, цикл полностью загружается на девайс, исполняется на нем, после чего результаты копируются обратно. Следует отметить, что для подпрограмм, которые будут исполняться на девайсе необходимо указать соответствующие атрибуты:

// Initial conditions
void initCoord(float *rA, float *vA, float *fA,                float initDist, int nBod, int nI);

// Forces acting on each body
__attribute__ ((target(mic))) void forces(float *rA, float *fA, int nBod);

// Calculate velocities and update coordinates
__attribute__ ((target(mic))) void integration(float *rA, float *vA, float *fA, int nBod);

Вот, собственно и все, первая программа для Intel Xeon Phi готова и даже работает. При запуске программы может быть полезным узнать кто же именно и куда она копирует (между хостом и девайсом). Это можно сделать используя переменную среды OFFLOAD_REPORT. Пример (подробно):

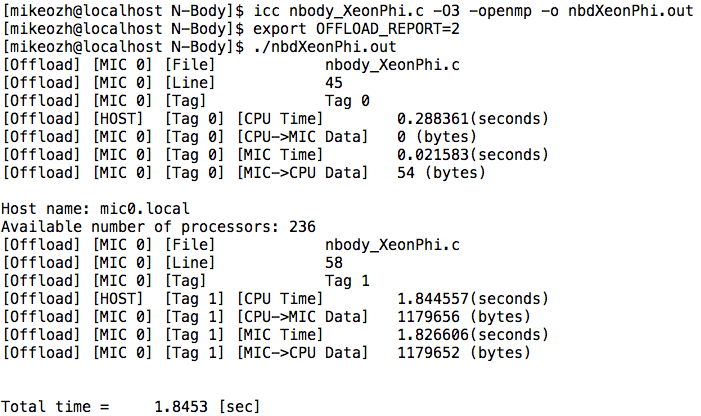
Видно, что в при первой выгрузке ничего не было скопировано на девайс, но с него было получено 54 байта (строка с именем и целое число – количество процессоров). Во втором случае (вторая выгрузка) было получено на 4 байта меньше чем отправлено, так как значение переменной nBod обратно не копировалось.
Время работы кода на 24 потоках хоста (2 процессора Intel Xeon E5-2680v3): 5.9832сек

Время работы кода на 236 потоках девайса (Intel Xeon Phi 5110P): 1.8667 сек

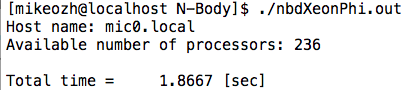
Итого, 2 строки кода дали прирост производительности почти в 3 раза – очень приятно. Следует отметить, что можно также рассмотреть вариант гибридных вычислений — часть задачи решается на хосте, часть на девайсе, однако здесь никак не избежать обменов данными между хостом и девайсом для синхронизации координат.

Полная версия кода для Xeon Phi

/*---------------------------------------------------------*/
/*                  N-Body simulation benchmark            */
/*                   written by M.S.Ozhgibesov             */
/*                         04 July 2015                    */
/*---------------------------------------------------------*/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
#include <time.h>
#include <omp.h>
#include <unistd.h>

#define HOSTLEN 50

__attribute__ ((target(mic))) int numProc;

// Initial conditions
void initCoord(float *rA, float *vA, float *fA,                float initDist, int nBod, int nI);

// Forces acting on each body
__attribute__ ((target(mic))) void forces(float *rA, float *fA, int nBod);

// Calculate velocities and update coordinates
__attribute__ ((target(mic))) void integration(float *rA, float *vA, float *fA, int nBod);

int main(int argc, const char * argv[]) {
   int const nI = 32;               // Number of bodies in X, Y and Z directions
   int const nBod = nI*nI*nI;       // Total Number of bodies
   int const maxIter = 20;          // Total number of iterations (time steps)
   float const initDist = 1.0;      // Initial distance between the bodies
   float *rA;                       // Coordinates
   float *vA;                       // Velocities
   float *fA;                       // Forces
   int iter;
   double startTime0, endTime0;
   double startTime1, endTime1;
   char host[HOSTLEN];

   rA = (float*)malloc(3*nBod*sizeof(float));
   fA = (float*)malloc(3*nBod*sizeof(float));
   vA = (float*)malloc(3*nBod*sizeof(float));

   #pragma offload target(mic) out(numProc, host)
   {
      gethostname(host, HOSTLEN);
      numProc = omp_get_num_procs();
   }
   printf("Host name: %s\n", host);
   printf("Available number of processors: %d\n", numProc);

   // Setup initial conditions
   initCoord(rA, vA, fA, initDist, nBod, nI);

   startTime0 = omp_get_wtime();
   // Main loop
   #pragma offload target(mic) inout(rA, fA, vA:length(3*nBod)) in(nBod)
   for ( iter = 0; iter < maxIter; iter++ ) {
      forces(rA, fA, nBod);
      integration(rA, vA, fA, nBod);
   }
   endTime0 = omp_get_wtime();

   printf("\nTotal time = %10.4f [sec]\n", endTime0 - startTime0);

   free(rA);
   free(vA);
   free(fA);
	return 0;
}

// Initial conditions
void initCoord(float *rA, float *vA, float *fA,                float initDist, int nBod, int nI)
{
   int i, j, k;
   float Xi, Yi, Zi;
   float *rAx = &rA[     0];        //----
   float *rAy = &rA[  nBod];        // Pointers on X, Y, Z components of coordinates
   float *rAz = &rA[2*nBod];        //----
   int ii = 0;

   memset(fA, 0.0, 3*nBod*sizeof(float));
   memset(vA, 0.0, 3*nBod*sizeof(float));

   for (i = 0; i < nI; i++) {
      Xi = i*initDist;
      for (j = 0; j < nI; j++) {
         Yi = j*initDist;
         for (k = 0; k < nI; k++) {
            Zi = k*initDist;
            rAx[ii] = Xi;
            rAy[ii] = Yi;
            rAz[ii] = Zi;
            ii++;
         }
      }
   }
}

// Forces acting on each body
__attribute__ ((target(mic))) void forces(float *rA, float *fA, int nBod)
{
   int i, j;
   float Xi, Yi, Zi;
   float Xij, Yij, Zij;             // X[j] - X[i] and so on
   float Rij2;                      // Xij^2+Yij^2+Zij^2
   float invRij2, invRij6;          // 1/rij^2; 1/rij^6
   float *rAx = &rA[     0];        //----
   float *rAy = &rA[  nBod];        // Pointers on X, Y, Z components of coordinates
   float *rAz = &rA[2*nBod];        //----
   float *fAx = &fA[     0];        //----
   float *fAy = &fA[  nBod];        // Pointers on X, Y, Z components of forces
   float *fAz = &fA[2*nBod];        //----
   float magForce;                  // Force magnitude
   float const EPS = 1.E-10;         // Small value to prevent 0/0 if i==j

   #pragma omp parallel for num_threads(numProc) private(Xi, Yi, Zi,                Xij, Yij, Zij, magForce, invRij2, invRij6, j)
   for (i = 0; i < nBod; i++) {
      Xi = rAx[i];
      Yi = rAy[i];
      Zi = rAz[i];
      fAx[i] = 0.0;
      fAy[i] = 0.0;
      fAz[i] = 0.0;
      for (j = 0; j < nBod; j++) {
         Xij = rAx[j] - Xi;
         Yij = rAy[j] - Yi;
         Zij = rAz[j] - Zi;
         Rij2 = Xij*Xij + Yij*Yij + Zij*Zij;
         invRij2 = Rij2/((Rij2 + EPS)*(Rij2 + EPS));
         invRij6 = invRij2*invRij2*invRij2;
         magForce = 6.0*invRij2*(2.0*invRij6 - 1.0)*invRij6;
         fAx[i]+= Xij*magForce;
         fAy[i]+= Yij*magForce;
         fAz[i]+= Zij*magForce;
      }
   }
}

// Integration of coordinates an velocities
__attribute__ ((target(mic))) void integration(float *rA, float *vA, float *fA, int nBod)
{
   int i;
   float const dt = 0.01;              // Time step
   float const mass = 1.0;             // mass of a body
   float const mdthalf = dt*0.5/mass;
   float *rAx = &rA[     0];
   float *rAy = &rA[  nBod];
   float *rAz = &rA[2*nBod];
   float *vAx = &vA[     0];
   float *vAy = &vA[  nBod];
   float *vAz = &vA[2*nBod];
   float *fAx = &fA[     0];
   float *fAy = &fA[  nBod];
   float *fAz = &fA[2*nBod];

   #pragma omp parallel for num_threads(numProc)
   for (i = 0; i < nBod; i++) {
      rAx[i]+= (vAx[i] + fAx[i]*mdthalf)*dt;
      rAy[i]+= (vAy[i] + fAy[i]*mdthalf)*dt;
      rAz[i]+= (vAz[i] + fAz[i]*mdthalf)*dt;

      vAx[i]+= fAx[i]*dt;
      vAy[i]+= fAy[i]*dt;
      vAz[i]+= fAz[i]*dt;
   }
}

Заключение

Единственное сходство между программированием для GPU и Xeon Phi, так это необходимость заботиться о перемещении данных между хостом и девайсом, собственно это же и является отличием от использования OpenMP исключительно для CPU. Хочется отметить, что родной компилятор умеет автоматически векторизовать код не только для хоста, но и для девайса, таким образом можно получить приличную производительность не сильно влезая в детали.
На мой взгляд, Xeon Phi хорошо подойдет если уже имеется готовый код работающий с OpenMP и необходимо повысить производительность, но нет желания/возможности переписывать для GPU. Важным моментом, который наверняка придется во вкусу людям из научной среды, является поддержка Fortran.

Полезные ссылки

www.prace-ri.eu/best-practice-guide-intel-xeon-phi-html
www.ichec.ie/infrastructure/xeonphi
www.cism.ucl.ac.be/XeonPhi.pdf
hpc-education.unn.ru/files/courses/XeonPhi/Lection03.pdf

Комментарии (8)

Krey
07.07.2015 20:42
#8490069
+2
А gcc это скомпилить можно?
1. Gumanoid
  07.07.2015 20:46
  #8490071
  Native для KNC можно, но будет работать медленно (по сравнению с ICC).
  
  Offload (с помощью OpenMP 4.x) для KNC нельзя, но можно будет для KNL.
  1. Krey
    07.07.2015 20:54
    #8490081
    С KNL все и так ясно — совместимость с Xeon полная, на нем все что угодно заработает. А вот с KNC маркетинговый отдел Интела немного покривил душой, его юзабельность не отличается от любой ARM или MIPS эмбедедовки (для обычного cpu-кода а не научных вычислений имеется ввиду).
1. grafmishurov
  07.07.2015 21:37
  #8490131
  У них на сайте есть страница «Intel and Third Party Tools and Libraries available with support for Intel® Xeon Phi™ Coprocessor», там и gcc, и gdb. У gcc сноска:
  
  *NOTE: Our changes to the GCC tool chain, available as of June 2012, allow it to build the coprocessor’s Linux environment, including our drivers, for the Intel® Xeon Phi(tm) Coprocessor. The changes do not include support for vector instructions and related optimization improvements. GCC for Intel® Xeon Phi(tm) is really only for building the kernel and related tools; it is not for building applications. Using GCC to build an application for Intel Xeon Phi Coprocessor will most often result in low performance code due its current inability to vectorize for the new Knights Corner vector instructions. Future changes to give full usage of Knights Corner vector instructions would require work on the GCC vectorizer to utilize those instructions’ masking capabilities

grafmishurov
07.07.2015 21:22
#8490113
Тут совсем не так как в CUDA. Таски железу раздает линуксовый Completely Fair Scheduler (из RBT), иерархия кешей, постраничная виртуальная память и CR3 регистр с адресом на директорию, как в их CPU. Но вроде бы Xeon Phi и OpenCL понимает, только неясно насколько OpenCL целесообразен с такой архитектурой железа. OpenMP и TBB наверное целесообразнее.

Вот выдержки из их guides:

Another example: while some traditional GPUs are based on HW scheduling of many tiny threads, Intel Xeon Phi coprocessors rely on the device OS to schedule medium size threads. These and other differences suggest that applications usually benefit from tuning to the HW they’re intended to run on.

The operating system createsdata structures known as page table data structures which the hardware uses to translate linear addresses into physical address. These page tabledata structures reside in the memory and created and managed by the operating system or micro-os in case of Intel Xeon Phi. There are four levels of page table data structures:

Page Global Directory
Page Upper Directory
Page Middel Directory
Page Table

atap3d
08.07.2015 00:08
#8490299
Вот только интересно, что быстрее, топовый GPU (может даже два), или сопостовимый по стоимости Xeon Phi?
1. Gumanoid
  08.07.2015 00:36
  #8490327
  Зависит от задачи (например, как много бранчей в циклах и т.п.)

mikozh Автор
08.07.2015 19:22
#8491537
+1
Пример задачи когда Xeon Phi лучше чем GPU: вычисление двух-элетронных интегралов (two-elecron integrals) в вычислительной квантовой механики. Вычисление требует большого количества промежуточных значений, для хранения которых shared memory кое-как хватает. Алгоритм реализовать, конечно можно, но трудозатраты очень больший и ускорение далеко не впечатляющее.
Пример задачи когда GPU лучше: молекулярная динамика. Код параллелится относительно не сложно (обычно трудности возникают при использовании нескольких GPU), а прирост производительности (по сравнению с CPU) десятки раз.

Первое знакомство с сопроцессором Intel Xeon Phi +15

Мудрость из Developer’s Quick Start Guide

Описание тестовой задачи

«Загружаем» сопроцессор

Заключение

Полезные ссылки

Комментарии (8)

Krey

Gumanoid

Krey

grafmishurov

grafmishurov

atap3d

Gumanoid

mikozh Автор