Если описать в паре предложений по какому принципу работают сортировки обменами, то:
- Попарно сравниваются элементы массива
- Если элемент слева* больше элемента справа, то элементы меняются местами
- Повторяем пункты 1-2 до тех пор, пока массив не отсортируется
* — под элементом слева подразумевается тот элемент из сравниваемой пары, который находится ближе к левому краю массива. Соответственно, элемент справа находится ближе к правому краю.
Сразу прошу прощения за повторение общеизвестного материала, вряд ли хоть один из алгоритмов в статье станет для Вас откровением. Про эти сортировки на Хабре писалось уже неоднократно (в том числе и мной — 1, 2, 3) и спрашивается, зачем опять возвращаться к этой теме? Но раз уж я решил написать связную серию статей про все сортировки на свете, мне приходится хотя бы в экспресс-варианте пройтись и по обменным способам. При рассмотрении следующих классов уже будет много новых (и мало кому известных) алгоритмов, заслуживающих отдельных интересных статей.
Традиционно к «обменникам» относят сортировки, в которых элементы меняются (псевдо)случайным образом (bogosort, bozosort, permsort и т.п.). Однако я не стал их включать в этот класс, так как в них отсутствуют сравнения. Про эти сортировки будет отдельная статья, где мы вдоволь пофилософствуем о теории вероятности, комбинаторике и тепловой смерти Вселенной.
Придурковатая сортировка :: Stooge sort
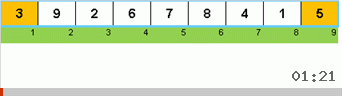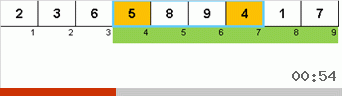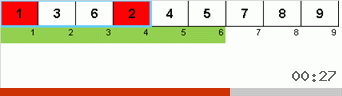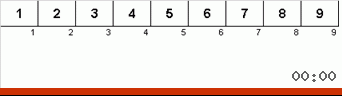
- Сравниваем (и при необходимости меняем) элементы на концах подмассива.
- Берём две трети подмассива от его начала и к этим 2/3 рекурсивно применяем общий алгоритм.
- Берём две трети подмассива от его конца и к этим 2/3 рекурсивно применяем общий алгоритм.
- И опять берём две трети подмассива от его начала и к этим 2/3 рекурсивно применяем общий алгоритм.
Изначально подмассив — весь массив. А дальше рекурсия дробит родительский подмассив на 2/3, производит сравнения/обмены на концах раздробленных отрезков и в итоге всё упорядочивает.
def stooge_rec(data, i = 0, j = None):
if j is None:
j = len(data) - 1
if data[j] < data[i]:
data[i], data[j] = data[j], data[i]
if j - i > 1:
t = (j - i + 1) // 3
stooge_rec(data, i, j - t)
stooge_rec(data, i + t, j)
stooge_rec(data, i, j - t)
return data
def stooge(data):
return stooge_rec(data, 0, len(data) - 1)Выглядит шизофренично, но тем не менее это на 100% корректно.
Вялая сортировка :: Slow sort
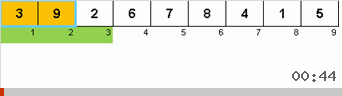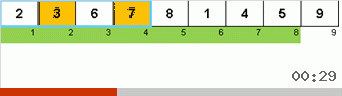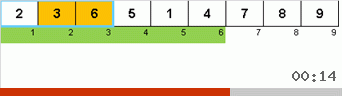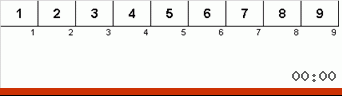
И здесь мы наблюдаем рекурсивную мистику:
- Если подмассив состоит из одного элемента, то завершаем рекурсию.
- Если подмассив состоит из двух и более элементов, то делим его пополам.
- Применяем рекурсивно алгоритм к левой половинке.
- Применяем рекурсивно алгоритм к правой половинке.
- Сравниваются элементы на концах подмассива (и меняются при необходимости).
- Рекурсивно применяем алгоритм к подмассиву без последнего элемента.
Изначально подмассив — это весь массив. А рекурсия будет дальше половинить, сравнивать и менять пока всё не отсортирует.
def slow_rec(data, i, j):
if i >= j:
return data
m = (i + j) // 2
slow_rec(data, i, m)
slow_rec(data, m + 1, j)
if data[m] > data[j]:
data[m], data[j] = data[j], data[m]
slow_rec(data, i, j - 1)
def slow(data):
return slow_rec(data, 0, len(data) - 1)Похоже на бред, однако массив упорядочивается.
Почему корректно работают StoogeSort и SlowSort?
Пытливый читатель задаст резонный вопрос: а почему эти два алгоритма вообще срабатывают? Они вроде простые, а не особо-то очевидно, что так можно что-то отсортировать.
Давайте сначала разберём Slow sort. Последний пункт этого алгоритма намекает, что рекурсивные усилия вялой сортировки направлены только на то, чтобы в правую крайнюю позицию поставить наибольший элемент в подмассиве. Это особенно заметно, если применить алгоритм к обратно упорядоченному массиву:
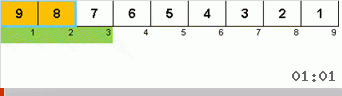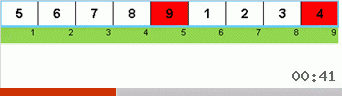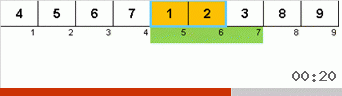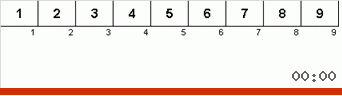
Хорошо видно, что на всех уровнях рекурсии максимумы быстро мигрируют вправо. Затем эти максимумы, оказавшиеся там где нужно, выключаются из игры: алгоритм вызывает сам себя — но уже без последнего элемента.
В Stooge sort происходит похожая магия:
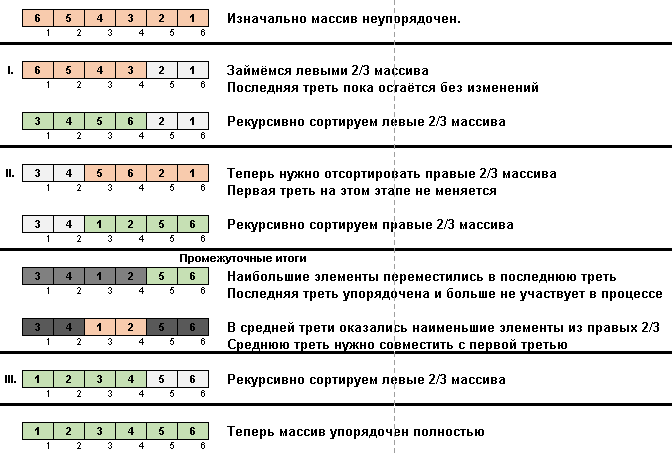
На самом деле тут тоже делается упор на максимальных элементах. Только Slow sort их в конец перемещают по одному, а Stooge sort треть элементов подмассива (самые крупные из них) задвигает в крайнюю справа треть ячеечного пространства.
Переходим к алгоритмам, где уже всё достаточно очевидно.
Туповатая сортировка :: Stupid sort

Очень осторожная сортировка. Она идёт от начала массива до конца и сравнивает соседние элементы. Если два соседних элемента пришлось поменять местами, то сортировка на всякий случай возвращается в самое начало массива и начинает всё заново.
def stupid(data):
i, size = 1, len(data)
while i < size:
if data[i - 1] > data[i]:
data[i - 1], data[i] = data[i], data[i - 1]
i = 1
else:
i += 1
return dataГномья сортировка :: Gnome sort

Почти то-же самое, но тут сортировка при обмене не возвращается в самое начало массива, а делает всего один шаг назад. Этого, оказывается, вполне достаточно чтобы всё отсортировать.
def gnome(data):
i, size = 1, len(data)
while i < size:
if data[i - 1] <= data[i]:
i += 1
else:
data[i - 1], data[i] = data[i], data[i - 1]
if i > 1:
i -= 1
return dataОптимизированная гномья сортировка

Но можно сэкономить не только на отступлении, но и при движении вперёд. При подряд нескольких обменах приходится делать столько же шагов назад. А потом приходится возвращаться обратно (сравнивая по пути элементы, которые и так упорядочены друг относительно друга). Если запоминать позицию, с которой начались обмены, то затем можно сразу же перепрыгнуть в эту позицию, когда обмены завершены.
def gnome(data):
i, j, size = 1, 2, len(data)
while i < size:
if data[i - 1] <= data[i]:
i, j = j, j + 1
else:
data[i - 1], data[i] = data[i], data[i - 1]
i -= 1
if i == 0:
i, j = j, j + 1
return dataПузырьковая сортировка :: Bubble sort

В отличие от глупой и гномьей сортировки при обмене элементов в пузырьковой никаких возвратов не происходит — она продолжает двигаться вперёд. Дойдя до конца, происходит перемещение наибольшего элемента массива в самый конец.
Затем сортировка повторяет весь процесс заново, в результате чего второй элемент по старшинству оказывается на предпоследнем месте. На следующей итерации третий по величине элемент оказывается третьим с конца и т.д.
def bubble(data):
changed = True
while changed:
changed = False
for i in range(len(data) - 1):
if data[i] > data[i+1]:
data[i], data[i+1] = data[i+1], data[i]
changed = True
return dataОптимизированная пузырьковая сортировка

Можно немного выгадать на проходах по началу массива. В процессе первые элементы оказывается временно упорядоченными друг относительно друга (эта отсортированная часть постоянно меняется в размерах — то уменьшается, то увеличивается). Это легко фиксируется и при новой итерации можно просто перепрыгнуть через группу таких элементов.
(Проверенную реализацию на Питоне добавлю сюда чуть позже. Не успел подготовить.)
Шейкерная сортировка :: Shaker sort

Разновидность пузырька. На первом проходе как обычно — задвигаем максимум в конец. Потом резко разворачиваемся и толкаем минимум в начало. Отсортированные крайние области массива увеличиваются в размерах после каждой итерации.
def shaker(data):
up = range(len(data) - 1)
while True:
for indices in (up, reversed(up)):
swapped = False
for i in indices:
if data[i] > data[i+1]:
data[i], data[i+1] = data[i+1], data[i]
swapped = True
if not swapped:
return dataЧётно-нечётная сортировка :: Odd-even sort

Снова итерации по попарному сравнению соседних элементов при движении слева-направо. Только сначала сравниваем пары у которых первый элемент — нечётный по счёту, а второй — чётный (т.е. первый и второй, третий и четвёртый, пятый и шестой и т.д.). А потом наоборот — чётный + нечётный (второй и третий, четвёртый и пятый, шестой и седьмой и т.д.). В этом случае многие крупные элементы массива на одной итерации одновременно делают один шаг вперёд (в пузырьке самый крупный за итерацию доходит до конца, но остальные немаленькие практически все остаются на месте).
Кстати, это изначально была параллельная сортировка со сложностью O(n). Надо будет в AlgoLab реализовать в разделе «Параллельные сортировки».
def odd_even(data):
n = len(data)
isSorted = 0
while isSorted == 0:
isSorted = 1
temp = 0
for i in range(1, n - 1, 2):
if data[i] > data[i + 1]:
data[i], data[i + 1] = data[i + 1], data[i]
isSorted = 0
for i in range(0, n - 1, 2):
if data[i] > data[i + 1]:
data[i], data[i + 1] = data[i + 1], data[i]
isSorted = 0
return dataСортировка расчёской :: Comb sort

Самая удачная модификация пузырька. Алгоритм по скорости соперничает с быстрой сортировкой.
Во всех предыдущих вариациях мы сравнивали соседей. А тут сначала рассматриваются пары элементов, находящиеся друг от друга на максимальном расстоянии. При каждой новой итерации это расстояние равномерно сужается.
def comb(data):
gap = len(data)
swaps = True
while gap > 1 or swaps:
gap = max(1, int(gap / 1.25)) # minimum gap is 1
swaps = False
for i in range(len(data) - gap):
j = i + gap
if data[i] > data[j]:
data[i], data[j] = data[j], data[i]
swaps = True
return dataБыстрая сортировка :: Quick sort

Ну и самый продвинутый обменный алгоритм.
- Делим массив пополам. Средний элемент — опорный.
- Движемся от левого края массива вправо, до тех пор пока не обнаружим элемент, который больше опорного.
- Движемся от правого края массива влево, до тех пор пока не обнаружим элемент, который меньше опорного.
- Меняем местами два элемента, найденные в пунктах 2 и 3 .
- Продолжаем выполнять пункты 2-3-4 пока в результате обоюдного движения не произойдёт встреча.
- В точке встречи массив делится на две части. К каждой части рекурсивно применяем алгоритм быстрой сортировки.
Почему это работает? Слева от точки встречи находятся элементы, меньшие или равные чем опорный. Справа от точки встречи находятся элементы большие или равные чем опорный. То есть, любой элемент из левой части меньше или равен любого элемента из правой части. Поэтому в точке встречи массив можно смело поделить на два подмассива и аналогично рекурсивно сортировать каждый подмассив.
def quick(data):
less = []
pivotList = []
more = []
if len(data) <= 1:
return data
else:
pivot = data[0]
for i in data:
if i < pivot:
less.append(i)
elif i > pivot:
more.append(i)
else:
pivotList.append(i)
less = quick(less)
more = quick(more)
return less + pivotList + moreK-сортировка :: K-sort
На Хабре опубликован перевод одной из статей, где сообщается о модификации QuickSort, которая на 7 миллионах элементов обгоняет пирамидальную сортировку. Кстати, само по себе это сомнительное достижение, ибо классическая пирамидальная сортировка не бьёт рекордов быстродействия. В частности, её асимптотическая сложность ни при каких условиях не достигает O(n) (особенность данного алгоритма).
Но дело в другом. По авторскому (причём, очевидно некорректному) псевдокоду вообще не понять какова, собственно, основная идея алгоритма. Лично у меня сложилось впечатление что авторы какие-то проходимцы, которые действовали по такому методу:
- Заявляем о изобретении супер-алгоритма сортировки.
- Подкрепляем заявление неработающим и непонятным псевдокодом (типа, умным и так ясно, а дуракам понять всё равно не дано).
- Приводим графики и табицы, якобы демонстрирующие практическую скорость алгоритма на больших данных. Ввиду отсутствия реально работающего кода всё равно никто не сможет ни проверить ни опровергнуть эти статистические выкладки.
- Публикуем ахинею на Arxiv.org под видом научной статьи.
- PROFIT!!!
Может, я зря наговариваю на людей и на самом деле алгоритм рабочий? Кто-нибудь может пояснить как работает k-sort?
UPD. Мои огульные обвинения авторов сортировки в мошенничестве оказались несостоятельными :) Пользователь jetsys разобрался в псевдокоде алгоритма, написал работающую версию на PHP и прислал мне её в личных сообщениях:
K-sort на PHP
function _ksort(&$a,$left,$right){
$ke=$a[$left];
$i=$left;
$j=$right+1;
$k=$p=$left+1;
$temp=false;
while($j-$i>=2){
if($ke<=$a[$p]){
if(($p!=$j) && ($j!=($right+1))){
$a[$j]=$a[$p];
}
else if($j==($right+1)){
$temp=$a[$p];
}
$j--;
$p=$j;
} else {
$a[$i]=$a[$p];
$i++;
$k++;
$p=$k;
}
}
$a[$i]=$ke;
if($temp) $a[$i+1]=$temp;
if($left<($i-1)) _ksort($a,$left,$i-1);
if($right>($i+1)) _ksort($a,$i+1,$right);
}Анонс
Это всё была теория, пора переходить к практике. Следующая статья — тестирование сортировок обменами на разных наборах данных. Мы узнаем:
- Какая сортировка наихудшая — придурковатая, вялая или туповатая?
- Сильно ли помогают оптимизации и модификации пузырьковой сортировке?
- При каких условиях медленные алгоритмы легко уделают по скорости QuickSort?
И когда мы выясним ответы на эти важнейшие вопросы, сможем приступить к изучению следующего класса — сортировок вставками.
Ссылки
Excel-приложение AlgoLab, с помощью которого можно в пошаговом режиме просмотреть визуализацию этих (и не только этих) сортировок.
Вики/Wiki —
Комментарии (8)

TheGodfather
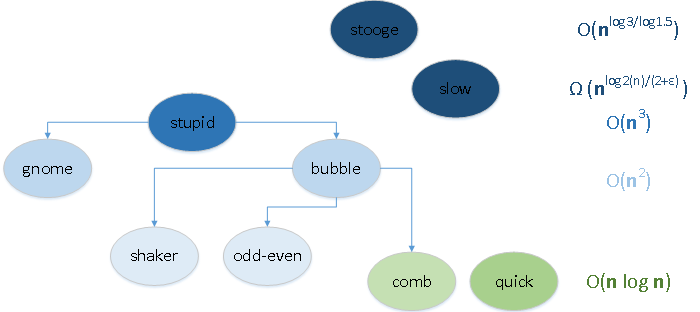
20.06.2018 14:16На картинке определенно не хватает Bogosort O(n!) и сортировки подсчетом (O(n)). Плюс стрелки проставлены как-то случайным образом, вообще непонятна логика.

valemak Автор
20.06.2018 16:25Я решил сортировки, в которых случайно перемешивается массив выделить в отдельную группу и рассказать про неё когда-нибудь отдельно.
Стрелки на КДПВ означают преемственность алгоритмов. Если видоизменить Stupid sort одним образом, то получается Gnome sort. Если другим — то получается Bubble sort. Bubble sort в свою очередь имеет свои модификации — Odd-Even sort, Shaker sort и Comb sort.


citizentwo
Вот начитаются студентики подобного материала — потом на работе практикуют!
vesper-bot
Вначале в учебе — помнится, первый семестр был как раз реализовать несколько сортировок. Потом на работе можно более основательно выбирать из имеющихся алгоритмов.
citizentwo
Одно дело если ты их сам писал и понял как они работают, а большинство просто копипастят с разнообразных источников, лижбы лабу или курсовую защитить — это уже обидно. В таком случае не вижу смысла в учебе на программиста. Система образования конечно таких отсеет, но она как и любая другая не идеальна.
PYXRU
Конечная идея образования научить делать так чтоб работало и правильно, а не научить писать самим сортировку.