02.07.2018 11:57
valemak 14 4000 Источник


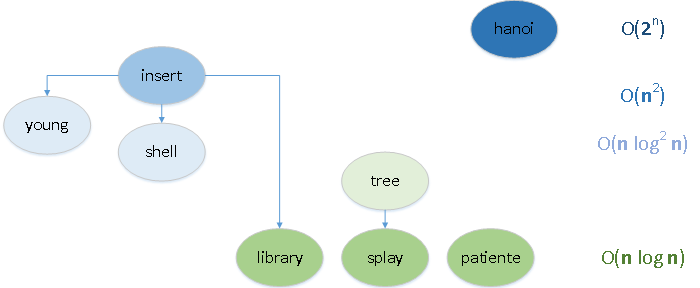
Общая суть сортировок вставками такова:

  1. Перебираются элементы в неотсортированной части массива.
  2. Каждый элемент вставляется в отсортированную часть массива на то место, где он должен находиться.

Это, в принципе, всё, что Вам нужно знать про сортировки вставками. То есть, сортировки вставками всегда делят массив на 2 части — отсортированную и неотсортированную. Из неотсортированной части извлекается любой элемент. Поскольку другая часть массива отсортирована, то в ней достаточно быстро можно найти своё место для этого извлечённого элемента. Элемент вставляется куда нужно, в результате чего отсортированная часть массива увеличивается, а неотсортированная уменьшается. Всё. По такому принципу работают все сортировки вставками.

Самое слабое место в этом подходе — вставка элемента в отсортированную часть массива. На самом деле это непросто и на какие только ухищрения не приходится идти, чтобы выполнить этот шаг.

Сортировка простыми вставками




Проходим по массиву слева направо и обрабатываем по очереди каждый элемент. Слева от очередного элемента наращиваем отсортированную часть массива, справа по мере процесса потихоньку испаряется неотсортированная. В отсортированной части массива ищется точка вставки для очередного элемента. Сам элемент отправляется в буфер, в результате чего в массиве появляется свободная ячейка — это позволяет сдвинуть элементы и освободить точку вставки.

def insertion(data):
	for i in range(len(data) - 1):
		j = i - 1 
		key = data[i]
		while data[j] > key and j >= 0:
			data[j + 1] = data[j]
			j -= 1
		data[j + 1] = key
	return data

На примере простых вставок показательно смотрится главное преимущество большинства (но не всех!) сортировок вставками, а именно — очень быстрая обработка почти упорядоченных массивов:



При таком раскладе даже самая примитивная реализация сортировки вставкам, скорее всего, обгонит супер-оптимизированный алгоритм какой-нибудь быстрой сортировки, в том числе и на больших массивах.

Этому способствует сама основная идея этого класса — переброска элементов из неотсортированной части массива в отсортированную. При близком расположении близких по величине данных место вставки обычно находится близко к краю отсортированной части, что позволяет вставлять с наименьшими накладными расходами.

Нет ничего лучше для обработки почти упорядоченных массивов чем сортировки вставками. Когда Вы где-то встречаете информацию, что лучшая временна?я сложность сортировки вставками равна O(n), то, скорее всего, имеются в виду ситуации с почти упорядоченными массивами.

Сортировка простыми вставками с бинарным поиском




Так как место для вставки ищется в отсортированной части массива, то идея использовать бинарный поиск напрашивается сама собой. Другое дело, что поиск места вставки не является критичным для временно?й сложности алгоритма (главный пожиратель ресурсов — этап самой вставки элемента в найденную позицию), поэтому данная оптимизация здесь мало что даёт.

А в случае почти отсортированного массива бинарный поиск может работать даже медленнее, поскольку он начинает с середины отсортированного участка, который, скорее всего, будет находиться слишком далеко от точки вставки (а на обычный перебор от позиции элемента до точки вставки уйдёт меньше шагов, если данные в массиве в целом упорядочены). 

def insertion_binary(data):
	for i in range(1, len(data) - 1):
		key = data[i]
		lo, hi = 0, i - 1
		while lo < hi:
			mid = lo + (hi - lo) // 2
			if key < data[mid]:
				hi = mid
			else:
				lo = mid + 1
		for j in range(i, lo + 1, -1):
			data[j] = data[j - 1]
		data[lo] = key
	return data

В защиту бинарного поиска отмечу, что он может сказать решающее слово в эффективности других сортировок вставками. Благодаря ему, в частности, на среднюю сложность по времени O(n log n) выходят такие алгоритмы как сортировка библиотекаря и пасьянсная сортировка. Но про них позже.

Па?рная сортировка простыми вставками


Модификация простых вставок, разработанная в тайных лабораториях корпорации Oracle. Эта сортировка входит в пакет JDK, является составной частью Dual-Pivot Quicksort. Используется для сортировки малых массивов (до 47 элементов) и сортировки небольших участков крупных массивов.



В буфер отправляются не один, а сразу два рядом стоя?щих элемента. Сначала вставляется больший элемент из пары и сразу после него метод простой вставки применяется к меньшему элементу из пары.

Что это даёт? Экономию для обработки меньшего элемента из пары. Для него поиск точки вставки и сама вставка осуществляются только на той отсортированной части массива, в которую не входит отсортированная область, задействованная для обработки большего элемента из пары. Это становится возможным, поскольку больший и меньший элементы обрабатываются сразу друг за другом в одном проходе внешнего цикла.

На среднюю сложность по времени это не влияет (она так и остаётся равной O(n2)), однако па?рные вставки работают чуть быстрее чем обычные.

Алгоритмы я иллюстрирую на Python, но тут приведу первоисточник (видоизменённый в целях читабельности) на Java: 

for (int k = left; ++left <= right; k = ++left) {

        //Очередную пару рядом стоя?щих элементов 
        //заносим в пару буферных переменных
        int a1 = a[k], a2 = a[left];
        if (a1 < a2) {
                a2 = a1; a1 = a[left];
        }

        //Вставляем больший элемент из пары
        while (a1 < a[--k]) {
                a[k + 2] = a[k];
        }
        a[++k + 1] = a1;
        
        //Вставляем меньший элемент из пары
        while (a2 < a[--k]) {
                a[k + 1] = a[k];
        }
        a[k + 1] = a2;
}

//Граничный случай, если в массиве нечётное количество элементов
//Для последнего элемента применяем сортировку простыми вставками
int last = a[right];
while (last < a[--right]) {
        a[right + 1] = a[right];
}
a[right + 1] = last;


Сортировка Шелла




В этом алгоритме очень остроумный подход в определении того, какую именно часть массива считать отсортированной. В простых вставках все просто: от текущего элемента всё что слева — уже отсортировано, всё что справа — ещё не отсортировано. В отличие от простых вставок сортировка Шелла не пытается слева от элемента сразу формировать строго отсортированную часть массива. Она создаёт слева от элемента почти отсортированную часть массива и делает это достаточно быстро.

Сортировка Шелла закидывает текущий элемент в буфер и сравнивает его с левой частью массива. Если находит бо?льшие элементы слева, то сдвигает их вправо, освобождая место для вставки. Но при этом берёт не всю левую часть, а только некоторую группу элементов из неё, где элементы разнесены друг от друга на некоторое расстояние. Такая система позволяет быстро вставлять элементы примерно в ту область массива, где они должны находиться.

С каждой итерацией основного цикла это расстояние постепенно уменьшается и когда оно становится равным единице, то сортировка Шелла в этот момент превращается в классическую сортировку простыми вставками, которой дали на обработку почти отсортированный массив. А почти отсортированный массив сортировка вставками в полностью отсортированный преобразует быстро.

def shell(data):
    inc = len(data) // 2
    while inc:
        for i, el in enumerate(data):
            while i >= inc and data[i - inc] > el:
                data[i] = data[i - inc]
                i -= inc
            data[i] = el
        inc = 1 if inc == 2 else int(inc * 5.0 / 11)
    return data


Сортировка расчёской по похожему принципу улучшает пузырьковую сортировку, благодаря чему временна?я сложность алгоритма с O(n2) подскакивает аж до O(n log n). Увы, но Шеллу этот подвиг повторить не удаётся — лучшая временна?я сложность достигает O(n log2 n).

Про сортировку Шелла написано несколько хабрастатей, поэтому не будем перегружаться информацией и двигаемся дальше.

Сортировка деревом




Сортировка деревом за счёт дополнительной памяти быстро решает вопрос с добавлением очередного элемента в отсортированную часть массива. Причём в роли отсортированной части массива выступает бинарное дерево. Дерево формируется буквально на лету при переборе элементов.

Элемент сравнивается сначала с корнем, а потом и с более вложенными узлами по принципу: если элемент меньше чем узел — то спускаемся по левой ветке, если не меньше — то по правой. Построенное по такому правилу дерево затем можно легко обойти так, чтобы двигаться от узлов с меньшими значениями к узлам с большими значениями (и таким образом получить все элементы в возрастающем порядке).

Основная загвоздка сортировок вставками (затраты на вставку элемента на своё место в отсортированной части массива) здесь решена, построение происходит вполне оперативно. Во всяком случае для освобождения точки вставки не нужно медленно передвигать караваны элементов как в предыдущих алгоритмах. Казалось бы, вот она, наилучшая из сортировок вставками. Но есть проблема.

Когда получается красивая симметричная ёлочка (так называемое идеально сбалансированное дерево) как в анимации тремя абзацами выше, то вставка происходит быстро, поскольку дерево в этом случае имеет минимально возможную вложенность уровней. Но сбалансированная (или хотя бы близкая к таковой) структура из рандомного массива получается редко. И дерево, скорее всего, будет неидеальное и несбалансированное — с перекосами, заваленным горизонтом и избыточным количеством уровней.

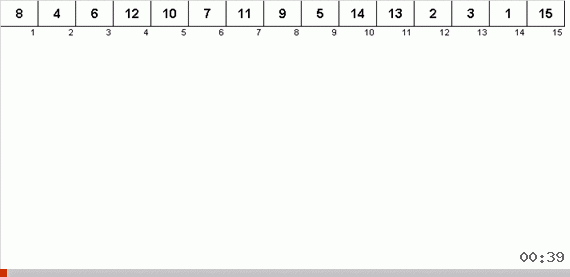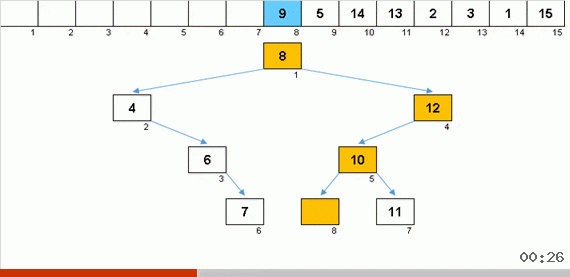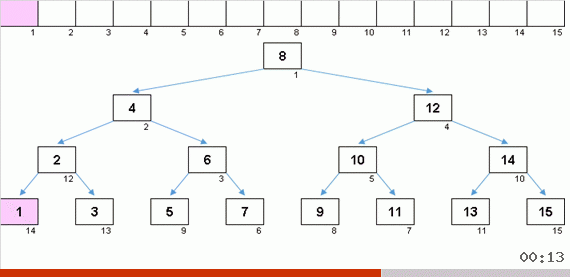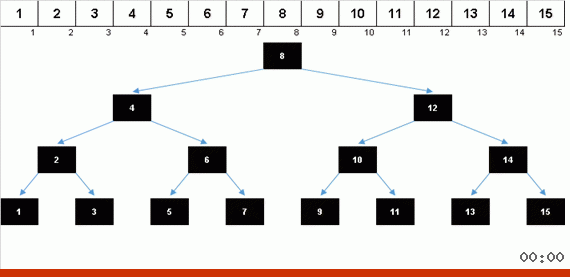
Рандомный массив со значениями от 1 до 10. Элементы в таком порядке генерируют несбалансированное двоичное дерево:



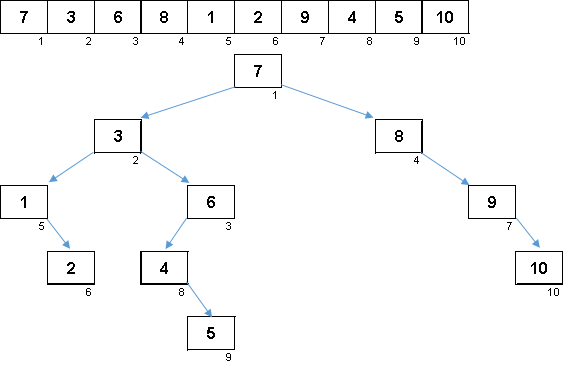
Дерево мало построить, его ещё нужно обойти. Чем больше несбалансированности — тем сильнее будет буксовать алгоритм по обходу дерева. Тут как скажут звёзды, рандомный массив может породить как уродливую корягу (что более вероятно) так и древовидный фрактал.

Значения элементов те же, но порядок другой. Генерируется сбалансированное двоичное дерево:



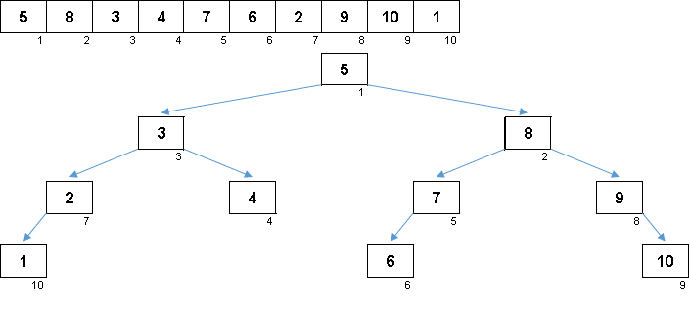
На прекрасной сакуре
Не хватает лепестка:
Бинарное дерево из десятки.

Проблему несбалансированных деревьев решает сортировка выворачиванием, которая использует особую разновидность бинарного дерева поиска — splay tree. Это замечательное древо-трансформер, которое после каждой операции перестраивается в сбалансированное состояние. Про это будет отдельная статья. К тому времени подготовлю и реализации на Python как для Tree Sort, так и для Splay sort.

Ну чтож, мы кратенько прошлись по самым популярным сортировкам вставками. Простые вставки, Шелл и двоичное дерево мы все знаем ещё со школы. А теперь рассмотрим других представителей этого класса, не столь широко известных.

Вики / Wiki — Вставки / Insertion, Шелл / Shell, Дерево / Tree

Статьи серии:



Кто пользуется AlgoLab — рекомендую обновить файл. Я добавил в это приложение простые вставки с бинарным поиском и па?рные вставки. Также полностью переписал визуализацию для Шелла (в предыдущей версии там было не пойми что) и добавил подсветку родительской ветки при вставке элемента в бинарное дерево.

Комментарии (14)


  1. netch80
    02.07.2018 19:44
    #18838179

    Совершенно непонятна причина утверждения, что сортировка расчёской (comb sort) лучше сортировки Шелла (Shell sort). Вики говорит обратное: для Shell sort есть последовательность с O(n log?n), а для comb sort — нет.
    И это логично, если учитывать, что у них два отличия — обмены вместо вставок (обменами — дороже) и отсутствие грамотно подобранной последовательности шагов у comb sort. Если для comb sort вместо обменов применить вставки, получится плохой Shell sort с возможностью до O(n?), а если изменить последовательность gap?ов на любую правильную от Shell sort, получится просто вариант Shell sort чуть дороже, ибо на обменах.
    У вас же Shell sort применена в самом тупом варианте, который устарел полностью.


    1. valemak Автор
      02.07.2018 20:33
      #18838269

      Вызываю Вас на дуэль.

      Вы выставляете лучшую реализацию Shell sort (желательно на Python, но можем обсудить язык). Я со своей стороны подберу реализацию Comb sort. Проверим, кто окажется быстрее.


      1. netch80
        03.07.2018 08:18
        #18839443

        Не принимаю: вы уходите от конкретной темы и при этом пытаетесь брать на «слабо».
        Покажите тот случай, для которого comb sort по данным, по которым сформированы статьи википедии, имеет O(n?), и что вы его обошли, достигнув хотя бы сравнимого O(n log?n). Тогда это будет предметный разговор именно на ту тему, что я поднял.


        1. valemak Автор
          03.07.2018 10:03
          #18839787

          Давайте снова внимательно почитаем Википедию.

          Сортировка расчёской

          Лучшее время — O(n log n)
          Сравнение алгоритма с quick sort (цитата) — "… конкурирует с алгоритмами, подобными быстрой сортировке ..."

          Сортировка Шелла

          Лучшее время — O(n log2 n) — ввиду квадратичности это худший, показатель чем у Comb sort.
          Сравнение алгоритма с quick sort (цитата) — "… Невзирая на то, что сортировка Шелла во многих случаях медленнее, чем быстрая сортировка ...".

          То есть, сама Википедия указывает, что у Comb sort более скоростные показатели чем у Shell sort.

          Что касается «покажите тот случай», то я готов Вам всё показать, просто дайте мне наилучшую по Вашему мнению реализацию Shell sort на том языке программирования, который сочтёте нужным. Я проведу тесты и пришлю Вам все итоговые материалы.


          1. netch80
            03.07.2018 10:28
            #18839905

            > Давайте снова внимательно почитаем Википедию.

            Давайте. Только вы или это не сделали, или невнимательно читали, что я писал. Речь про худший случай, для которого утверждается квадратичная зависимость.

            > То есть, сама Википедия указывает, что у Comb sort более скоростные показатели чем у Shell sort.

            Лучший случай меня _пока_ тут не интересует. Интересует худший, как его детектировать и обходить.
            Например, для quick sort это сделано более 30 лет назад — и формальное определение, и детект, и методы обхода. А тут как?
            Если худший случай невозможно адекватно отлавливать, то сортировка неприменима в случаях, где можно устроить DoS по скорости соответствующим подбором данных (ситуация, реально известная с quick sort с простейшими методами выбора разделяющего элемента).
            А таких случаев всё больше и больше.

            > то я готов Вам всё показать, просто дайте мне наилучшую по Вашему мнению реализацию Shell sort на том языке программирования

            Никакая — ни лучшая, ни обычная — реализация Shell sort не имеет отношения к O(n?) в худшем случае comb sort. Вы уводите разговор в сторону.

            После того, когда (если) этот случай будет отловлен и нейтрализован, можно будет сравнивать скорость на типовых применениях.


            1. valemak Автор
              03.07.2018 10:57
              #18840033

              Сложности в худшем случае (по данным той же Википедии) у этих алгоритмов одинаковы — O(n2). Причём, подозреваю, что вырожденные случаи у Comb sort и Shell sort совершенно разные. На каких-то наборах данных один алгоритм будет зависать, а второй щёлкать как орешки. А универсальных вырожденных случаев (чтобы были одновременно вырожденными для обоих алгоритмов) может запросто и не оказаться. А если так, то какой смысл сравнения по худшему случаю?

              В целом Вы подняли интересную тему. К сожалению, у меня сейчас банально нет времени проводить обстоятельное научное исследование, по отлавливанию и нейтрализации худших случаев для Shell sort / Comb sort. Если Вас так волнует эта тема, то почему бы Вам этим и не заняться за счёт своего, а не моего времени? Я сейчас пишу серию из около 30-ти обзорных (подчёркиваю — обзорных, а не уровня Arxiv.org) статей по 80+ алгоритмам, принадлежащим к 6 основным классам сортировок. Я не буду бросать эту работу только для того, чтобы Вам что-то доказывать по поводу Шелла и расчёски. Так что прошу меня извинить.


              1. netch80
                03.07.2018 13:53
                #18840977
                +1

                > Сложности в худшем случае (по данным той же Википедии) у этих алгоритмов одинаковы — O(n2).

                Нет. Например, у Шелла на 3-smooth numbers гарантируется ?(N(log N)^2).

                > А если так, то какой смысл сравнения по худшему случаю?

                Затем, что в худший случай пусть и сложно попасть без намерения, но с намерением — можно натворить дел.

                > Так что прошу меня извинить.

                Обзорность допускает упрощение, но не искажение, а именно так следует оценивать утверждения вида «сортировке расчёской — удалось преодолеть барьер O(n?) и выйти по времени на заслуживающие уважение O(n log n)», или «У неё нет рекурсии и поэтому в отличие от своих коллег она успешно обработывает массивы, состоящие из миллионов элементов».
                Можете игнорировать, но не удивляйтесь потом оценкам результатов.


                1. valemak Автор
                  03.07.2018 14:34
                  #18841227

                  Есть подозрение, что я двусмысленно выразился в статье и мы вообще говорим о разных вещах.

                  Сортировка расчёской по похожему принципу улучшает пузырьковую сортировку, благодаря чему временна?я сложность алгоритма с O(n2) подскакивает аж до O(n log n). Увы, но Шеллу этот подвиг повторить не удаётся — лучшая временна?я сложность достигает O(n log2 n).
                  Я имел ввиду, что если модифицировать сортировку пузырьком (имеющую сложность O(n2)) в сортировку расчёской, то получаем алгоритм со сложностью O(n log n).
                  А вот если похожей модификацией сортировку вставками (имеющую сложность O(n2)) преобразовать в сортировку Шелла, то получаем алгоритм со сложностью O(n log2 n).
                  То есть и сортировка Шелла и сортировка расчёской — это аналогичные модификации из более простых алгоритмов со сложностью O(n2). И хоть это и похожие модификации, сортировка расчёской всё-таки в общем случае достигает лучших результатов, чем Шелл.

                  Когда я упомянул сложность O(n2) то речь шла о сортировке пузырьком и сортировке вставками. А не о худшей сложности расчёски и Шелла, о чём мы и ведём эту странную дискуссию.


                1. valemak Автор
                  03.07.2018 14:41
                  #18841259

                  Что касается вот этого:

                  У неё нет рекурсии и поэтому в отличие от своих коллег она успешно обработывает массивы, состоящие из миллионов элементов
                  У меня при тестировании действительно различные варианты быстрой сортировки не могут осилить массивы, состоящие из миллионов элементов. А вот расчёска сортирует быстро и без проблем.


                  1. netch80
                    03.07.2018 15:50
                    #18841667
                    +1

                    > У меня при тестировании действительно различные варианты быстрой сортировки не могут осилить массивы, состоящие из миллионов элементов.

                    Хм… интересно, _как_ так надо было писать. Потому что осиливает. На Питоне, конечно, времена будут чудовищные (у меня на 10000 элементов — единицы секунд, а на 10 миллионов это будет два часа пахать), и вообще там больше память сожрёт и всех в своп загонит, но на C++ проблем никаких.

                    Вот моя версия тестов — простая, прямая, но работающая. Можете сравнить со своим quicksort.

                    ptest
                    #!/usr/bin/env python3

import time, random, os, math

shell_gaps = []


def shell_generate_gaps():
    global shell_gaps
    max_gap = int(os.environ.get("ALEN", "1000"))
    c3 = 1
    while c3 <= max_gap:
        c32 = c3
        while c32 <= max_gap:
            shell_gaps.append(c32)
            #- print("__: appended {}".format(c32))
            c32 *= 2
        c3 *= 3
    shell_gaps.sort(reverse = True)


def shell_sort(arr):
    n = len(arr)
    #- gaps = generate_gaps(n)
    for gap in shell_gaps:
        #print("__: gap={}".format(gap))
        #print("__: arr={}".format(arr))
        for i in range(gap, n):
            temp = arr[i]
            j = i
            while j >= gap and arr[j-gap] > temp:
                arr[j] = arr[j-gap]
                j -= gap
            arr[j] = temp
    #print("__: final: arr={}".format(arr))


def comb_sort(arr):
    coeff = 0.8017118471377938
    n = len(arr)
    gap = n
    while True:
        if gap > 1:
            gap = int(gap*coeff)
        #- print("__: comb_sort: run for gap={}".format(gap))
        is_sorted = True
        for i in range(0, n - gap):
            if arr[i] > arr[i+gap]:
                temp = arr[i]
                arr[i] = arr[i+gap]
                arr[i+gap] = temp
                is_sorted = False
        if gap == 1 and is_sorted:
            break


def rec_qsort(arr, li, ri):
    while True: ## instead of recursion
        if ri <= li:
            return
        if ri - li < 10:
            for i in range(li+1, ri+1):
                temp = arr[i]
                j = i
                while j >= li+1 and arr[j-1] > temp:
                    arr[j] = arr[j-1]
                    j -= 1
                arr[j] = temp
            return
        si = random.randint(li, ri)
        temp = arr[li]
        arr[li] = arr[si]
        arr[si] = temp
        lp = li
        rp = ri
        leading_lp = True
        while lp < rp:
            cv = arr[lp] - arr[rp]
            if cv > 0:
                temp = arr[lp]
                arr[lp] = arr[rp]
                arr[rp] = temp
            if cv >= 0:
                leading_lp = not leading_lp
            if leading_lp:
                rp -= 1
            else:
                lp += 1
        if lp != rp:
            raise AssertionError('lp == rp')
        lwx = lp - li
        rwx = ri - rp
        if lwx > rwx:
            rec_qsort(arr, rp+1, ri)
            ri = lp - 1
        else:
            rec_qsort(arr, li, lp-1)
            li = rp+1


def qsort(arr):
    rec_qsort(arr, 0, len(arr) - 1)


def embedded_sort(arr):
    arr.sort()


def generate_array():
    arr_len = int(os.environ.get("ALEN", "1000"))
    akind = os.environ.get("AKIND", "almost_sorted")
    if akind == 'sorted':
        return [i for i in range(arr_len)]
    elif akind == 'reverse':
        return [arr_len-i for i in range(arr_len)]
    elif akind == 'almost_sorted':
        arr = []
        psize = min(int(math.sqrt(arr_len)), 1)
        while len(arr) < arr_len:
            psize1 = min(psize, arr_len - len(arr))
            curr_len = len(arr)
            portion = [i+curr_len+1 for i in range(psize1)]
            random.shuffle(portion)
            arr.extend(portion)
        return arr
    else:
        arr = [i for i in range(arr_len)]
        random.shuffle(arr)
        return arr


def run(sort_func):
    tsum = 0
    for arr in g_arrays:
        arrx = arr[:]
        t0 = time.time()
        sort_func(arrx)
        tsum += time.time() - t0
        for j in range(len(arrx) - 1):
            if arrx[j] > arrx[j+1]:
                print("__: unsorted: j={} a1={} a2={}".format(j, arr[j], arr[j+1]))
                raise RuntimeError("assertion: not sorted")
    return tsum


if __name__ == "__main__":
    shell_generate_gaps()
    g_arrays = [generate_array() for i in range(100)]
    print("shell_sort tsum:", run(shell_sort))
    print("comb_sort tsum:", run(comb_sort))
    print("qsort tsum:", run(qsort))
    print("embedded_sort tsum:", run(embedded_sort))


                    параметры регулирую через окружение (если у вас Windows, возможно, проще поменять умолчания в коде)


                    1. valemak Автор
                      03.07.2018 16:03
                      #18841735

                      А вот тут большое Вам спасибо. На досуге протестирую и даже, скорее всего, возьму эти реализации себе как основные для данных сортировок.

                      А то в комментариях мода такая — пишут: «у вас реализации неэффективные», но хоть бы кто привёл «правильные» варианты алгоритмов.


                      1. netch80
                        03.07.2018 18:14
                        #18842525
                        +1

                        Ну, я не обещаю заметной эффективности этих своих реализаций (например, в C++ моя версия quick_sort, 1:1 переведенная с этого питоновского кода, ест почти в 2 раза больше времени, чем std::sort из рантайма GCC5). Просто работающая версия quick_sort с полной обвязкой.


  1. Prototik
    03.07.2018 08:31
    #18839481
    +1

    Для tree sort я бы ещё добавил вырожденный случай с отсортированным (или почти отсортированным) массивом, когда дерево выстраивается в «лесенку».


    1. valemak Автор
      03.07.2018 09:51
      #18839737

      Я просто в этой статье галопом по Европам прошёлся по общеизвестным вставочным сортировкам, не хотел перегружать и так большой материал вырожденными случаями.

      Через несколько статей будет рассказ про сортировку с помощью splay tree, которая как раз преодолевает вырожденные случаи, возникающие у простого binary tree. Там как раз всё и покажу.