«Цель этого курса — подготовить вас к вашему техническому будущему.»

Привет, Хабр. Помните офигенную статью «Вы и ваша работа» (+219, 2442 в закладки, 394k прочтений)?

Так вот у Хэмминга (да, да, самоконтролирующиеся и самокорректирующиеся коды Хэмминга) есть целая книга, написанная по мотивам его лекций. Мы ее переводим, ведь мужик дело говорит.

Это книга не просто про ИТ, это книга про стиль мышления невероятно крутых людей. «Это не просто заряд положительного мышления; в ней описаны условия, которые увеличивают шансы сделать великую работу.»

Мы уже перевели 28 (из 30) глав. И ведем работу над изданием «в бумаге».

Теория кодирования — I

Рассмотрев компьютеры и принцип их работы, сейчас мы будем рассматривать вопрос представления информации: как компьютеры представляют информацию, которую мы хотим обработать. Значение любого символа может зависит от способа его обработки, у машины нет никакого определенного смысла у используемого бита. При обсуждении истории программного обеспечения 4 главе мы рассматривали некоторый синтетический язык программирования, в нём код инструкции останова совпадал с кодом других инструкций. Такая ситуация типична для большинства языков, смысл инструкции определяется соответствующей программой.

Для упрощения проблемы представления информации рассмотрим проблему передачи информации от точки к точке. Этот вопрос связан с вопросом сохранения информация. Проблемы передачи информации во времени и в пространстве идентичны. На рисунке 10.1 представлена стандартная модель передачи информации.



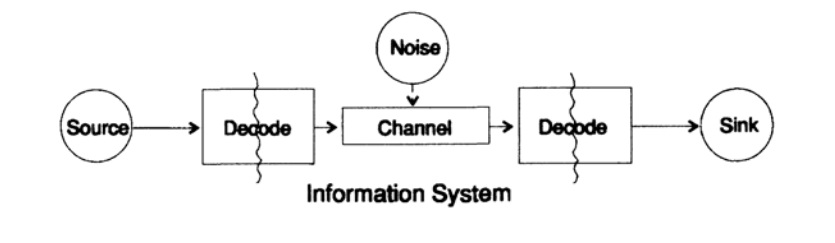
Рисунок 10.1

Слева на рисунке 10.1 находится источник информации. При рассмотрении модели нам неважна природа источника. Это может быть набор символов алфавита, чисел, математических формул, музыкальных нот, символов, которыми мы можем представить танцевальные движения — природа источника и значение хранящихся в нём символов не является частью модели передачи. Мы рассматриваем только источник информации, с таким ограничением получается мощная, общая теория, которую можно распространить на многие области. Она является абстракцией из многих приложений.

Когда в конце 1940 годов Шеннон создал теорию информации, считалось, что она должна была называться теорией связи, но он настоял на термине информация. Этот термин стал постоянной причиной как повышенного интереса, так и постоянных разочарований в теории. Следователи хотели строить целые «теории информации», они вырождались в теории о наборе символов. Возвращаясь к модели передачи, у нас есть источник данных, которые необходимо закодировать для передачи.

Кодер состоит из двух частей, первая часть называется кодер источника, точное название зависит от типа источника. Источникам разных типов данных соответствуют разные типы кодеров.

Вторая часть процесса кодирования называется кодирование канала и зависит от вида канала для передачи данных. Таким образом, вторая часть процесса кодирования согласована с типом канала передачи. Таким образом, при использовании стандартных интерфейсов данные из источника в начале кодируются согласно требованиям интерфейса, а потом согласно требованиям используемого канала передачи данных.

Согласно модели, на рисунке 10.1 канал передачи данных подвергается воздействию «дополнительного случайного шума». Весь шум в системе объединен в этой точке. Предполагается, что кодер принимает все символы без искажений, а декодер выполняет свою функцию без ошибок. Это некоторая идеализация, но для многих практических целей она близка к реальности.

Фаза декодирования также состоит из двух этапов: канал — стандарт, стандарт- приемник данных. В конце передачи данных передаются потребителю. И снова мы не рассматриваем вопрос, как потребитель трактует эти данные.

Как было отмечено ранее, система передачи данных, например, телефонных сообщений, радио, ТВ программ, представляет данные в виде набора чисел в регистрах вычислительной машины. Повторю снова, передача в пространстве не отличается от передачи во времени или сохранения информации. Есть ли у вас есть информация, которая потребуется через некоторое время, то ее необходимо закодировать и сохранить на источнике хранения данных. При необходимости информация декодируется. Если система кодирования и декодирования одинаковая, мы передаем данные через канал передачи без изменений.

Фундаментальная разница между представленной теорией и обычной теорией в физике — это предположение об отсутствии шума в источнике и приемнике. На самом деле, ошибки возникают в любом оборудовании. В квантовой механике шум возникает на любых этапах согласно принципу неопределённости, а не в качестве начального условия; в любом случае, понятие шума в теории информации не эквивалентно аналогичному понятию в квантовой механике.
Для определенности будем далее рассматривать бинарную форму представления данных в системе. Другие формы обрабатываются похожим образом, для упрощения не будем их рассматривать.

Начнем рассмотрение систем с закодированными символами переменной длины, как в классическом коде Морзе из точек и тире, в котором часто встречающиеся символы — короткие, а редкие — длинные. Такой подход позволяет достичь высокой эффективности кода, но стоит отметить, что код Морзе — тернарный, а не бинарный, так как в нём присутствует символ пробела между точками и тире. Если все символы в коде одинаковой длины, то такой код называется блочным.

Первое очевидное необходимое свойство кода — возможность однозначно декодировать сообщение при отсутствии шума, по крайней мере, это кажется желаемым свойством, хотя в некоторых ситуациях этим требованием можно пренебречь. Данные из канала передачи для приемника выглядят как поток символов из нулей и единичек.

Будем называть два смежных символа двойным расширением, три смежных символ тройным расширением, и в общем случае если мы пересылаем N символов приемник видит дополнения к базовому коду из N символов. Приемник, не зная значение N, должен разделить поток в транслируемые блоки. Или, другими словами, у приемника должна быть возможность выполнить декомпозицию потока единственным образом для того, чтобы восстановить исходное сообщение.

Рассмотрим алфавит из небольшого числа символов, обычно алфавиты намного больше. Алфавиты языков начинается от 16 до 36 символов, включая символы в верхнем и нижнем регистре, числа знаки, препинания. Например, в таблице ASCII 128 = 2^7 символов.
Рассмотрим специальный код, состоящий из 4 символов s1, s2, s3, s4

s1 = 0; s2 = 00; s3 = 01; s4 = 11.

Как приёмник должен трактовать следующее полученное выражение

0011?

Как s1s1s4 или как s2s4?

Вы не можете однозначно дать ответ на этот вопрос, этот код однозначно нет декодируется, следовательно, он неудовлетворительный. С другой стороны, код

s1 = 0; s2 = 10; s3 = 110; s4 = 111

декодирует сообщение уникальным способом. Возьмем произвольную строку и рассмотрим, как ее будет декодировать приемник. Вам необходимо построить дерево декодирования Согласно форме на рисунке 10.II. Строка

1101000010011011100010100110…

может быть разбита на блоки символов

110, 10, 0, 10, 0, 110, 111, 0, 0, 0, 10, 10, 0, 110,…

согласно следующему правилу построения дерева декодирования:

Если вы находитесь в вершине дерева, то считываете следующий символ. Когда вы достигаете листа дерева, вы преобразовывает последовательность в символ и возвращайтесь назад на старт.

Причина существования такого дерева в том, что ни один символ не является префиксом другого, поэтому вы всегда знаете, когда необходимо вернуться в начало дерево декодирования.

Необходимо обратить внимание на следующее. Во-первых, декодирование строго поточный процесс, при котором каждый бит исследуется только однажды. Во-вторых, в протоколах обычно включаются символы, которые являются маркером окончания процесса декодирования и необходимы для обозначения конца сообщения.

Отказ от использования завершающего символа является частой ошибкой при дизайне кодов. Конечно же можно предусмотреть режим постоянного декодирования, в этом случае завершающая символ не нужен.



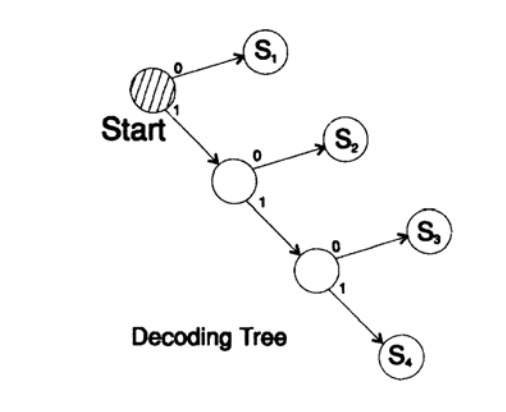
Рисунок 10.II

Следующий вопрос — это коды для поточного (мгновенного) декодирования. Рассмотрим код, который получается из предыдущего отображением символов

s1 = 0; s2 = 01; s3 = 011; s4 = 111.

Предположим мы получили последовательность 011111...111. Единственный способ, которым можно декодировать текст сообщения: группировать биты с конца по 3 в группе и выделять группы с ведущим нулем перед единичками, после этого можно декодировать. Такой код декодируемый единственным способом, но не мгновенным! Для декодирования необходимо дождаться окончания передачи! В практике такой подход нивелирует скорость декодирования (теорема Макмиллана), следовательно, необходимо поискать способы мгновенного декодирования.

Рассмотрим два способа кодирования одного и того же символа, Si:

s1 = 0; s2 = 10; s3 = 110; s4 = 1110, s5 = 1111,

Дерево декодирование этого способа представлено на рисунке 10.III.



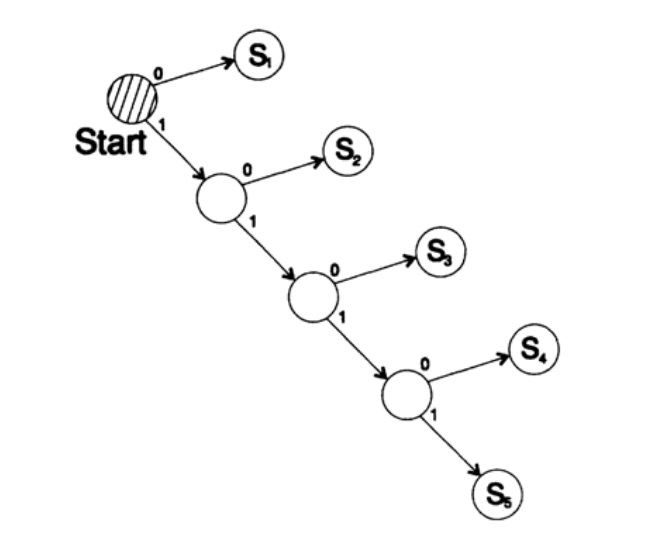
Рисунок 10.III

Второй способ

s1 = 00; s2 = 01; s3 = 100; s4 = 110, s5 = 111,

Дерево декодирование это ухода представлены на рисунке 10.IV.

Наиболее очевидным способом измерения качество кода — это средняя длина для некоторого набора сообщений. Для этого необходимо вычислить длину кода каждого символа, помноженную на соответствующую вероятность появления pi. Таким образом получится длина всего кода. Формула средней длины L кода для алфавита из q символов выглядит следующим образом



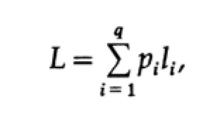
где pi — вероятность появления символа si, li — соответствующая длина закодированного символа. Для эффективного кода значение L должно быть как можно меньше. Если P1 = 1/2, p2 = 1/4, p3 = 1/8, p4 = 1/16 и p5 = 1/16, тогда для кода #1 получаем значение длины кода



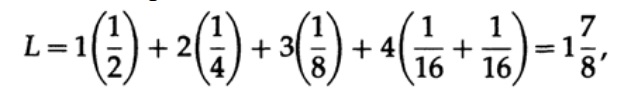
А для кода #2



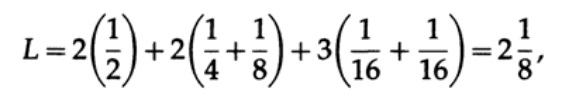
Полученные значения говорят о предпочтительности первого кода.
Если у всех слов в алфавите будет одинаковая вероятность возникновения, тогда более предпочтительным будет второй код. Например, при pi = 1/5 длина кода #1



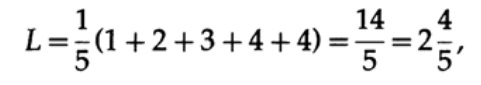
а длина кода #2



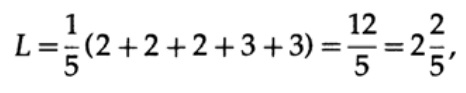
этот результат показывает предпочтительность 2 кода. Таким образом, при разработке «хорошего» кода необходимо учитывать вероятность возникновения символов.



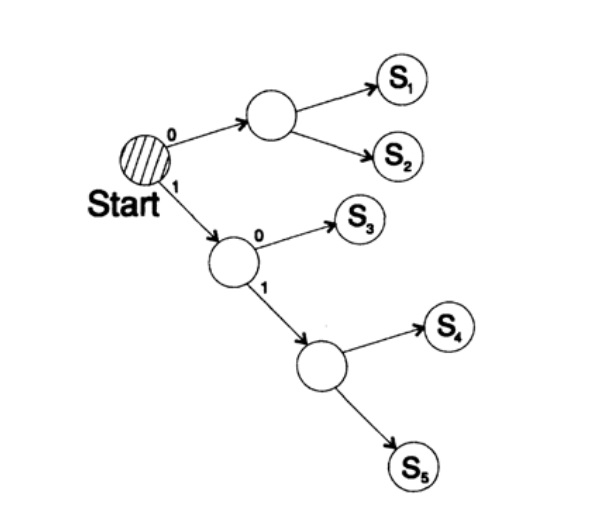
Рисунок 10.IV



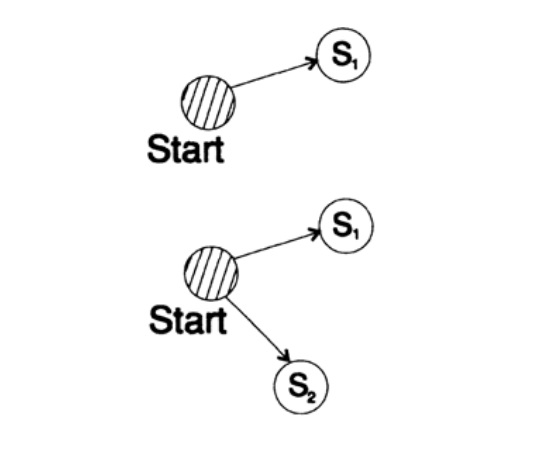
Рисунок 10.V

Рассмотрим неравенство Крафта, которое определяет предельное значение длины кода символа li. По базису 2 неравенство представляется в виде



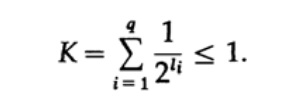
Это неравенство говорит о том, что в алфавите не может быть слишком много коротких символов, в противном случае сумма будет довольно большой.

Для доказательства неравенства Крафта для любого быстрого уникального декодируемого кода построим дерево декодирования и применим метод математической индукции. Если у дерева есть один или два листа, как показано на рисунке 10.V, тогда без сомнения неравенство верно. Далее, в случае если у дерева есть более чем два листа, то разбиваем дерево длинный m на два поддерева. Согласно принципу индукции предполагаем, что неравенство верно для каждой ветви высотой m -1 или меньше. Согласно принципу индукции, применяя неравенство к каждой ветви. Обозначим длины кодов ветвей K' и K''. При объединении двух ветвей дерева длина каждого возрастает на 1, следовательно, длина кода состоит из сумм K’/2 и K’’/2,



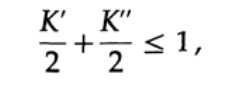
теорема доказана.

Рассмотрим доказательство теорема Макмиллана. Применим неравенство Крафта к непоточно декодируем кодам. Доказательство построено на том факте, что для любого числа K > 1 n-ая степень числа заведомо больше линейной функции от n, где n — довольно большое число. Возведем неравенство Крафта в n-ую степень и представим выражение в виде суммы



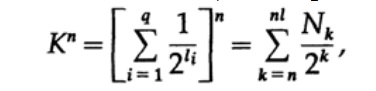
где Nk число символов длины k, суммирование начинаем с минимальной длины n-го представление символа и заканчиваем максимальной длины nl, где l — максимальная длина закодированного символа. Из требования уникального декодирования следует, что. Сумма представляется в виде



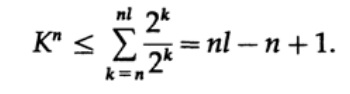
Если K > 1, тогда необходимо n установить довольно большим для того, чтобы неравенство стало ложным. Следовательно, k <= 1; теорема Макмиллана доказана.

Рассмотрим несколько примеров применения неравенство Крафта. Может ли существовать уникально декодируемый код с длинами 1, 3, 3, 3? Да, так как



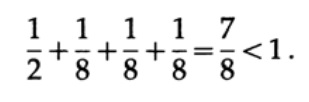
А что насчёт длин 1, 2, 2, 3? Рассчитаем согласно формуле



Неравенство нарушено! В этом коде слишком много коротких символов.

Точечные коды (comma codes) — это коды, которые состоят из символов 1, оканчивающиеся символом 0, за исключением последнего символа, состоящего из всех единичек. Одним из частных случаев служит код

s1 = 0; s2 = 10; s3 = 110; s4 = 1110; s5= 11111.

Для этого кода получаем выражение для неравенства Крафта



В этом случае достигаем равенство. Легко видеть, что для точечных кодов неравенство Крафта вырождается в равенство.

При построении кода необходимо обращать внимание на сумму Крафта. Если сумма Крафта начинает превышать 1, то это сигнал о необходимости включения символа другой длины для уменьшения средней длины кода.

Необходимо отметить, что неравенство Крафта говорит не о том, что этот код уникально декодируемый, а о том, что существует код с символами такой длины, которые уникальна декодируемый. Для построения уникальной декодируемого кода можно присвоить двоичным числом соответствующую длину в битах li. Например, для длин 2, 2, 3, 3, 4, 4, 4, 4 получаем неравенство Крафта



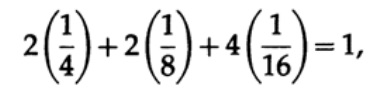
Следовательно, может существовать такой уникальный декодируемый поточной код.

s1 = 00; s2 = 01; s3 = 100; s4 = 101;

s5 = 1100; s6 = 1101; s7 = 1110; s8 = 1111;

Хочу обратить внимание на то, что происходит на самом деле, когда мы обмениваемся идеями. Например, в этот момент времени я хочу передать идею из моей головы в вашу. Я произношу некоторые слова посредством которых, как я считаю, вы сможете понять (получить) эту идею.

Но когда чуть позже вы захотите передать эту идею своему другу, то почти наверняка произнесете совершенно другие слова. В действительности значение или смысл не заключены в рамках каких-то определённых слов. Я использовал одни слова, а вы можете использовать совершенно другие для передачи той же самой идеи. Таким образом, разные слова могут передавать одну и ту же информацию. Но, как только вы скажите своему собеседнику, что не понимаете сообщения, тогда как правило для передачи смысла собеседник подберёт другой набор слов, второй или даже третий. Таким образом, информация не заключена в наборе определенных слов. Как только вы получили те или иные слова, то производите большую работу при трансляции слов в идею, которую хочет до вас донести собеседник.

Мы учимся подбирать слова для того, чтобы подстроиться под собеседника. В некотором смысле мы выбираем слова согласовывая наши мысли и уровень шума в канале, хотя такое сравнение не точно отражает модель, который я использую для представления шумов в процессе декодирования. В больших организациях серьезной проблемой является неспособность собеседника слышать то, что сказано другим человеком. На высоких должностях сотрудники слышать то, «что хотят услышать». В некоторых случаях вам необходимо это помнить, когда вы будете продвигаться по карьерной лестнице. Представление информации в формальном виде является частичным отражением процессов из нашей жизни и нашло широкое применение далеко за границами формальных правил в компьютерных приложениях.

Продолжение следует...

Кто хочет помочь с переводом, версткой и изданием книги — пишите в личку или на почту magisterludi2016@yandex.ru

Кстати, мы еще запустили перевод еще одной крутейшей книги — «The Dream Machine: История компьютерной революции»)